Assisted Software Exploration using Formal

Concept Analysis

Paul Heckmann and Daniel Speicher

Institute of Computer Science III, University of Bonn, Bonn, Germany

Abstract. Program comprehension requires understanding the structures within

the program. Some of these structures are created intentionally and well known

(design pattern), others arise implicitly but are still meaningful, and ﬁnally some

structures emerge accidentally without any meaning. We build on a previously

suggested approach to mine structures in software using Formal Concept Analy-

sis. In contrast to previous work, we found the performance of our tool to be still

acceptable for projects of interesting size (∼600 classes). A prominence index for

classes based on the formal concepts proved to be helpful for the identiﬁcation of

core structures (high prominence) as well for focusing on speciﬁc structures (low

prominence). We report about two experiments. In the ﬁrst the tool guided the

experimenter to central structures of JUnit as documented before but unknown

by the experimenter. In the second the tool led us to the core structures of our

own software.

1 Introduction

An object oriented software system essentially can be seen as a composition of struc-

tural concepts. Concepts in which classes and interfaces are connected with each other

using building mechanisms like abstraction, inheritance, and composition to realize a

certain functionality important to the respective part of the system. Some of these con-

cepts reoccur over the entire project and constitute to a programs unique character,

others reoccur yet only in certain parts suggesting core concepts of the program. Hence

revealing any of these structural concepts can be a ﬁrst important step to understanding

the software itself, its character and its core functionality. But not all of these concepts

arise by design, e.g. by using design patterns as introduced by [6]. They may arise im-

plicitly and strongly depend on the developers style of solving a certain design problem.

In this work we propose an approach to mine structural concepts using a bi-clustering

technique called Formal Concept Analysis (FCA) [7], building on a previous approach

proposed by [11]. This technique allows us to group structures in source code into

meaningful groups without requiring any knowledge on the to-analyze program nor the

existence of a reference library of structures. We then improve this approach by the use

of a more efﬁcient mining algorithm and extend it by adding ﬁltering features that, on

one hand, allows us to interactively and iteratively explore the structures in a program,

and on the other hand supports us in ﬁnding those structural concepts constituting to its

core functionality.

In section 2 we give a brief introduction to the very basic idea of FCA. In section

Heckmann P. and Speicher D..

Assisted Software Exploration using Formal Concept Analysis.

DOI: 10.5220/0004175400110021

In Proceedings of the 3rd International Workshop on Software Knowledge (SKY-2012), pages 11-21

ISBN: 978-989-8565-32-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

3 we reproduce the approach ﬁrstly introduced by [11] to apply FCA on our problem

of mining structures in source code. In section 4 we present our extensions to this ap-

proach. Finally, in section 5 we validate the performance improvement on three software

projects of different size and conduct two experiments to examine the practicability of

our extensions.

2 Formal Concept Analysis

Formal Concept Analysis (FCA) [7][3] is a branch of lattice theory that allows us to

identify meaningful groupings of objects G, i.e. quantities in a data set, that have com-

mon attributes M. In all the extent of this work, we are going to explain FCA on a very

simple yet illustrative example in which we pick a set of birds as G and a set of bird

characteristics as M and organize them in a so called formal context M, as depicted

in Table 1

. This formal context describes an incidence matrix in which M

(i,j)

= 1 if

object i has attribute j.

Table 1. FCA bird example context.

can ﬂy can swim sings migratory monogamous

Ara × ×

Bluejay × × ×

Kiwi ×

Mallard × ×

Pelican × × ×

Using this context, FCA groups the objects and their attributes into formal concepts,

listed in Table 2. Such a formal concept consists of two sets, an extension and an in-

tension. The intension contains all common attributes that apply to the objects in the

extension. In the same way all objects contained in the extension share all properties

contained in the intension. Therefore a concept is a maximal collection of elements

sharing common properties. Adding an attribute to a concept’s intension there would be

at least one object in the extension that does not have this attribute. Adding an object to

the extension there would be at least one attribute in the intension this object does not

have. As a consequence the formal concepts build a complete partial order that can be

written as a lattice. Table 2 in some way suggests this order by the increasing number

objects and the decreasing number attributes from top to bottom.

3 FCA Application

3.1 Setup of the Formal Context

We apply FCA on an object oriented software system by considering structures between

It needs to be noted that ornithology usually is not part of our research. The data shown in

Table 1 may not be entirely correct.

In the context of this particular work, we are not making any use of this partial order.

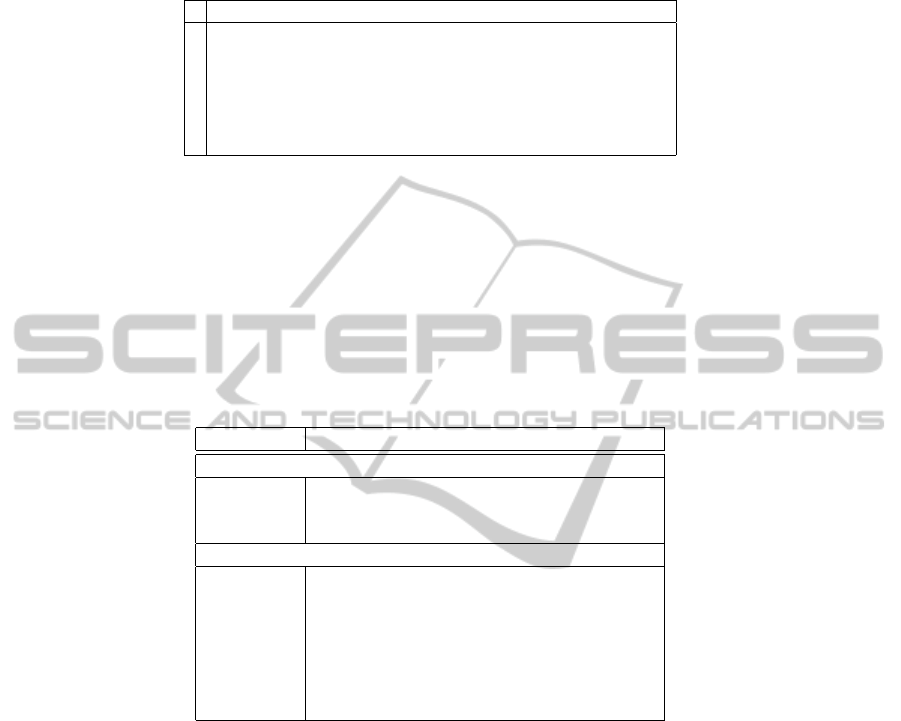
Table 2. Formal concepts for the context in Table 1.

i Extension E

(↓) Intension I

(↑)

{Pelican} {can ﬂy, can swim, migratory}

{Bluejay} {can ﬂy, sings, monogamous}

{Ara, Bluejay} {can ﬂy, monogamous}

{Mallard, Pelican} {can ﬂy, can swim}

{Kiwi, Ara, Bluejay} {monogamous}

{Ara, Bluejay, Mallard, Pelican} {can ﬂy}

classes and interfaces as the set G of FCA objects and class relationships that constitute

to a structure as the set M of FCA attributes. A ﬁrst logical step hence will be to

deﬁne a structure model, i.e. the set of types of relationships we are looking for in a

system. For this, we adapt relationships from LePUS3 [5], a modeling language for

design patterns, and classify them into three structural and four behavioral relationship

types, as listed in Table 3. All relationships are orthogonal to each other. For instance,

the calls relationship between two classes A and B only applies if there is no forwards

relationship between A and B.

Table 3. Our set of relationships used to describe structures in source code.

Relationship r A class A is related to a class/interface B by r if

structural

has A has a one-to-one object association to B.

aggregates A has a one-to-many object association to B.

specializes A extends or implements B.

behavioral

calls a method in A calls a method in B.

forwards a method in A calls a method in B that shares

the same signature.

creates a method in A calls the constructor of a class and

binds the new instance to a variable of type B.

produces a non-private method in A creates a new instance

of B and returns it.

Using this model to describe structures, we then adopt the FCA approach introduced

by [11] and later improved by [1]. Here, having as input the set P of all classes in a

software and a ﬁxed order n ∈ N we gather those class substructures that contain n

classes. Such a substructure can be described by two components, namely its n-tuple

of classes in P

(our FCA object) and a set of relationships between these classes (our

FCA attribute). We illustrate this approach by the example structure in Figure 1 with

P = {A, B, C, D, E} and n = 3. The corresponding formal context to Figure 1 is

shown in Table 4 while Table 5 lists the resulting formal concepts.

3.2 Iterative Concept Analysis

FCA generally is expensive. Its runtime increases exponentially by the set of objects,

the set of attributes and the density of the formal context. In order to reduce the set of

B C

Fig. 1. A simple class structure that could be an input to our FCA approach. It contains ﬁve classes

related to each other by two of our relationship types, has (simple association, diamond at source)

and speciﬁcation (inheritance, triangle at target).

Table 4. Formal context for the structure in Figure 1 and n = 3. Four connected substructures

can be found. The attributes represent relationships and refer to the classes in the tuples by their

indexes. For instance, the attribute spec(2, 1) can be read as ”the element at index 2 specializes

the element at index 1”.

spec(2, 1) spec(3, 1) has(3, 1) has(2, 1) spec(3, 2) has(3, 2) has(1, 3) has(1, 2)

(A, B, C) × × ×

(A, B, D) × × ×

(A, C, D) × × × ×

(A, D, E) × × × ×

concepts computed by FCA as well as its expected runtime, we apply FCA iteratively.

In the ﬁrst iteration, only the three structural relationships in Table 3 are considered,

creating concepts revealing the deﬁnition of a system part. In case we want to further

examine such a deﬁnition in its behavior, we apply FCA only on this part a second

time also considering our behavioral relationships but vastly reducing the set of FCA

objects.

3.3 Postprocessing

Removing Disconnected Structures. Due to the way we construct the formal context

basically two post-processing steps have to be taken. The ﬁrst one is to remove concepts

whose intension describe a disconnected graph. In Table 5 concept c

represents such

a graph, as the nodes with the indexes 1 and 2 are connected with each other, the node

with index 3 is not connected to any of the other two.

Merging Equivalent Structures. For a context like ours FCA may produce concepts

that are basically equivalent and can be merged. That is the case if there exists a per-

mutation of the indexes of two concepts such that the intension of one concept can be

mapped into the other. For instance, in Table 5 concept c

is equivalent to c

by the

mapping 1 → 3, 2 → 1 and 3 → 2. To ﬁnd such a mapping is a graph matching prob-

lem and hence not trivial. We used the VF2 algorithm proposed by [4] to accomplish

this task, however, since the graphs we are trying to match are relatively small a naive

depth-ﬁrst search would work just as well.

The idea was already proposed by [11], with the difference that they used as attribute augmen-

tation the methods calling each other and their names.

Table 5. Formal concepts for the context in Table 4.

i Extension E

(↓) Intension I

(↑)

{(A, D, E)} {has(1, 2), has(3, 2), spec(3, 2), has(2, 1)}

{(A, C, D)} {has(3, 1), has(2, 1), spec(2, 1), has(1, 3)}

{(A, B, C)} {spec(3, 1), has(3, 1), spec(2, 1)}

{(A, B, D), (A, C, D)} {has(1, 3), has(3, 1), spec(2, 1)}

{(A, D, E), (A, C, D)} {has(1, 2)}

{(A, B, D), (A, C, D), (A, B, C)} {spec(2, 1), has(3, 1)}

Removing Redundant Information. As an additional step we remove those concepts

that contain redundant information. This is the case if the structure the concept describes

contains a symmetric subgraph. A prominent example is the ”star pattern” as depicted

in Figure 2 (a). Here we can reduce the pattern to the one in Figure 2 (b) without losing

any information. Since the reduced concepts represent structures of a lower order, we

can ignore them.

B, C

(a) (b)

Extension:

(A, B, C)

Extension:

(A, B), (A, C)

Fig. 2. A ”star pattern” containing redundant information (a) and its reduction (b).

4 Filtering Features

4.1 Corner Elements

In order to dynamically change the space FCA is applied on we deﬁne the term Corner

Element. When gathering all substructures of given order in the setup of the formal

context we proceed inductively, i.e. ﬁrst compute all structures of order n = 2, then

augment them to structures of order n = 3, etc.. Before starting an analysis run we can

declare classes as corner elements and aggregate them in a list. It is then guaranteed that

in the ﬁrst inductive step each structure of order n = 2 consists of at least one element

from the corner element list. As a consequence, the structures serving as FCA objects

then are the union of all structures that evolve around the classes in our list of corner

elements.

4.2 Class Prominence

Taking a look at the extension of a formal concept we gain interesting information on

single classes. One of such is the prominence of a class. For the extension E

⊂ P

a formal concept c we can consider an index r ∈ {1, . . . , n} of the n-tuples in E

as a

role of concept c. A class p ∈ P in any of the n-tuples in G

at the index r then can be

seen as a role player of role r. The set of all role players for a role r in a concept c we

further refer to as P

c,r

. In Table 5, concept c

, we have three roles

according to their

indexes in the 3-tuples, played by the following classes: P

= {A}, P

= {B, C},

= {D, C}.

Given a class p ∈ P and a role r in a concept c, we deﬁne its prominence u(p, r, c)

(3) in r simply as the scaled frequency η(p, r, c) (1) (2) of the class playing this role

multiplied by the size of E

η(p, r, c) =

|{e ∈ E

| e

= p}|

(1)

φ(x) = x/(1 − x) (2)

u(p, r, c) = φ(η(p, r, c)) · |E

| (3)

In a ﬁnal step we compute the absolute prominence u(p) (4) of a class p simply by

summing up the prominence values for a class over all roles over all concepts and

normalize the outcome over the absolute prominences of all classes.

u(p) =

c,r

u(p, r, c) (4)

Throughout the concepts listed in Table 5, apparently the class A is more prominent

than any of the other four classes. Pretending that we replace class A with another class

X in concepts c

-c

, class A would still gain the highest prominence value as it is the

only player of role r = 1 in concepts c

-c

, which all have a larger extension.

The prominence of a class can serve us in two ways: First, the more prominent a

class the higher the probability that it plays a role in a core concept of a software project.

One can see the prominence as a gravitation of a class. The higher, the greater is the part

of a software project that is ’attached’ to this class. Second, it could help us determining

appropriate corner elements as ﬁlters. The lower the prominence of a class, the smaller

the expected number computed concepts.

5 Case Studies

5.1 Our Tool

We implemented our approach as part of the Cultivate

plugin for the Eclipse

IDE.

Cultivate is a code analysis tool for Java programs. It in turn bases on the JTransformer

plugin which provides a Prolog factbase that represents the full abstract syntax tree of

the to-analyze Java program. Cultivate implements several program analyses written in

The number roles is determined by the order n.

http://sewiki.iai.uni-bonn.de/research/cultivate/start

http://www.eclipse.org/

http://sewiki.iai.uni-bonn.de/research/jtransformer/start

Prolog that are applied on this factbase.

To compute the formal concepts we use a relatively young algorithm proposed by [9].

This algorithm is particularly suitable to our approach compared to the algorithm [7]

used by previous works because it saves time not carrying the hierarchical order of the

concepts required to build the concept lattice. Due to our post-processing reorganizing

the computed concepts this additional information is useless to us anyway. Secondly,

this algorithm allows us to parallelize the computation, distributing the computational

load over several CPUs.

5.2 Data Set

We apply our tool on three different Java projects:

– JUnit

4.7, which is a testing framework for Java code of smaller size.

– Cultivate, the framework our tool is based on. It consists of a platform providing

utility classes and the engine on one hand and several addons on the other hand

that build upon this platform but not upon each other. As a consequence the overall

cohesion in this project is very low. Also we are familiar with its domain, which

makes it easier to evaluate our ﬁndings.

– JHotDraw

7, a free Java-based framework for creating graphical editors. In con-

trast to Cultivate we are not familiar with this project, yet enjoy it to be well doc-

umented. Also the overall cohesion of the project compared to Cultivate is fairly

high.

For the sake of simplicity we consider only the set of core classes (ignoring external

library classes) that fulﬁll the following requirements: The class neither is of a basic

type (Integer, Double, ...), an enumeration type nor an anonymous class.

5.3 Performance

We ran our analyses on an Intel Quad Core @2.83 GHz with 4 GB RAM under normal

load. Table 6 shows the runtime behavior we observed and number concepts computed

for each of the three sample projects and with regard to the order n. For n ≥ 5 on Cul-

tivate our tool failed due to lack of memory. This may or may not be caused by Prolog

and the fact it loads the entire factbase into the main memory as well as it caches its

Table 6. Observed runtime behavior of our tool in seconds and number concepts computed in the

ﬁrst iteration.

JUnit 4.7 Cultivate JHotDraw 7

#classes 143 607 625

runtime concepts runtime concepts runtime concepts

n = 2 <1s 5 ∼2s 7 ∼3s 9

n = 3 <1s 16 ∼3s 45 ∼14s 38

n = 4 ∼1s 24 187s 154 130s 141

http://www.junit.org

http://sourceforge.net/projects/jhotdraw

query results. The reason why the analysis on JHotDraw is faster than on Cultivate for

n > 3 we ascribe to Cultivate being way less cohesive than JHotDraw, which eventu-

ally leads to a faster growth of concepts in n. Yet the actual number concepts in both

projects are insigniﬁcantly different what suggests a fairly large impact of our addi-

tional post-processing.

Recalling previous observations made by [1], using the Ganter algorithm [7] the analy-

sis of a sample project written in Smalltalk with 167 classes and n = 4 took approx. two

days.

Compared to this, our own results by far excel our expectations and prove this

technique to be a time-efﬁcient way to analyze software projects even of larger scale.

6 Example Applications

6.1 Experiment 1: JUnit

In a ﬁrst experiment we pick the smaller of our sample projects, JUnit, and let one of the

authors apply our tool on it with the goal to yield most relevant structures of the project

in at most ﬁve analysis steps. The project is well-documented and makes extended use

of design patterns, however, the experimenter neither is familiar with the project nor

with its documentation at the time of execution.

As a ﬁrst step, the experimenter runs an analysis on structures of order n = 2. Despite

our expectations we found n = 2 particularly instructive, as its corresponding concepts

are small in number, easy to understand and most often already reveal those atomic

relationships between two classes larger patterns are only based on. The analysis com-

putes ﬁve concepts of which the one depicted in Figure 3 (a) catches the experimenters

attention as it is one of two with more than one relationship. This pattern suggests the

implementation of a tree structure using the Composite pattern [6]. In order to check

this presumption the experimenter runs an analysis on order n = 3 using the class

TestSuite as a corner element. Since this class has a signiﬁcantly smaller promi-

nence than Test, it is more suitable as a ﬁlter. Two concepts are computed, one of

them actually representing the Composite pattern as depicted in Figure 3 (b).

As a speciﬁcation of Test we ﬁnd a class called TestDecorator in Figure 3 (b)

which suggests the implementation of the Decorator pattern [6]. Following the same

procedure as before (using TestDecorator as corner element) we can verify our

presumption.

Rechecking our ﬁndings so far with the JUnit documentation we can verify the com-

posite pattern instance as one most relevant to the base framework, while the decorator

pattern instance is particularly important to the extensional part which can be used by

developers to implement and plug in custom test deﬁnitions.

6.2 Experiment 2: Cultivate

In a second experiment we wanted to examine the precision of the prominence calcula-

tion and how it can be exploited to ﬁnd core concepts in a software project. For this, we

A less advanced hardware may have an impact on these stats, too, considering the previous

observations date back eight years.

Test

TestSuite

TestCase

TestDecorator

JUnit4TestAdapter

JUnit4TestCaseFacade

forwards

Test

TestSuite

forwards

(a)

(b)

Fig. 3. Composite pattern candidate (a) and veriﬁed instance (b) in JUnit 4.7.

use our own project, Cultivate. Firstly, because we are familiar with it and can assess the

validity of the computed prominence values. Secondly, Cultivate basically is a platform

with a few core classes that, however, are extensively used by the add-ons that build on

the platform.

We run an analysis on structures of order n = 3 and retrieve the list of all occur-

ring classes ranked by their prominence. The one with the highest prominence value

is CultivateViewPart (∼12%), the next-prominent class is BaseQuery (∼3%).

In both cases we agree with the tool: CultivateViewPart is a class used as an

abstract view part that follows selections in the workbench and manages the subscrip-

tion of analyses on the corresponding software projects. It is basically inherited from all

add-on projects that provide a workbench view and in fact is one of the central classes

in Cultivate. BaseQuery is the abstract class to query analyses on Prolog side, spe-

cialized by 63 different classes inside the add-on parts.

We declare CultivateViewPart as corner element and run the analysis again. The

result is a set of 14 concepts of which two describe exactly the main responsibilities of

this class, depicted in Figure 4.

CultivateViewPart

ConﬁgurationQueriesModel

Repopsitory

creates

CultivateViewPart

IJavaSelectionListener

JavaSelectionService

(a) (b)

Fig. 4. Two core concepts of the Cultivate project. In Figure (a) the CultivateViewPart

creates and attaches to a ConfigurationQueriesModel object which then retrieves a

Repository for the currently selected project and handles query subscriptions on that repos-

itory. (b) describes an Observer pattern [6], in which CultivateViewPart is an observer,

JavaSelectionService handles workbench selections.

7 Discussion

We can see that FCA is a practical approach to mining structures in software projects

even of larger size. By not only considering the intension of each concept but also its

extension, we ﬁnd a promising approach to assess the relevance and importance of cer-

tain classes of the software project. Having such an assessment we can exploit it either

as a clue to search and identify core concepts of the corresponding project or as an as-

sistance in choosing appropriate ﬁlter elements to narrow down the space the analysis

is applied on.

A very interesting observation we made during our studies on this technique is the im-

portance of structures of order n = 2. They are in many cases atomic components of

structural concepts such as design patterns that represent the core relationship the pat-

tern is based on. For instance, in the ﬁrst experiment we started with the ﬁve structures

of order n = 2 and could easily detect a composite and a decorator pattern (as described

in 6.2) as well as Facade and a Chain Of Responsibility pattern [6].

Yet we think the overall number concepts computed with regard to the order n and

the size of our relationship model is too high to be convenient. On the other hand, reduc-

ing the set of relationships as FCA attributes lead to more abstract concepts, requiring

the user to more often investigate the source code in order to understand the context of

a concept. During our studies on this approach we found ourselves gaining preferences

on patterns over others, suggesting there can be deﬁned heuristics about patterns be-

ing interesting and hence relevant or not. Given such heuristics one can impose further

structural constraints to extend the post-ﬁltering.

8 Related Work

Formal Concept Analysis (FCA) was ﬁrstly proposed by [7] as a branch of lattice the-

ory. The ﬁrst effort towards structure mining in source code using FCA was achieved

by [11]. Their approach then was later reﬁned by [1] who reduced the number FCA

objects and hence improved the overall runtime. Further structure mining efforts for

object-oriented systems have been achieved by [12][8][2] who used subgraph matching

to group same structures formed by classes. We adopted the approach by [11] reﬁned by

[1], enhanced the set of FCA attributes, i.e. class relationships, using a set of relation-

ships based on the modeling language LePUS3 by [5] and exchanged the previously

used algorithm to compute formal concepts by a relatively young algorithm that was

proposed by [9].

A slight connection to our ﬁndings of the importance of order 2 structures can be

drawn to [10], who tried to decompose design patterns into their elemental parts.

References

1. G. Ar

evalo. High Level Views in Object-Oriented Systems using Formal Concept Analysis.

PhD thesis, University of Bern, 2004.

2. A. Belderrar, S. Kpodjedo, Y.-G. Gu

eneuc, G. Antoniol, and P. Galinier. Sub-graph Min-

ing: Identifying Micro-architextures in Evolving Object-oriented Software. Europ. Confer-

ence on Software Maintenance and Reengineering, 2011.

3. C. Carpineto and G. Romano. Concept Data Analysis, Theory and Applications. Wiley &

Sons, 2004.

4. L. P. Cordella, P. Foggia, C. Sansone, and M. Vento. An improved algorithm for matching

large graphs. In In: 3rd IAPR-TC15 Workshop on Graph-based Representations in Pattern

Recognition, Cuen, pages 149–159, 2001.

5. A. H. Eden, Y. Hirshfeld, and A. Yehudai. LePUS - A Declarative Pattern Speciﬁcation

Language. Technical report, 1998.

6. E. Gamma, R. Helm, and R. Johnson. Design Patterns. Elements of Reusable Object-

Oriented Software. Addison-Wesley Longman, 1994.

7. B. Ganter and R. Wille. Formal Concept Analysis: Mathematical Foundations. Springer,

1998.

8. M. Gupta and A. Pande. Design patterns mining using subgraph isomorphism: Relational

view. International Journal of Software Engineering and Its Applications (IJSEIA), 2011.

9. P. Krajca, J. Outrata, and V. Vychodil. Parallel Recursive Algorithm for FCA. In Concept

Lattices and Their Applications (CLA), pages 71–82, 2008.

10. J. M. Smith and D. Stotts. Elemental Design Patterns: A Formal Semantics for Composition

of OO Software Architecture. In IEEE/NASA Software Engineering Workshop, pages 183–

190, 2002.

11. P. Tonella and G. Antoniol. Object Oriented Design Pattern Inference. In Proceedings of

ICSM, page 230ff. IEEE Computer Society Press, 1999.

12. Z.-X. Zhang, Q.-H. Li, and Ke-Rongben. A New Method for Design Pattern Mining. Inter-

national Conference on Machine Learning and Cybernetics, 2004.