Facing the Challenge of Estimating Human Brain

White Matter Pathways

Adelino R. Ferreira da Silva

Dep.

de Eng.

Electrot´ecnica, Faculdade de Ciˆencias e Tecnologia, FCT, Universidade Nova de Lisboa,

2829-516 Caparica, Portugal

Keywords:

High Angular Resolution Diffusion Imaging (HARDI), Fiber Tractography.

Abstract:

Diffusion anisotropy has been used to characterize white matter neuronal pathways in the human brain, and

infer global connectivity in the central nervous system. However, mapping complex ﬁber conﬁgurations in

vivo remains a challenging task. We present a new methodology to reduce uncertainty in estimating the

orientation of neuronal pathways in high angular resolution diffusion imaging (HARDI) reconstructions. The

methodology relies on three main features. First, an optimized HARDI reconstruction technique based on

the generalized q-sampling imaging approach is adopted. Second, directional statistics are used to estimate

orientation distribution function (ODF) proﬁle directions from data distributed on the unit sphere. Third, a

modiﬁed streamline algorithm able to accommodate multiple ﬁber tracts and multiple orientations per voxel is

used, to exploit the directional information gathered from estimated ODF proﬁles. The methodology has been

tested on synthetic data simulations of crossing ﬁbers and on a real data set.

1 INTRODUCTION

Diffusion tensor imaging (DTI) is a widely used

method in clinical research that models the average

diffusion properties of water molecules inside a voxel

based on a Gaussian diffusion assumption. Diffusion

anisotropy, derived by DTI, has been used to char-

acterize white matter neuronal pathways in the hu-

man brain, and infer global connectivity in the cen-

tral nervous system (Basser et al., 2000). White mat-

ter ﬁber tractography is commonly implemented us-

ing the principal diffusion direction of the DTI model

(Mori and van Zijl, 2002). Popular ﬁber tracking ap-

proaches, such as the streamline tracking algorithm,

uses the DTI model to extract the orientation depen-

dence of the diffusion probability density function of

water molecules, and reconstruct the orientation dis-

tribution function (ODF) of anisotropic tissues. How-

ever, the standard single-tensor DTI model is based

on a Gaussian diffusion assumption, thus unable to

resolve crossing and splitting of ﬁber bundles.

High angular resolution diffusion imaging

(HARDI) techniques have been proposed in the liter-

ature to overcome the limitations of the DTI method,

and enable detection of multiple ODF maxima per

voxel (see (Lenglet et al., 2009) for a review). Several

studies have shown that ﬁber tracking based on HAR-

DI-based techniques is improved and less sensitive to

noise errors compared to tensor based tracking (De-

scoteaux et al., 2009), (Polzehl and Tabelow, 2011).

The application of these methods is based on the as-

sumption that the principal directions extracted from

the ODF can be interpreted as principal directions

of the underlying ﬁber architecture. Typically, local

maxima of the reconstructed ODF are located sim-

ply by selecting a large number of randomly sampled

points on the sphere and searching within a ﬁxed ra-

dius neighborhood (Descoteaux et al., 2009). Some

more sophisticated heuristics built on this basic ap-

proach have been proposed. For instance, in (Jian

et al., 2007), a Quasi-Newton method is used to re-

ﬁne the position of each local maximum. However,

as shown in (

Ozarslan et al., 2006) and (Lenglet

et al., 2009), the peaks of the ODF proﬁles identi-

ﬁed by these methods do not necessarily match the

orientations of the distinct ﬁber populations. Since

uncertainty in tractography arises from uncertainty

in estimating the directions of propagation, HARDI

reconstructions can still be ambiguous and difﬁcult

to interpret in the presence of complex ﬁber tract

conﬁgurations. To reduce uncertainty and increase

robustness in HARDI reconstructions, one may in-

crease the number of sampling directions, and use

higher strengths of diffusion-sensitive gradients (b-

709

R. Ferreira da Silva A..

Facing the Challenge of Estimating Human Brain White Matter Pathways.

DOI: 10.5220/0004177207090714

In Proceedings of the 4th International Joint Conference on Computational Intelligence (SSCN-2012), pages 709-714

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

values) to attain satisfactory angular resolution (Cho

et al., 2008). Unfortunately, this solution is imprac-

tical in clinical applications. Increasing the number

of sampling directions prolongs the scan time, mak-

ing HARDI reconstructions susceptible to motion-

induced errors (Jiang et al., 2002). Using high b-

values in clinical scanners results in low signal-to-

noise ratio (SNR) and substantial diffusion-induced

signal decay (Kuo et al., 2008). Poor SNR affects the

accuracy of ODF reconstruction, and increases ﬁber

orientation uncertainty.

In this paper, we present a new methodology to

reduce uncertainty in estimating the orientation of

neuronal pathways in HARDI reconstructions. The

methodology may be summarized in the following

three aspects. First, an optimized HARDI reconstruc-

tion technique based on the generalized q-sampling

imaging (GQI) approach (Yeh et al., 2010) is adopted.

Second, directional statistics are used to estimate

ODF proﬁle directions from data distributed on the

unit sphere. The method focus on clustering data on

the unit sphere, where complexity arises from repre-

senting ODF proﬁles as directional data. Sampling

densities on the hemisphere are used in ODF proﬁle

mapping. Third, a modiﬁed streamline algorithm able

to accommodate multiple ﬁber tracts and multiple ori-

entations per voxel is used to exploit the directional

information gathered from estimated ODF proﬁles.

By combining HARDI reconstruction and directional

statistics in an integrated framework, the methodol-

ogy is expected to support more accurate ﬁber ODF

estimation for white matter ﬁber tractography than

other more traditional approaches. The methodology

has been tested on synthetic data simulations of cross-

ing ﬁbers and on a real data set. The implementation

is integrated in a coherent framework based on the R

language (R Development Core Team, 2010) with 3D

OpenGL visualization capabilities.

2 HARDI RECONSTRUCTIONS

The generalized q-sampling imaging method pro-

posed in (Yeh et al., 2010) is a HARDI approach to

estimate the ODF directly from diffusion MR signals.

The relation between the acquired diffusion weighted

images W(r,q) and the measured ODF ψ

(r,

u) is

given by

(r,

u) = A

∆

∑

W(r,q)sinc(2πL

∆

q·

u), (1)

where r is the voxel coordinate,

u represents a ra-

dial spherical unit direction, q is the wave vector in

q-space, L

∆

is the diffusion sampling length, and A

is a constant area term. The wave vector is given by

q = γδG/2π, where γ is the nuclear gyromagnetic ra-

tio, and G and δ are the strength and duration of the

diffusion-encoding gradient, respectively.

Equation (1) is simple to interpret. The estimated

ODF is synthesized from a series of sinc basis func-

tions, weighted by W(r,q). The shape of the basis

functions is determined by the value of |q|L

∆

. A

higher value of |q|L

∆

represents a sharper contour,

and vice versa. Moreover, (1) speciﬁes an operational

sampling scheme in q-space from which the ODF can

be estimated. In particular, the number of basis func-

tions used in (1) is not restricted by the shell (or grid)

resolution used for MRI signal acquisition. The num-

ber of radial sampling directions can be adapted for

the purposes of ODF estimation. Typically, sampling

densities of N = 81 and N = 321 on the hemisphere

are used in ODF proﬁle mapping, corresponding to

a third and seventh-order tessellation of the icosahe-

dron, respectively. However, this speciﬁcation is not

imposed a priori by the acquisition resolution on the

GQI reconstruction process.

The second main feature of the proposed method-

ology is concerned with multiple directional mapping.

Starting with the raw HARDI signal acquired on a

grid of q-space, the ODF proﬁle is estimated at each

voxel, considering a sampling density of unit vectors

on a unit S2 grid. When a threshold is applied to

the estimated ODF at each voxel, the non-thresholded

unit vectors provide directional statistics information

about the estimated ODF proﬁle. The main ODF ori-

entations at each voxel relevant for ﬁber tracking may

be estimated by clustering the non-thresholded unit

vectors. This directional clustering procedurehas sev-

eral advantages compared to traditional approaches

for orientation mapping. In fact, current best practices

perform multiple maxima extraction based on proce-

dures which are very sensitive to the local modes that

appear in the reconstructed ODFs. Signal noise and

low sampling resolution yield deformed ODF recon-

struction proﬁles, thus affecting accuracyof the multi-

ple orientation determination. In contrast, estimating

orientations from clustered directional data is much

less sensitive to local modes in the reconstructed ODF

proﬁle. Moreover, the procedure is more robust to

noise since it estimates orientations statistically from

sampled data.

For directional clustering estimation, we consider

a mixture of k von Mises-Fisher (vMF) distributions

(Banerjee et al., 2005) that serves as a model for di-

rectional ODF proﬁle data, corresponding to multiple

ﬁber orientations. A mixture of k vMF distributions

has a density given by

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

710

(a)

(b)

Figure 1: (a) Simulated noise free ﬁeld of diffusion proﬁles, reconstructed ﬁeld of ODF glyphs, and estimated ODF directions,

from left-to-right respectively. (b) Simulation as in (a) with Rician noise level SNR=30.

f(x|Θ) =

∑

h=1

(x|θ

), (2)

where f

(x|θ

) denotes a vMF distribution with

parameter θ

= (µ

,κ

) for 1 ≤ h ≤ k, Θ =

{α

,.. ., α

,θ

,.. ., θ

}, and the α

are non-negative

and sum to 1. A d-dimensional unit random vector

x ∈ S

d−1

is said to have d-variate vMF distribution if

its probability density function is given by

(x|µ,κ) = c

(κ)e

κµ

, (3)

where kµk = 1, κ ≥ 0, d ≥ 2, and c

(κ) is a normal-

izing constant (Mardia and Jupp, 2000). The density

(x|µ,κ) is parameterized by the mean direction µ,

and the concentration parameter κ. The κ parameter

characterizes how strongly the unit vectors drawn ac-

cording to f

(x|µ,κ) are concentrated about the mean

direction µ. In this work, we used the procedure for

clustering directional data outlined in (Banerjee et al.,

2005), and implemented in (Hornik and Gr¨un, 2011).

3 EXPERIMENTS

3.1 Simulated Field of Diffusion Proﬁles

To illustrate the methodology described in Section 2,

we generated a ﬁeld of simulated diffusion proﬁles

as depicted in Figure 1. The ﬁeld simulates crossing

ﬁbers with an angle of 60

◦

, and b=4500. Figure 1(a)

illustrates the simulated noise free ﬁeld, the recon-

structed ﬁeld of ODF glyphs using the GQI method,

and the estimated ODF directions based on the vMF

mixture approach. A similar proﬁle simulation with

added Rician noise, and a signal-to-noise (SNR) value

of 30 is shown in Figure 1(b). As illustrated, the vMF

approach correctly identiﬁes the underlying ﬁber ori-

entations in both cases.

3.2 Real Data Experiment

We report on experiments using a DICOM data

set provided by the “Advanced Biomedical MRI

Lab, National Taiwan University Hospital”. Specif-

ically, we have used the data set “DSI 203-point

3mm” which is included in the “DSI Studio” pack-

age, publicly available from the NITRC repository

(http://www.nitrc.org). This data set is from a nor-

mal 24-year-old male volunteer, and has been pro-

vided as a demonstration data set in connection with

the “DSI Studio” software for diffusion MR images

analysis (Yeh et al., 2010). The data set was obtained

with an echo planar imaging diffusion sequence with

twice-refocused echo, dimension 64 × 64 × 40, and

slice thickness 2.9 mm. Further details on the data

set speciﬁcation are available from the NITRC repos-

itory. We have tested our model with the two b-tables

that accompanies the data set. One is a b-table for a

S2-like grid denoted by “dsi203 bmax4000.txt”. The

other is the b-table for the 3D-DSI sampling scheme

used in the DICOM data acquisition. This b-table has

203 points uniformly distributed on a 3D grid limited

to the volume of the unit sphere. In both tables, the

b-values range from 0 to 4000.

Figure 2 shows the views sagittal, coronal and ax-

ial for slices [X,Y,Z] = [22,29,24] of a region of inter-

est (ROI) overlayed on the original data set with non-

brain tissue removed. The ROI image depicts brain

regions where anatomic white matter ﬁber crossings

FacingtheChallengeofEstimatingHumanBrainWhiteMatterPathways

711

Figure 2: Sagittal, coronal and axial views (from left-to-right) for slices [X,Y,Z] = [22,29,24] of the selected ROI volume

overlayed on the original data set with non-brain tissue removed. The sagittal view has the front brain facing right; coronal

and axial views have the right hemisphere on the left of the image (radiological convention).

Figure 3: Linemaps for the ﬁeld of proﬁles estimated from the ODFs, for voxels in axial slices 23 (left), and 24 (right). The

panels also depict the ROI (SLF and CT regions as dark hues) overlayed on the central regions of slices 23 and 24.

are known to exist, forming multiple pathway bun-

dles connected to the cerebral cortex. The ROI was

formed by extracting the superior longitudinal fas-

ciculus (SLF) and corticospinal tract (CT) regions

based on the “ICBM-DTI-81 White-Matter” atlas in-

cluded in the FSL toolbox (Smith et al., 2004). The

extracted regions were registered to the DSI data set

using the FSL/FLIRT tool. Using the procedure out-

lined in Section 2, we estimated for each voxel of the

DSI data set the main ODF directions. This infor-

mation enables us to draw linemaps showing the es-

timated orientations, and number of ﬁbers for each

voxel.

We show in Figure 3 linemaps for the ﬁeld of pro-

ﬁles estimated from the ODFs, for voxels in axial

slices 23 (left), and 24 (right). The selected ROI im-

age is overlayed on Figure 3, in order to pinpoint the

location of the SLF and CT regions on the linemaps.

Figure 3 depicts central regions of slices 23 and 24,

where a large number of voxels with crossing ﬁbers is

clearly visible (see right SLF for slice 23, and left SLF

for slice 24). The central area in Figure 3 is typical of

horizontal ﬁbers associated with the corpus callosum.

Using the estimated voxel directional information,

we implemented a streamline tractographic algorithm

to represent and visualize the ﬁber tracts. The algo-

rithm is a modiﬁed version of the ﬁber tracking al-

gorithm described in (Mori and van Zijl, 2002). The

modiﬁcations were implemented in order to deal with

multiple directional orientations and multiple ﬁber

tracts per voxel. Fiber tracts are initiated in every

voxel within a speciﬁed user deﬁned ROI using one

of the estimated main voxel ODF directions, and are

extended bi-directionally in steps less than half of the

voxel dimension. The tracts are then propagated a

step parallel to the selected direction. For each new

voxel in the path front, one speciﬁc direction among

the estimated voxel ODF directions is selected. The

voxel ODF direction that produces least curvature

with the incoming path is selected for propagation.

Multiple tracts per voxel are accommodated by ini-

tializing the tracts with random real values within the

seed voxel. The number of initializing tracts may be

speciﬁed by the user, enabling him to strike a bal-

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

712

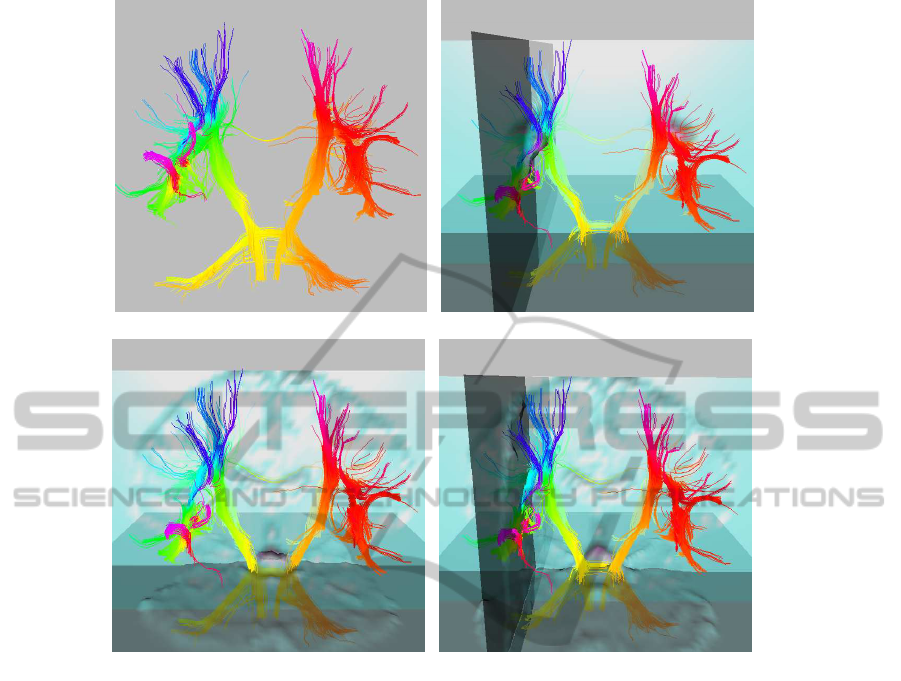
(a) (b)

Figure 4: Panels representing the 3D OpenGL interface used to visualize the estimated ﬁber pattern in the context of the brain

anatomy: (a) Estimated ﬁber pattern using multiple directional orientation and multiple ﬁber tracts per voxel; In (b) ﬁber

tracts are overlayed on image slices of the selected ROI region; In (c) and (d) ﬁber tracts are overlayed on image slices of the

brain.

ance between ﬁber bundle density and running time.

The usual criteria for line keeping and line termina-

tion have been adopted. In particular, the following

criteria have been speciﬁed: minimum ﬁber length

(50 mm), maximum ﬁber length (600 mm), maximum

admissible ﬁber deviation angle(60

), and general-

ized fractional anisotropy threshold (0.2). In Figure 4

we show several panels representing the 3D OpenGL

(Adler and Murdoch, 2010) interface used to visual-

ize the estimated ﬁber pattern in the context of the

brain anatomy. Figure 4(a) illustrates the pattern of

interconnections using the voxels in SLF and CT re-

gions as seeds, and bundles with 10 randomly initial-

ized tracts per voxel. Figure 4(b) maps the ﬁber tracts

overlayed on image slices of the selected ROI region.

Figure 4(c) and Figure 4(d) map the ﬁber tracts over-

layed on image slices of the brain.

4 CONCLUSIONS

We have presented a HARDI reconstruction approach

incorporating directional statistics informationto sup-

port in vivo ﬁber tractography. Based on experiments,

the proposed approach was found to be more accurate

in estimating local ﬁber orientations than traditional

deterministic techniques based on multiple maxima

extraction. Directional accuracy impacts strongly on

the quality of the reconstructed ﬁber maps, and sub-

sequent interpretation of ﬁber tract anatomy for use

in clinical imaging. An extended tractographic pro-

cedure able to accommodate multiple pathways and

bundled ﬁbers was outlined to proﬁt from the richer

directional information gathered at each voxel.

The proposed approach applies statistical infor-

mation criteria to decide on the number of compo-

nents (voxel ﬁbers) to select. The BIC selection cri-

terion used for discriminating between single- and

FacingtheChallengeofEstimatingHumanBrainWhiteMatterPathways

713

crossing-ﬁber voxel conﬁgurations, as well as for es-

timating the number of ﬁbers per voxel, was adequate.

Nevertheless, one drawback of the proposed method-

ology concerns the necessity of applying model se-

lection criteria to estimate the number of components

in the mixture. For multiple ﬁber proﬁles, the ﬁt-

ting process has to be applied repeatedly to different

conﬁgurations before the best ﬁnal decision is esti-

mated. This algorithmic process entails higher time-

complexities than deterministic ones.

We believe that the directional statistics technique

proposed in this work offers signiﬁcant increases in

sensitivity for anatomical analysis over traditional ap-

proaches. We intend to build on the quantitative and

qualitative information provided by the proposed di-

rectional statistics approach to support the study of

ﬁber tract architecture in the brain. In particular, this

information may be explored to build robust prob-

abilistic tractographic algorithms for complex ﬁber

conﬁgurations.

REFERENCES

Adler, D. and Murdoch, D. (2010). rgl: 3D Visualiza-

tion Device System (OpenGL). R package version

0.92.879.

Banerjee, A., Dhillon, I. S., Ghosh, J., and Sra, S. (2005).

Clustering on the Unit Hypersphere using von Mises-

Fisher Distributions. Journal of Machine Learning

Research, 6:1345–1382.

Basser, P. J., Pajevic, S., Pierpaoli, C., Duda, J., and Al-

droubi, A. (2000). In Vivo Fiber Tractography Us-

ing DT-MRI Data. Magnetic Resonance in Medicine,

44:625–632.

Cho, K.-H., Yeh, C.-H., Tournier, J.-D., Chao, Y.-P., Chen,

J.-H., and Lin, C.-P. (2008). Evaluation of the accu-

racy and angular resolution of q-ball imaging. Neu-

roImage, 42:262–271.

Descoteaux, M., Deriche, R., Kn¨osch, T. R., and Anwan-

der, A. (2009). Deterministic and Probabilistic Trac-

tography Based on Complex Fibre Orientation Dis-

tributions. IEEE Transactions on Medical Imaging,

28(2):269–286.

Hornik, K. and Gr¨un, B. (2011). Mixtures of von Mises

Fisher Distributions. R package version 0.0-0.

Jian, B., Vemuri, B. C.,

Ozarslan, E., Carney, P. R., and

Mareci, T. H. (2007). A novel tensor distribution

model for the diffusion-weighted MR signal. Neu-

roImage, 37:164–176.

Jiang, H., Golay, X., van Zijl, P. C., and Mori, S. (2002).

Origin and minimization of residual motion-related

artifacts in navigator-corrected segmented diffusion-

weighted EPI of the human brain. Magnetic Reso-

nance in Medicine, 47:818–822.

Kuo, L.-W., Chen, J.-H., Wedeen, V. J., and Tseng, W.-Y. I.

(2008). Optimization of diffusion spectrum imaging

and q-ball imaging on clinical MRI system. NeuroIm-

age, 41:7–18.

Lenglet, C., Campbell, J. S. W., Descoteaux, M., Haro, G.,

Savadjiev, P., Wassermann, D., Anwander, A., De-

riche, R., Pike, G. B., Sapiro, G., Siddiqi, K., and

Thompson, P. M. (2009). Mathematical methods for

diffusion MRI processing. NeuroImage, 45(1, Supple-

ment 1):S111–S122.

Mardia, K. V. and Jupp, P. (2000). Directional Statistics.

John Wiley and Sons Ltd., 2nd edition.

Mori, S. and van Zijl, P. C. M. (2002). Fiber tracking:

principles and strategies - a technical review. NMR

in Biomedicine, 15:468–480.

Ozarslan, E., Shepherd, T. M., Vemuri, B. C., Blackband,

S. J., and Mareci, T. H. (2006). Resolution of complex

tissue microarchitecture using the diffusion orienta-

tion transform (DOT). NeuroImage, 31:1086–1103.

Polzehl, J. and Tabelow, K. (2011). dti: Beyond the Gaus-

sian Model in Diffusion-Weighted Imaging. Journal

of Statistical Software, 44(12).

R Development Core Team (2010). R: A Language and

Environment for Statistical Computing. R Foundation

for Statistical Computing, Vienna, Austria.

Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann,

C. F., Behrens, T. E. J., Johansen-Berg, H., Bannis-

ter, P. R., Luca, M. D., Drobnjak, I., Flitney, D. E.,

Niazy, R. K., Saunders, J., Vickers, J., Zhang, Y., Ste-

fano, N. D., Brad, J. M., and Matthews, P. M. (2004).

Advances in Functional and Structural MR Image

Analysis and Implementation as FSL. Technical Re-

port TR04SS2, FMRIB (Oxford Centre for Functional

Magnetic Resonance Imaging of the Brain).

Yeh, F.-C., Wedeen, V. J., and Tseng, W.-Y. I. (2010). Gen-

eralized q-Sampling Imaging. IEEE Transactions on

Medical Imaging, 29(9):1626–1635.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

714