An Approach to Simplify Navigation within Ontologies

Karina Robles

, Alejandro Ruiz

, Anabel Fraga

and Juan Llorens

Carlos III University of Madrid, Madrid, Spain

University of Piura, Piura, Peru

Abstract. Semantic Web technologies have contributed mainly to organize the

knowledge and to search about this organized knowledge. One of the most

complex search is to know if two entities are related within a ontology. These

are called Semantic Associations, which have been classified using operators:

-path, -join and -iso. Then, a -query will solve any of them.

Studies about this area offer low performance execution times, but others

increase the performance with pre-processing, making use of complex

structures in memory. In this paper, we present semantic associations and

analyze related studies. We focus on design a simplified representation of the

ontology that facilitates the navigation and reduce the algorithms complexity to

solve these operators, starting from the first of them: -path.

1 Introduction

To search anything and everywhere became a common habit in the human being, but

finding what it is needed is a hard work because of the information increasing.

However, many tools are available in order to accomplish this task, which nowadays

are based on Semantic Web technologies, i.e. using the ontology. Due to the Semantic

Web, search is not only about the concepts (or entities) but also about the

relationships between them, i.e. finding how two entities are related.

Although, ontologies (in general, Semantic Web Technologies) lead the researches

to find new ways of searching, such as new visual interfaces to help the user in

semantic queries [1–7] or semantic query languages (RQL [8], SquishQL [9],

TRIPLE [10] and others [11–13]), the kind of search described above is not solved

completely by those. Those approach need that the user knows how the resources or

entities are related.

Two entities can be connected by relationships and other entities, which is why it

is a complex thing, especially when these two entities are too far within the ontology.

These complex relationships are called Semantic Associations and they have been

studied and classified using the  operators: -path, -join and -iso. To solve them,

ontology relationships in the path between X and Y should be evaluated, and also, the

entities connected by these relationships [14–17]. Therefore, this problem is about

finding path problems between nodes in a graph, due to this kind of representation

(the graph) is the main syntax of the ontology [9], [18–20].

Consequently, it is about retrieving the set of complete paths of the ontology graph

that fits the user query in execution time, or even confirm that a path is available.

Robles K., Ruiz A., Fraga A. and Llorens J..

An Approach to Simplify Navigation within Ontologies.

DOI: 10.5220/0004178500440053

In Proceedings of the 3rd International Workshop on Software Knowledge (SKY-2012), pages 44-53

ISBN: 978-989-8565-32-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Therefore, a new approach has been developed in this paper based on a

transformation of the ontology graph; which is explained in section 4. We believe that

a new representation of the ontology graph will facilitate the navigation and also the

algorithms to solve  operators.

2 The Ontology Graph

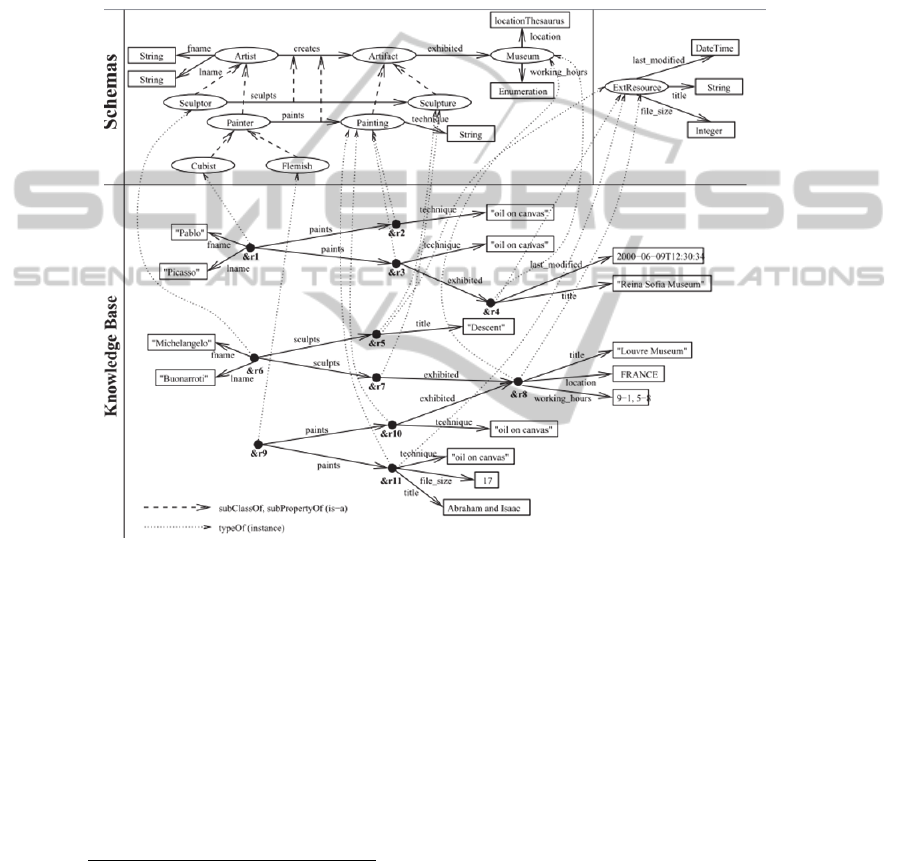
Fig. 1. Example of RDF graph.

The RDF

ontology can be modeled like a tagged directed graph, where triplets

(Subject, Property, Object) are represented by an arc tagged with the name Property

connecting the nodes Subject and Object [8], [9], [20], [21]. Therefore, the ontology

navigation is about traverse the graph ontology. However, the ontology graph has to

be built following the RDF definitions: Property types and classes are defined en the

RDF schema (top part of Fig.

), where a property is described by a domain (the set of

classes the property applies to) and a range (the literal type or classes with values).

Classes are defined by their relationships with other classes, i.e. by the property

rdfs:subclassOf, to be in the right order inside the hierarchy. Also, properties can be

organized in hierarchies using the property rdfs:subproperty, and the resources are

Resource Description Framework is a family of World Wide Web Consortium (W3C) specifications,

originally designed as a metadata data model.

defined by their relationships with other resources and by the relationship with the

classes because they are instances of this classes. Then, the graph ontology built

following those definitions will be very complex and the algorithms to navigate this

graph will be computationally expensive [22].

Fig.

1 is an example of a part of an ontology represented by a tagged directed

graph. This figure shows at the top part, the ontology schemas (two schemas in this

case). At the bottom part, there is the data level or the information level, which is

mostly about the instances of schema items.

2.1 Semantic Associations

The Semantic Associations were defined formally in [14], [15] based on the formal

model described in [8]. In summary, semantic associations were specified using the -

operators described below and the



-query will return any of these operators:

 -pathAssociated: Two entities will satisfy this property if there exists a path

between them in the ontology graph, which brings from the first entity to the second

entity or vice versa. For example, in Fig.

1, there is a path between resources &r6 and

&r8 which represents that a sculptor Michelangelo Buonarotti has a sculpture

exhibited in Louvre Museum.

 -joinAssociated: Two entities will satisfy this property if there exists a

connection node between their paths, i.e. the paths converge at some point in the

graph ontology. For example, in Fig.

1, between &r6 and &r9, there is a connection

point which is &r8, which represent that the artifact of this two artists (&r6 and &r9)

are exhibited in the same museum.

 -cpAssociated: Two entities will satisfy this property if they are descendants of

the same class and they are at the same level in hierarchy. For example, in Fig.

1, &r1

and &r6 satisfy this property because they are both artists.

 -isoAssociated: Two entities will satisfy this property if they have similar

characteristics, i.e. their properties and classes are similar. For example, in Fig.

1, &r1

and &r6 are -isomorphic, because they both represent an artist, which creates

artifacts exhibited in a museum.

3 Related Work

In this section we describe some approaches that could be used to solve the

operators. Firstly, we describe some graph algorithms that could be applied for this

and secondly, some indexing structures approaches.

3.1 Transitive Closure Computation Algorithms

Due to the graph representation of the ontology, a RDF triple (Subject, Predicate,

Object) will play as a binary relation, so the computation of the transitive closure of

binary relations could be applied. There are two types of approaches to cope with it:

firstly, the matrix-based direct algorithms. This approach does the computation

process based on the matrix representation of graph relations.

Several algorithms are in this area, such as [23], solved by linear algebra using

Gauss-Jordan and Aitkeen methods, with a O(n

) complexity, or [24], where Tarjan

solved the problem of finding path expressions applied to the single source path

expression problem

. This study leads him to a demonstration in [25] about the

mapping of this path expressions to all sorts of path problems, e.g. the shortest path

search problem.

Hence, a technique that solves the single source path expression problem can be

introduced and taken it as a universal solution to the problem of searching Semantic

Associations as Barton proposed [16], [17], [26]. However, the Warshall algorithm

[27] is the base of the matrix-based algorithms. It computes the transitive closure by

traversing the matrix from the top left corner to the bottom right one.

Secondly, graph-based direct algorithms which normally work with directed

acyclic graph

(DAG). A Tarjan transformation of an arbitrary directed graph into

DAG [28] could be considered to apply this approach. It is about to identify strongly

connected components and replacing them with a single node (collapsing them). The

base of this kind of algorithms is found in [29] where processes nodes in reverse

topological order, and obtain a condensed acyclic graph. Other works [30]

demonstrate how Tarjan’s algorithm could be improved (in the process order).

Finally, we can find hybrid algorithms which mix two ideas above. For instance,

algorithms in [31] works in two phases: First, the condensed graph is obtained by

collapsing each strongly connected components, and, at the same time, the topological

sort is obtained. In the second phase, the transitive closure is computed using an

adjacency matrix

. They use an algorithm similar to the Warshall’s but it is breadth-

first algorithm different from those graph-based algorithms (mostly depth-first) [32].

3.2 Index Graph Traversal

The studies in [14], [15] uses a Schema Path Index (SPI) which provides fast access

to all possible paths between two classes in a schema, because the ontology has the

schema part relative smallest than data. However, there are paths that involve

resources that belong to the data layer.

They tried to manage these situations and offer the InterClass Index (ISI). This

index stores the information about the schemas that are linked due to multiple

classifications (for example, in Fig.

1, &r4 has a multiple classification, because it

belongs to Museum and Ext. Resource classes), but before they export the nodes at

the data layer to the schema layer using artificial nodes that collapse the two class

nodes.

Consequently, when a query involves resources that belong to classes (that do not

have any paths between them or belong to different schemas), the ISI is searched to

Given a graph G = (V,E) and a distinguished source vertex s, find a regular expression P(s, v) for each

vertex v which represents all paths from s to v in G.

It is a directed graph with no directed cycles, i.e. there is no way to start at some vertex v and follow a

sequence of edges that eventually loops back to v again

An n x n adjacency matrix of elements a

of a graph having n nodes is a matrix with a

having the value of

1 if there is an arc between i and j, and 0 otherwise.

find candidate nodes that if collapsed may result in a path. If no candidate node exists,

an empty set is returned as a result. This idea here is finding all alternative paths that

reach the terminus node from the origin node, and evaluating each one to get the final

result according the  operator searched. To do that, they do a pre-process to store all

paths between classes at the schema level in matrices. Thus, the computational

complexity will be O(|V|

|V|

) [32].

Another research [16], [17] propose an index of a condensed graph. The complete

graph is transformed recursively to get a tree or a forest of trees, by collapsing the

strongly connected components into a single node, i.e. uses the hybrid-based

algorithms ideas. In each transformation, an extended signature is created to store the

information about the nodes that were problematic.

They focus on the design of a new index structure and specially on solving ρ-

pathAssociated and ρ-joinAssociated under the idea that searching a tree is easier than

searching a graph. They based on the signature defined for trees in [33]. The

information of the transformation is stored in two inverted files: one with the multiple

nodes and their corresponding signatures, and the second with the signature with the

list of multiple nodes. At the end, they affirm that the transforming time of the

ontology into the forest of tress is about O(2n) and the creation time of the signature

for each node is O(n). These times are smallest than [15].

To solve the ρ-pathAssociated, they present an algorithm that works in one

direction. However the algorithm to solve ρ-joinAssociated is based on evaluating

each multiple node, finding if there is a path between this multiple node and each

node the origin and the terminus. Hence, this algorithm will have high computational

times.

This work uses a matrix in each transformation to represent the transitive closure.

Though, the final graph is smallest than the original, at the end the process of

searching semantic associations have to extend recursively each component to get the

original graph. Therefore, the computational time depends of the size of the matrices

in each transformation. They called this approach as -index [26].

4 Our Approach

The transitive closure algorithms could be applied but do not solve the problem of

returning paths under certain conditions. They obtain all the paths between nodes in

the original graph. That is why other approaches, although they use some of transitive

closure algorithms, they create specific indexes by preprocessing the graph. This idea

is the most interesting part of the related research section. Another important point

will be the transformation of the graph to simplify the algorithms. Therefore, we

present a transformation that will be obtained in a previous graph processing.

4.1 Transforming into a DAG

We consider approaches in [16], [17], but we follow a different idea. Instead of

collapsing the strongly connected components, we make copies of the important

nodes inside them, located these copies under the node on which they depend. It is

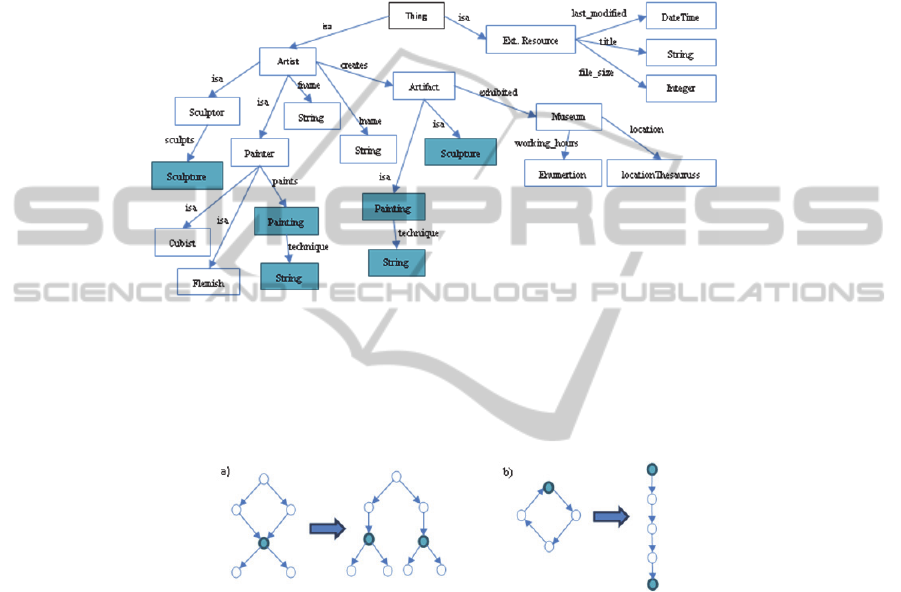
also about to obtain a forest of tree, where exits a root node and all the real nodes are

dependent of it, so there will not be a recursive process.

Therefore, a node that belongs to two or more classifications, i.e. two or more

classes, will be duplicated in the new graph and each copy will be located depending

of the corresponding classification. As it is shown in Fig.

, the nodes Sculpture and

Painting are duplicated due to their multiple classifications, and also the node String

that depends of Painting.

Fig. 2. Example of Transformation into DAG.

Fig.

is an example of a transformation of the schema part of the ontology in Fig.

, but also, the data layer will be transformed following these ideas. The root node

will be always the node Thing. Therefore, at the end we obtain one model which

represents all the ontology.

Fig. 3. Transformation of graph cycles.

We also recognize the graph cycles which maybe exist in the ontology [16], but in

our case, the node will be copied many times as it is necessary to represent its

dependence respect the other nodes, as it is shown in Fig.

4.2 Transformation into a Numeric Representation

In the Semantic Search area, a field that involves Semantic Associations, we can find

some representations, especially in complex search as [34]. They uses suffix arrays to

process all the paths in the ontology graph. They use only DAG with algorithms with

O(|R||E|), i.e. the resources in G. They assign number to the nodes for a quick access.

Another research [35] is based on solve the transitive of hierarchical relationships

(is-a) in KOS (Knowledge Organization Systems). One of their objectives is support

the modifications of the ontology structure, because although they are less frequent,

they should be solved with a minor cost. An interesting objective we share and we try

to follow in our representation.

They apply a compression schema for trees which they called range compression.

It is based on assign numbers to nodes according to their post-order. Then, each node

will have an index that contains the minor post-order number of its descendants which

with its post-order form an interval. Besides, each node will have the intervals of the

nodes that can be reached and are in other tree, i.e. with a different post-order.

At the end, they increment the intervals in order to reflect the ontology

modifications at minor cost. For example, the interval [1,5] will be [10,50]. This work

gives us an idea of its application to semantic associations, especially to solve the -

pathAssociation. The intervals will be evaluating to know if two nodes are connected

and the paths will be obtained easily.

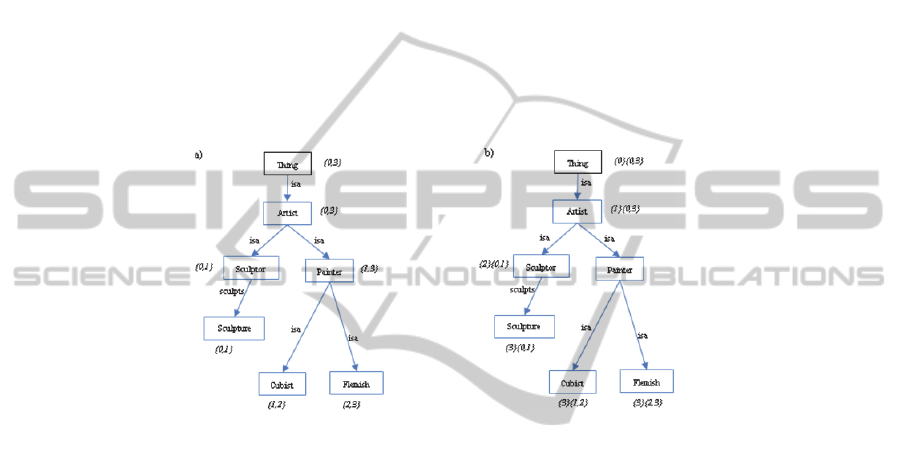
Fig. 4. Numeric representation.

Therefore, we base our work on the preceding ideas. To create our index, we

traverse the graph following the preorder. So, we begin in the root node, assigning to

it 0. Then, we visit the left node assigning to it the same: 0. If this node does not have

descendants, the second number of the index will be the first number plus 1.

After that, we visit the right node, which will have the first number of the index

equal to the second number of the left node, and its second number will be the first

number plus 1 if it has not more descendants. At the end, we will visit each node

twice if it has descendants and once if it has not. Finally, the root will have the second

number equal to the mayor second number of its descendants.

Fig.

a represents a part of ontology transformed in Fig.

with a numeric index

(an interval), following the instructions we have described before. As we can observe,

to solve the -pathAssociation, we just could evaluate the indexes of the nodes and

find if one of them is within the interval of the other, e.g., Sculpture and Artist.

However, in this representation there are many nodes with the same indexes that

could lead us to confusion when nodes have to be located. Due to the necessity of a

unique representation of each node, we introduce the level of dependency to the root,

as it is shown in Fig.

b. Additionally, because one of our objectives is to manage

future ontology modifications with a minor cost, we will leave some space in the

intervals. Therefore, if a node or several nodes are added like descendant of another

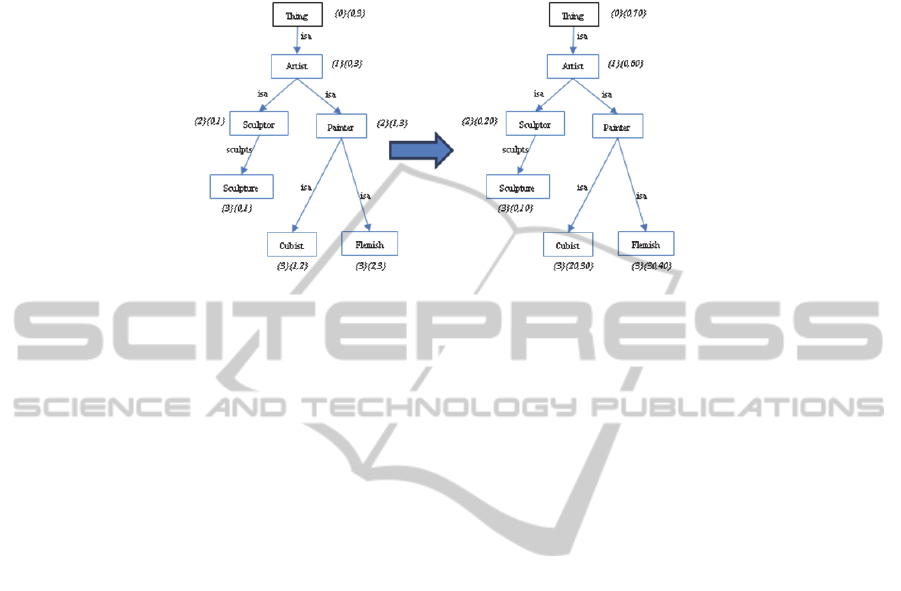
node, they could take as intervals the numbers in the space. Fig.

shows the new

representation.

Fig. 5. Numeric Representation with space.

5 Proposed Evaluation

Because this paper is only at proposal stage, in this section we will describe the

experiments planned to prove it:

- Experiment 1: Comparison between preprocessing times, execution times and total

times for each technique applied to one ontology. We expect to obtain the same

results for each -operator in each technique, but with different times. Our technique

is expected to perform better than the others.

- Experiment 2: Comparison between execution times for each technique applied to

different size ontologies. We expect to get a higher time with a larger ontology. We

will demonstrate that our times are smallest.

- Experiment 3: Comparison between total times for each technique applied to a

modified ontology. We expected that the ontology modification makes the other

techniques do the whole process again. Our technique will need a little adjust.

- Experiment 4: Comparison between algorithms to calculate the space within

intervals. We expected to choose the optimal algorithm to support future changes in

ontology.

6 Conclusions

To solve Semantic Associations is a very complex task that needs high computational

capabilities, because of the nature of the graph ontology. A transformation of this

graph is presented in this paper which simplifies the navigation. This transformation

is obtained by two phases: first, we transform the graph into a DAG, and second, we

assign a numeric representation to each node.

The created index (i.e. the numeric representation) is based on an interval and the

level of root dependence. It will facilitate the construction of algorithms regarding to

the resolution of  operators. An example of the procedure of one algorithm for -

pathAssociation is mentioned: a path between two entities is finding when one of

them is within the interval of the other and with different level of dependence.

Future works will base on development the rest of the  operators. Besides, we

need to do real experiments in a framework by implementing all the semantic

associations’ approaches and compare us with each of them to measure time and

complexity of each technique.

References

1. N. Athanasis, V. Christophides, and D. Kotzinos, “Generating On the Fly Queries for the

Semantic Web : The ICS-FORTH Graphical RQL Interface ( GRQL ) 1,” in Proceedings of

the Third International SemanticWeb Conference, 2004, pp. 486–501.

2. T. Catarci, P. Dongilli, T. D. Mascio, E. Franconi, G. Santucci, and S. Tessaris, “An

ontology based visual tool for query formulation support,” in Proceedings of the 16th

Eureopean Conference on Artificial Intelligence, 2005, pp. 308–312.

3. L. Zhang, Y. Yu, J. Zhou, C. Lin, and Y. Yin, “An Enhanced Model for Searching in

Semantic Portals,” in WWW ’05: Proceedings of the 14th international conference on

World Wide Web, 2005, pp. 453-462.

4. D. A. Koutsomitropoulos, R. B. Domenech, and G. D. Solomou, “A Structured Semantic

Query Interface for Reasoning-Based Search and Retrieval,” in Proceedings of the 8th

extended semantic web conference on The Semantic Web: research and applications, 2011,

pp. 17-31.

5. K. Möller, L. Dragan, and S. Handschuh, “A Visual Interface for Building SPARQL

Queries in Konduit,” in 7th International Semantic Web Conference, 2008.

6. P. R. Smart, A. Russell, D. Braines, Y. Kalfoglou, J. Bao, and N. R. Shadbolt, “A Visual

Approach to Semantic Query Design Using a Web-Based Graphical Query Designer,” in

Proceedings of the 16th international conference on Knowledge Engineering: Practice and

Patterns, 2008.

7. G. Zenz, X. Zhou, E. Minack, W. Siberski, and W. Nejdl, “From Keywords to Semantic

Queries — Incremental Query Construction on the Semantic Web,” Web Semantics:

Science, Services and Agents on the World Wide Web, vol. 7, no. 3, 2009.

8. G. Karvounarakis, S. Alexaki, V. Christophides, D. Plexousakis, and M. Scholl, “RQL : A

Declarative Query Language for RDF,” in Proceedings of the 11th International World

Wide Web Conference (WWW2002), 2002.

9. L. Miller, A. Seaborne, and A. Reggiori, “Three Implementations of SquishQL , a Simple

RDF Query Language Three Implementations of SquishQL , a Simple RDF Query

Language,” in Proceedings of the First International Semantic Web Conference on The

Semantic Web, 2002, pp. 423– 435.

10. M. Sintek and S. Decker, “TRIPLE - a query, inference, and trans- formation language for

the semantic web,” in Proceedings of the First Inter- national Semantic Web Conference on

The Semantic Web, 2002, pp. 364–378.

11. R. Fikes, P. Hayes, and I. Horrocks, “OWL-QL – A Language for Deductive Query

Answering on the Semantic Web,” Web Semantics: Science, Services and Agents on the

World Wide Web, vol. 2, no. 1, pp. 19-29, 2004.

12. V. Haarslev, M. Ralf, and M. Wessel, “Querying the Semantic Web with Racer + nRQL,”

in Proceedings of the KI-2004 International Workshop on Applications of Description

Logics, 2004.

13. R. V. Guha, “rdfDB : An RDF Database.” [Online]. Available:

http://www.guha.com/rdfdb/. [Accessed: 30-Jun-2012].

14. K. Anyanwu and A. Sheth, “The ρ Operator : Discovering and Ranking Associations on the

Semantic Web,” ACM SIGMOD Record, vol. 31, no. 4, pp. 42-47, 2002.

15. K. Anyanwu and A. Sheth, “The ρ-Operator : Enabling Querying for Semantic Associations

on the Semantic Web .,” in Proceedings of the 12th International Conference on World

Wide Web, 2003.

16. S. Barton, “Designing Indexing Structure for Discovering Relationships in RDF Graphs,”

in Database, Texts, Specifications and Objects Workshop (DATESO), 2004, pp. 7-17.

17. S. Barton, “Indexing Structure for Discovering Relationships in RDF Graph Recursively

Applying Tree Transformation,” in Semantic Web Workshop at 27th Annual International

ACM SIGIR Conference, 2004, pp. 58-68.

18. G. Wu, J. Li, L. Feng, and K. Wang, “Identifying Potentially Important Concepts and

Relations in an Ontology,” in Proceedings of the 7th International Conference on The

Semantic Web (ISWC ’08), 2008, vol. 5318, pp. 33-49.

19. R. Rada, H. Mili, E. Bicknell, and M. Blettner, “Development and Application of a Metric

on Semantic Nets,” IEEE Transactions on Systems, Man and Cybernetics, vol. 19, no. 1,

1989.

20. P. Hayes, “RDF Model Theory.” [Online]. Available: http://www.w3.org/TR/rdf-mt.

[Accessed: 30-May-2012].

21. O. Lassila and R. Swick, Resource Description Framework: Model and Syntax

Specification. 1999.

22. M. Hildebrand, J. V. Ossenbruggen, and L. Hardman, “An Analysis of Search-based User

Interaction on the Semantic Web,” Information Systems, no. INS–E0706, pp. 1386–3681,

2007.

23. R. C. Backhouse and B. A. Carré, “Regular Algebra Applied to Path-finding Problems,”

Journal of the Institute of Mathematics and Applications, vol. 15, pp. 161-186, 1975.

24. R. E. Tarjan, “Fast Algorithms for Solving Path Problems,” Journal of the ACM, vol. 28,

no. 3, pp. 594-614, Jul. 1981.

25. R. E. Tarjan, “A Unified Approach to Path Problems,” Journal of ACM, vol. 28, no. 3, pp.

577-593, 1981.

26. S. Barton and P. Zezula, “ρ-index – An Index for Graph Structured Data,” in 8th

International Workshop of the DELOS Network of Excellence on Digital Libraries, 2005,

pp. 57–64.

27. S. Warshall, “A Theorem on Boolean Matrices*,” Journal of ACM, vol. 9, no. 1, pp. 11-12,

1962.

28. R. E. Tarjan, “Depth first search and linear graph algorithms,” SIAM Journal of

Computing, pp. 146-160, 1972.

29. P. Walton Purdom, “A transitive closure algorithm,” BIT, vol. 10, pp. 76-94, 1970.

30. Y. E. Ioannidis and R. Ramakrishnan, “Efficient Transitive Closure Algorithms,” in

Proceedings of the Fourteenth International Conference on Very Large Data Bases, 1988,

pp. 382-394.

31. R. Agrawal, “Hybrid Transitive Closure Algorithms,” in 16th International Conference on

Very Large DataBases, 1990, pp. 326-334.

32. S. Barton, “Indexing Graph Structured Data,” Masaryk University, 2007.

33. P. Zezula, G. Amato, F. Debole, and F. Rabitti, “Tree Signatures for XML Querying and

Navigation,” in In 1st International XML Database Symposium, 2003, pp. 149-163.

34. A. Matono, T. Amagasa, M. Yoshikawa, and S. Uemura, “An Indexing Scheme for RDF

and RDF Schema based on Suffix Arrays,” in Proceedings of SWDB’03, The first

InternationalWorkshop on SemanticWeb and Databases, Colocated with VLDB 2003,

2003.

35. R. Agrawal, A. Borgida, and H. V. Jagadish, “Eficient Managemente of Transitive

Relationships in Large Data and Knowledge Bases,” in Proceedings of the 1989

ACMSIGMODi nternational con- ference on Management of data, 1989, pp. 253-262.