A Genetic Algorithm to Study a P3 Non-trivial Collective Task

F. Jim´enez-Morales

and J. L. Guisado

Dep. F´ısica Materia Condensada, University of Sevilla, Avda. Reina Mercedes s/n, Sevilla, Spain

Departamento de Arquitectura y Tecnolog´ıa de Computadores, Universidad de Sevilla, Sevilla, Spain

Keywords:

Cellular Automata, Genetic Algorithm, Non-trivial Collective Behaviour, Period-3.

Abstract:

Here we report new results of a genetic algorithm (GA) used to evolve one dimensional Cellular Automata

(CA) to perform a P3 non-trivial collective behavior task. For this task the goal is to ﬁnd a CA rule that

reaches one ﬁnal conﬁguration in which the concentration of active cells oscillates among three different

values. Though the majority of the best evolved rules belong to the II Wolfram’s class, the GA also ﬁnds rules

of the III and IV classes. The different computational mechanisms used by each rule to synchronize the entire

lattice are analyzed by means of the spatio-temporal patterns generated.

1 INTRODUCTION

Many natural and man-made systems that consist of

a decentralized collection of simple units with local

interaction can display complex emergent behavior.

The term emergent behavior refers to the appearance

in the system’s temporal behavior of information-

processing capabilities that are not explicitly repre-

sented in the system’s elementary components. These

decentralized systems have many advantages when

compared with central control systems and there is

both a practical and a theoretical interest in the study

of how to design such sytems and their interactions in

order to produce a useful emergent behavior.

One of the most popular methods for the analy-

sis of spontaneous emergence of ordered behavior in

spatially extended systems that are locally coupled

is the use of cellular automata (CA) and genetic al-

gorithms (GA) developed by the “Evolutionary Cel-

lular Automata (EVCA)” group of M. Mitchell, J.P.

Crutchﬁeld and their colleagues (Mitchell et al., 1993;

Mitchell et al., 1994; Crutchﬁeld and Mitchell, 1995;

Das et al., 1994; Das et al., 1995). In their studies a

CA performing computations means that the input to

the computation is seen as the initial state of each cell

and the output is the ﬁnal state reached by the iter-

ations. They analyzed two computational tasks such

as the density classiﬁcation and the synchronization

tasks in one dimensional binary CA. For the density

classiﬁcation task the goal is to ﬁnd a CA rule that de-

termines whether or not the initial conﬁguration con-

tains more cells in state 1 than cells in state 0. If it

does, the whole lattice should eventually iterate to the

ﬁxed point conﬁguration of all cells in state 1; oth-

erwise it should eventually iterate to the ﬁxed-point

conﬁguration of all 0s. For the synchronization task

a successful CA will reach a ﬁnal conﬁguration in

which all cells oscillate between all 0s and all 1s on

successive time steps.

In this paper we focus in another computational

task for one dimensional CA such as the period-3 task

in which the goal is to ﬁnd a rule that, starting from a

random initial condition, reaches one ﬁnal conﬁgura-

tion in which the entire lattice oscillates among three

different states. Originally (Jim´enez-Morales, 1999;

Jim´enez-Morales, 2000) this task was successfully

used to study the appearance of non-trivial collective

behavior in three dimensional CA and in (Jim´enez-

Morales et al., 2002) we made a preliminary study

in one dimension, also the computational mechanics

of an evolved rule was fully described in (Jim´enez-

Morales and Tomassini, 2004). In this paper we use

the same evolutionary process to evolve a population

of one dimensional CA to perform the P3 task but we

report here other answer rules that show irregular and

chaotic patterns.

The paper is organized as follows: section 2 de-

scribes the P3 task, section 3 outlines the character-

istics of our genetic algorithm, the results are shown

in section 4 and ﬁnally the conclusions are shown in

section 5.

250

Jiménez-Morales F. and L. Guisado J..

A Genetic Algorithm to Study a P3 Non-trivial Collective Task.

DOI: 10.5220/0004179502500256

In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 250-256

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Four of the best evolved rules, the rule table hexadecimal code, the type of non-trivial collective behavior, the

Langton’s parameter, the ﬁtness function versus the highest one and the Wolfram’s class. To recover the 128-bit string giving

the output bits of the rule table, expand each hexadecimal digit to binary. The output bits are then given in lexicographic order.

The arrangement of neighbours in the genetic algorithm is |s

i−3

i−2

i−1

i+1

i+2

i+3

Symbol Rule Table Hexadecimal Code NTCB λ F(φ)/F(φ

) Wolfram’s

Class

90001c50-27307066-0820a852-25650800 P3 0.3203 0.12 II

21088418-01091108-41038844-10c18080 P3(QP3) 0.2109 0.41 II

f193800-c06b0eb0-e000461c-80659c11 P3 0.3359 0.05 IV

146157d1-fbb53fec-7dfbeffc-eaf0fa28 P3 0.6250 1.0 III

2 THE COMPUTATIONAL P3

TASK

2.1 Cellular Automata

Cellular automata are discrete dynamical systems

consisting of an array of cells, each of which can be

in one of a ﬁnite number k of possible states, up-

dated synchronously in discrete time steps, accord-

ing to a local, identical interaction rule. Here we will

only consider Boolean automata for which the cellular

state s ∈ {0,1}. In this work the regular cellular grid

is one-dimensional, i.e. d = 1. The state of a cell at

the next time step is determined by the current states

of the cell itself and of a surrounding neighborhood

of cells and is given by:

t+1

= φ(s

i−r

...,s

,...s

i+r

) φ : k

2r+1

−→ k (1)

where s

denotes the value of site i at time t, φ rep-

resents the local rule of evolution, and r is the CA

radius i.e., the number of neighbors (cells) on ei-

ther side of a given cell. The conﬁguration of the

entire lattice at a given time t can be described by

= (s

,. . . , s

N−1

), where N is the lattice size.

Periodic boundary conditions s

N+i

= s

are used. To

study the spatio-temporal patterns generated by the

CA dynamics, a global update rule Φ can be deﬁned

which applies in parallel to all the cells s

t+1

= Φ(s

);

and an ensemble operatorΦ

Φ which operates on sets of

lattice conﬁgurations {s

} (Wolfram, 1994).

2.2 Non-trivial Collective Behavior

An interesting situation of emergentbehaviorin CA is

found with the appearance of non-trivialcollectivebe-

havior (NTCB). As CA are governed by local interac-

tions and subjected to noise, it was expected that any

global observable, such as the concentration of acti-

vated cells c(t) =

∑

(t) would show a trivial time

dependence in the limit of inﬁnite size (Bennet et al.,

1990). But several exceptions to this have been found.

The most remarkable one is a quasiperiod three be-

havior (QP3) that exhibits the concentration of rule-

33 automaton in d=3 and other CA in higher space

dimensions (Chat´e and P.Manneville, 1992). This be-

havior is neither transient nor due to the ﬁnite size

of the lattice and has been obtained for deterministic

and probabilistic rules. Several attempts have been

made to understand its phenomenology and have ad-

dressed the possible mechanisms by which this puz-

zling collective behavior emerges but yet there is not

any answer to the question of how NTCB can be pre-

dicted from the local rule. Then in (Jim´enez-Morales,

1999) we proposed using a genetic algorithm to the

search in d=3 of CA rules with QP3 periodicity and in

(Jim´enez-Morales and Tomassini, 2004) the same al-

gorithm was used in d=1. Quasiperiodicity is the most

interesting non-trivial collective behavior but in d=1

can only be observed under some speciﬁc conditions.

Here we will focus mainly in period-3 collective be-

havior. As stated before for this P3 task the goal is

to ﬁnd a rule for wich the concentration is oscillating

among three different values, i.e., c(t) = c(t + 3).

3 THE GENETIC ALGORITHM

Our GA begins with a population of P = 20 randomly

generated chromosomes, listing the rule-table output

bits in lexicographic order of neighborhood patterns.

We consider binary CA with periodic boundary con-

ditions. Each CA is represented by a bit string delin-

eating its rule table φ, containing the output bits for all

possible neighborhood conﬁgurations. The bit string

is of size 2

= 128, resulting in a huge space of 2

128

possible rules. The ﬁtness evaluationfor each CA rule

is carried out on a lattice of N cells starting from a

random initial condition of concentration 0.5. After a

transient time of N/2 time steps, we allow each rule

to run for a maximum number of M iterations. The

AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask

251

values of concentration are assembled in groups of 4

consecutive values, noted as c

to c

, and the ﬁtness

function F(φ) is deﬁned by:

F(φ) =

M/4

∑

abs[(c

−c

)(c

−c

)−(c

−c

)(c

−c

)]

(2)

The rule’s ﬁtness F(φ) is taken from a geometrical

point of view and it is an average area in the iterative

map, i.e. the graph of c(t + 1) versus c(t). In this

iterative map the area of a period-2 behavior is too

small, almost 0, the area of a noisy period-1 and the

area of an intermittent P2 is higher than that of a P2

and ﬁnally a P3 and quasiperiod-3 behaviors have the

highest values.

In each generation: (i) F(φ) is calculated for each

rule φ in the population. (ii) The population is ranked

in order of ﬁtness. (iii) A number E = 5 of the highest

ﬁtness (“elite”) rules are copied without modiﬁcation

to the next generation. (iv) The remaining P− E = 15

rules for the next generation are formed by single-

point crossover between randomly chosen pairs of

elite rules. The off-springs from each crossover are

each mutated with a probability m = 0.05. This de-

ﬁnes one generation of the GA; it is repeated G = 10

times for one run of the GA.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0 250 500 750 1000

Generation

Figure 1: The λ parameter of the best rule in each genera-

tion versus the generation for the runs in which φ

, φ

and φ

were encountered.

4 RESULTS

We performed more than 200 different runs of the GA

each with a different random-number seed. In d = 1

the GA is able to ﬁnd many rules with the desired

behavior, about 10% of the runs ended up with a rule

that showed a P3 collective behavior or a quasiperiod-

3. Table 1 shows four of the best evolved rules, the

rule table hexadecimal code, the λ parameter ( deﬁned

as the fraction of nonzero output bits in the rule table),

0.24

0.28

0.32

0.36

0.24 0.28 0.32 0.36

c(t+1)

c(t)

(a)

0.2

0.25

0.3

0.35

0.4

0.45

0.2 0.25 0.3 0.35 0.4 0.45

c(t+1)

c(t)

(b)

0.45

0.47

0.49

0.51

0.45 0.47 0.49 0.51

c(t+1)

c(t)

(c)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.1 0.2 0.3 0.4 0.5 0.6 0.7

c(t+1)

c(t)

(d)

Figure 2: The iterative map for the rules: (a) φ

, (b) φ

and (d) φ

. Lattice size is N = 2000 cells. Transient

times are discarded. The collective behavior for the rules

, φ

and φ

is a period-3 behavior. Rule φ

shows two

triangular objects that corresponds to a quasiperiod-3 col-

lective behavior.

the non-trivial collective behavior observed, and the

corresponding Wolfram’s class (Wolfram, 1984).

Figure 1 shows the λ parameter of the best evolved

rule in each generation versus the generation. The ini-

tial population of candidate rules have a random λ be-

tween (0,1). For all runs of the GA in the ﬁrst 250

generations the best selected rule has a λ which has

small differences with the best evolved rule. It has

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

252

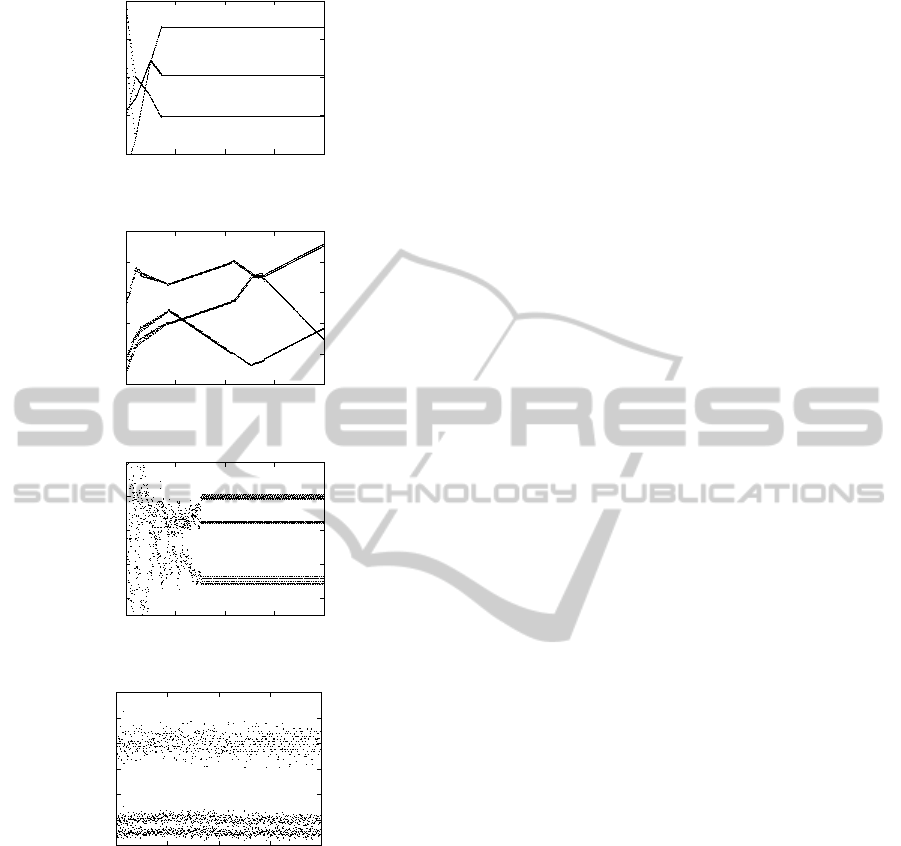
0.2

0.25

0.3

0.35

0.4

0 500 1000 1500 2000

c(t)

(a)

0.2

0.25

0.3

0.35

0.4

0.45

0 500 1000 1500 2000

c(t)

(b)

0.45

0.47

0.49

0.51

0.53

0 500 1000 1500 2000

c(t)

(c)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0 500 1000 1500 2000

c(t)

(d)

Figure 3: The time series of the concentration for the rules

(a):φ

, (b):φ

, (c): φ

and (d):φ

. Lattice size is N = 2000.

The initial condition is a random conﬁguration with concen-

tration 0.5.

been suggested (Langton, 1990) that there is a rela-

tionship between the ability of a CA to show complex

behavior and the λ parameter. The basic hypothesis

was that λ correlates with computational capability in

that rules capable of complex computation must be or

are most likely to be found near some critical value

( λ

≈ 0.26 ) and also that these rules belong to the

Wolfram’s class IV. Our GA has selected rules with λ

that goes from 0.21 to 0.62 and the majority of them

belong to the II class and some others to the III class.

Only in one run the GA encountered a rule of the IV

class, φ

, but it has the lowest ﬁtness. The results from

our evolutionary process do not show any kind of crit-

ical value of λ ( an “edge of chaos” ) for the best ﬁt-

ness rules. In this sense the P3 task conﬁrms the same

result as it was obtained by (Mitchell et al., 1993) for

the density classiﬁcation task.

The behavior of the best evolved rules is shown in

three plots: a) Figure 2 that shows the iterative map,

i.e. the concentration at time t + 1 versus the concen-

tration at time t. In this iterative map transients points

are discarded to better deﬁne the collective behavior.

b) Figure 3 that shows the time series of the con-

centration from the starting time t = 0. And ﬁnally c)

Figure 4 that shows a space-time diagram of 258x300

points after a transient of 200 time steps.

Rules φ

and φ

show a P3 behavior that can be

seen as three well deﬁned clouds of points in the it-

erative map and in the time series of the concentra-

tion, after a transient time, as three different constant

values. The time series of the concentration for rule

is different and shows three branches that interact

and mix among them. This behavior lasts for very

long times and as the lattice size increases the be-

havior is better deﬁned. Now the iterative map rather

than three clouds of points is a triangular object and

the collective behavior of rule φ

corresponds to a

cuasiperiod-three (QP3) behavior (Jim´enez-Morales

and Tomassini, 2004). The rule with the highest value

of the ﬁtness function is φ

. Its concentration also os-

cillates among three values but in a noisy fashion and

its attractor in the iterative map consists in a fuzzy 3-

cycle behavior.

Under the ﬁtness function F(φ) in d = 1 the evo-

lutionary process has selected rules that starting from

a random initial condition synchronize the whole sys-

tem to a state in which the concentration oscillates in a

three-state cycle. But the way in which the four rules

obtain the synchronization is quite different from rule

to rule. To understand those mechanisms we can use

the tools of the “computational mechanics” developed

by Crutchﬁeld and Hanson (Hanson and Crutchﬁeld,

1997). This point of view describes the computa-

tion embedded in the CA space-time conﬁguration in

terms of domains, defects and defect interactions.

Figure 4a,b shows a space-time diagram of the

rules φ

and φ

. Time starts after a transient time of

200 time steps and goes from up down and space is

displayed on the horizontal axis. In the patterns gen-

erated by both rules there are some easily recognized

spatio-temporally periodic background -the domains-

on which some dislocations move. A domain, Λ

Λ, is a

set of conﬁgurations with two properties: (i) temporal

AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask

253

Time

Space

(a)

Time

Space

(b)

Time

Space

(c)

Time

Space

(d)

Figure 4: Space-Time diagram of four answer CA rules for the computational P3 collective task. Lattice size of 258 cells.

Starting from a random initial condition with c(0) = 0.5 the ﬁrst 200 time steps are discarded. It is shown a window of

258x300 points. (a) φ

. This rule of the II class shows a regular and periodic ﬁnal state with two ﬁxed domains; (b) φ

. This

is also a rule of the II class with a periodic background in which defect cells or particles propagate from distant parts of the

lattice; (c) φ

. It can be seen long-lived and irregular propagating defect cells characteristic of the IV class. (d) φ

. This is a

chaotic rule ( III class ) that has the highest ﬁtness.

invariance, which means that for some ﬁnite temporal

period p, Φ

Λ = Λ

Λ; and (ii) spatial homogeneity. In

the simplest case a domain consists of a set of cells in

the space-time diagram that are always repeated; for

example, the domain for rule φ

is shown in Table 2.

If over a long time all the cells of the space-time dia-

gram are in the domain then the concentration of acti-

vated cells will be oscillating among three values 1/2,

1/3 and 1/6. Displacements of the domains along the

temporal or the spatial axis give place to other do-

mains and at the boundaries between them appear de-

fect cells or particles that propagate among the entire

lattice. These defect cells are spatially localized struc-

tures and time-invariant for rules φ

and φ

But the space time diagram of rules φ

and φ

(Figure 4c-d) is not so simple as the previous ones.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

254

Rule φ

also has a periodic background that fulﬁls the

requirements of having a period-3 oscillating concen-

tration, but the main difference with φ

and φ

is the

way the global coordination is acquired. The defect

cells for rule φ

are irregular propagating structures,

which is a characteristic of rules that belong to the IV

Wolfram’s class. And ﬁnally are the patterns gener-

ated by the rule φ

where there is a lack of regularity

or periodic background. While rules φ

, φ

and φ

evolve towards a ﬁnal state in which the concentra-

tion reaches a well determined three state, the three

values of the concentration for rule φ

show a noisy

behavior ( Figure 3d). Rule φ

is a chaotic rule and its

behavior may be interesting from an statistical point

of view, though this is out of the scope of this work.

Table 2: Domain for rule φ

and the concentration.

Space

1 1 0 1 0 0 c

= 1/2

T 1 1 0 0 0 0 c

= 1/3

i 0 1 0 0 0 0 c

= 1/6

m 1 0 0 1 1 0 c

= 1/2

e 0 0 0 1 1 0 c

= 1/3

0 0 0 0 1 0 c

= 1/6

5 CONCLUSIONS

The study of non trivial collective behavior in CA

has suggested a new computational task like the P3

task. A genetic algorithm, with the appropriate ﬁtness

function, has been able to ﬁnd answer rules that have

regular repeating space-time conﬁgurations. These

rules, belonging to the Wolfram’s class II, attained the

global coordination among the entire lattice cells with

propagating structures –particles– that interact among

them until a regular and ﬁnal state is reached. In

the patterns generated by these rules it can be distin-

guished domains and particles like in the density and

the synchronization tasks. And the global coordina-

tion can be explained using the tools of the “computa-

tional mechanics” originally developed by the EVCA

group of Crutchﬁeld and Mitchell.

But our GA has also found some rules ( class III

and IV ) for which the space-time diagrams do not

show a regular pattern. The emergence of a global

computation by these chaotic and complex rules is

very interesting and points out the existence of other

synchronization strategies not well understood yet.

We think that many of the results obtained in tasks

like this one can provide a useful information to es-

tablish a more general framework to study the emer-

gence of global coordination in one dimensional CA.

REFERENCES

Bennet, C. H., Grinstein, G., He, Y., Jayaprakash, C., and

Mukamel, D. (1990). Stability of temporally periodic

states of classical many-body systems. Phys. Rev. A,

41:1932–1935.

Chat´e, H. and P.Manneville (1992). Collective behaviors

in spatially extended systems with local interactions

and synchronous updating. Progress Theor. Phys.,

87(1):1–60.

Crutchﬁeld, J. P. and Mitchell, M. (1995). The evolution of

emergent computation. Proceedings of the National

Academy of Science U.S.A., 92:10742–10746.

Das, R., Crutchﬁeld, J. P., Mitchell, M., and Hanson, J. E.

(1995). Evolving globally synchronized cellular au-

tomata. In Eshelman, L. J., editor, Proceedings of

the Sixth International Conference on Genetic Algo-

rithms, pages 336–343, San Francisco, CA. Morgan

Kaufmann.

Das, R., Mitchell, M., and Crutchﬁeld, J. P. (1994). A ge-

netic algorithm discovers particle-based computation

in cellular automata. In Davidor, Y., Schwefel, H.-

P., and M¨anner, R., editors, Parallel Problem Solving

from Nature—PPSN III, volume 866, pages 344–353,

Berlin. Springer-Verlag (Lecture Notes in Computer

Science).

Hanson, J. E. and Crutchﬁeld, J. P. (1997). Computational

mechanics of cellular automata: An example. Physica

D, 103:169–189.

Jim´enez-Morales, F. (1999). Evolving three-dimensional

cellular automata to perform a quasiperiod-3(p3) col-

lective behavior task. Phys. Rev. E, 60(4):4934–4940.

Jim´enez-Morales, F. (2000). The evolution of 3-d c.a.

to perform a collective behavior task. In Miller,

J., Thompson, A., P.Thompson, and Fogarty, T. C.,

editors, Evolvable Systems: From Biology to Hard-

ware ICES-2000, LNCS 1801, pages 90–102, Berlin.

Springer-Verlag.

Jim´enez-Morales, F., Mitchell, M., and Crutchﬁeld, J.

(2002). Evolving one dimensional cellular automata

to perform non-trivial collective behavior task: One

case study. In Sloot, P., Tan, C. K., Dongarra, J., and

Hoekstra, A., editors, Computational Science ICSS-

2002, LNCS 2331, pages 793–802, Berlin. Springer-

Verlag.

Jim´enez-Morales, F. and Tomassini, M. (2004). Glob-

ally synchronized oscillations in an one-dimensional

cellular automaton. Int. Jour. Modern Physics C,

15(3):409–425.

Langton, C. G. (1990). Computation at the edge of chaos:

Phase transitions and emergent computation. Physica

D, 42:12–37.

Mitchell, M., Crutchﬁeld, J. P., and Hraber, P. T. (1994).

Evolving cellular automata to perform computations:

Mechanisms and impediments. Physica D, 75:361 –

391.

Mitchell, M., Hraber, P. T., and Crutchﬁeld, J. P. (1993). Re-

visiting the edge of chaos: Evolving cellular automata

to perform computations. Complex Systems, 7:89 –

130.

AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask

255

Wolfram, S. (1984). Universality and complexity in cellular

automata. Physica D, 10:1.

Wolfram, S. (1994). Cellular Automata and Complexity.

Addison-Wesley, USA, ﬁrst edition.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

256