Time Window Selection for Improving Error-related Potential Detection
Rousseau Sandra, Jutten Christian and Congedo Marco
Gipsa-lab-DIS, 11 Rue des math
´
ematiques Domaine Universitaire, 38400 Saint-Martin d’H
´
eres, France
Keywords:
Error-related Potential, BCI, Spatial Filtering, Classification.
Abstract:
In this paper we present an experiment enabling the occurence of the error-related potential in high cognitive
load conditions and observe its inter-subject latency variability. We study the single-trial classification of the
error-related potential using spatial filtering. Then we present a new adaptive algorithm for spatial filtering
and time window selection that allows to adapt to error-related potential latency variability and provides better
classification results.
1 INTRODUCTION
The error-related potential (ErrP) is an event-related
potential (ERP) which is generated when a subject
commits or observes the commitment of an error.
It was first reported in 1991 by Falkenstein et al.
(Falkenstein et al., 1991) and has been since the sub-
ject of growing interest. This potential is time-locked
to the observation of the error and is mostly charac-
terized by a negative deflection (Ne) (Gentsch et al.,
2009), followed by a large positivity (Pe) (Steinhauser
and Kiesel, 2011). There exists different kind of Er-
rPs depending on the agent committing the error. In
BCIs we generally observe what is called the inter-
action ErrP which occurs when a subject observe an
external device committing an error and the feedback
ErrP which is observed when a subject commits an
error but becomes aware of it only after external feed-
back. Lately several authors have become interested
in its integration in BCI systems as a control loop, for
example as an error correction system. The integra-
tion of the ErrP in BCIs involves two main operations:
its single trial detection and the use of this informa-
tion to on-line modify the system. Since its signal to
noise ratio (SNR) is very low, as any ERP, the ErrP
can easily be seen by summing up several trials but is
much less detectable on a single-trial basis. However,
the single trial detection of the ErrP is mandatory for
its integration in BCIs. In addition to its low SNR,
ErrP characteristics can also be highly variable from
one subject to another and from one experiment to
another. Thus to ensure satisfying detection rates, it
is necessary to design filtering methods that will in-
crease the ErrP SNR. Moreover, designing subject’s
specific filters could improve detection accuracy. In
this paper, we first present an experiment we designed
to obtain ErrP data in high cognitive load conditions,
enabling us to approximate BCI use conditions. We
study the occurrence of the ErrP and observe its inter-
subject latency variability. Then we classify this po-
tential on a single-trial basis using spatial filtering
methods. Based on our observations of the inter-
subject latency variability we develop a new adaptive
spatial filtering method which allows the selection of
subjects specific time windows in order to improve
single trial detection results. Our method aims at se-
lecting subjects specific time windows based on each
subject signal characteristics and optimized for the
spatial filter we use. We compare the classification
results we obtain with other less adaptive methods.
Finally we comment on the relevance of the selected
time window and its link with our signals characteris-
tics.
2 DATA
2.1 Experiment
The experiment we designed involves a memory
game where performance feedback is given after the
subject answers questions. No specific reward is
given and the experiment is designed so as to induce
a high cognitive load. The experiment involves two
sessions that last approximately half an hour. Each
session consists of six blocks of six trials, for a to-
tal of 72 trials. Stimuli are presented on a computer
screen and consist of digits displayed in square boxes
715
Sandra R., Christian J. and Marco C..
Time Window Selection for Improving Error-related Potential Detection.
DOI: 10.5220/0004181207150720
In Proceedings of the 4th International Joint Conference on Computational Intelligence (SSCN-2012), pages 715-720
ISBN: 978-989-8565-33-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

arranged in circles.
(a) (b)
(c) (d)
Figure 1: Screen shots from the experiment representing
different steps. a) Fixation cross. b) Memorization se-
quence. c) Target digit appearing. d) Feedback report ques-
tion: ’Did you expect this result?’.
Each trial starts with the display of the score for
3000 ms followed by a fixation cross (see Figure
1.a) also displayed for 3000 ms. Then the memo-
rization sequence starts, each memorization consists
in a random sequence of two to nine digits appear-
ing sequentially in random positions (see Figure 1.b).
Subjects are instructed to retain positions of all dig-
its. At the end of the sequence the target digit is
displayed (see Figure 1.c) and subjects have to click
on the box where it has appeared. Once the sub-
ject has answered, the interface waits for 1500 ms
in order to avoid any contamination of ErrP by beta
rebound motor phenomena linked to mouse clicking
(Pfurtscheller, 1981). Then, if the answer is cor-
rect, the chosen box background color turns into green
(”correct” feedback), otherwise it turns into red (”er-
ror” feedback). Subjects are then asked to report if
the feedback (error/correct) matches their expectation
by a mouse click (“yes”/ “no”) (see Figure 1.d). A
random break of 1000 ms to 1500 ms precedes the
beginning of the new trial (see Figure 2).
Figure 2: Time course of one trial.
The number of digits in the sequence is fixed
within blocks (between two and nine) and updated,
according to subjects performance, at the beginning
of each block. The first block starts with four dig-
its. The number of digits is adapted with an algorithm
tuned to allow about 20% of errors for all subjects, re-
gardless the working memory ability and adapting to
fatigue. Between the two sessions the screen is shut
down to allow a rest break of 2 - 3 minutes.
2.2 Participants
25 healthy volunteer subjects participated, 14 males
and 11 females. Subjects were informed of the proce-
dure before the experiment and filled an information
form. All subjects were BCI-naifs at the time of the
experiment and none of them reported neurological or
psychiatric disorders in the past. Due to the presence
of artifacts, four subjects were excluded from analy-
sis. The age of participants ranged from 20 to 30 with
a mean of 24 (±2.5). The mean error rate was equal
to 18 (±4.6)% of the trials.
2.3 Acquisition and Preprocessing
EEG recordings were made from 31 sensors using
the extended 10/20 system. Both earlobes, digi-
tally linked, were used as electrical reference. The
ground sensor was positioned on the forehead. The
impedance of each sensor was kept below 5kΩ. The
EEG was band-pass filtered in the range 0.1-70 Hz
and digitized at 500 Hz using the Mitsar 202 DC EEG
acquisition system. Data were bandpass-filtered be-
tween 1-40 Hz using an order 4 Butterworth filter with
linear phase response. Eye blinks were extracted us-
ing ICA (independent component analysis), (Comon
and Jutten, 2010). SOBI algorithm was used to per-
form ICA. One EOG source was suppressed for each
subject. It was manually selected using both the tem-
poral shape of the source and its topography.
2.4 Observation of the ErrP and its
Latency Variability
In Figure 3 we plot the event-related potential aver-
aged over subjects for correct trials and for error trials
for one second post-stimulus (observation of the er-
ror). We can see that for error trials the ERP is charac-
terized by a sharp negativity (Ne) followed by a small
positivity (Pe) which is consistent with previous re-
ports (Yeung et al., 2005), (Hajcak et al., 2007). In
addition to these peaks one can also see a first posi-
tive peak which has also been reported by (Ferrez and
Mill´an, 2005) in the case of interaction error-related
potential. For correct trials, a negativity is also ob-
served but with a much lower intensity. Let us de-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
716

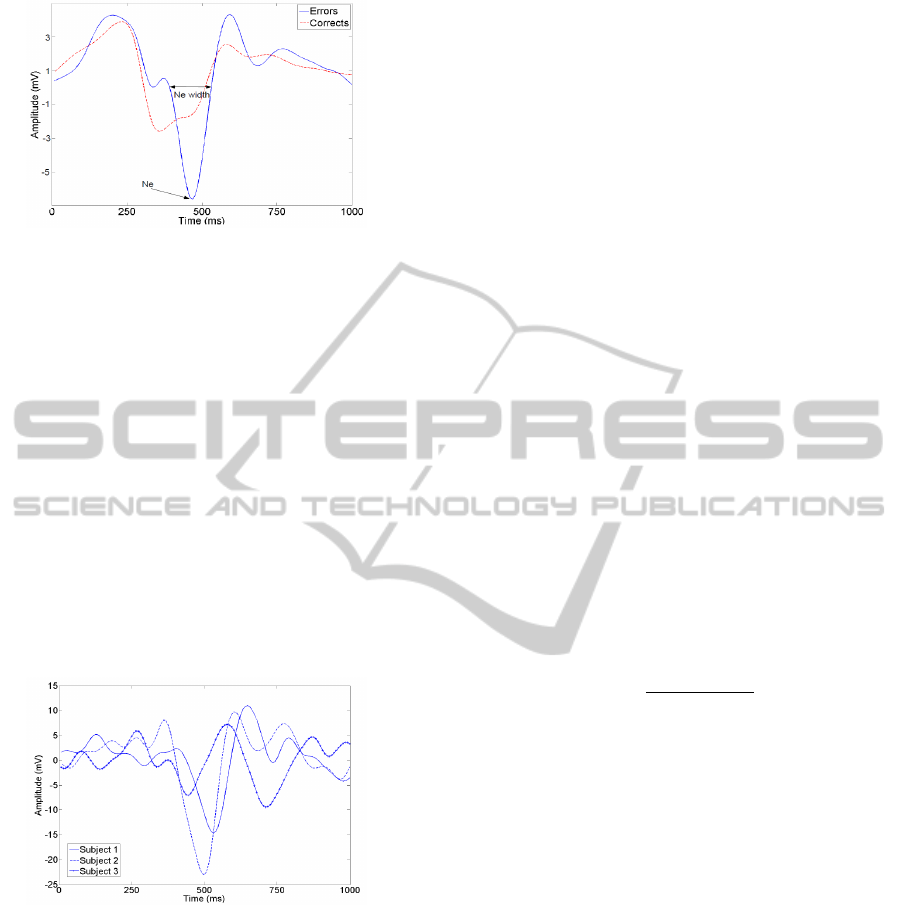
Figure 3: Mean potential averaged over 21 subjects at elec-
trode FCz. Blue thick line corresponds to error trials and
red dashed line corresponds to correct trials.
fine Ne latency as the time where the mean potential
reaches a local minimum in the time window [350 ms
650 ms] and the peak width as the time separating the
last time point where the EEG signal crosses zero be-
fore Ne and the first time point it crosses zero after Ne
as shown in Figure 3. Then the mean Ne latency (over
the 21 subjects) and its standard deviation are 490 ms
±50 ms while the mean peak width is 110 ms. This
shows the high variability of Ne latency since its vari-
ation corresponds to half the width of the peak. In
Figure 4 we plot the mean event-related potentials for
error trials for three different subjects. We can see
that the shape and the latency of this potential can be
highly variable.
Figure 4: Temporal course of the mean error potential for
different subject.Each line corresponds to one subject. Data
are averaged over error trials at electrode FCz.
3 SINGLE TRIAL
CLASSIFICATION
ErrP could be used in BCI systems to detect and cor-
rect error trials. However, to do so, one has to be
able to detect it on a single trial basis. Some authors
already studied this issue (Dal Seno et al., 2010),(Fer-
rez and Mill´an, 2007). Most of them only used raw
data with no spatial filtering. Here we propose to ap-
ply spatial filtering methods to our data in order to try
to improve our classification results.
3.1 Filtering Method
3.1.1 xDAWN Algorithm
Spatial filtering was done using xDAWN algorithm
(Rivet et al., 2008). We consider that the signal is the
sum of one target evoked potential plus other possible
superimposed evoked potentials (but non-target) and
noise:
X =
∑
i
D
i
A
i
+ N (1)
where X represents the signal, D
i
is a Toeplitz matrix
whose first column entries are set to zero except for
those that correspond to the stimuli of type i, A
i
rep-
resents the responses synchronized with the stimuli of
type i and N represents the noise. Evoked responses
A
i
are estimated as:


A
1
...
A
n


= (D
T
D)
−1
D
T
X (2)
with D = [D
1
, D
2
...D
n
].
The aim of xDAWN is to find the filter U which max-
imizes the signal to signal plus noise ratio (SSNR):
U = argmax
Tr(U
T
∑
i
U)
Tr(U
T
∑
X
U)
(3)
with
∑
i
= (D
i
A
i
)
T
(D
i
A
i
) and
∑
X
= X
T
X. This is a
Rayleigh quotient ((Fukunaga, 1990), (Gray, 2006))
which can be solved using the generalized eigenvalue
decomposition (GEVD) of matrices Σ
1
and Σ
X
.
3.1.2 Application to our Problem
In this problem we consider two potentials: one corre-
sponding to the occurrence of an error (the error po-
tential) and one corresponding to the occurrence of
answer display (may it be correct or error). Thus our
signal can be written as :
X = D
1
A
1
+ D
2
A
2
+ N
where D
1
A
1
corresponds to error feedbacks and D
2
A
2
corresponds to feedbacks (errors and corrects). The
evoked potentials are usually defined as a one second
post-stimulus window of the EEG signal. However,
the longer will be this window and the more our po-
tential will contain noise. Thus, it could be interesting
to reduce the size of this window. One way of doing it
is to determine the position of our peak of interest (de-
fined here as Ne) and to select a smaller time window
TimeWindowSelectionforImprovingError-relatedPotentialDetection
717

centered on this peak. However as we have seen be-
fore Ne latency can be highly variable from one sub-
ject to another, making it impossible to select a prior
time window that could be used for all subjects.
3.2 Adaptive Time Window Selection
We propose a modification of xDAWN that allows a
subject’s specific selection of the time window within
the spatial filtering algorithm. Here we span the
whole ERP and find the time window where the tar-
get potential (error trials) contains the most informa-
tion. The time-window will then be used to estimate
the spatial filters and to classify data. Let be L the
length of the window of interest (here set to 250 ms),
N the maximal length of the potential under study
(here 1000 ms) and x the EEG signal of total length
N
T
with N
c
electrodes. Then the proposed algorithm
is as follows:
We first calculate the matrices A
1
∈ R
N×N
c
, D
1
∈
R
N
T
×N
and Σ
X
∈ R
N
c
×N
c
then ∀t ∈ [0, ..N − L]:
• We create matrices D
1new
et A
1new
defined so that
they contain only the signal corresponding to the
window of length L starting at time point t after
the feedback:
D
1new
= D
1
(:, t : t +L) and A
1new
= A
1
(t : t +L, :);
• We create matrix Σ
1new
defined as :
Σ
1new
= (D
1new
.A
1new
)
0
(D
1new
.A
1new
);
• We compute the generalized eigenvalue decompo-
sition (GEVD) of Σ
1new
and Σ
X
(U
t
, λ) = GEV D(Σ
1new
, Σ
X
);
• Finally we define our decision value as:
β(t) = λ(1) (4)
with λ(1) being the first eigenvalue of the GEVD.
The optimal position of our window (t
opt
) is then de-
fined as the time sample corresponding to the maxi-
mum of β. Thus, for spatial filtering we will use filters
computed on this time window (U
t
opt
).
3.3 Preprocessing and Classification
Data were band-pass filtered between 1-10 Hz and
then spatially filtered using the previously described
methods. Data were then classified using Bayesian
LDA classifier (MacKay, 1992). xDAWN algorithm
returns filters classified in descending order of per-
formance thus we used the first two components as
features for our classifier. Data were subsampled at
32 Hz. Data were also classified before spatial filter-
ing using EEG signal from electrodes FCz and Cz as
features, as it has been done in most previous studies
(Ferrez and Mill´an, 2007). Classification was per-
formed on 21 subjects. For each subjects a leave-one
out validation method was used: spatial filters and
classifier were learned on the whole data except one
and then tested on the remaining data.
4 RESULTS
4.1 Evaluation of the Algorithm
In figure 5 we plot the evolution of our decision value
(β) along our window position and the evolution of
our mean classification accuracy. We can see that β is
highly influenced by the window position. Moreover
we can also see that β and our classification accuracy
seem to have a similar evolution. Thus it seems that
the choice of our decision value is relevant for the op-
timization of the single trial detection of the ErrP.
Figure 5: Effect of window position. (a) Evolution of β as
a function of window position. (b) Evolution of classifica-
tion accuracy as a function of window position. Thick line
corresponds to errors, dashed line corresponds to corrects.
4.2 Selection of the Time Window
In figure 6 we plot the mean error potential for three
different subjects and the corresponding selected time
window. We can see that for these three subjects the
shape and latency of the ErrP is very different and
that our algorithm adapts to the shape of the poten-
tial under study and select the time window where the
difference between errors and corrects is huger.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
718

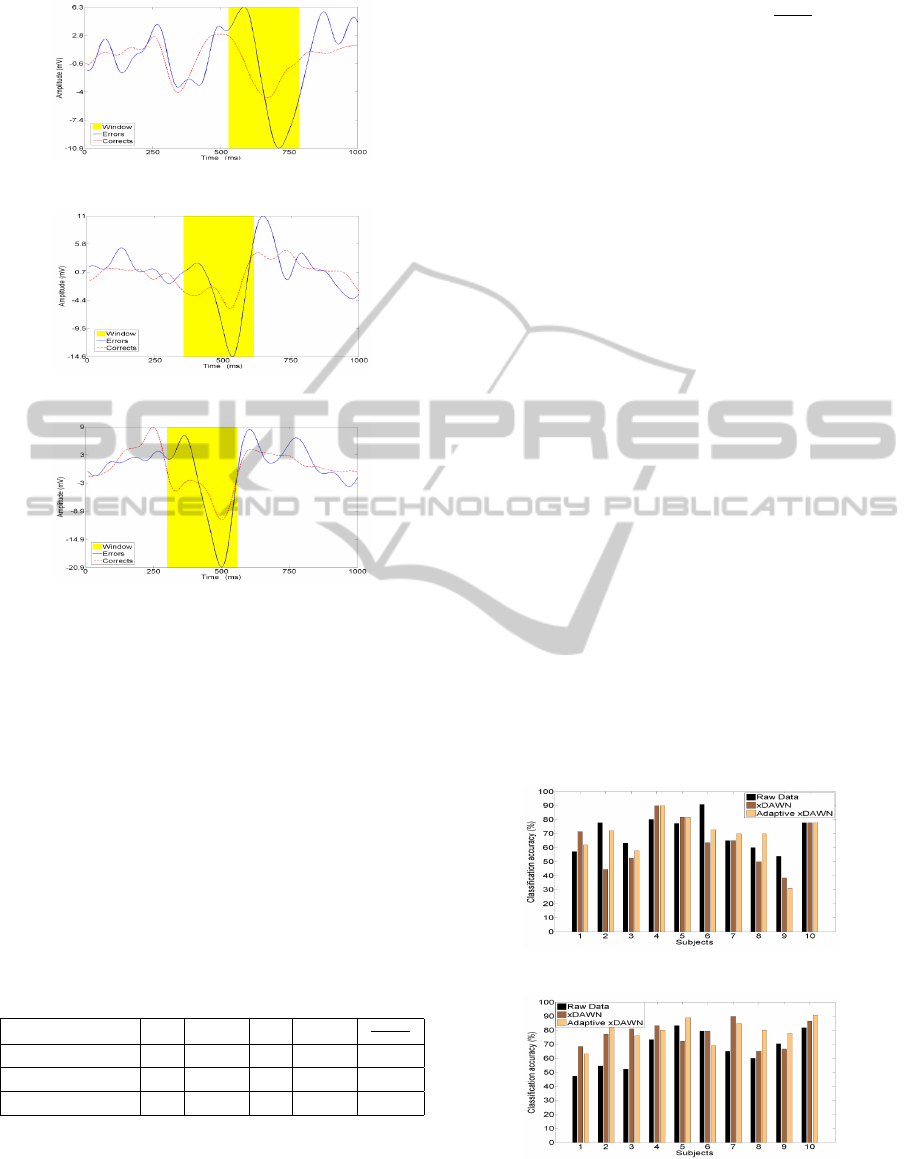
(a) Subject 18.
(b) Subject 7.
(c) Subject 5.
Figure 6: Selected time windows for different subjects. Yel-
low area corresponds to the selected time window. Thick
line is the averaged potential for errors and dashed line is
the averaged potential for corrects, at electrode FCz.
4.3 Classification Results
We report the mean classification results (and their
standard deviation) on table 1 for our three different
methods. It has to be noted that given the very low
number of trials available we get quite encouraging
results even on raw data.
Table 1: Mean classification results. First line corresponds
to classification on raw data, second line to classification
with xDAWN and third line to classification with our adap-
tive xDAWN. Column T
e
gives the classification rate for er-
rors and column T
c
for corrects.
Method T
e
std T
c
std
T
e
+T
c
2
No filtering 66 ± 14 65 ± 10 65.5
xDAWN 56 ± 16 81 ± 7 68.5
New xDAWN 67 ± 19 82 ± 6 74.5
Secondly we can see that xDAWN allows signif-
icantly better classification results for correct trials
than classification on raw data (p ≤ 0.01). However
for classification on error trials xDAWN is worse than
using raw data (p = 0.01). Thus even if xDAWN im-
proves the mean classification rate (
T
e
+T
c
2
), it gives
very poor results for error classification. However for
most types of ErrP integration, correct trials identi-
fication is more important than error trials identifica-
tion. A misidentification of a correct trial (correct trial
is identified as an error trial) will lead to the modifi-
cation of a correct order (and thus leading to an error)
which will diminish our system’s performance. The
misidentification of an error will just lead to no spe-
cific action, which will bring no modification.
Finally it turns out that our adaptive algorithm
gives similar results as the classical xDAWN for cor-
rect trials (p = 0.2) (and thus significantly better than
raw data, p ≤ 0.01) but significantly better results
for error trials (p ≤ 0.01) (and similar as raw data ,
p = 0.3). The main advantage of our method is that it
is optimized for the spatial filter we use and each time
window is selected specifically for one subject. Our
algorithm allows a significant improvement of detec-
tion of correct trials along with no deterioration of er-
ror trials detection (but no improvement) as compared
to classification on raw data. Using this method we
get similar results as those found by previous studies
((Chavarriaga and Mill
´
an, 2010),(Ferrez and Mill´an,
2007)) but with only very small training sets while
other studies used large training sets. This is of great
interest for ErrP integration in BCIs. Indeed one huge
problem in actual BCI systems is the training session
which can be quite long for some applications. Here
we get significant detection results even when using
only 15 error trials (30 trials in total, errors and cor-
rects) which would correspond to a very short training
session.
(a) Error trials.
(b) Correct trials.
Figure 7: Classification results for the first ten subjects. (a)
for error trials. (b) for correct trials. Black bars correspond
to raw data, dark brown bars to xDAWN filtering and light
brown bars to adapative xDAWN filtering.
TimeWindowSelectionforImprovingError-relatedPotentialDetection
719

In figure 7 we plot the classification results for the
ten first subjects for error trials and correct trials us-
ing the different preprocessing methods. We can see
that for classification on error trials xDAWN only out-
performs our adaptive algorithm for two subjects and
for one of them results are very bad for any method.
For correct trials spatial filtering clearly outperforms
classification on raw data, however no clear differ-
ence can be drawn between our two methods, with
xDAWN outperforming the adaptive one for half the
subjects.
5 CONCLUSIONS
In this paper we have studied the error-related poten-
tial and its single-trial detection. We have seen that
the ErrP did occur even in high cognitive load con-
ditions and that its latency could be highly variable
from one subject to another. Based on this observa-
tion we have proposed a new algorithm for adaptive
spatial filtering and time window selection based on
xDAWN algorithm. Classification results have shown
that our algorithm performs better than the xDAWN
algorithm and than classification on raw data with an
improvement up to 17% for correct trials (which is the
most important one as we have said before). Thus,
we have developped a new algorithm that allows our
classifier to adapt to ErrP latency variability. This
is of great interest given its high inter-subject vari-
ability. Moreover it is known that ErrP characteris-
tics may vary with experimental and environmental
conditions. ErrP latency could then evolve within an
experiment, using an adaptive filtering method (that
would be updated along the experiment) would allow
consistent classification results along time. In con-
clusion we have shown that using adaptive filters for
ErrP single trial detection could significantly improve
classification results. Moreover we have developped
a new algorithm that could tackle the problem of ErrP
latency variability. Further studies should be done in
this way, as for example to adapt to latency variability
between trials or maybe to find otpimal time windows
for the different ErrP peaks (since it is known that the
ErrP is characterized by a negative peak and a positive
one).
ACKNOWLEDGEMENTS
We are grateful to Dr. Bertrand Rivet for making us
available the code of his xDAWN algorithm and ex-
plaining us his method. We are grateful to the project
ANR OpenVibe.
REFERENCES
Chavarriaga, R. and Mill
´
an, J. (2010). Learning from eeg
error-related potentials in noninvasive brain-computer
interfaces. IEEE Trans Neural Syst Rehabil Eng,
18(4):381–388.
Comon, P. and Jutten, C. (2010). Handbook of Blind Source
Separation: Independent component analysis and ap-
plications. Academic Press.
Dal Seno, B., Matteucci, M., and Mainardi, L. (2010). nline
detection of p300 and error potentials in a bci speller.
O. Computational intelligence and neuroscience.
Falkenstein, M., Hohnsbein, J., Hoormann, J., and Blanke,
L. (1991). Effects of crossmodal divided attention on
late erp components.ii. error processing in choice re-
action tasks. Electroencephalogr. Clin. Neurophysiol.,
78:447–455.
Ferrez, P. and Mill´an, J. (2005). You are wrong! auto-
matic detection of interaction errors from brain waves.
In Proceedings of the 19th International Joint Confer-
ence on Artificial Intelligence.
Ferrez, P. and Mill´an, J. (2007). Eeg-based brain-computer
interaction: Improved accuracy by automatic single-
trial error detection. In Proc. NIPS.
Fukunaga, K. (1990). Introduction to statistical pattern
recognition (2nd ed.). Academic Press Professional,
Inc., San Diego, CA, USA.
Gentsch, A., Ullsperger, P., and Ullsperger, M. (2009). Dis-
sociable medial frontal negativities from a common
monitoring system for self-and externally caused fail-
ure of goal achievement. Neuroimage, 47(4):2023–
2030.
Gray, R. M. (2006). Toeplitz and circulant matrices: A re-
view. Foundations and Trends in Communications and
Information Theory, 2(3):155–239.
Hajcak, G., Moser, J., Holroyd, C., and Simons, R. (2007).
It’s worse than you thought: The feedback negativity
and violations of reward prediction in gambling tasks.
Psychophysiology, 44(6):905–912.
MacKay, D. (1992). Bayesian interpolation. Neural com-
putation, 4(3):415–447.
Pfurtscheller, G. (1981). Central beta rhythm during sen-
sorimotor activities in man. Electroencephalography
and clinical Neurophysiology, 51(3):253–264.
Rivet, B., Souloumiac, A., Gibert, G., and Attina, V.
(2008). P300 speller brain-computer interface: En-
hancement of p300 evoked potential by spatial fil-
ters. In Proceedings of the 16th European Signal
Processing Conference (EUSIPCO-2008), EURASIP,
Lausanne, Switzerland.
Steinhauser, M. and Kiesel, A. (2011). Performance moni-
toring and the causal attribution of errors. Cognitive,
Affective, & Behavioral Neuroscience.
Yeung, N., Holroyd, C., and Cohen, J. (2005). Erp corre-
lates of feedback and reward processing in the pres-
ence and absence of response choice. Cerebral Cor-
tex, 15(5):535.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
720