Adaptive Smoothing Applied to fMRI Data

M. Bartés-Serrallonga

, J. M. Serra-Grabulosa

2,3

, A. Adan

2,4

, C. Falcón

3,5

N. Bargalló

and J. Sole´- Casals

Digital Technologies Group, University of Vic, Vic, Spain

Departament de Psiquiatria i Psicobiologia Clínica, Universitat de Barcelona, Barcelona, Spain

Institut d’ Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS), Barcelona, Spain

Institute for Brain, Cognition and Behaviour (IR3C), Barcelona, Spain

CIBER-BBN, Barcelona, Spain

Secció de Neuroradiologia, Servei de Radiologia, Centre de Diagnòstic per la Imatge (CDI),

Hospital Clínic de Barcelona, Barcelona, Spain

Keywords: Adaptive Smoothing, fMRI, Wiener Filter, Smoothing, Gaussian Kernel, Noise.

Abstract: One problem of fMRI images is that they include some noise coming from many other sources like the heart

beat, breathing and head motion artifacts. All these sources degrade the data and can cause wrong results in

the statistical analysis. In order to reduce as much as possible the amount of noise and to improve signal

detection, the fMRI data is spatially smoothed prior to the analysis. The most common and standardized

method to do this task is by using a Gaussian filter. The principal problem of this method is that some

regions may be under-smoothed, while others may be over-smoothed. This is caused by the fact that the

extent of smoothing is chosen independently of the data and is assumed to be equal across the image. To

avoid these problems, we suggest in our work to use an adaptive Wiener filter which smooths the images

adaptively, performing a little smoothing where variance is large and more smoothing where the variance is

small. In general, the results that we obtained with the adaptive filter are better than those obtained with the

Gaussian kernel. In this paper we compare the effects of the smoothing with a Gaussian kernel and with an

adaptive Wiener filter, in order to demonstrate the benefits of the proposed approach.

1 INTRODUCTION

Functional Magnetic Resonance Imaging (fMRI) is a

method to map the brain which does not require any

invasive analysis. This is a very useful technique to

identify brain regions of interest activated by

different types of stimulation or activity and also

during resting state. The indicator used to identify

the local activity is the Blood Oxygenation Level

Dependent (BOLD) contrast, which is based on the

brain oxygenation of the neuronal processes

associated with the experimental tasks. Oxygen and

other nutrients is what neurons need to work. Thus,

when brain neurons are activated, there is a change

in blood flow and oxygenation that causes a change

in the Magnetic Resonance (MR) signal received by

the receiver coils. A major level of oxygen in blood

in a particular area means that there is an increase in

neural activity in this zone and a lower level means

the opposite (D’Esposito et al., 1999).

To obtain the BOLD contrast, the subject under

study lies in the magnet under the influence of a

powerful magnetic field and perform a task or is

exposed to an external stimulus. At the same time, a

large amount of images are acquired using ultra-fast

sequences through magnetic resonance. For some of

these scans the stimulus is present and for some

others the stimulus is absent. The low resolution

brain images of the two cases can then be compared

in order to see which parts of the brain were

activated by the stimulus.

After the experiment has finished, the set of

images is pre-processed and analyzed.

One problem of fMRI data is that includes

contributions from many other sources including the

heart beat, breathing and head motion artifacts,

which can cause wrong results (S.A Huettel. et al.,

2004). In order to reduce as much as possible the

amount of noise and to improve signal detection, the

fMRI data is spatially smoothed prior to the analysis.

677

Bartés-Serrallonga M., M. Serra-Grabulosa J., Adan A., Falcón C., Bargalló N. and Solé-Casals J..

Adaptive Smoothing Applied to fMRI Data.

DOI: 10.5220/0004182306770683

In Proceedings of the 4th International Joint Conference on Computational Intelligence (SSCN-2012), pages 677-683

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

The most common and standardized method to do

this task is by using a Gaussian kernel. The principal

problem of this method is that some regions may be

under-smoothed favoring the presence of false

positives, while others are over-smoothed causing a

loss of information. This problem is due to the fact

that the extent of smoothing is chosen independently

of the data and is assumed to be equal across the

image.

Several studies have proposed approaches which

are different from the Gaussian proposal based on

the same theoretical principles, the extent of

smoothing is choosen independently of the data, fact

that can carry on the problems discussed. Some of

these methods are the prolate spheroidal wave

functions (Lindquist and Wager, 2008), wavelets

(Van DeVille, Blu, and Unser, 2006), Gaussians of

varying width (Poline and Mazoyer,1994; Worsley

et al., 1996) and rotations (Shafie et al.,2003). To

solve these problems and limitations, some authors

have proposes to use adaptive smoothing methods as

the use of the Gaussian Markov random field

specifies (Yue et al., 2010) and Propagation-

separation procedures (Tabelow et al.,2006).

In this report we present an alternative procedure

to denoise the fMRI images that differs from the

ones used in the traditional fMRI analysis. This

method is based on an adaptive Wiener filter which

smooths the images adaptively minimizing the loss

of information caused by the over-smoothing and the

apparition of the false positives when the images are

under-smoothed. In this paper, we compare the

effects of the adaptative smoothing based on the

Wiener filter and the effects of the non adaptative

smoothing of the use of the Gaussian kernel,

combinend in both cases with an Independent

component analysis.

2 MATERIALS AND METHODS

The study was performed in a 3 T MRI scanner

(Magnetom Trio Tim, Siemens Medical Systems,

Germany) at the Diagnostic Imaging Centre at

Hospital Clínic of Barcelona (CDIC) using the

blood-oxygen level-dependent (BOLD) fMRI signal.

Whereas the pre-processing of MR images and

the regression model were performed using SPM8

software (SPM8, Wellcome Department of

Cognitive Neurology, London), the data analysis

was carried out using Group ICA of fMRI Toolbox

(Calhoun et al., 2001). Both pre-processing and

analysis software were run on a Matlab platform

(R2009b version).

2.1 Participants

Forty right-handed healthy undergraduate students

[50% women; age range 18–25, mean (+S.D.) 19.6

(+1.7)] were recruited from the University of

Barcelona. Subjects with chronic disorders, nervous

system disorders or history of mental illness were

excluded, as well as regular drinkers and those on

medication. All participants were non smokers and

low caffeine consumers (< 100mg/day), had

intermediate circadian typology and reported an

undisturbed sleep period of at least 6 h during the

night prior to the fMRI scan sessions.

Caffeine may affect the performance of the task

(Serra-Grabulosa et al., 2010a); Adan and Serra-

Grabulosa, 2010). For this reason the participants

abstained from caffeine intake for a minimum of 12

h and fasted for at least 8 h prior to the first fMRI

session.

The study was approved by the ethics committee

of Hospital Clínic de Barcelona. Written consent

was obtained from all participants, who were

financially rewarded for taking part.

2.2 Experimental Design

The functional magnetic resonance imaging was

obtained using gradient echo sequence single-shot

echo-planar imaging, with the following parameters:

TR (repetition time): 2000 ms, TE (echo time): 40

ms, FOV (field of view): 24 x 24 cm, matrix 128 x

128 pixels, flip angle 90, slice thickness: 2 mm, gap

between sections: 0.6 mm, 36 axial slices per scan.

A total of 243 volumes were purchased, with 46

slices each.

During the acquisition of fMRI, in order to

obtain the BOLD contrast, the subjects performed a

sustained attention and working memory task (CPT-

IP, Continuous Performance Test-Identical Pairs),

which is a modification of the Cornblatt task

(Cornblatt et al., 1989) and a control task. CPT-IP

task was created with the software Presentation

(Neurobehavioral System, USA). All stimuli were

presented to the subjects through glasses specially

designed for use in the scanner.

The CPT-IP task was performed using a block

design. It started with a block of 35 seconds of

accommodation to the scanner, which had a blank

screen that the subject had to stare at. After this first

block, 9 blocks of CPT were alternated with 9

blocks of control (Figure 1). Preceding each block,

subjects received instructions for what to do in the

next block for a duration time of 5 seconds.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

678

Figure 1: Design of the sustained attention task with

alternation between blocks.

Figure 2: The following figure illustrates the design of the

task blocks. The top (A) exemplifies the figures presented

in the CPT blocks. In this example, you should respond

to the stimulus e3. The bottom (B) exemplifies the figures

presented in the control blocks.

Each of the CPT blocks had a total of 27

numbers formed by 4 digits (1 to 9, without

repeating the same figure), so that 23 of the figures

were different and 4 were repeated. The presentation

time of each number was 450 ms and the interval

between the onsets of each of the 27 consecutive

digits was 750 ms. Subjects’ task was to detect the

repeated figures and respond by pressing a button as

quickly as possible (Figure 2A). The position of the

repeated figures was randomized over the blocks

CPT. Concerning the control block, it always had

the same 4 digits (1 2 3 4) and the task of the

subjects was only to stare at it throughout the

presentation (Figure 2B).

2.3 Data Pre-processing

Image pre-processing was performed with SPM8

(http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) as

described in (http://www.fil.ion.ucl.ac.uk/spm/doc/

spm8_manual.pdf). The pre-processing steps were

(1) realigning and unwarping the images to correct

for movement artifacts and related susceptibility

artifacts, (2) coregistration of the anatomical to the

functional images, (3) segmentation and normalizing

of the anatomical image to the standard stereotactic

space (Montreal Neurological Institute), (4)

application of normalization transformation to the

functional images, and (5) smoothing the images

with a 8 mm full-width half maximum (FWHM)

Gaussian filter and with an adaptive Wiener filter in

order to have two groups of the same images with

different types of smoothing to compare them later.

2.4 Adaptive Wiener filtering

This filter is a (non-linear) spatial filter which

operates on the principle of least squares. Imagine

that we have a noisy image M’ of some original

image M and a restored version R. Obviously, what

we intend is to have R as close as possible to the

original image M. One way to know if the image R

is close as the image M is by adding the squares of

all differences:

∑(m

i,j

– r

i,j

)

(1)

where the sum is taken over all pixels of R and M

(which we assume to be of the same size). This sum

can be taken as a measure of the closeness of R to

M. If this value is the minimum the resultant image

of the denoising process will be as close as possible

to the original image. The noisy image M’ can be

written as:

M’ = M +N (2)

where M is the original correct image and N is the

noise which we assume to be zero-mean normally-

distributed.

However, the mean may not be zero. Therefore

we suppose that the mean is m

and the variance in

the mask is σ

We suppose also that the variance of

the noise over the entire image is known to be σ

Then the output value can be calculated as:

+ (g - m

)

(3)

where g is the current value of the pixel in the noisy

image. See Lim, 1990 for details. In practice, we

calculate m

by simply taking the mean of all grey

values under the mask, and σ

by calculating the

variance of all grey values under the mask. We may

not necessarily know the value σ

. So the Matlab

function wiener2 (used to filter the images) which

implements Wiener filtering uses a slight variant of

the above equation:

+ (g - m

)

(4)

+ σ

max {0,σ

–

max {σ

AdaptiveSmoothingAppliedtofMRIData

679

where n is the computed noise variance, and is

calculated by taking the mean of all values of σ

over the entire image. This can be very efficiently

calculated in Matlab.

Figure 3: Regression model proposed to explain, for each

voxel of the functional MRI images, the variability in the

signal along the recorded 243 volumes. Each one of the 10

columns corresponds to one of the input variables in the

regression. The first one corresponds to the attention task

in which the subject has to respond to repeated stimuli.

The second one corresponds to the task of looking at

numbers and the third one to the task of initial rest. The

next 6 columns are the values applied to correct the head

movements in the pre-processing step. The last one

represents the error. On the right side of the table the

registered volumes are listed from 1 to 243. For each

variable, white colour indicates that this helps to explain

the variability while black colour indicates the opposite.

2.5 Implementation of the Regression

Model

After the pre-processing step, we proceeded to

perform the regression model to explain brain

activations. To do this, we created a regression line

where signal changes observed in each voxel could

be explained by changes in the proposed task

minimizing the residual error (Figure 3).

2.6 Independent Component Analysis

After pre-processing and regression model creation

steps, we applied ICA analysis in both types of the

smoothed images. What we intend with this analysis

is to check that the components obtained with the

Wiener filter have a time course more similar to the

task pattern than the time course obtained with the

Gaussian kernel (see Figure 4).

Figure 4: Task pattern followed during the CPT task.

To perform the ICA analysis we used the Group

ICA of fMRI Toolbox. This program has the option

to make the analysis using different algorithms, as

Jade, Erica, Infomax, Simbec, Amuse and others.

The chosen algorithm to analyze fMRI data was

Infomax because it has been one of the most

commonly used algorithms for fMRI data analysis

and has proven to be quite reliable (Calhoun et al.,

2004).

3 RESULTS

3.1 Selection of the Independent

Components

After ICA analysis we selected some of the

components in order to evaluate results. For that, we

did a multiple regression and a statistic correlation

with every paradigm. We excluded the components

that had a p-value greater than 0.01, and the ones

which were associated to noise. Therefore we

selected 3 components for the CPT task coming

from every approach.

3.2 Obtention of the Areas of Interest

After the selection of the independent components,

we performed a T – test with all the subjects and all

the components. We also performed a ‘multiple

regression’ SPM8 analysis to establish the

relationship between CPT-IP-related activations.

The fMRI results were interpreted only if they

attained both a voxelwise threshold p<0.05

(corrected) (cluster extent (k) = 10voxels). The

anatomical location of the activated brain areas was

determined by the Montreal Neurological Institute

(MNI) coordinates. Anatomical labels were given on

the basis of anatomical parcellation developed by

(Tzourio-Mazoyer et al., 2002).

3.3 Results with the Different

Smoothing Methods

In the following images taken from one sample, we

can see the results obtained with every smoothing

method. The first image (Figure 5) is an example of

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

680

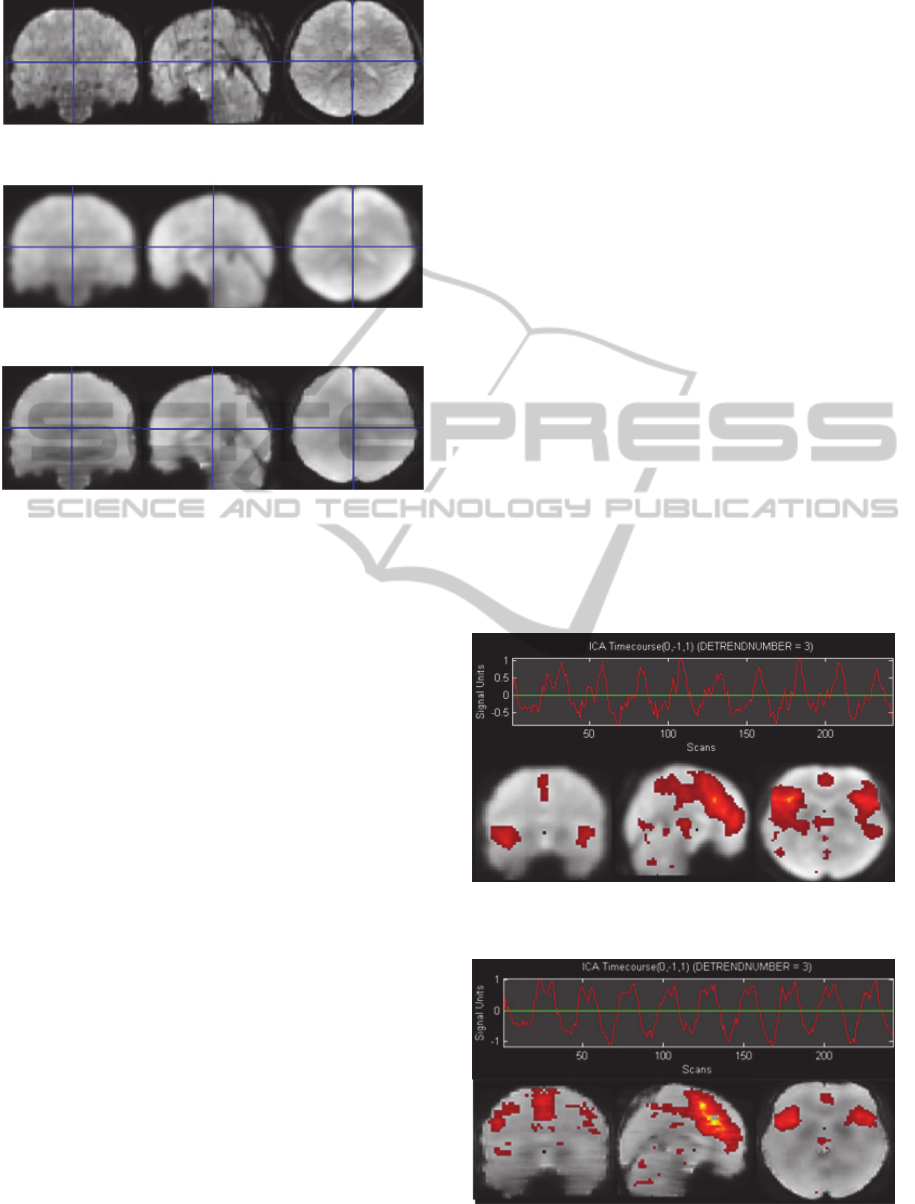
Figure 5: fMRI image without smoothing.

Figure 6: fMRI image smoothed with a Gaussian kernel.

Figure 7: fMRI image smoothed with an adaptive Wiener

filter.

a non smoothed image with noise. The next two

images (Figures 6 and 7) correspond to the same

image smoothed with the two mentioned methods.

As we have mentioned before, we applied an

ICA analysis on all the subjects in order to check the

components obtained with every method, as is

illustrated in the next images.

Activations found in the CPT task with the

Wiener filter were located bilaterally in frontal lobe

(BAs Left 4, 6, 8, 9, 10, 32, right 45, right 46, 47),

parietal (BAs 7, 39, 40), temporal (BAs Left 22, 37)

and occipital (BAs Left 17, 18, 19).

Activations found in the CPT task with the

Gaussian kernel were located bilaterally in frontal

lobe (BAs 4, 6, 8, 9, right 10, right 32, 45, 46, 47),

parietal (BAs right 2, Left 5, 7, 31, Left 39, 40, Left

41), temporal (BAs Left 20, 21, 22, Left 37) and

occipital (BAs Left 17, 18, 19).

4 DISCUSSION

This paper introduces an approach to smooth fMRI

data based on the use of an adaptive Wiener filter.

The results from the proposed method were

compared with those obtained through the

conventionally used Gaussian smoothing.

The principal feature of our approach respect to

the classic methods is that it allows varying the

extent of smoothing across the brain. This

characteristic will help to avoid the problems related

with over and under-smoothing that may occur if

smoothing is performed using a Gaussian kernel of

fixed width. In the following paragraphs we will

comment these problems with the achieved results.

If we take a look at the figures (Figures 5, 6 and

7), we can observe that in figure 6 the edges of the

images are fuzzy and have less resolution than the

images in the figure 7. This fact indicates that the

images in the figure 6 are over-smoothed causing

probably a loss of information. On the other hand,

the images of the figure 7 have more definition and

the edges have been preserved after the smoothing

process because the adaptive Wiener filter smooths

an image adaptively, tailoring itself to the local

image variance. Where the variance is large,

performs little smoothing. Where the variance is

small, performs more smoothing. As a result this

filter is more selective than the Gaussian kernel and

preserves better the edges and other high-frequency

parts of the image.

If we compare the time courses and the

activations maps between the components achieved

with the Gaussian kernel and the adaptive filter we

can see that all of them are very similar except the

ones presented in the figures 8 and 9.

Figure 8: Component from the CPT task obtained with the

Gaussian kernel.

Figure 9: Component from the CPT task obtained with the

adaptive Wiener filter.

AdaptiveSmoothingAppliedtofMRIData

681

If we take a look to the activations found, we can

see that the adaptive filter found less active regions.

These correspond to the zones parietal (BAs 2, 5, 3,

41) and temporal (BAs 20, 21) which are basically

present in the figures 8 and 10.

Between all of these areas, the ones which

probably could be activated by the task are the BA 5

which is related with the working memory (Yoo et

Al., 2004) and BA 20 which is associated with the

dual working memory task processing (Yoo et Al.,

2004).

However, if we look previous studies (Bartés et

al. 2011) which studied the same task using ICA, we

can see that the BAs 5 and 20 were not found. By

this fact and because the figure 8 has more abrupt

changes in the time course than the figure 9 which

differs a little bit from the task pattern, we believe

that the components of the figures 8 and 10 have

some false positives which are removed by the

adaptive Wiener filter in the figures 9 and 11.

Figure 10: Component from the CPT task obtained with

the Gaussian kernel.

Figure 11: Component from the CPT task obtained with

the adaptive Wiener filter.

5 CONCLUSIONS

We have compared the effects of two different

denoising approaches: the use of Gaussian kernel

and the use of an adaptive Wiener filter. After the

analysis, the adaptive Wiener filter demonstrated to

be a technique with a great potential. Comparing

with the fixed Gaussian approache, is able to remove

the noise minimizing the over/under-smoothing. The

results provided evidences to state that the Gaussian

kernels alter the spatial shape and extent of the

activation regions, when applied for denoising fMRI

data. Therefore, we believe that the approach

proposed in this paper could be a good alternative to

the classic smoothing methods.

Figure 12: Component from the CPT task obtained with

the Gaussian kernel.

Figure 13: Component from the CPT task obtained with

the adaptive Wiener filter.

ACKNOWLEDGEMENTS

This work has been partially supported by the

Secretaria d’Universitats i Recerca of the

Departament d’Economia i Coneixement of the

Generalitat de Catalunya under the grant 2010BE1-

00772 to Dr. Jordi Solé-Casals; by the University of

Vic under de grant R0904; and by grants of the

Ministerio de Educación y Ciencia of the Spanish

Government (SEJ2005-08704) and the Departament

d’Innovació, Universitats i Empresa of the

Generalitat de Catalunya /2009BE-2 00239) to Dr.

Josep M Serra-Grabulosa.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

682

REFERENCES

Adan, A., Serra-Grabulosa, J.M., 2010. Effects of caffeine

and glucose, alone and combined, on cognitive

performance. Human Psychopharmacology clinical

and experimental, 25 (4), 310 – 317.

Bartés-Serrallonga, M., Solé-Casals, J., Adan, A., Falcon

C., Bargallo, N., and Serra-Grabulosa, J. M., 2011.

Statistical analysis of functional MRI data using

independent component analysis. International

conference on neural computation theory and

applications. 430 – 436.

Calhoun, V. D., Adali, T., Pearlson, G. D. and Pekar, J. J.,

2001. A Method for Making Group Inferences From

Functional MRI Data Using Independent Component

Analysis. Human Brain Mapping, 14, 140 – 151.

Calhoun, V. D., Adali, T., Pearlson,G. D., 2004.

Independent component analysis applied to fMRI data:

a generative model for validating results. The Journal

of VLSI Signal Processing, 37, 281 – 291.

Cornblatt, B.A., Lezenweger, M.F., Erlenmeyer-Kimling,

L., 1989. The Continuous Performance Test, Identical

Pairs Version: II. Contrasting attentional profiles in

schizophrenic and depressed patients. Psychiatry

Research, 29, 65 – 85.

D’Esposito, M., Zarahn, E., Aguirre, G. K., 1999. Event-

Related functional MRI: implications for cognitive

Psychology. Psychological Bulletin, 125, 155 – 64.

Lim, J. S., 1990. Two-Dimensional Signal and Image

Processing. Prentice Hall.

Lindquist, M. and Wager, T., 2008. Spatial smoothing in

fmri using prolate spheroidal wave functions. Human

Brain mapping, 29, 1276 – 1287.

Poline, J. and Mazoyer, B. 1994. Analysis of individual

brain activation maps using hierarchical description

and multiscale detection. IEEE Transactions in

Medical Imaging, 4, 702 – 710.

Serra-Grabulosa J. M, Adan A, Falcon C, Bargallo N,

2010a Glucose and caffeine effects on sustained

attention: an exploratory fMRI study. Human

Psychopharmacology clinical and experimental 25 (7-

8), 543 – 552

Shafie, K., Sigal, B., Siegmund, D., and Worsley, K.,

2003. Rotation space random fields with an

application to fmri data. Annals of Statistics, 31, 1732

– 1771.

Tabelow, K., Polzehl, J., Voss, H. U., Spokoiny, V., 2006.

Analyzing fMRI experiments with structural adaptive

smoothing procedures. NeuroImage, 33, 55 –62.

Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D.,

Crivello, F., Etard, O., Delcroix, N., Mazoyer, B. and

Joliot, M., 2002. Automated anatomical labeling of

activations in SPM using a macroscopic anatomical

parcellation of the MNI MRI single-subject brain.

Neuroimage 15, 273 – 289.

Van De Ville, D., Blu, T., and Unser, M., 2006. Surfing

the brain: An overview of wavelet-based techniques

for fmri data analysis. IEEE Engineering in Medicine

and Biology Magazine, 25, 65 – 78. .

Worsley, K. J., Marrett, S., Neelin, P., Vandal, A. C.,

Friston, K. J., and Evans, A. C., 1996. A unified

statistical approach for determining significant signals

in images of cerebral activation. Human Brain

Mapping, 4, 58 – 73.

Yoo, S. S., Paralkar, G., Panych, L. P., 2004. Neural

substrates associated with the concurrent performance

of dual working memory tasks. The international

journal of neuroscience. 114(6), 613 – 31.

Yue, Y., Loh, J.M., Lindquist, M.A., 2010. Adaptive

spatial smoothing of fMRI images. Statistics and Its

Interface, 3, 3 – 13.

AdaptiveSmoothingAppliedtofMRIData

683