FPGA Implementation of SOBI to Perform BSS in Real Time

Apurva Rathi

1,2

, Xun Zhang

and Francois Vialatte

VIT University, Vellore, India

ISEP, Paris, France

ESPCI, Paris, France

Keywords: EEG, BSS, SOBI, FPGA.

Abstract: Blind Source Separation (BSS) is an effective and powerful tool for source separation and artifact removal

in EEG signals. For the real time applications such as Brain Computer Interface (BCI) or clinical Neuro-

monitoring, it is of prime importance that BSS is effectively performed in real time. The motivation to

implement BSS in Field Programmable Gate Array (FPGA) comes from the hypothesis that the

performance of the system could be significantly improved in terms of speed considering the optimal

parallelism environment that hardware provides. In this paper, FPGA is used to implement the SOBI

algorithm of EEG with a fixed-point algorithm. The results obtained show that, FPGA implementation of

SOBI reduces the computation time and thus has great potential for real time.

1 INTRODUCTION

EEG is one of the most widespread brain mapping

techniques to date and is used extensively for

monitoring the electrical activity within the human

brain both for research and clinical purposes. The

raw EEG data represent a projection of a set of

signals, which are a mix of brain and artifact

information. BSS is the process of recovering the

source signals from a linear mixture of measured

signals.

There is no general consensus about any one

BSS Algorithm being the best. Each algorithm has

its unique set of pros and cons and makes certain

assumptions about the sources in order to

compensate for the lack of information about the

mixing matrix and to be able to process the signals

blindly. (Joyce et al., 2004; Fitzgibbon et al., 2007)

and (Hyvarinen et al.) can serve as good reads for

literature on Artifact detection and removal in EEG

signals. SOBI using time structure of signals has its

unique set of advantages to offer as mentioned in

(Delorme et al., 2007) and was the chosen algorithm

in this work.

SOBI assumes stationary sources with non-

identical spectra and considers components at

various time lags and focuses on decorrelating them

as much as possible. As mentioned earlier, SOBI

offers some unique advantages such as ability to

resolve correlated signals, ability to resolve more

than one gaussian sources, more robust behaviour in

adverse Signal to Noise ratio (SNR), need for fewer

data points implying shorter epoch length –

something which is must for real time processing.

The application and usefulness of SOBI in Brain

Computer Interface has been shown in (Wang et al.).

It was shown that SOBI converges after only a few

iterations thus proving it worthy for real time

applications. However, the computational

complexity and cost for SOBI is high which can be

partially taken care of by appropriate design of the

FPGA architecture. Also, when real time processing

is the main goal a little additional cost is justifiable.

In this paper, an FPGA implementation of the

SOBI algorithm of BSS model is presented with co-

simulation design concept based on the fixed-point

number representation. The BSS Model and SOBI

algorithm are introduced in Section 2. In section 3,

the FPGA implementation is described. The result

analysis and the conclusion are given in section 4

and 5.

727

Rathi A., Zhang X. and Vialatte F..

FPGA Implementation of SOBI to Perform BSS in Real Time.

DOI: 10.5220/0004182507270731

In Proceedings of the 4th International Joint Conference on Computational Intelligence (SSCN-2012), pages 727-731

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 ALGORITHM AND PROBLEM

FORMULATION

2.1 BSS Model

BSS is the process of recovering the source

signalsfrom a linear mixture of measured signals.

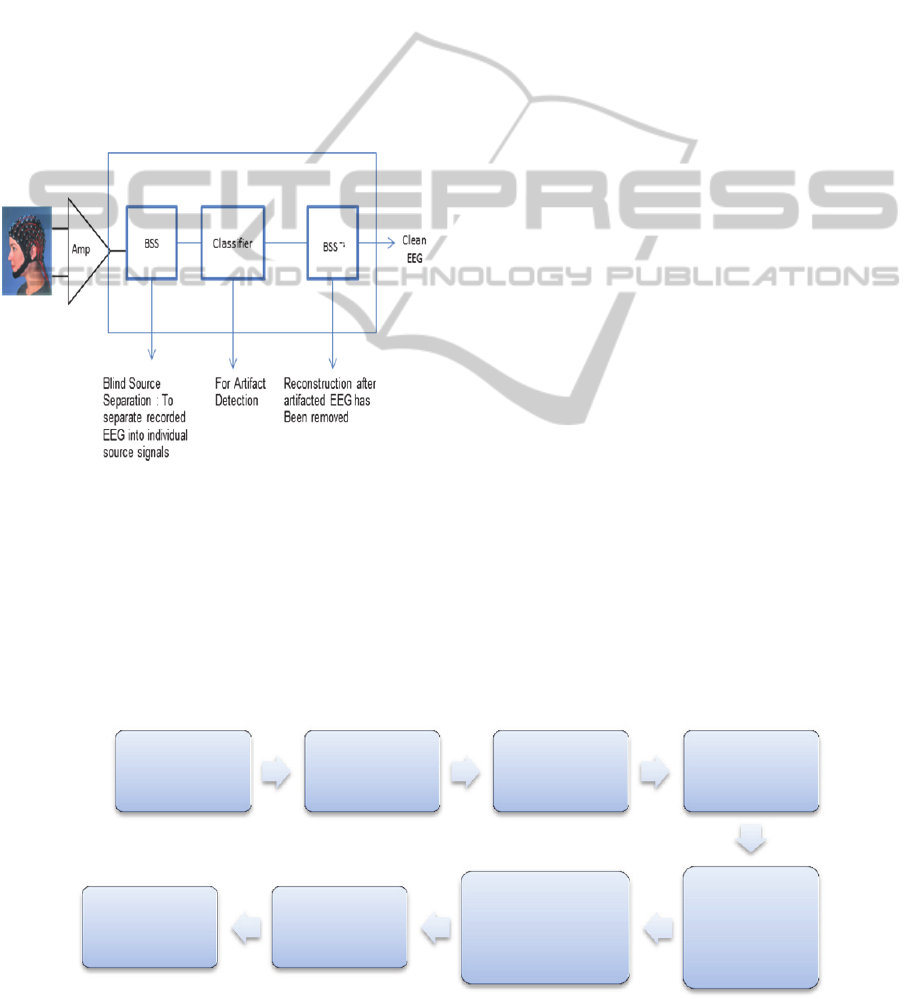
There are three distinct steps required for removal of

artifact/noise from EEG using BSS: 1) separate

(unmix) the measured EEG into sources using a BSS

algorithm, 2) identify and discard artifact/noise

sources and retain brain sources, and 3) project the

retained brain sources back into sensor space

resulting in artifact/noise-free EEG as is illustrated

in Fig. 1

Figure 1: Artifact detection and removal using BSS.

Component estimation from EEG data can be

mathematically formulated as follows.

X = AS (1)

meaning that the sensor data X is rotated by an

unmixing matrix 



, to arrive at the components S.

To clarify, all quantities in Equation 1 are matrices.

A is referred to as the mixing matrix, each column of

which describes signal propagation from an

individual source to each electrode site. The

meaning of “blind” is that both the original sources

(represented by matrix S) and the way the sources

were mixed (represented by A) are all unknown, and

only mixed signals or mixtures represented by X)

can be measured and observed.

2.2 SOBI Algorithm

SOBI was first introduced by Adel Belouchrani,

Karim Abed-Meraim, Jean François Cardoso and

Eric Moulins in the year 1997. The steps involved in

SOBI algorithm are illustrated in Figure 2 while the

detail explanation of the algorithm may be found in

(Belouchrani et al., 1997). As previously stated,

SOBI exploits the time coherence of the source

signals for source separation. As opposed to the

other approaches, it relies only on stationary second

order statistics. It was shown in (Tong et al., 1990;

Belouchrani et al., 1993) that blind identification is

feasible based on the eigen decomposition of spatial

covariance matrices. In (Belouchrani et al., 1997),

blind identification is achieved by performing joint

diagonalization of a set of spatial covariance

matrices. In (Belouchrani et al., 1997) it was also

shown that considering a set of matrices rather than

unique correlation matrix increases the robustness at

a low additional computing cost. SOBI exploits the

time coherence of the source signals and assumes

that the signals are uncorrelated in time. Also, for

the sake of simplicity the noise is modelled as

additive white noise. However, this assumption is

not crucial. The aim of BSS is to identify the

mixture matrix A and to recover the source signals s

(t) from the array output x (t) without any a priori

knowledge of the array manifold.

Figure 2: Schematic Representation of BSS using SOBI.

Filter Buffer Normalizer Whitening

Calculate

theCorrelation

Matrices

Joint

Diagonalization

Estimating

SourceSignals

PostProcessing

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

728

The first pre-processing step is Normalization so

as to ensure that the source signals have unit

variance. The next step is Whitening which is

achieved by Singular Value Decomposition of the

mixture matrices. Whitening reduces the

dimensionality of the BSS problem, following which

the mixing matrix A may be defined as

A = 

U (2)

Where W is the whitening matrix and U is a unitary

matrix. It is shown in (Belouchrani et al., 1997) that

the whitening matrix is determined from covariance

matrix at t = 0 (R (0)), provided the noise covariance

matrix is known or can be estimated. The Unitary

factor U may be thought of as a unitary matrix that

simultaneously diagonalizes a set of covariance

matrices considered at various time lags. A detailed

analysis of SOBI algorithm can be found in

(Belouchrani et al., 1997). Though SOBI has not

been implemented in hardware before, (Huang et al.,

2008; Shyu et al., 2008; Li and Lin, 2005 and Du

and Qi, 2004) can be good references for literature

on hardware implementation of other BSS

algorithms.

3 DESIGN AND

IMPLEMENTATION

3.1 Design Methodology

Fig 2 illustrates the basic flow of the SOBI

Algorithm. As is evident, Whitening i.e. Singular

Value Decomposition, Correlation i.e. determining

the correlation matrices and Joint Diagonalization of

the correlation matrices; comprise of the major part

of the algorithm. Firstly, a SIMULINK model was

developed and the results were compared to those

obtained from the MATLAB code. The SIMULINK

model was built in order to be able to perform

Hardware Co-simulation, which is an intermediate

stage between software and hardware

implementation. This intermediate approach is

expected to gauge the benefits of both software and

hardware and thus could provide a better solution.

This is based on the belief that it is not always

prudent and economical to implement the entire

system in hardware. Instead, implementing only

those blocks which allow certain amount of

parallelism and / or for which the computational

time is to be reduced, could turn out to be more

economical and better solution.

The three approaches to develop a Co-simulation

between SIMULINK/ MATLAB and XILINX ISE

are as mentioned below:

1) Using System Generator

2) Using HDL Coder and EDA Simulator Link

3) Using EDA Simulator Link and a Black Box

containing the hand coded VHDL code.

In the first two approaches, the VHDL code is

automatically generated from a MATLAB code or a

SIMULINK model. However, there are several

restrictions on what all MATLAB functions can be

directly mapped onto a VHDL code. In view of

these limitations and after several failed attempts

with the first two approaches, it was decided to hand

code the VHDL code. Also, hand coded VHDL code

offers the advantage that it can be optimized as per

the need.

Thus, VHDL code for three of the most

important blocks – Singular Value Decomposition,

Correlation and Joint Diagonalization - of the SOBI

model were written and simulation results were

obtained for the same. The next step was to

synthesize the blocks. The code for which

simulation results were obtained was written using

real data type, which is not synthesizable. Thus, the

code for Correlation block was rewritten using

Floating point representation and simulation results

were obtained for the same. However, as the floating

point package (Bishop, 2005), (that need to be used

since floating point was not an inbuilt data type until

VHDL 2008) integrated in VHDL 2008 is not yet

officially supported by Xilinx XST13.4, several

synthesis issues were encountered. Thus, the

correlation Block was finally synthesized using

signed number representation. Finally, the synthesis

report was generated and the parameters were

modified so as to optimize the performance.

3.2 Proposed Architecture for

Correlation Block

The Figure 3 denoted below represents the process

to determine a single Correlation matrix. n such

processes may be run in parallel to determine the n

correlation matrices at various time lags. However,

running the processes in parallel would imply more

hardware resources being used.

FPGAImplementationofSOBItoPerformBSSinRealTime

729

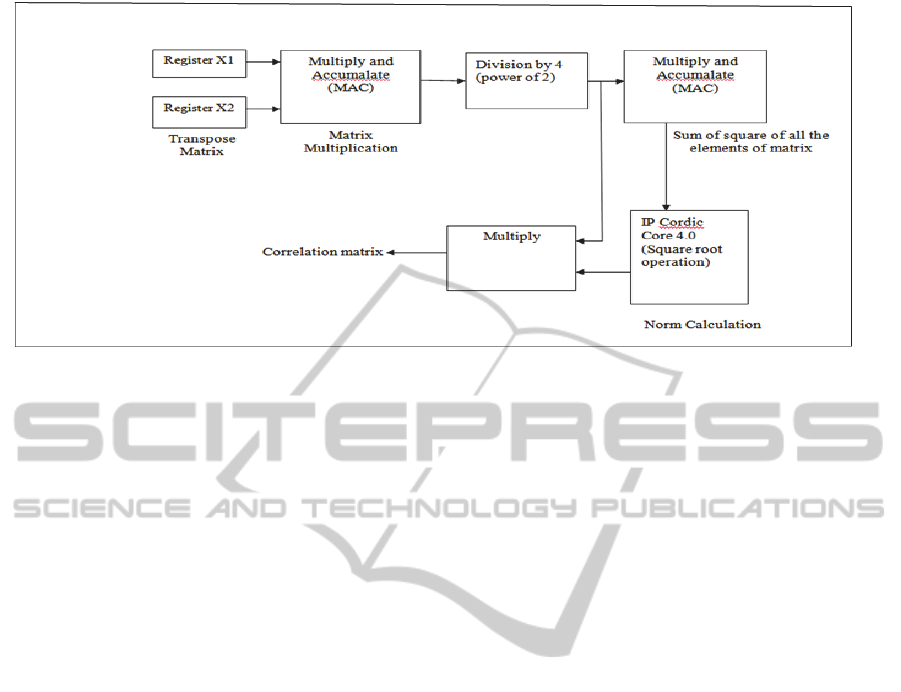
Figure 3: Proposed architecture for implementation of Correlation Block.

4 RESULTS

4.1 Simulation Results

As mentioned earlier, the simulation results for SVD

block (using real data type), correlation Block (using

real, floating point and signed numbers data type)

and Joint Diagonalization block (using real and

floating point data type) were obtained considering a

2 x 4 input matrix, that is, 2 channels and 4 data

points. The parameter p which determines the

number of correlation matrices to be considered, was

set to 2. Several observations were made which are

listed below.

If it is intended to write a synthesizable code, real

data type should not be used. The use of Logic cores

to implement mathematical functions such as square

root, does introduce a bit of latency and thus some

hand coded functions should be developed instead.

Also, though it is easy to program in Floating Point

it is certainly not a hardware Engineer’s choice as it

utilizes a lot of hardware resources.

Both the Joint Diagonalization and SVD block

involved the calculation of eigen values and vectors.

Based on the simulation results, it was concluded

that the power method should be used only when the

largest eigen value and the corresponding eigen

vector is to be calculated. While it worked well in

the Joint Diagonalization block, it didn’t produce

accurate results for the SVD block which involved

calculation of eigen values and vectors of a 2 x 2

matrix. Thus, the Jacobi method should be used

instead.

4.2 Synthesis Results

Using the signed integer data type, the synthesis of

the correlation block was made possible and the

synthesis report was generated. The mapping

procedure failed due to the over utilization of IOBs

(Bounded input output). However, the synthesis

report generated does provide some insight into the

synthesis of the code. The timing report shows a

minimum delay of 12.795 ns which corresponds to a

Maximum frequency of 78.155 Mhz. This is higher

than the maximum frequency of 64 MHz achieved in

(Huang et al., 2008). Although, in (Huang et al.,

2008) the entire algorithm was implemented while in

our case only a part of it is implemented. As

observed by changing a few parameters, it may be

concluded that there is a lot of scope for

optimization.

5 CONCLUSIONS

Thus, the synthesis results obtained for the

Correlation Block, do verify that the computation

time could be reduced by implementing the SOBI

algorithm in FPGA. Also, there is scope for a lot of

optimization that can be done to achieve higher

speed. Also, as was observed while working on the

codes, SOBI does offer a lot of scope for parallelism

and pipelining as there are a lot of matrix operations

involved and thus it seems only wise to implement it

in FPGA. Once, the major blocks of Correlation,

Joint Diagonalization and Singular Value

Decomposition are made synthesizable, it might be

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

730

interesting to perform Co-simulation between

MATLAB - Xilinx and make a comparison between

Software, Hardware and Hardware Co-simulation.

Based on the results, it can be decided as to what

actually to implement in FPGA. This way an

economical use of Hardware resources can be made.

In the near future, when the floating and fixed point

packages are officially supported by Xilinx XST for

synthesis purpose, the same work can be

implemented using Fixed or Floating point

representation, which unlike integers is a descent

way of representing real life EEG data.

This work is the first initiative taken to

implement SOBI to perform BSS in Real time and

thus is just at a preliminary stage. The project

provides a global view of the implementation, while

considering the Correlation block in-depth. This

work could be used to make a choice of the methods

to implement various blocks, as an analysis of the

methods for each block has been made in this

project. A lot of work needs to be done further.

However, the work does provide hope that SOBI

could serve as a potential candidate for real time

BSS. Thus, it could pave a way for on-line

processing required in applications like Brain

Computer Interface.

ACKNOWLEDGEMENTS

SIGMA Laboratory, ESPCI, Paris Tech

ISEP, Paris

Gerard Drefus, ESPCI, Paris

Yohei Tomita, SIGMA Lab, ESPCI, Paris

Parvaneh Adibpour, SIGMA Lab, ESPCI, Paris

Antoine Gaume, SIGMA Lab, ESPCI, Paris

REFERENCES

Carrie A. Joyce, A Irina F. Gorodnitsky, B And Marta

Kutasb,c, “Automatic removal of eye movement and

blink artifacts from EEG data using blind component

separation”, Psychophysiology, 41 (2004)

S. P. Fitzgibbon,* D. M. W. Powers,† K. J. Pope,† C. R.

Clark*, “Removal of EEG Noise and Artifact Using

Blind Source Separation”, J Clin Neurophysiol. 2007

Jun;24(3):232-43.

A textbook by Aapo Hyvarinen, Juha Karhunen, Erki Oja,

“Independent Component Analysis”

Arnaud Delorme1,2, Terrence Sejnowski1, Scott Makeig2,

“Enhanced detection of artifacts in EEG data using

higher-order statistics and independent component

analysis”, NeuroImage 34 (2007) 1443–1449

Yan Wang1, Matthew T. Sutherland2, Lori L.

Sanfratello2, Akaysha C. Tang234, “Single-Trial

Classification Of Erps Using Second-Order Blind

Identification (Sobi)”,

Wei-Chung Huang1, Shao-Hang Hung1, Jen-Feng

Chung1,2, Meng-Hsiu Chang1, Lan-Da Van2, and

Chin-Teng Lin1,2, “FPGA Implementation of 4-

Channel ICA for On-line EEG Signal Separation”,

Biomedical Circuits and Systems conference, 2008.

BIOCAS.2008.IEEE

Kuo-Kai Shyu, Member, IEEE, Ming-Huan Lee, Yu-Te

Wu, and Po-Lei Lee, “Implementation of Pipelined

FastICA on FPGA for Real-Time Blind Source

Separation”, IEEE Transactions on Neural Networks,

vol. 19, No. 6, June 2008

Zhongfeng Li and Qiuhua Lin, “FPGA Implementation of

Infomax BSS Algorithm with Fixed-Point Number

Representation ”, Neural Networks and Brain, 2005.

ICNN&B ’05 An International Conference on 13 – 15

Oct. 2005

Hongtao Du and Hairong Qi, “An FPGA Implementation

of Parallel ICA for Dimensionality Reduction in

Hyperspectral Images”, Geoscience and Remote

Sensing Symposium, 2004. IGARSS ’04 . Proceedings.

2004 IEEE International

L. Tong, V. C. Soon, R. Liu, and Y. Huang, “AMUSE: A

new blind identification algorithm,” in Proc. ISCAS,

New Orleans, LA, 1990.

A. Belouchrani, K. Abed Meraim, J.-F. Cardoso, and E.

Moulines, “Second-order blind separation of

correlated sources,” in Proc. Int. Conf. Digital Signal

Processing, Cyprus, 1993, pp. 346–351.

Adel Belouchrani, Member, IEEE, Karim Abed-Meraim,

Jean-François Cardoso, Member, IEEE and Eric

Moulines, Member, IEEE, “A Blind Source

Separation Technique Using Second-Order Statistics”,

IEEE Transactions on Signal Processing, vol. 45, no.

2, February 1997

David Bishop, “Fixed and Floating Point packages for

VHDL”, http://www.vhdl.org/fphdl/Float_ug.pdf

FPGAImplementationofSOBItoPerformBSSinRealTime

731