
On the Applicability of the Notion of Entropy
for Business Process Analysis
Peter De Bruyn, Philip Huysmans, Gilles Oorts and Herwig Mannaert
Normalized Systems Institute
Department of Management Information Systems, University of Antwerp, Prinsstraat 13, 2000 Antwerp, Belgium
{peter.debruyn, philip.huysmans, gilles.oorts, herwig.mannaert}@ua.ac.be
Keywords:
Entropy, Business Process Analysis, Normalized Systems.
Abstract:
Contemporary organizations need to be able to dynamically adapt, improve and analyze their business pro-
cesses. While many approaches are available in literature, few of them tend to use typical engineering concepts
for this purpose. In this paper, we employ the concept of entropy as defined in statistical thermodynamics to
advance the field of business process analysis. After reviewing some existing literature on entropy and its
application in business topics, we show how earlier insights from entropy reasoning in Normalized Systems
theory may offer opportunities to be applied in business process engineering as well. The necessary entropy
concepts are defined in a business process context, entropy occurence in business processes is illustrated and
some initial principles for controlling the resulting entropy are discussed. Finally, some implications for both
theory and practice (e.g., Service-Oriented Architectures) are reviewed.
1 INTRODUCTION
In current business environments, organizations are
increasingly confronted with more demanding cus-
tomers and fiercer competitors forcing them to con-
tinuously change and adapt their business plans, prod-
ucts, services and business processes. Consequently,
a lot of research on the improvement, optimization and
change of business processes has been performed re-
cently. Typical variations of terms referring to this
issue include Business Process Reengineering (BPR),
Core process redesign, process innovation, business
process transformation, organizational reengineering,
Total Quality Management (TQM), etcetera (O’Neill
& Sohal, 1999). Many of those approaches mainly
provide overall project management related best prac-
tices and life cycles such as “secure management
commitment”, “discover process opportunities” and
“inform stakeholders” (Kettinger, Guha & J.T.C.,
1995) or general optimization techniques such as
“have those who use the output of the process per-
form the process” and “link parallel activities instead
of integrating their results” (Hammer, 1990). Such
general guidelines have clearly proven their value in
the past. However, while often claiming terms as “de-
sign” and “engineering”, it is remarkable to note how
few approaches actually apply traditional engineering
concepts as the core of their method to optimize or
change the considered business processes.
Hence, in this paper we will try to advance the
field of business process analysis by applying the en-
tropy concept from thermodynamics for this purpose.
We will do so by applying the theoretical framework
of Normalized Systems (NS). NS is an approach to de-
sign evolvable modular structures, based on theoret-
ically proven theorems. While it was originally ap-
plied at the level of software architectures (Mannaert,
Verelst & Ven, 2011, 2012), its relevance at the orga-
nizational level has already been demonstrated previ-
ously (Van Nuffel, 2011; Huysmans, 2011). However,
the NS theorems were initially proven and derived
from the concept of stability as defined in systems
theory. Recently, the existing theorems have been
confirmed by reasoning based on the concept of en-
tropy while simultaneously suggesting new insights
(and two new theorems) at the software architecture
level (Mannaert, De Bruyn & Verelst, 2012). Conse-
quently, we will try to make an initial attempt in this
paper to verify whether it is valuable to analyze busi-
ness processes from the NS entropy viewpoint as well
and whether new insights seem to emergecorrespond-
ingly.
The remainder of this paper will be structured as
follows. In Section 2 some related work on the con-
cept of entropy will be discussed, including some pre-
vious attempts to use the concept in management and
128
De Bruyn P., Huysmans P., Oorts G. and Mannaert H.
On the Applicability of the Notion of Entropy for Business Process Analysis.
DOI: 10.5220/0004461901280137
In Proceedings of the Second International Symposium on Business Modeling and Software Design (BMSD 2012), pages 128-137
ISBN: 978-989-8565-26-6
Copyright
c
2012 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

organizationalresearch. Next, we will briefly summa-
rize the essence of Normalized Systems theory in Sec-
tion 3 and its extension based on entropy. Section 4
will discuss the usefulness of analyzing business pro-
cesses from the NS entropy viewpoint, whereas Sec-
tion 5 will deal with some of the resulting implica-
tions for theory and practice. Finally, some conclu-
sions will be presented in Section 6.
2 RELATED WORK ON
ENTROPY
In this section we will first provide some definitions
and context regarding the concept of entropy. Next,
we will discuss some earlier attempts of applying en-
tropy reasoning to business and management topics.
2.1 Basic Concepts
Entropy, referring to the second law of thermodynam-
ics, is generally considered to be a fundamental prop-
erty in engineering sciences. The concept has been
described and studied from many different perspec-
tives, but all have basically the intention of describing
the irreversibility of nature. Typically, more specific
interpretations associated with entropy include (1)
complexity, perceived chaos or disorder (Anderson,
2005), (2) uncertainty or lack of information (Shan-
non, 1948) and (3) the tendency of constituent parti-
cles in a system to dissipate or spread out (Leff, 1996).
At one point, most interpretations can be broughtback
to the phenonomen that the modules (or in their most
elementary form: particles) in a system have the nat-
ural tendency to interact (being coupled) in an uncon-
trolled way unless additional structure (i.e, energy or
effort) is introduced in the system.
In this paper — as done previously in NS (Man-
naert et al., 2012) — we will start from the statistical
thermodynamics perspective towards entropy. Here,
it was defined by Boltzmann in 1872 as the num-
ber of possible microstates consistent to the same
macrostate of that system (Boltzmann, 1995). The
macrostate refers to the whole of externally observ-
able and measurable (macroscopic) properties of a
system (typically temperature or pressure of a gas),
whereas the microstate depicts the whole of micro-
scopic properties of the constituent parts of the system
(i.e., modules and particles). Generally, a particular
macrostate (e.g., a certain temperature in a container)
can be obtained by a myriad of different combinations
of microstates (i.e., many different configurations of
the molecules embedded into the container resulting
in the same temperature). The higher the number of
microstates consistent with that macrostate, the larger
the degree of entropy becomes according to statistical
thermodynamics. This relation can also be expressed
in the following formula:
S = k
B
log(W) (1)
where S stands for the amount of entropy regard-
ing a particular macrostate of a system, k
B
equals
the Boltzmann constant and W refers to the possible
number of microstates consistent with the considered
macrostate, given the assumption that each microstate
is equally probable. According to this definition, en-
tropy can then be seen as a measure of the information
(or lack thereof) we have of the system, complying
with the above mentioned interpretations of entropy
as uncertainty or perceived disorder. In terms of the
natural tendency of particles to interact, it can be seen
as if they all “contribute” to the final resulting (ob-
servable) macrostate of the system through their mu-
tual interactions, while it is unclear for the observer
which exact configuration of particles (out of many
possible configurations) brought it into being.
2.2 Entropy Applied in Business Topics
Several attempts have been made in the past to re-
late entropy concepts to business challenges and situ-
ations. Not claiming to be exhaustive or complete, we
will illustrate some of them in this section.
For example, Trienekens, Kusters, Kriek &
Siemons (2009) have elaborated the concept of en-
tropy in the context of software development pro-
cesses. First, they operationalized entropy as the
amount of disorder, lack of structure and ‘instability’
1
apparent in a system, being measured by the com-
plexity (i.e., the number of interacting components)
and change (i.e., the amount of changes over time) in
the system. Also, they made the distinction between
internal and external entropy: the former referring to
the degree of ad-hoc organization inside the organiza-
tion itself, the latter denoting the dynamism of its sur-
rounding environment. As such, they conclude that
both types of entropy are required to be in balance.
Janow (2004) studied the productivity and organi-
zational decision making within firms based on Shan-
non’s entropy approach. In doing so, he found theo-
retical arguments to support the finding that organiza-
tions tend to become slower in their decision making
1
The notion of stability according to Trienekens et al.
(2009) was not formally defined in their article, although
the meaning of invariability (absence of change) seems to
be clearly suggested. This interpretation should not be con-
fused with the definition as proposed by Mannaert et al.
(2011, 2012) and employed in the remainder of this paper,
as both interpretations clearly differ.
On the Applicability of the Notion of Entropy for Business Process Analysis
129

process as well as lose productivity when they grow.
By analogy with the information theory developedfor
communication systems, an organization is consid-
ered as a network consisting of nodes (here: human
beings) taking decisions and communicating them
with each other. Each organization is then proven to
reach “saturation” at a certain organizational size, re-
sulting into organizational trashing and productivity
implosion.
Next, entropy was also considered as being
a measure for the degree of industry concentra-
tion (Horowitz, 1970) or corporate diversification
(Jacquemin & Berry, 1979; Palepu, 1985). Again, the
relation to the uncertainty interpretation of entropy is
made is the sense that highly concentrated industries
are considered to have a higher degree of entropy as
it is more difficult is such situations to predict which
of the several available companies will obtain the ul-
timate preference of a particular consumer.
Finally, the intent of Jung (2008) and Jung, Chin
& Cardoso (2011) of measuring the degree of entropy
present in business process models resulting in some
uncertainty measures of process models, seems to be
most closely related to our approach. Starting from
Shannon’s entropy as defined in information theory
(Shannon, 1948), their aim is to measure the uncer-
tainty or variability of workflow process models or
the information gained by the process design. For
example, it is concluded that the entropy of work-
flows consisting of purely serialized tasks or AND-
splits have zero entropy as there is no uncertainty re-
garding which tasks are going be executed in process
instantiations. On the other hand, the inclusion of
XOR-plits, OR-splits and loops in a process increase
entropy as one is not aware upfront which tasks are
going to be executed (or even their frequency). Each
of these uncertainties can then be derived, given an
assumed probability of each branch or loop iteration.
However, this approach differs from the approach we
will take in Section 4 and onwards. First, Jung (2008)
employs the entropy definition from information the-
ory, whereas our approach will focus on the statis-
tical thermodynamics perspective. Next, their mea-
sures are aimed at studying the design-time structure
of business processes, whereas we will use entropy to
focus on the run- or execution-time analysis of busi-
ness processes.
3 NORMALIZED SYSTEMS
Normalized Systems theory (NS) is about the de-
terministic creation of evolvable modular structures
based on a limited set of provenand unambiguous de-
sign theorems, primarily aimed at the design of evolv-
able software architectures. First, we will discuss the
essence of NS in its initial form, i.e., starting from
the stability point of view from systems theory. Next,
the recent association and indications towards confor-
mance with entropy concepts from thermodynamics
will be highlighted.
3.1 NS and Stability
Normalized Systems theory initially started from the
well-known maintenance problems in software appli-
cations, as was for instance already articulated ear-
lier by Manny Lehman in his “Law of Increasing
Complexity”. This law states that software programs
become ever more complex and badly structured as
they are changed and evolve over time and hence
become more and more difficult to adapt (Lehman,
1980). Based on the systems theoretic stability, this
phenomenon was related to the concept of combina-
torial effects: a change in modular structure of which
the impact or effort to implement it, is related to the
size of the system (on which the change is applied to)
(Mannaert et al., 2011, 2012). Indeed, given the as-
sumption that software applications keep on growing,
this means that the same type of change requires more
effort as time goes by. In contrast, systems which are
free of such combinatorial effects (for a defined set of
anticipated changes) are called Normalized Systems.
These systems comply with stability as defined in sys-
tems theory as a bounded impact always results in a
bounded output function (effort), even if time t → ∞.
For this stability to be reached, the following de-
sign theorems were proposed and formally proven to
be necessary conditions regarding the avoidance of
combinatorial effects (Mannaert et al., 2011, 2012):
• Separation of Concerns: each concern (in terms
of change drivers) should be separated in its own
distinct action entity;
• Separation of States: the calling of action entities
by other action entities should be performed in a
stateful way;
• Action Version Transparency: the updating of ac-
tion entities should not not have any impact on its
calling action entities;
• Data Version Transparency: the updating of data
entities should not have any impact on the action
entities receiving the data entity as input or pro-
ducing it as output.
As the construction of such stable software—
strictly adhering to the above described principles—
is not straightforward and current software constructs
Second International Symposium on Business Modeling and Software Design
130

do not offer by themselves any mechanisms for soft-
ware developers to obey them, a set of five elements
was proposed: data elements, action elements, work-
flow elements, connector elements and trigger ele-
ments. As these elements offer recurring structures
of constructs to facilitate the application of the previ-
ous principles, NS applications are traditionally build
as an aggregation of instances of these elements.
3.2 NS and Entropy
Recently, efforts were made to explain the above-
mentioned in terms of entropy as defined in thermo-
dynamics (Mannaert et al., 2012). First, the Boltzman
definition in statistical thermodynamics was adopted
considering entropy as the number of microstates con-
sistent with a certain macrostate. As such, microstates
were defined as binary values representing the correct
or erroneous execution of a construct of a program-
ming language. The macrostate is then to be seen
in terms of loggings or database entries representing
the correct or erroneous processing of the considered
software system. In order to control the defined en-
tropy, the earlier proposed theorems seem to be use-
ful as well. Regarding the Separation of States prin-
ciple, for instance, synchronous stateless pipeliness
typically do not keep state when calling other action
entities. As such, in case an error occurs, it not clear
which particular action entity ‘caused’ the failure. In
terms of the Separation of Concerns principle, each
concern should again be isolated in its specific con-
struct to avoid the creation of multiple microstates
for one macrostates. This time however, concerns
should be identified based on so-called uncertainty
drivers instead of change drivers. The other two re-
maining principles, Data Version Transparency and
Action Version Transparency, seem less applicable as
they are related to compile-time and not for run-time
analysis. However, two new theorems were suggested
from this viewpoint:
• Data Instance Traceability, requiring each ver-
sion and values of an instance of a data structure
to be tracked;
• Action Instance Traceability, requiring each ver-
sion and thread of an instance of a processing
structure to be tracked.
Indeed, not exporting this information to an observ-
able macrostate would lead to multiple possible mi-
crostates consistent with the same macrostate.
4 USING ENTROPY FOR
BUSINESS PROCESS ANALYSIS
In order to extend the concept of entropy to busi-
ness process analysis, we will first propose a defini-
tion of entropy, microstates and macrostates in a busi-
ness process context. Next, we will illustrate the ex-
istence of such entropy by means of an example and
discuss how NS principles can be helpful in reducing
the amount of entropy in business process systems.
4.1 Defining Entropy Concepts in
Business Process Systems
Our purpose is to apply the concept of entropy as de-
fined in statistical thermodynamics (i.e., the number
of microstates consistent with the same macrostate)
to business processes. Consequently, a first effort
should be directed towards interpreting macro- and
microstates in such context. While the stability view-
point (cf. Section 3) analyzes modular structures at
design time, an entropy based analysis tends to in-
vestigate the modular structures during or after their
execution (i.e., run time). Hence, regarding the
macrostate (i.e., the whole of macroscopic properties
of a system), typical externally observable properties
of a business process might include:
• throughput or cycle time (how long did the pro-
cess take to be executed?);
• quality and other output related measures (e.g.,
succesful or non-succesful completion of the pro-
cess as a whole or the number of defects detected
after the execution of the process);
• costs involved in the process;
• other resources consumed by the process (such
as raw materials, electricity, human resources,
etcetera).
Typical microstates (i.e., the whole of microscopic
properties of a constituent modules or particles of
the system) related to the above sketched macrostate
might then comprise the throughput time of a single
task in the process, the correct or erroneous outcome
of a single task, the costs related to one activity or
the resources consumed by one particular task of the
considered business process. Analyzing instantiated
business processes in terms of these defined macro-
and microstates would then come down to manage-
ment questions such as:
• which task or tasks in the business process was
(were) reponsible for the extremely slow (fast)
completion of this particular instance of the busi-
ness process? ;
On the Applicability of the Notion of Entropy for Business Process Analysis
131

• which task or tasks in the business process was
(were) responsible for the failure of the consid-
ered instantiated business process? ;
• which activities contributed substantially or only
marginally to the overall cost or resource con-
sumption of the considered business process (cf.
cost-accounting and management approaches like
Activity Based Costing)?
In case the answer to these questions is unam-
biguous and clear, the entropy in the system (here:
business process) is low (or ideally zero) as a par-
ticular macrostate (e.g., the extremely long through-
put time) can be related to only one or a few mi-
crostates (e.g., activity X took three times the normal
duration to be carried out, whereas all other activi-
ties finished in their regular time span). On the other
hand, when no direct answer to these questions can be
found, entropy increases: multiple microstates (e.g.,
prolonged execution of activities X and/or Y and/or
Z) could have resulted in the observed and possibly
problematic macrostate (e.g., the lengthy execution of
the overall process). This phenomenon seems to cor-
relate well with the three basic entropy interpretations
we listed in Section 2.1. First, business process anal-
ysis is more complex as the analyst has to consider
the whole system at once, not being able to refine his
problem analysis to certain clearly isolated parts of
the system. Second, uncertainty is present when try-
ing to perform remedial measures or optimizations.
Indeed, it is simply not known where possible prob-
lems are situated, and the outcome or success of spe-
cific adaptations in the business process repository is
uncertain as well. Finally, the tendency of particles to
dissipate is reflected in the fact that the “traces” of one
problematic activity are dispersed over the considered
system as a whole. In essence, unless a consciously
introduced separation is introduced, the information
and outcome of all three possible problem causing ac-
tivities (X, Y and Z) interacts before being exposed to
the observer (in this case the measurements are aggre-
gated). Hence, from an (enterprise) engineering view-
point, it would seem appealing to control and reduce
the entropy confronted with.
4.2 Illustrating Entropy in Business
Process Models
In order to illustrate our conceptualization of the man-
ifestation of entropy in business processes, consider
the following example as depicted in the BPMN no-
tation of Figures 1(a) and 1(b). Let us assume that
both processes represent a part of a typical assembly
line in which automobiles are finalized during their
manufacturing. More specifically, we will claim that
both process parts represent the manual attachment of
the weels (X) and doors to the car (Y), as well as the
spraying of a final liquid for the preservation of the
color of the car’s skeleton or “body” (Z). In Figure
1(a) all these activities are considered as one “final-
ization” activity P and only the throughput time for
this entity of work is registered. A possible frequency
graph of the throughput time of this way of model-
ing is represented in Figure 2(a) by means of a typ-
ical normal curve. Further, the sample mean T
p
is
given by the solid curve in this figure, while the “tar-
get mean”
2
set by the production manager is drawn
by a dashed line. In case statistical hypothesis testing
would point out that the observed mean actually sig-
nificantly differs from the target mean, the production
manager has no direct clue to determine which action
is accountable for the prolonged production through-
put time: both the attachment of wheels, doors or the
preservation spray as well as any combination among
them might be causing the delay. In entropy terms, the
macrostate in this situation is the throughput time of
process part P as a whole. The microstate is the com-
bination of the throughput times of each of the consti-
tuting activities X, Y and Z. Consequently, the mod-
eling as in Figure 1(a) exhibits a certain amount of
entropy as it is not clear which activity causes the pro-
longed overall throughput time. We can call this con-
fusion about the origin of a macrostate of a business
process in terms of its microstate a business process
uncertainty effect. Due to the inherent uncertainty and
doubt in this situation, an imperative and profound
study of the whole “finalization” activity should be
performed in order to retrieve the cause and solve the
problem identified.
On the other hand, Figure 1(b) makes the obvi-
ous break up of P into the constituting tasks X (place-
ment of the wheels), Y (placement of the doors) and
Z (preservation spray) and their throughput measure-
ments and means T
X
, T
Y
and T
Z
. The corresponding
normal curves of the frequency graphs are depicted
in Figure 2(b). In case of the same problem of an
enlarged overall average throughput time T
p
, the pro-
duction manager is now able to refine his analysis to-
wards the individual throughput times of X, Y and Z.
Again, the real observed sample means are depicted
in solid curves, the target means by the dashed line.
2
In realistic production environments, typical upper
control limits (UCL) and lower control limits (LCL) might
be employed to determine significant deviations from the
predefined goals. However, as this extra complexity does
not add any further insight to our conceptual example (nor
does it take the edge off our argument), we will leave this
feature out of scope in this paper as its extention is straight-
forward.
Second International Symposium on Business Modeling and Software Design
132
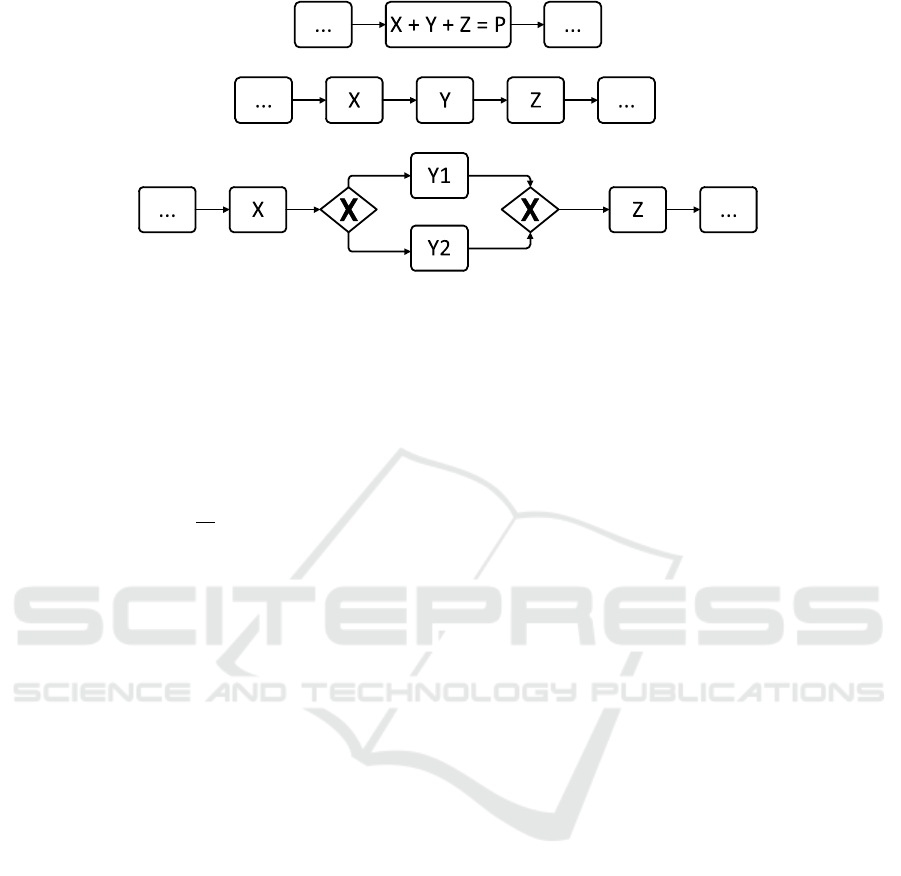
(a) Process variant A
(b) Process variant B
(c) Process variant C
Figure 1: Three business process variants in BPMN, illustrating different degrees of entropy.
For tasks X and Z, the dashed lines are not visible as
they coincide with the solide lines. Consequently, no
issues regarding a prolonged execution time of these
steps seem to be at hand. Regarding task Y however,
a larger standard deviation and significant difference
between the target mean and observed mean can be
found. In order to improve the observed overall av-
erage throughput time T
p
, improvements regarding
this specific business process task should be aimed
for. Hence, entropy (and uncertainty) can be said
to be reduced as the production manager can clearly
see that the extended throughput time (i.e., the same
macrostate as in our previous example) is caused by
only one particular task, the other activities having
regular throughput times (i.e., the macrostate is con-
sistent with only one microstate configuration).
4.3 Illustrating the Need for Principles
to Control Business Process Entropy
In the previous subsection, we illustrated how entropy
generation and uncertainty effects can occur in busi-
ness process models. Now we will illustrate how NS
principles facilitate the control and reduction of en-
tropy in the design of business processes.
Starting with the Separation of States principle,
this theorem would call for the stateful executions of
business processes. This would entail to include and
keep a unique state after the execution of each busi-
ness process activity. First, in terms of our previously
discussed examples as visually represented in Figures
1(a) and 1(b), this implies that after each step a state
should be pertained, registering the successful or un-
successful completion of the step as well as the rele-
vant observed system properties as costs, throughput
time, resource consumption, etcetera. Not including
these measure points or ‘mashing them up’ into one
activity as in Figure 1(a) would after all lead to the
uncertainty effect as described above. Second, these
states need to be uniquely defined after each activ-
ity for maintaining transactional integrity and keeping
record of exactly which activities have been executed.
For example, consider the case of a business proces
performing an application procedure for the entrance
of potential future university students. The process
contains multiple checks each resulting in a ‘positive’
state (after which the process can continue) or ‘neg-
ative’ state (in which the applicant is refused and the
process terminated). Here, a unique state should be
defined for each of the refusal situations in order to
keep record of the precise reason why one person has
been rejected. In case states are not uniquely defined
(e.g., each negative outcome receives the same state
‘refused’) one will not be able to trace the obtained
macrostate (i.e., a person has been refused) to the
correct microstate configuration (i.e., which reason—
which check—the person has been rejected for).
While the previous principle forces the usage of
states in order to isolate activities in the system of
which the macrostate is studied, the Separation of
Concerns principle discusses the nature of the ‘parti-
cles’ that have to be separated by the states or mea-
surement points. Stated otherwise, the division of
the system into its constituent parts (and hence mi-
crostates) should not be done in an arbitrary way.
Rather, concerns should be identified based on so-
called uncertainty drivers: each separate part of the
system of which the information should remain trace-
able for analysis purposes has to be isolated in its own
construct (e.g., task or process). This implies amongst
others that each task in a business process can con-
tain only one single non-redundant concern. Suppose
that in Figure 1(b) both tasks X and Y are combined
with an electronic circuit general test inspection activ-
ity Q (or another registration, measurement or quality
assessment activity) as both the wheel and door at-
On the Applicability of the Notion of Entropy for Business Process Analysis
133
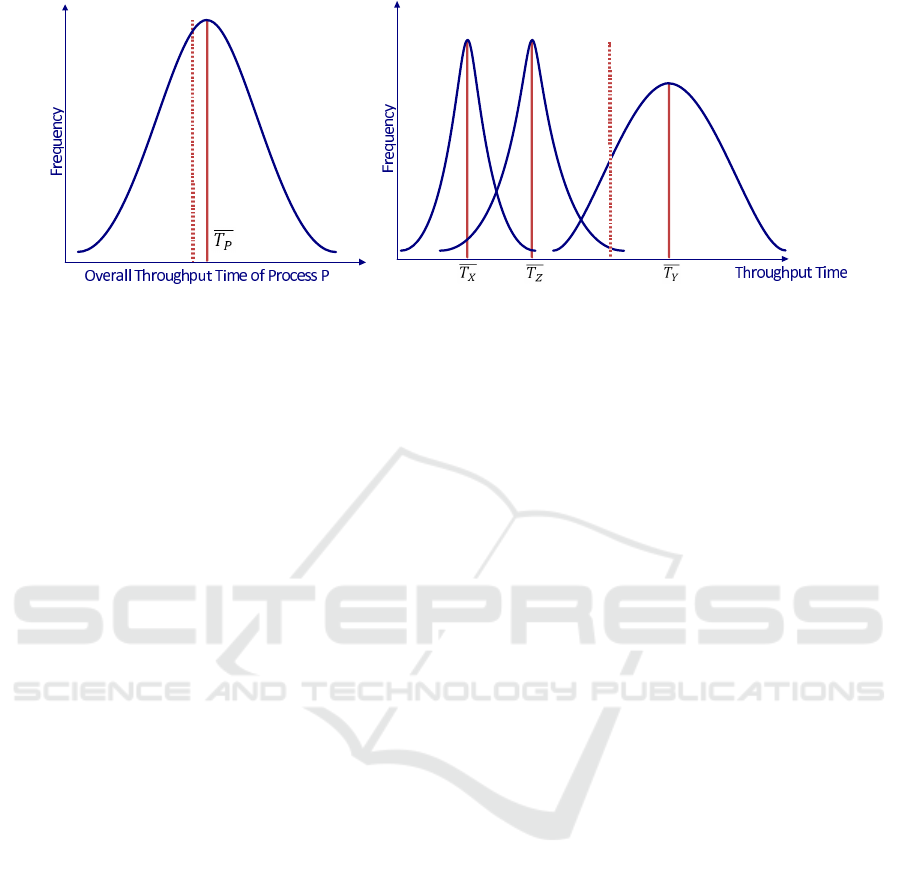
(a) (b)
Figure 2: Corresponding frequency graphs of the throughput time, based on the various ways of modeling.
tachment are supposed to have a possible influence
on the proper functioning of the electronic circuit of
the car. In case Q is not properly isolated in a dis-
tinct task and not resulting in its own unique states,
problem analysis of the overall troughput time point-
ing to X and/or Y is no longer unambiguous. First,
the block X + Q or Y + Q should be further scruti-
nized to determine whether X, Y or Q was causing
the throughput extension. Second, if investigation re-
veals a problem in the electronic circuit test Q, the
problematic observation is escalated into several in-
termediate states and remediating actions should be
taken at multiple process steps as well. As again
multiple microstates can be associated with the same
macrostate, entropy and uncertainty increase in such
situations. Moreover, recurring task sequences with
a clear business meaning of which information (e.g.,
its progress) is required to be recorded, should be iso-
lated in their separate construct (here: business pro-
cess) as well according to the same principle. Imag-
ine again the application procedure in which the ap-
plicants have to pay an administration fee in order to
be able to be assessed by the procedure and a regis-
tration fee later on if they have succesfully passed the
whole procedure and decide to enroll. In case this re-
dundant payment procedure (most likely repeated in
many other business processes as well) is not prop-
erly separated, a bottleneck in this fixed task sequence
might be much more difficult to be noticed. Consis-
tent problems in the payment procedure would show
up in many states (among many different processes)
but hide its relation to the payment concern. Again,
problems in such application procedure (macrostate)
might be related to many interwoven subsequences
(and hence microstates), resulting in a higher degree
of entropy.
The principle of Action Instance Traceability
would force us to keep track of the specific version
of a task which is executed and relate every state (and
measurement) to this specific task version. Also in a
business process context, it is not unlikely to imagine
situations in which a certain version of a task replaces
a predecing task or multiple versions (variants) of one
task exist concurrently. Consider for instance the situ-
ation in which our assembly line assembles both cars
with two (Y
1
) and four (Y
2
) doors respectively. Elabo-
rating on our investigation of througput time, it might
seem reasonable to assume that (given the same tech-
nical equipment and resource availability) the attach-
ment of doors for a two-door or four-door car variant
might differ significantly. Consequently, the specific
version should be recognized and traced individually
as depicted in Figure 1(c) in order to allow further
business process analysis and unambiguously relate
particular macrostates to the correct microstate con-
figuration (i.e., the specific versions) and avoid en-
tropy generation.
Finally, Data Instance Traceability in a business
process setting would prescribe us to keep track of
the specificities of the information object processed
by the business process in question. Applying the
concept to our car assembly example, this means that
characteristics of the car being assembled on a spe-
cific time slot should be tracked. Indeed, one can
imagine that specific difficulties reflected in the states
(e.g., extra costs, resource consumption, throughput
time) can arise depending on the type (model) of car
assembled on the same assembly line. Not tracking
these specificities results in multiple possible ‘causes’
(microstates) consistent with the same ‘problem’ or
’fact’ (macrostate). Hence, registration of the rele-
vant particularities of each processed information ob-
ject can be considered as another ‘rule’ to control en-
tropy.
Second International Symposium on Business Modeling and Software Design
134

5 REFLECTIONS
The concepts and principles discussed above might
have several consequences for the design and analy-
sis of business processes. We will first discuss some
theoretical implications, followed by a few practical
implications.
5.1 Theoretical Implications
Regarding the theoretical implications of employ-
ing an entropy viewpoint for analyzing business pro-
cesses, several issues can be noticed. First, as was al-
ready mentioned in our analysis at the software level
(Mannaert et al., 2012), the proposed analysis method
includes the assumption that the introduced states are
independent and decoupled. This means that they
should only reflect the outcome of the activities per-
formed in the module (here: task in a business pro-
cess) they are attached to. Stated otherwise, the re-
sulting state should not be dependent on the activi-
ties which have taken place earlier (e.g., in the busi-
ness process) and with which the studied activity is
coupled in a hidden (i.e., not explicitated) way. In
a business interpretation, this could for instance be
the case when the throughput time of task B is de-
pendent on decisions taken earlier in task A. For ex-
ample, it might be realistic to imagine a situation in
which the employees responsible for the execution of
task A choose to quickly (but poorly) finalize their
task (in order to minimize their own throughput time),
but having a pernicious consequence on the attain-
able throughput time of the execution of task B (for
which the employees might then be forced to invest
some extra time caused by the low-quality output of
their predecessors). This obviously only leads to lo-
cal optimizations, while preventing global optimiza-
tion. Entropy reduction by imposing such a “struc-
ture” is limited and even misleading as the states here
do not reflect the outcome of an isolated subsystem of
the regarded overall system. Indeed, from an analy-
sis viewpoint, it is no longer clear how the different
subsystems (hence, microstate configuration) brought
about the resulting macrostate. Hence, a clear inter-
face between both activities should be defined, includ-
ing (for example) unambiguous quality conditions as
output criteria for activity A and preconditions for the
execution of activity B. With the aim of preventing
such phenomena, this assumption adds to our earlier
call for the definition of completely and unambigu-
ously defined interfaces for (organizational) modules
in the first place (De Bruyn & Mannaert, 2012). Next,
efforts should be directed towards avoiding such cou-
pled modules.
Second, the initial application of the NS (en-
tropy related) principles at the business process level
demonstrated above, proved to be rather similar and
parallel to the software level, and not to contradict
with the guidelines by Van Nuffel based on the sta-
bility point of view (Van Nuffel, 2011). However, the
work of Van Nuffel primarily concentrated on identi-
fying business process instantiations of concerns to be
separated in terms of change drivers based on the sta-
bility rationale of NS . Hence, it would be interesting
to perform a similar study with the aim of identifying
typical business process instantiations of concerns in
terms of uncertainty drivers based on the entropy ra-
tionale of NS. This could lead to a parallel set of prac-
tical recommendations on how to design the modular
structure of business processes and their constituting
tasks. These guidelines would specifically allow for
maximum entropy control and facilitate unambiguous
analyses and tracking of outcomes obtained during
execution time.
Finally, in the NS rationale at software level, the
formulation of the principles (theorems) resulted in a
limited set of elements or patterns (recurring struc-
tures of constructs) which are instantiated and aggre-
gated consistently to build a software application. At
the organizational level, such patterns (fixed struc-
tures of business processes) would be appealing as
well when exhibiting both stability (i.e., proven ab-
sence of combinatorial effects towards a defined set
of anticipated changes) and controlled entropy (i.e.,
ex-ante known measurements or metrics to allow for
ex-post process analysis and optimization). The con-
struction of such organizational patterns would facili-
tate pattern instantiation which is both stable and isen-
tropic (i.e., having observablemacrostates of the over-
all system which can be unambiguously traced to a
microstate configuration). The formulation of such
patterns is obviously a very challenging effort, and
subject to future research. However, at the end of the
following subsection, we will give an illustration of
the usage of a recurring fixed pattern in reality for the
execution of certain business functionalities, leading
to entropy reduction.
5.2 Practical Implications
The reasoning in this paper holds irrespective of
the implementation method. Therefore, concrete in-
sights for supporting platforms for business processes
such as Service-Oriented Architectures (SOA) can be
made. In a SOA context, entropy is introduced in
a business process when information regarding the
micro-states of the service execution cannot be cap-
tured. However, the service concept specifically aims
On the Applicability of the Notion of Entropy for Business Process Analysis
135

to hide the implementation of its functionality behind
its interface. Consequently, micro-states which pro-
vide necessary knowledge during a service invocation
cannot be captured. Consider the following defini-
tion of a service from an often-cited author: “Ser-
vices are self-describing, platform-agnostic compu-
tational elements that support rapid, low-cost com-
position of distributed applications. Services per-
form functions, which can be anything from simple
requests to complicated business processes” (Papa-
zoglou, 2003, p. 3). This definition explicitly men-
tions the use of different distributed applications. In
the context of the throughput example, the usage of
such a service can result in delays caused by any ap-
plication (e.g., because of the program logic, its hard-
ware or its network connection). Consequently, the
distributed nature of a service by itself increases the
entropy when analyzing the business process.
Moreover, the design of services can introduce en-
tropy as well. The definition mentions the service
granularity. It seems that both fine-grained (i.e., “sim-
ple requests”) and coarse-grainedservices (i.e., “com-
plicated business processes”) are considered valid
by the definition. Nevertheless, our analysis indi-
cates that information concerning fine-grained modu-
lar building blocks is required to lower the business
process entropy. However, various authors discuss
how currently a trend towards more coarse-grained
services can be observed (e.g., Feuerlicht, 2006).
These so-called “enterprise services” attempt to mini-
mize the number of interactions needed to implement
a given business function in order to reduce the com-
plexity of the message interchange dialog (Feuerlicht,
2006). This example illustrates how considerations
from a technical point of view (e.g., lowering the
complexity of the message interchange dialog) may
conflict with considerations from a business point of
view (e.g., increasing the entropy during business pro-
cess analysis). Dealing with such conflicts is an im-
portant issue for a paradigm which positions itself as
the integration for business and IT perspectives. Nev-
ertheless, the service definition by itself does not seem
to provide guidance for entropy reduction. This task
remains the responsibility of the service designer.
While no silver bullet is currently available to de-
termine the “right” service granularity, certain inter-
esting domain-specific solutions are emerging. These
solutions apply the approach to controlling entropy as
presented in Section 2 (i.e., enforcing a certain recur-
ring structure) in order to ensure the availability of
required knowledge. Consider the example of manu-
facturing organizations who are operating in a global
supply chain. Governments of the national and inter-
national (e.g., the European Union) level define norms
and regulations on these supply chains. The monitor-
ing of these norms and regulations is executed by cus-
toms or quality inspections. In order to be able to per-
form these controls, certain information is required.
Because of the heteroginity of processes used in these
supply chains, any instance of these processes (e.g.,
a shipment) needed to be checked individually in or-
der to ensure compliance. Consequently, these con-
trols performed by the customs were very labor- and
time-intensive, and organizations considered them to
be a “necessary evil”. The common goal of govern-
ments and organizations should be to ensure compli-
ance to regulations, while having a minimal impact on
the planning and execution of supply chains. Based
on the introduction of structure in the organizational
processes, results have already been achieved towards
this goal. For example, member states of the Euro-
pean Union can grant the certificate of Authorized
Economic Operator (AEO)
3
to organizations which
follow, amongst others, customs compliance and ap-
propriate record-keeping criteria. AEOs can benefit
from simplified control procedures (e.g., fewer phys-
ical and document-based controls) during customs or
quality controls. An AEO commits himself to struc-
ture his processes according to certain landmarks,
which resemble the process states as discussed in the
Separation of States theorem in Section 4.3. Govern-
ments which publish such landmarks can ensure that
the information required for their controls can easily
be gathered based on the registration of these process
states. As a result, AOEs cannot use any SOA service
with a granularity which spans multiple landmarks.
Consequently, these landmarks effectively guide the
selection of service granularity by imposing an ap-
propriate structure on the processes, which is shown
to be required to control the entropy in them.
6 CONCLUSIONS
In this paper, we explored the usage of the entropy
concept for business process analysis. As such, the
paper has multiple contributions, while suggesting
several avenues for future research. First, we pro-
posed a specific way for analyzing business processes
from the typical engineering concept of entropy as
defined in statistical thermodynamics. This approach
seems to be contrasting with many ad-hoc or qualita-
tive best practice approaches suggested in extant liter-
ature. By means of some pedagogical and conceptual
examples, we showed that entropy has the tendency
to show up in business processes which are arbitrarily
3
See: http://ec.europa.eu/taxation customs/customs/
policy issues/customs security/aeo/
Second International Symposium on Business Modeling and Software Design
136

conceived, making it difficult to analyze them ex-post
(e.g., in terms of quality, costs, resource consump-
tion or throughput time). Consequently, in order to
optimize and control such business processes, we ar-
gue that they should be purposefully engineered with
the aim of controlling the entropy. Second, we pro-
posed some initial principles for entropy control in
business process systems (in analogy with previously
defined principles at the software level). Third, our
reflections demonstrated some of the implications of
this entropy based reasoning for both theoretical and
practical purposes, such as the design and usage of
Service-Oriented Architectures. Obviously, the pro-
posed principles might be further confined later on
and business process instantiations of concerns from
the entropy viewpoint (i.e., uncertainty drivers) could
constitute an interesting path for future research, as
would be the construction of organizational elements
or patterns incorporating these issues.
ACKNOWLEDGEMENTS
P.D.B. is supported by a Research Grant of the
Agency for Innovation by Science and Technology in
Flanders (IWT).
REFERENCES
Anderson, G. (2005). Thermodynamics of Natural Systems.
Cambridge University Press.
Boltzmann, L. (1995). Lectures on Gas Theory. Dover Pub-
lications.
De Bruyn, P. & Mannaert, H. (2012). Towards applying
normalized systems concepts to modularity and the sys-
tems engineering process. In Proceedings of the Seventh
International Conference on Systems (ICONS).
Feuerlicht, G. (2006). Service granularity considerations
based on data properties of interface parameters. Inter-
national Journal of Computer Systems science and Engi-
neering, 21(4), 315–327.
Hammer, M. (1990). Reengineering work: Don’t automate,
obliterate. Harvard Business Review, 68(4), 104 – 112.
Horowitz, I. (1970). Employment concentration in the com-
mon market: An entropy approach. Journal of the Royal
Statistical Society. Series A (General), 133(3), 463–479.
Huysmans, P. (2011). On the Feasibility of Normalized En-
terprises: Applying Normalized Systems Theory to the
High-Level Design of Enterprises. PhD thesis, Univer-
sity of Antwerp.
Jacquemin, A. P. & Berry, C. H. (1979). Entropy measure
of diversification and corporate growth. The Journal of
Industrial Economics, 27(4), 359–369.
Janow, R. (2004). Shannon entropy and productivity: Why
big organizations can seem stupid. Journal of the Wash-
ington Academy of Sciences, 90.
Jung, J.-Y. (2008). Measuring entropy in business process
models. In 3rd International Conference on Innovative
Computing Information and Control, 2008 (ICICIC ’08).
Jung, J.-Y., Chin, C.-H., & Cardoso, J. (2011). An entropy-
based uncertainty measure of process models. Informa-
tion Processing Letters, 111(3), 135 – 141.
Kettinger, W., Guha, S., & J.T.C., T. (1995). Business pro-
cess change: reengineering concepts, methods, and tech-
nologies, chapter The Process Reengineering Life Cycle
Methodology: A Case Study, (pp. 211–244). Idea Group
Inc (IGI).
Leff, H. (1996). Thermodynamic entropy: The spreading
and sharing of energy. American Journal of Physics,
64(10), 1261–1271.
Lehman, M. (1980). Programs, life cycles, and laws of soft-
ware evolution. Proceedings of the IEEE, 68(9), 1060 –
1076.
Mannaert, H., De Bruyn, P., & Verelst, J. (2012). Explor-
ing entropy in software systems: Towards a precise def-
inition and design rules. In Proceedings of the Seventh
International Conference on Systems (ICONS).
Mannaert, H., Verelst, J., & Ven, K. (2011). The transfor-
mation of requirements into software primitives: Study-
ing evolvability based on systems theoretic stability. Sci-
ence of Computer Programming, 76(12), 1210–1222.
Special Issue on Software Evolution, Adaptability and
Variability.
Mannaert, H., Verelst, J., & Ven, K. (2012). Towards evolv-
able software architectures based on systems theoretic
stability. Software: Practice and Experience, 42(1), 89–
116.
O’Neill, P. & Sohal, A. S. (1999). Business process reengi-
neering a review of recent literature. Technovation,
19(9), 571–581.
Palepu, K. (1985). Diversification strategy, profit perfor-
mance and the entropy measure. Strategic Management
Journal, 6(3), 239–255.
Papazoglou, M. P. (2003). Service-oriented computing:
Concepts, characteristics and directions. In Proceedings
of the Fourth International Conference on Web Infor-
mation Systems Engineering (WISE 2003), (pp. 3–12).,
Washington, DC, USA. IEEE Computer Society.
Shannon, C. (1948). A mathemathical theory of communi-
cation. Bell System Technical Journal, 28, 379–423.
Trienekens, J., Kusters, R., Kriek, D., & Siemons, P. (2009).
Entropy based software processes improvement. Soft-
ware Quality Journal, 17, 231–243. 10.1007/s11219-
008-9063-6.
Van Nuffel, D. (2011). Towards Designing Modular and
Evolvable Business Processes. PhD thesis, University of
Antwerp.
On the Applicability of the Notion of Entropy for Business Process Analysis
137
