Using Queueing Theory for Controlling the Number of Computing

Servers

Mark Sevalnev

, Samuli Aalto

, Jukka Kommeri

and Tapio Niemi

Aalto University, Helsinki, Finland

Helsinki Institute of Physics, CERN, Geneva, Switzerland

Keywords:

Energy Efﬁciency, Scientiﬁc Computing, Queueing Theory.

Abstract:

We have tested how queueing theory can be applied to improve energy efﬁciency of scientiﬁc computing

clusters. Our method calculates the number of required servers based on the arrival rate of computing jobs and

turns on and off computing nodes based on this estimate. Our tests indicated that this method decreases energy

consumption. However simultaneously the average lead time tends to increase because of higher waiting times

in cases when the arrival intensity goes up.

1 INTRODUCTION

It is natural to assume that the number of jobs sent to

a computing cluster varies throughout the day. The

problem of resource underutilization arises because

IT recourses are usually allocated according to the

peak load, which can last only for a short period of

time, forcing servers later become idle. Idle power

consumption can still be around 50% of the peak

power, causing a signiﬁcant energy loss.

We propose to save electricity by switching

servers on and off depending on the current need. In

the other words, we adjust the number of resources –

servers — to the amount of current workload – the ar-

riving intensity of jobs. Our solution is to use queue-

ing theory for deﬁning the problem and then applying

commonly known results to ﬁnd a suitable solution.

We tested our method in a dedicated test cluster

using job statistics collected from CERN (European

Organization for Nuclear Research) computing clus-

ter. Our test showed that the method can reduce elec-

tricity consumption over 10% without increasing the

average lead time more than 10%.

2 RELATED WORK

These days servers in data centers usually operate at

a very low utilization level, usually between 10 and

50 percent of the full power (Barroso and H

olzle,

2007). Because current server hardware is not energy-

proportional, an idle server still uses half of its peak

power leading to extremely inefﬁcient use of energy.

Thus it is desirable either to run servers near 100%

utilization or to keep them switched off.

Methods for improving energy efﬁciency of clus-

ter devices can be roughly divided into three cate-

gories: workload shaping, users’ behavior shaping,

and resource adjustment. Workload shaping is widely

used in network devices. Its idea is to use a proxy

between a service and a user that changes the incom-

ing trafﬁc through buffering to enable longer sleep

times for some continuous period of time and on the

other hand longer periods of high utilization (Nede-

vschi et al., 2008). Shaping users’ behavior is well

tried in electrical power companies, in which the price

of electricity is usually cheaper during low workload

activity periods e.g. nights. This encourages forcing

users to use electricity at least partly during the night

time leading to the smoother workload. A problem

with these methods is that they easily reduce quality

of service for users.

Resource adjustment means that computational

devices are switched off or put into sleep mode when

there is no workload. Solutions for resource ad-

justment have been studied most extensively. The

software solutions utilise power saving modes imple-

mented in hardware. The device enters and leaves

those modes depending on the current workload in-

tensity. The aim of software solutions is to es-

timate when it is appropriate to enter in a power

saving mode and when to leave it. An idea very

close to this approach is presented in (Meisner et al.,

Niemi T., Aalto S., Sevalnev M. and Kommeri J. (2012).

Using Queueing Theory for Controlling the Number of Computing Servers.

In Proceedings of the Sixth International Symposium on e-Health Services and Technologies and the Third International Conference on Green IT

Solutions, pages 83-88

DOI: 10.5220/0004474900830088

 SciTePress

2009), where switching off a server was associated

to use of power saving modes. Another option is

to use dynamic frequency and voltage scaling meth-

ods (DFVS). It decreases operating power of the

server but also degrades its performance (Kaxiras and

Martonosi, 2008). Related to this, many authors have

studied at which degree performance should be de-

creased to achieve electricity saving while preserving

the same, or almost the same, quality of service (Wu

et al., 2005)(Miyoshi et al., 2002)(Choi et al., 2004).

A crucial aspect of the solutions applying DFVS

and other power saving modes is to reveal the periods

of lower activity. Many different models have been

employed for this purpose. Queueing theory is quite

popular for such use as it nicely captures the relation-

ship between incoming trafﬁc, service efﬁciency and

quality of service. In (Gandhi et al., 2009) the au-

thors use queueing theory as the model which gives

the optimal number of running servers at each mo-

ment. A problem of queueing theory is that in order

to the predictions about queue length being valid it

is required that the incoming trafﬁc follows a Pois-

son process which is not usually true in wide area

networks (Crovella and Bestavros, 1995)(Paxson and

Floyd, 1995).

Control theory is another widely used model for

power management in computational clusters (Hor-

vath and Skadron, 2008)(Wang et al., 2008). In (Lin

et al., 2011) the authors represented the problem in

general optimization terms: they bound quality of ser-

vice and energy expenses together by expressing the

degraded service in terms of revenue lost due to users

abandoning the service. They also present an algo-

rithm that optimises the time series where the num-

ber of running nodes is an adjustable variable, the to-

tal cost is a target variable and the algorithm returns

the optimal number of running nodes for each period

of time. A similar approach, in which the problem

is modeled as an optimization problem with the aim

to minimize total cost, was used also in (Rao et al.,

2010)(Pakbaznia and Pedram, 2009)(Wendell et al.,

2010)(Liu et al., 2011).

Many approaches attack the problem of energy ef-

ﬁciency from a different angle; they try to improve

energy efﬁciency of the data center by taking into ac-

count the speciﬁc nature of cluster workload. In (Fan

et al., 2007) the authors found out that in thousands-

server-size data centers there is a 7% to 16% gap

between the achieved peak power and the theoreti-

cal peak power reported by the manufacturer. They

suggest to host additional servers under the existing

power budget and to mix different workloads to get

smoother combined workload. In (Govindan et al.,

2011) the authors propose to exploit data center unin-

terrupted power supplies (UPSs) during the increased

workload period to shave such power peaks. The

UPSs are then loaded during the lower activity work-

load. The authors present an algorithm which inves-

tigates the whole day workload and draw electricity

from UPSs during the highest activity.

Elnozahy et al.(Elnozahy et al., 2002) have stud-

ied cluster energy usage and evaluated different clus-

ter management policies and introduced a cluster

scale coordinated voltage scaling system. Their sim-

ulations show that dynamic cluster resource manage-

ment can save up to 42% of energy comsumption.

In their simulation the best performance is achieved

by combining coordinated voltage scaling with load

based server pool management.

3 MATHEMATICAL MODEL

We start to attack the problem by deﬁning the real

conﬁguration of the cluster. Thereafter we study

carefully the cluster characteristics which affect the

choice of a model. It turns out that there are only a

few crucial aspects that determine whether the use of

a model is justiﬁable. We discuss those aspects in de-

tail.

Description of the Cluster

We are dealing with a computational cluster, in which

there are server nodes connected in parallel via net-

work with each node consisting of multiple cores.

A population of users is sending jobs to the cluster.

An arriving job enters ﬁrst the batch scheduler queue,

from which it proceeds, in its turn, to a computational

node. By default a batch scheduler performs load bal-

ancing, i.e., it sends the next job to the node with the

least workload. The allowed number of jobs per node

is called slot number. Usually it equals the number of

cores per node, but it could be changed to an arbitrary

value. All jobs running on the same node are pro-

cessed simultaneously. If the number of jobs is less

than or equal to the number of cores, each job has its

own core. Otherwise a node performs process sharing

to share computational time equally between the jobs.

Queueing Model

The queueing model we propose for the cluster is nc

parallel and independent M/G/1-PS queues, where n

refers to the current number of active server nodes

(that are switched on), c to the number of cores per

node, and PS to the well-known processor sharing

queueing discipline. Each parallel M/G/1-PS queue

EHST/ICGREEN 2012

represents a single core. We assume that new jobs

arrive to the cluster according to a Poisson process

with intensity λ (arrivals per time unit), and an arriv-

ing job is sent to any of the parallel queues with equal

probabilities 1/(nc), independently of the states of

the queues and the other arrivals. Processing times of

jobs are assumed to be independently and identically

distributed (i.i.d.) with mean 1/µ. As a result, each

parallel queue behaves as an independent M/G/1-PS

queue with arrival rate λ/(nc). It is well-known (see,

e.g., (Kleinrock, 1976)) that the mean response time

E[T ] for such a system is given by

E[T ] =

µ −

. (1)

When the predeﬁned level of service is given by

means of the required mean response time E[T ], we

end up with the following dimensioning rule for the

required number n of parallel server nodes:

n =

λE[T ]

c(µE[T ] − 1)

(2)

Thus, in addition to ﬁx the level of service, E[T ],

we need to estimate the current arrival rate λ and the

mean processing time 1/µ to apply the formula.

Note that we do not model explicitly the batch

scheduler queue in front of the nodes. Including

such a queue in the model would result in a queueing

network representation with dependence between the

queues, viz., arriving jobs have to wait in the sched-

uler queue as long as all the slots are reserved in the

nodes. In addition, the state-dependent (i.e., closed-

loop) load balancing in the batch scheduler breaks

down the assumption that the arrivals in each paral-

lel queue constitutes a Poisson process. By omitting

the scheduler queue, we result in an approximative

but mathematically tractable model. In addition, the

load balancing property of the batch scheduler is re-

ﬂected in the model by splitting the arrival stream of

jobs evenly to all cores, which is an open-loop load

balancing method.

Another reason to justify the choice is that we as-

sume the number of running nodes to be sufﬁcient to

receive all currently arriving jobs. In this case, the

scheduler sends an arriving job immediately to a node

so that the scheduler queue remains empty most of the

time, thus diminishing its own role in the model. The

assumption is justiﬁed if the slot numbers are sufﬁ-

ciently large with respect to the total arrival rate λ.

Alternative Queueing Model

An alternative model, which also could be consid-

ered, is an M/G/k multi-server queue with k parallel

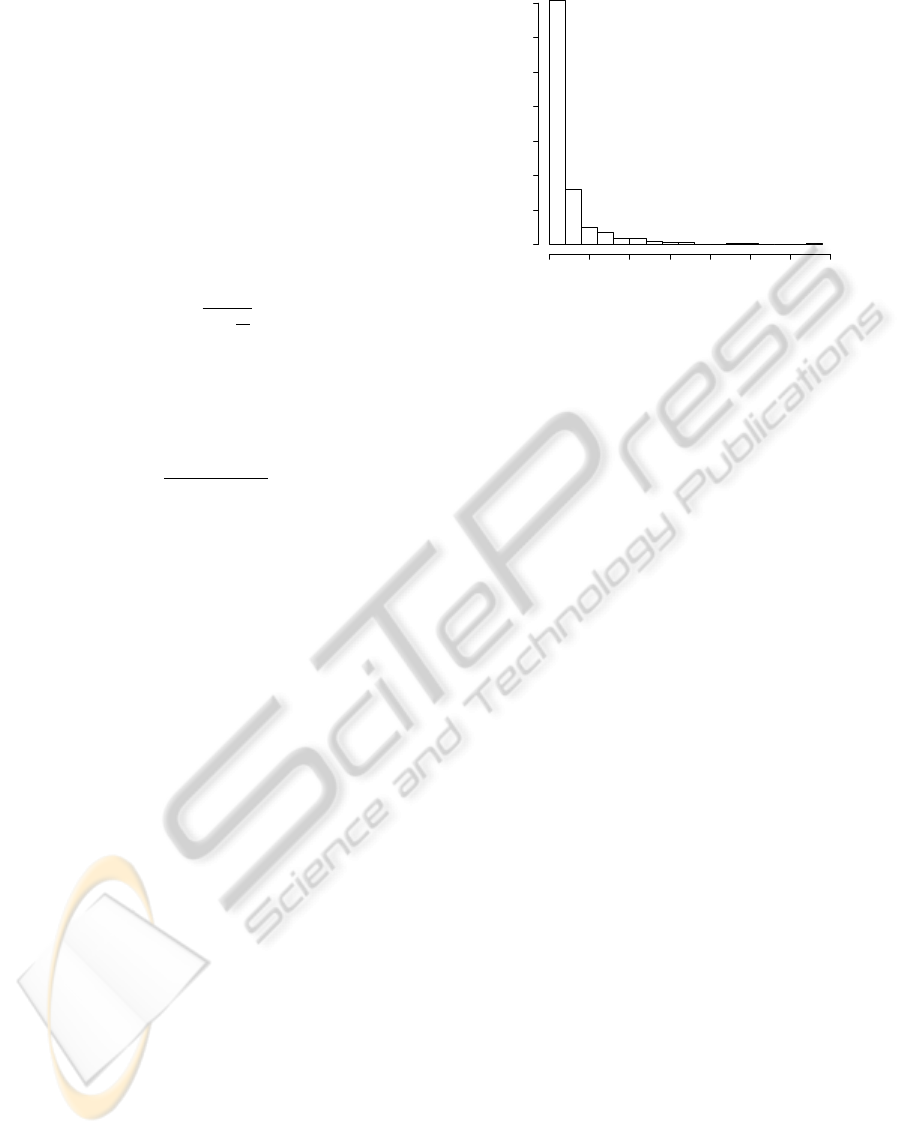
Interarrival time

Frequency

0 500 1000 1500 2000 2500 3000 3500

0 100 200 300 400 500 600 700

Figure 1: Interarrival times in a test data.

servers having a joint queue for all waiting jobs. In

this model, the parallel servers represent single cores

(and not the whole nodes) and the joint queue for

waiting jobs is an explicit model for the batch sched-

uler queue. The beneﬁts of this model are that (i) the

scheduler queue is preserved leading to a more natural

representation, and (ii) the closed-loop load balancing

is implicitly reﬂected by this multi-server queueing

model. The problem with this model is the fact that

speciﬁc cores belong to the same node and that it is

possible to send more jobs to the node than there are

cores on it. Thus, we leave the investigation of the

applicability of this model for future research.

Model Validation

Now we examine the interarrival times (Figure 1) be-

tween jobs from real cluster data and check whether

they follow exponential distribution as required by the

model.

We applied the well-known Kolmogorov-Smirnov

test to a real cluster data log for testing whether in-

terarrival times follow exponential distribution. We

picked up from the data log short intervals of vary-

ing length and performed Kolmogorov-Smirnov test

on them. We applied the test for 10 randomly chosen

time intervals – 3 of 20 samples, 3 of 30 samples, 3 of

40 samples and 1 of 50 samples. Their duration var-

ied from 3.32 minutes to 4.97 hours. It turned out that

6 of 10 passed the test. We argue that this is sufﬁcient

accuracy to apply queueing theory approach. In addi-

tion, the ﬁnal basis to use or not to use the approach

will be the amount of saved energy gained with the

aid of the method.

Analysis of the Empirical Processing

Time Distribution

While the key result (2) of our model is insensitive

Using Queueing Theory for Controlling the Number of Computing Servers

Process time (s)

Frequency

0 20000 40000 60000 80000

0 200 400 600 800

Figure 2: Distribution of process times.

to the form of the processing time distribution de-

pending just on its mean value, we still want to es-

timate the distribution itself. It is needed for our ex-

periments where we test the proposed energy-efﬁcient

algorithms for switching nodes on and off. The distri-

bution of processing times in our test data is shown in

Figure 2.

4 ALGORITHMS FOR

SWITCHING NODES ON AND

OFF

We implemented two algorithms that incorporate the

idea described above. The ﬁrst one, called Queue-

ing theory with averaging ﬁlter, operates as follows.

It takes m subsequent interarrival times of the last-

arrived jobs, and calculates the average from them.

To make the system better adapt recent changes in the

intensity, the time since the last arrival has also been

taken into account. The inverse of the average is used

as an estimate for the current arrival intensity. The es-

timate is substituted into the queueing theory formula

(2), which determines the number of nodes required

to process current workload with a given quality of

service and service efﬁciency. Based on this, we can

appropriately switch on additional nodes or switch off

unnecessary nodes.

The second algorithm, called Queueing theory

with exponential ﬁlter, follows the same approach as

the ﬁrst algorithm but it calculates the estimate for the

current arrival intensity by using exponential decay,

i.e., the last interarrival time is multiplied by a factor

C and the previous estimate (based on all previous in-

terarrival times) by 1 −C resulting in a new estimate,

which is the sum of these two terms.

The choice of m and C is a matter of ﬁne-tuning.

In our implementation, we chose m to be equal to 6

and C equal to 0.8, but of course in the further so-

lutions their effect should be investigated more care-

fully. The same applies to the choice of quality of

service, E[T ], the average response time in our case.

It has a predeﬁned ﬁxed value, which is twice the av-

erage processing time. In a more advanced algorithm,

the value should be also optimized, because in some

situations having slightly larger E[T ] may lead to con-

siderable energy savings.

The third algorithm is similar to the ﬁrst one ex-

cept a node is not disabled if the cluster queue has

any jobs left. In this way the number of resources is

decreased only if there are no jobs to process.

5 TESTS AND TEST

ENVIRONMENT

Our test cluster consists of one front-end server and

six computing nodes running a batch scheduling sys-

tem, Sun Grid Engine (SGE)(SGE, 2008). All the

servers in the cluster have two single core Intel Xeon

2.8 GHz processors (Supermicro X6DVL-EG2 moth-

erboard, 2048 KB L2 cache, 800 MHz front side bus)

with 4 gigabytes of memory and 160 gigabytes of disk

space. The operating system used was Rocks 5.4.3

with Linux kernel version 2.6.18. Servers are con-

nected with D-Link DGS-1224T 1GB switch.

The electricity consumption of the computing

nodes was measured with the Watts Up Pro electricity

consumption meter. We tested the accuracy of our test

environment by running the same tests several times

with exactly the same settings. The differences be-

tween the runs were around +-1% both in time and

electricity consumption.

We formed ﬁve test cases based on our algorithms

presented in Section 4:

1. Queueing theory with averaging ﬁlter,

2. Queueing theory with exponential ﬁlter,

3. Queueing theory with averaging ﬁlter and a con-

trol feature not to disable nodes if there are jobs

in the queue,

4. No control, i.e. all nodes running all the time, and

5. A simple control based on the cluster queue being

empty of not.

We calculated arrivals and processing times based

on data collected a scientiﬁc computing cluster at

CERN. The original data set contains all arrival

to three computing nodes during approximately 50

hours. The number of arrivals was 500. We scaled

EHST/ICGREEN 2012

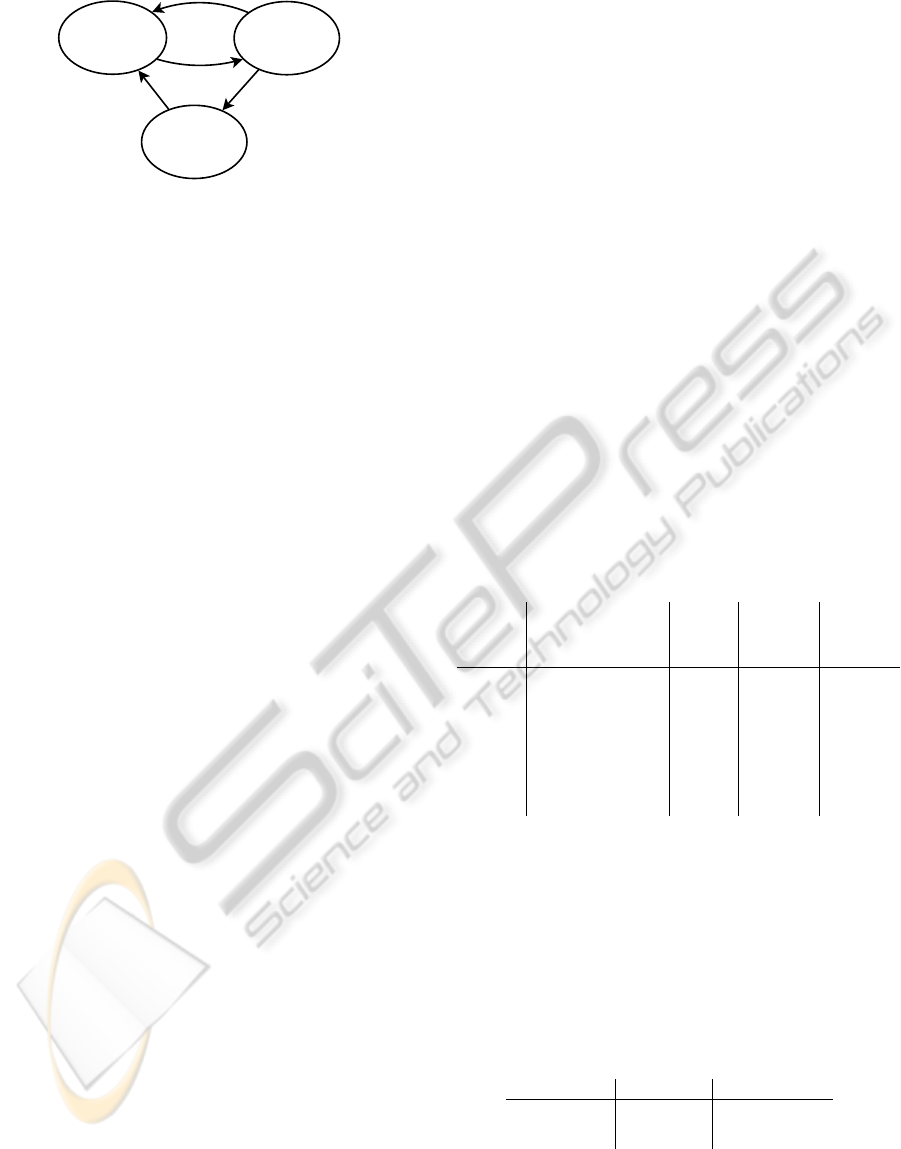
STOPPED

DISABLED

RUNNING

Figure 3: State diagram of a cluster computing node.

down the original interarrival times and processing

times to be able to run a test set in around ten hours.

As workload for all methods, we used the Beam-

beam application, which is a simulation tool been

used in the design of the LHC collider at CERN. It

simulates the beam-beam effect, i.e. the forces that

act on the beam when bunches of particles cross in the

LHC interaction points. These simulations are impor-

tant because beam-beam effect is one the major lim-

itations to LHC collider performance (beam, 2006;

Herr and Zorzano, 2001). The run time of the test ap-

plication was controlled artiﬁcially by terminating it

before ﬁnishing. This made it possible to have differ-

ent application run times, that would match the pro-

cessing times of the CERN cluster log data. Jobs were

sent and managed with the Sun Grid Engine.

The nodes of the cluster switch between three

states; 1) running, 2) disabled, 3) stopped. These

states are illustrated in Figure 3. In the running state

the computing node executes existing jobs and accept

new ones. In stopped state the computing node is

shutdown. Between running and stopped we have a

disabled state in which the computing node still pro-

cesses existing jobs, but does not accept new ones.

In Methods 1 and 2, a node was disabled if, ac-

cording to the queueing theory formula, there was too

many nodes running. A disabled node did not take

new jobs but continued computing existing jobs. Af-

ter all jobs were ﬁnished, the node was turned off.

Instead, in Method 3 if the estimated number of

running nodes does not increase and a disabled node

ﬁnishes its jobs, it will be turned off. If the inten-

sity increases and more nodes would be needed, a dis-

abled node will be switched back to the running state.

If there are no disabled nodes and the intensity in-

creases, a stopped node must be turned on. This is of

course a more expensive operation than just changing

a disabled node to the running state.

To test whether using queueing theory improves

results, we performed two control runs: 1) all nodes

running all the time, 2) switching nodes on and off us-

ing a simple control algorithm. The algorithm works

as follows: 1) A node is switched off if it has no jobs

and there are no jobs in the cluster queue. 2) A node

is switched on if there are jobs in the cluster queue.

The situation was checked every 40 seconds to avoid

too rapid changes.

6 RESULTS

Our test results showed that using queuing theory

models can reduce energy consumption by 9% to 17%

compared to no control at all. The most energy efﬁ-

cient method was still our simple method based on

jobs in the cluster queue (Method 5). It reduced en-

ergy consumption by 33%. In all methods the lower

energy consumption did not happen without a cost:

waiting time of jobs increased 135% to 264%. How-

ever, waiting times were relatively short compared to

the processing time that was the same 337 seconds in

all methods. The average lead time (waiting + pro-

cessing time) increased only 13% to 26%. Method 3

gave the best results when using both criteria: it re-

duced energy consumption 13.1% and increased the

average lead time 13.7%. The results are collected in

Table 1.

Table 1: Summary of test results.

Method Description Energy

(Wh)

Mean

waiting

time (s)

Mean

lead

time (s)

1 Averaging ﬁlter 9540 138 475

2 Exponential ﬁl-

ter

10380 89 426

3 Averaging ﬁlter

+ queue control

9939 89 426

4 No control 11443 38 375

5 Simple control 7660 124 461

To evaluate the system better, we also measured

idle consumption and server shutdown and powering

up energy costs in our test cluster. The results are

shown in Table 2. A server consumes 154W when

being idle and 3.54 W when switched off. From this

we can calculate that a server should switch off if it

were to stay idle for more than 160 seconds.

Table 2: Energy consumption of powering on and off a com-

puting node.

Time (s) Energy (Wh)

Power on 113.3 5.57

Power off 27.0 1.17

Using Queueing Theory for Controlling the Number of Computing Servers

7 CONCLUSIONS AND FUTURE

WORK

We developed a queuing theory model for controlling

a number of running computing nodes in a computing

cluster. The method observes arrival rate of incom-

ing computing jobs and estimates how many servers

should be running. The extra servers are then turned

off to save energy.

Energy savings and a possibly decreased service

level, i.e. increased waiting time in the cluster queue,

highly depends on changes in the arrival rate and pro-

cessing times of jobs. Therefore our future work will

focus on ﬁnding out how the parameters in the al-

gorithm should be set for different workloads. We

will also study alternative queueing theory models

and their suitability for the problem.

REFERENCES

Barroso, L. A. and H

olzle, U. (2007). The case for energy-

proportional computing. Computer, 40:33–37.

beam (2006). Lhc beam-beam studies. http://lhc-beam-

beam.web.cern.ch/lhc-beam-beam.

Choi, K., Soma, R., and Pedram, M. (2004). Dynamic Volt-

age and Frequency Scaling based on Workload De-

composition. In Int. Symp on Low Power Electronics

and Design.

Crovella, M. and Bestavros, A. (1995). Explaining world

wide web trafﬁc self-similarity.

Elnozahy, E. M., Kistler, M., and Rajamony, R. (2002).

Energy-efﬁcient server clusters. In In Proceedings of

the 2nd Workshop on Power-Aware Computing Sys-

tems, pages 179–196.

Fan, X., Weber, W.-D., and Barroso, L. A. (2007).

Power provisioning for a warehouse-sized computer.

SIGARCH Comput. Archit. News, 35:13–23.

Gandhi, A., Harchol-Balter, M., Das, R., and Lefurgy, C.

(2009). Optimal power allocation in server farms.

pages 157–168. ACM.

Govindan, S., Sivasubramaniam, A., and Urgaonkar, B.

(2011). Beneﬁts and limitations of tapping into stored

energy for datacenters. In ISCA, pages 341–352.

Herr, W. and Zorzano, M. P. (2001). Coherent dipole modes

for multiple interaction regions. Technical report,

LHC Project Report 461.

Horvath, T. and Skadron, K. (2008). Multi-mode energy

management for multi-tier server clusters. In Proceed-

ings of the 17th international conference on Parallel

architectures and compilation techniques, PACT ’08,

pages 270–279, New York, NY, USA. ACM.

Kaxiras, S. and Martonosi, M. (2008). Computer Archi-

tecture Techniques for Power-Efﬁciency. Morgan and

Claypool Publishers, 1st edition.

Kleinrock, L. (1976). Queueing Systems, volume II: Com-

puter Applications. Wiley Interscience. (Published in

Russian, 1979. Published in Japanese, 1979.).

Lin, M., Wierman, A., Andrew, L. L. H., and Thereska, E.

(2011). Dynamic right-sizing for power-proportional

data centers. In INFOCOM, pages 1098–1106. IEEE.

Liu, Z., Lin, M., Wierman, A., Low, S. H., and Andrew, L.

L. H. (2011). Greening geographical load balancing.

In SIGMETRICS, pages 233–244.

Meisner, D., Gold, B. T., and Wenisch, T. F. (2009). Pow-

ernap: eliminating server idle power. SIGPLAN Not.,

44:205–216.

Miyoshi, A., Lefurgy, C., Hensbergen, E. V., Rajamony, R.,

and Rajkumar, R. (2002). Critical power slope: Un-

derstanding the runtime effects of frequency scaling.

In In Proceedings of the 16th Annual ACM Interna-

tional Conference on Supercomputing, pages 35–44.

Nedevschi, S., Popa, L., Iannaccone, G., Ratnasamy, S.,

and Wetherall, D. (2008). Reducing network energy

consumption via sleeping and rate-adaptation. In Pro-

ceedings of the 5th USENIX Symposium on Networked

Systems Design and Implementation, NSDI’08, pages

323–336, Berkeley, CA, USA. USENIX Association.

Pakbaznia, E. and Pedram, M. (2009). Minimizing data

center cooling and server power costs. In Proceed-

ings of the 14th ACM/IEEE international symposium

on Low power electronics and design, ISLPED ’09,

pages 145–150, New York, NY, USA. ACM.

Paxson, V. and Floyd, S. (1995). Wide-area trafﬁc: The

failure of poisson modeling. IEEE/ACM Transactions

on Networking, pages 226–244.

Rao, L., Liu, X., Xie, L., and Liu, W. (2010). Minimizing

electricity cost: Optimization of distributed internet

data centers in a multi-electricity-market environment.

In INFOCOM, pages 1145–1153.

SGE (2008). BEGINNER’S GUIDE TO SUNTM GRID EN-

GINE 6.2 Installation and Conﬁguration. Sun Mi-

crosystems.

Wang, Z., Zhu, X., McCarthy, C., Ranganathan, P., and

Talwar, V. (2008). Feedback control algorithms for

power management of servers. In Third International

Workshop on Feedback Control Implementation and

Design in Computing Systems and Networks (FeBid),

Annapolis.

Wendell, P., Jiang, J. W., Freedman, M. J., and Rexford,

J. (2010). Donar: decentralized server selection for

cloud services. In SIGCOMM, pages 231–242.

Wu, Q., Juang, P., Martonosi, M., Peh, L.-S., and Clark,

D. W. (2005). Formal control techniques for power-

performance management. IEEE Micro, 25(5):52–62.

EHST/ICGREEN 2012