TARGET DETECTION USING FORWARD SCATTERING
RADAR WITH GPS RECEIVERS
Christo Kabakchiev
Faculty of Mathematics & Informatics, Sofia University, 125 Tzarigradsko shose Blvd., Sofia, Bulgaria
Vera Behar
Institute of Information & Communication Technologies, BAS, 25-A Acad. G.Bonchev Str., Sofia, Bulgaria
Herman Rohling
Department of Telecommunications,TU hamburg-Harburg, Hamburg,Germany
Keywords: Forward scattering radar, target detection, GPS signal processing
Abstract: A possible algorithm for target detection in a GPS-based Forward Scattering Radar is considered. The FSR
system consists of a transmitter mounted on a satellite of GPS and a receiver located on the Earth’s surface.
Theoretical calculations are presented using the secondary application of the GPS L5 signal. The numerical
results illustrate the idea of target detection in GPS-based FSR.
1 INTRODUCTION
Forward Scattering Radar (FSR) is a specific type of
bistatic radars that operate in the narrow area of the
forward scattering effect where the bistatic angle is
close to 180
0
, and the target moves near the
transmitter-receiver baseline. In FSR the Babinet’s
principle is exploited to form the forward scatter
signature of a target (Chernyak, 1999). According to
this principle, the drastic enhancement in scattering
is created due to the forward scattering effect. This
type of radar provides a countermeasure to ‘stealth’
technology because due to the forward scattering
effect, the Radar Cross Section (RCS) of targets
extremely increases (by 2-3 orders) and mainly
depends on the target’s physical cross section and is
independent of the target’s surface shape and the
absorbing coating on the surface. However, FSR has
some fundamental limitations, which are the absence
of range resolution and operation within very narrow
angles (±10
0
) (Cherniakov et al., 2006).
In this paper a passive FSR system where the
satellites of the GPS system are exploited as
‘illuminators of opportunity’ is considered. (Fig. 1).
The civil L1 signal is transmitted by satellites at
1572.42 MHz and contains the coarse acquisition
(C/A) code, which is unique for each satellite. The
C/A code modulated signal is a BPSK signal with a
chip rate of 1.023 MHz and the repetition interval of
1ms. The L1 signal frequency bandwidth is 2.046
MHz. The idea to apply a GPS L1 receiver to FSR
for air target detection is firstly discussed in (
Koch
and Westphal, 1995
). Some experimental results of a
GPS L1 receiver concerning detection of air targets
are shown and discussed in (
Suberviola et al., 2012).
However, modernization of GPS provides a good
opportunity to use the improved properties of a new
designed civil GPS signal L5 in FSR, which exploits
GPS as a non-cooperative transmitter. The major
innovations of the signal L5 signal, with respect to
GPS L1 signal, are the additional NH code
modulation and the use of a pilot channel free of
data (
Mongredien et al., 2006).
Figure 1. FSR topology
Transmitter Target Receiver
Earth
60
Kabakchiev H., Behar V. and Rohling H.
TARGET DETECTION USING FORWARD SCATTERING RADAR WITH GPS RECEIVERS.
DOI: 10.5220/0005413900600064
In Proceedings of the First International Conference on Telecommunications and Remote Sensing (ICTRS 2012), pages 60-64
ISBN: 978-989-8565-28-0
Copyright
c
 2012 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Pilot
signal
Q
5
(n)
CFAR
Detection
Non-coherent
Integration
Code &Carrier
Tracking
Acquisition
Binar
y
Detection
CFAR
Detection
The L5 signal is transmitted at 1176.45 MHz with a
received power of -154 dBw, which makes the L5
signal four times stronger than the L1 signal. Two
quadrature components of the L5 signal, referred as
I5 and Q5, are bi-phase modulated with a different
PRN of length 10230 chips. The PRN codes are
generated at a 10.23 MChips/s rate, resulting in 1 ms
period. Therefore, the bandwidth of the L5 signal is
increased to 20.46 MHz, which is ten times wider
than the bandwidth of the L1 signal. The I5 and Q5
components are then modulated by a 10-bit NH-
sequence and a 20-bit NH-sequence, respectively.
Each bit of the NH-sequences is 1ms, resulting in
10ms period of the I5 component and 20ms period
of the Q5 component, respectively.
A possible algorithm for air target detection in a
GPS L5-based FSR system is described in (Behar
and Kabakchiev, 2011), and the detection
probability characteristics are calculated in (Behar et
al., 2011) for the case when low-flying and poorly
maneuverable (for example, helicopters) air targets
are detected on the background of a white Gaussian
noise, or in the presence of: Urban Interference
Environment or a Stand-off-Jammer (SOJ).
Our main aim in this paper is to show
perspectives of GPS-L5-based FSR systems to
reliably detect ground or marine targets when GPS
satellites are located at small elevation angles. Our
task here is to present a possible algorithm for
marine target detection and target parameter
estimation in a GPS receiver used in FSR and also to
roughly estimate the potential maximum target
detection range in conditions of sea clutter. A set of
experimental records of signals from a small boat
provided by the team of Birmingham University is
used in order to estimate Signal-to-clutter-plus-noise
ratio (SNR) and calculate the probabilities
characteristics.
2 SIGNAL PROCESSING
The general block-scheme of a possible algorithm
for target detection and parameter estimation is
shown in Fig.2.
Figure 2. FSR signal processing
The Q5 component from the front end including
filtering and down conversion is then sampled by the
A/D converter. The signal from satellite k after the
A/D conversion can be described as
)()cos()()()()(
205
nNnnNHncnAnQ
IFQ
+
=
ω
(1)
where n is discrete in time, ω
IF
that is the
intermediate frequency to which the front end has
down converted the carrier frequency, N(n) is the
total noise, and c
Q
(n) is the PRN code. The main
goal of acquisition is the roughly estimation of the
Doppler frequency and the (c
Q
·NH
20
) code delay of
the visible satellite. The tracking loops ensure that
the prompt correlator is synchronized with the
incoming pseudorandom (c
Q
·NH
20
) code. They also
synchronize the receiver local oscillator in frequency
and phase with each satellite signal carrier within the
period of the Q5 component of the GPS L5 signal. In
this manner, the correlation magnitude remains in
the real part only (in-phase component). Two
variants of algorithms can be used for target
detection. The first of them firstly integrates signal
within a moving window and then uses a CFAR
detector to indicate the target signal detection
(CFAR detection with non-coherent integration).
According to the second algorithm, a CFAR detector
firstly indicates whether the target signal is present
in each sample of the correlator output. After that
the binary detector indicates the target signal
detection (CFAR detection with binary integration).
For a GPS L5 receiver, the frequency bandwidth
is 20.46 MHz, and the noise level N
r
in decibels is
nearly -131 dB. The signal-to-noise ratio at the RF
front-end output of the GPS receiver can be written
as (
Glennon et al., 2006):
)4/(/
2
rtgrtrrec
NRGPNPSNR πσ ==
(2)
According to [2,6,7], the forward scatter RCS σ of a
target depends only on the physical cross section of
the target (A
tg
) and can be calculated approximately
as:
2222
/)(4/4 λπλπσ hlA
tg
==
(3)
In (3), A
tg
is the target physical cross section, and the
parameters h and l are geometrical dimensions of a
target. In order to obtain the SNR expression at the
input of a CFAR detector in FSR, we replace the
parameter σ in (2) by its expression (3).
)/()(
222
rtgrt
NRhlGPSNR λ =
(4)
At the output of the Code& Tracking loops the
signal-to-noise ratio is given by:
)/()(
222
rtgSPrt
NRGhlGPSNR λ =
(5)
where G
SP
is the processing gain of the cross-
correlator.
Target Detection Using Forward Scattering Radar With GPS Receivers
61

3 DETECTION PROBABILITY
The signal to-noise ratio (4) could be improved by
non-coherent or binary integration over M samples.
In the extreme case, when, for example, the target
moving in the forward scattering zone at velocity V
and crosses the baseline at an angle of nearly 90
0
,
the maximum integration time corresponding to
target visibility within the main lobe of the target
scattering pattern is given by:
)/(2
2
VldT
Rtg
λ = (6)
where d
R
is the distance from the receiver to the
point of crossing and it can be assumed that d
R
=R
tg
.
The number of integrated samples M can be
determined from (5) as:
]/[
5Qtg
TTEM =
(7)
where T
Q5
=20msec and E[.] is the integer part of the
fraction in brackets.
3.1 CFAR Detection with Non-coherent
Integration
In a CFAR detector, after non-coherent integration
of M samples of the signal intensity at the envelope
detector output, the following test statistics is
formed for each sample n in the time domain:
∑
−+
−=
=
12/
2/
2
)()(
Mn
Mnk
M
ksnq
(8)
The intensity in n
th
time discrete indicates signal
detection if the test statistics (7) exceeds an adaptive
threshold H
n
. According to [7], the decision rule for
detection is:
()
⎩
⎨
⎧
≥
=Φ
otherwise
KHnqif
n
nM
M
,0
)()(,1
(9)
The parameter K in (9) is the length of the reference
window used to estimate the total noise level. When
the noise intensity is unknown, the detection
threshold H
n
(K) in (9) is formed adaptively for each
integrated sample q
n
(M) of the signal intensity at the
envelope detector output. In a cell-average CFAR
detector the threshold H
n
(K) is formed as:
)()( KwTKH
nn
⋅
=
α
(10)
where Tα is the scale factor, ω
n
(K) is the average
power of the total noise calculated over samples if
the reference window.
∑
=
=
K
k
n
n
ksKw
1
2
)()(
(11)
The probability of false alarm p
FA
maintained at the
output of a CFAR detector can be calculated using
the following expression (Behar et al., 2011):
nK
n
K
n
FA
T
T
K
nK
P
+
−
=
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−+
=
∑
)1(
1
1
1
0
α
α
(12)
In the worst case when the signal intensity from the
target independently fluctuates according to the χ
2
-
law, the probability of detection at the output of a
CFAR detector is evaluated as follows [7]:
For 1≤ M ≤2:
∑∑
=
+−−
−
−=
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
j
n
nK
n
jM
j
Lj
D
T
T
nK
j
M
P
0
1
1
1
1
)1(
)(
1
1
1
2
α
α
α
α
β
α
(13)
For M>2
(
)
()
∑∑
∑∑
=
+−−
−
=
=
+−−
−
=
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−−
+
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
=
m
n
nK
n
mM
m
m
i
j
jK
j
iM
M
i
D
T
T
n
nK
M
mM
T
T
j
jKiM
P
0
1
1
1
0
0
1
2
3
0
)1(
)(
1
3
2
)1(
1
1
2
α
α
β
α
β
α
α
α
α
α
(14)
The parameters α and β in (13) and (14) are
evaluated as follows:
)4/1/(1 SNRM
⋅
+
=
α
and
α
β
−= 1
(15)
The parameter SNR in (15) is the average signal-to-
noise ratio evaluated by (5). The scale factor Tα
used in (13) and (14) is determined as a root of the
equation (12) for a fixed value of the false alarm
probability P
FA
.
3.2 CFAR Detection with Binary
Integration
All decisions Φ(n) at the CFAR detector output
obtained within M consequential time samples are
summarized and compared with a fixed integer
threshold L. The binary decision rule for target
detection is:
()
⎪
⎩
⎪
⎨
⎧
≥Φ
=Φ
∑
=
otherwise
Lnif
L
M
n
M
,0
)(,1
1
(16)
The probability of false alarm at the binary detector
output is:
nM
FA
n
FA
M
Ln
FA
pp
n
M
P
−
=
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑
)1()(
(17)
The parameter p
FA
in (17) is the probability of false
alarm maintained at the CFAR detector output,
which is calculated by (13). The probability of target
First International Conference on Telecommunications and Remote Sensing
62

detection at the binary detector output is calculated
analogically:
nM
D
n
D
M
Ln
D
pp
n
M
P
−
=
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑
)1()(
(18)
The parameter p
D
in (18) is the detection probability
at the CFAR detector output calculated for M=1.
3.3 Probability of Target Detection
According to the block-scheme of signal processing
(Fig.2), the probability of target detection can be
expressed by the following expression:
Dacqt
PPP ⋅=
arg
(19)
The parameter P
acq
in (19) is the probability of GPS
signal acquisition. For the sake of simplicity we
assume that outside the geometrical shadow of the
target (dead zone) this parameter is close to1.
4 NUMERICAL RESULTS
Before we calculate the probability of target
detection using the expressions (12-19) need to
determine the SNR at the cross-correlator output in
one period of the Q5 component of the GPS L5
signal (T
Q5
=20msec) because the SNR values are
used for calculating the parameters α and β in (15).
The SNR at the cross-correlator output is calculated
for a small target (h=1m and l=1m) as a function of
the distance to the target R
tg
. The SNR values
obtained are plotted in Figure 3. The following
parameters of the GPS L5 signal are used in
calculations: carrier frequency – f
o
=1176MHz
(λ=0.2551m); frequency bandwidth –
ΔF=20.46MHz, the GPS L5 signal power near the
Earth’s surface – P
t
=-154dBW.
Figure 3. SNR at the correlator output within 20msec
As shown in Figure 3, the SNR is calculated for four
values of the antenna gain: G
r
= [0; 10; 15; 35] dB.
The number of integrated samples at the
correlator output and the corresponding them
integration time for the case when the target crosses
the forward scattering zone and moving within it
perpendicular to the baseline with velocity 7.5 m/s
are plotted in Figure 4 depending on the distance to
the target.
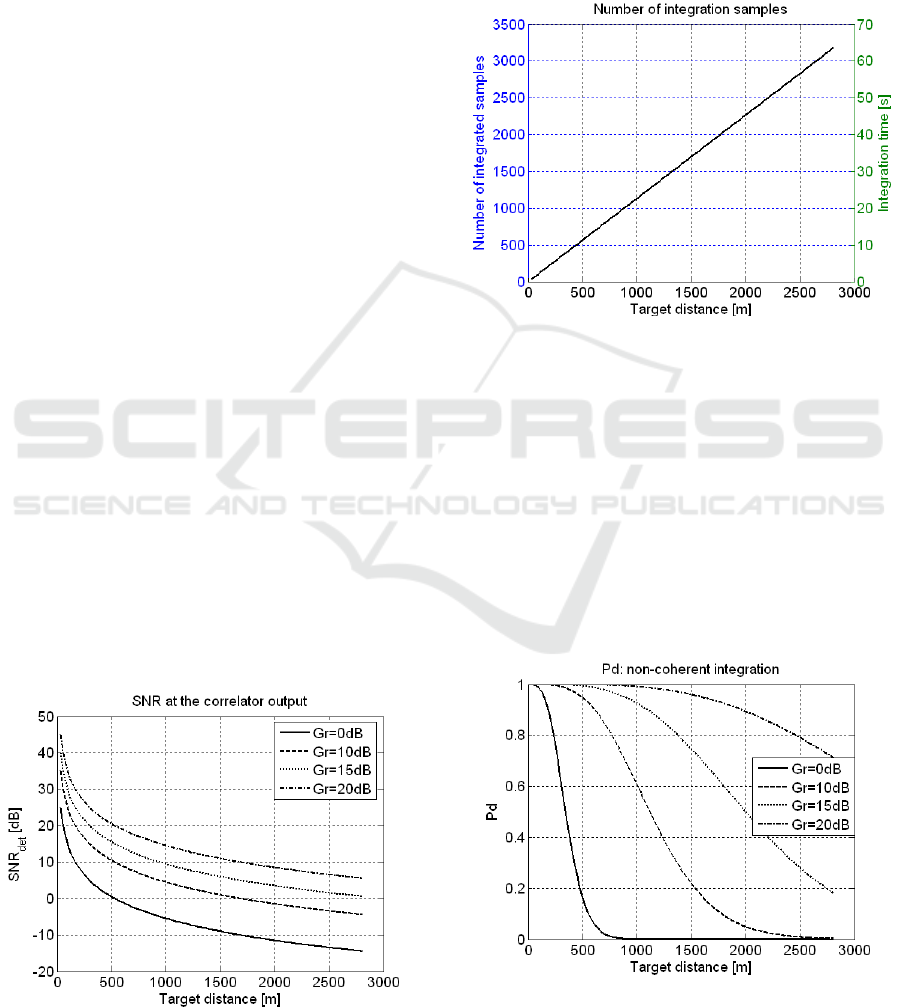
Figure 4. Number of integration samples (left) and the
corresponding integration time (right)
It can be seen that the integration time can be very
large and can reach to 60-70 sec for a target moving
with velocity 7.5 m/s (27km/hour).
The probability of small target detection with
non-coherent integration of the correlator outputs is
calculated as a function of the target distance and
shown in Figure 5. The probability of detection is
calculated by equations (12, 13, 14) for the false
alarm probability of 10
-7
. The SNR values at the
correlator output, which are used for calculation of
the probability characteristics by (12, 13, and 14),
are shown in Figure 3.
Figure 5. Probability of detection with non-coherent
integration for
P
FA
=10
-7
Target Detection Using Forward Scattering Radar With GPS Receivers
63

The number of integrated samples (M) used for
calculation of the probability characteristics is
shown in Figure 4 (left). The size of a reference
window (K) used in (13) and (14) is K= 60.
The probability of small target detection with
binary integration of the correlator outputs is
calculated as a function of the target distance and
shown in Figure 6. The probability of detection is
calculated by equations (17, 18) for the false alarm
probability of 10
-7
. After CFAR detection at the
correlator output the decision rule “L out of M” is
used for target detection. The values of the detection
probability plotted in Figure 6 are calculated for the
binary threshold L=2M/3, where M is the number of
integrated samples.
Comparing the two probabilities of detection, with
non-coherent and binary integration, it can be seen
that the detectability of targets strongly depends on
the antenna gain that the receiver creates in the
direction of the visible GPS satellite. Obviously, the
greater the gain of the antenna in the direction of
visible GPS satellites, so at large distances can be
detected a moving target in the forward scattering
area. For example, a small target that crosses the
forward scattering zone can be detected with
probability of 0.9 at the distance 2000m (with non-
coherent integration) or 1700m (with binary
integration) if the receiver antenna creates in the
direction of the visible GPS satellite the gain of at
least 20dB. The numerical results presented in
Figure 5 and 6 also illustrate that in case of the
omnidirectional antenna of the receiver (Gr=0dB),
small targets can be detected only at very close
distances (200m-300m) regardless of the type of
integration (non-coherent or binary).
Obviously, in conditions of interference, the
SNR in Figure 3 must be corrected taking into
account the ‘’interference-to-noise” ratio (INR).
Fig.6 Probability of detection with binary integration
L=2M/3 and P
FA
=10
-7
4 CONCLUSIONS
It is shown that forward scattering radar with a non-
cooperative GPS-based transmitter can be used for
detection of small targets on the background of a
white Gaussian noise if the receiver antenna creates
in the direction of the visible GPS satellite the
appropriate gain.
ACKNOWLEDGEMENTS
This work is financially supported by the Bulgarian
Science Fund (projects DTK 02/28.2009).
REFERENCES
Chernyak, V., 1999, Fundamentals of Multisite Radar
Systems
, Gordon and Breach Science Publishers.
Cherniakov, M., Abdullah, R., Jancˇovicˇ, P., , Salous, M.,
Chapursky, V., 2006, Automatic ground target
classification using forward scattering radar. In
IEE
Proc. on Radar Sonar Navig.,
vol. 153, no. 5, pp. 427
– 437, October 2006.
Koch,V., Westphal, R., 1995, New approach to a
multistatic passive radar sensor for air/space defense.
In
IEEE AES Systems Magazine, pp. 24-32,
November, 1995.
Suberviola, I., Mayordome, I., Mendizabal, J.,
Experimental results of air target detection with GPS
forward scattering radar, 2012, In
IEEE Geoscience
and Remote Sensing Letters
, vol. 9, no. 1, pp.47-51,
January 2012.
Mongredien, C., Lachapele, G., Gannon, M., Testing GPS
L5 acquisition and tracking algorithms using a
hardware simulator, 2006. In
Proc. of ION GNSS, Fart
Wart TX, , pp. 2901-2913, September 2006.
Behar V., Kabakchiev, Ch., Detectability of Air Target
Detection using Bistatic Radar Based on GPS L5
Signals, 2011. In
Proc. IRS’2011,12-th Intern. Radar
Symp
., Leipzig, pp. 212-217, September 2011.
Behar, V., Kabakchiev, Ch., Rohling, H., Air Target
Detection Using Navigation Receivers Based on GPS
L5 Signals, 2011. In
Proc. of ION GNSS’ 2011, 24th
International Technical Meeting of The Satellite
Division of the Institute of Navigation
, Portland OR,
pp. 333-337, September 2011.
Glennon, E., Dempster, A., Rizos, C., Feasibility of air
target detection using GPS as bistatic radar, 2006. In
Journal of Global Positioning Systems, vol. 5, no. 1-2,
pp. 119-126, 2006.
First International Conference on Telecommunications and Remote Sensing
64