GRAY-LEVEL IMAGE CONTOURS EXTRACTION
& COMPRESSION USING WAVELET TRANSFORM
Ali Abdrhman Ukasha
Faculty of Engineering, Sebha University, Brack, Libya
Keywords: Wavelet transform, Image compression, Contour extraction & compression, Ramer & Trapezoid methods.
Abstract: This paper presents a method of contour extraction and compression from grey level image. Single step
parallel contour extraction (SSPCE) method is used for the binary image after inverse wavelet transform is
applied to the details images. Then the contours are compressed using either Ramer or Trapezoid methods in
spatial domain. The proposed algorithms are applied in spectral domain using single-level wavelet
transform (WT). Effectiveness of the contour extraction and compression for different classes of images is
evaluated. In the paper the main idea of the proposed procedure for both contour extraction and image
compression are performed. To compare the results, the mean square error, signal-to-noise ratio criterions,
and compression ratio (bit per pixel) were used. The simplicity to obtain compressed image and extracted
contours with accepted level of the reconstruction is the main advantage of the proposed algorithms.
1 INTRODUCTION
Contour representation and compression are required
in many applications e.g. computer vision,
topographic or weather maps preparation, medical
images and moreover in image compression. The
transform coding method compresses image data by
representing the original signal with a small number
of transform coefficients. It exploits the fact that for
typical images a large amount of signal energy is
concentrated in a small number of coefficients. The
goal of transform coding is to minimize the number
of retained transform coefficients while keeping
distortion at an acceptable level. Transform coding
is an integral part of one of the most widely known
standards for lossy image compression, the JPEG
(Joint Photographic Experts Group) standard.
Contour extraction and image compression can be
obtained using transforms such as Fourier (Brigham,
1974), Walsh (Walsh, 1923), DCT (Clarke, 1985),
Wavelet (Vetterli, Martin, Kovacevic, 1995) and
Periodic Haar Piecewise-Linear (PHL) which is
based on the integration of Haar functions (Dziech,
Belgassem, Nern, 2000) and (Dziech, Belgassem,
Aboukhres, 1996 ). In this paper the discrete wavelet
transform will be used. The forward wavelet
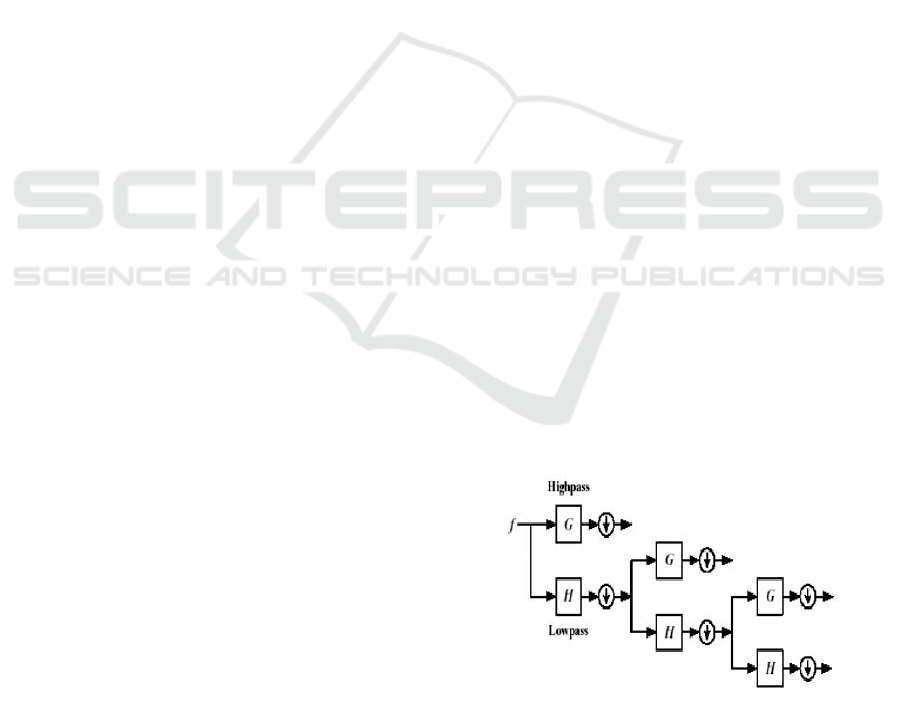
transform is applied to the grey-level image as
shown in Figure 1.
To obtain the compressed image and binary
image, inverse wavelet transform is applied to the
approximation coefficients image and details
coefficients images respectively. The contours are
extracted from binary image using single step
parallel contour extraction (SSPCE) method
(Dziech, Besbas, 1997) and (Besbas, 1998). Finally
the compressed contours are obtained using either
Ramer or Trapezoid methods.
Figure 1: Image analysis using discrete wavelet transform.
Flowchart of the algorithm for image
compression and contour extraction is depicted in
Figure 2.
99
Ukasha A.
GRAY-LEVEL IMAGE CONTOURS EXTRACTION COMPRESSION USING WAVELET TRANSFORM.
DOI: 10.5220/0005414600990104
In Proceedings of the First International Conference on Telecommunications and Remote Sensing (ICTRS 2012), pages 99-104
ISBN: 978-989-8565-28-0
Copyright
c
 2012 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 2: Block diagram of image compression and
contour extraction of grey level image using single level
of wavelet transform.
2 DISCRETE WAVELET
TRANSFORM (DWT)
The Wavelet analysis is an exciting new method for
solving difficult problems in mathematics, physics,
and engineering, with modern applications as
diverse as wave propagation, data compression,
signal processing, image processing, pattern
recognition, computer graphics, the detection of
aircraft and submarines and other medical image
technology (Vetterli, Martin, Kovacevic, 1995) and
(Gonzalez, 1987). Wavelets allow complex
information such as music, speech, images and
patterns to be decomposed into elementary forms at
different positions and scales and subsequently
reconstructed with high precision.
Wavelets are obtained from a single prototype
wavelet called mother wavelet by dilations and
shifting using the equation
)(
1
)(
,
a
bt
a
t
ba


(1)
3 RAMER ALGORITHM
Contour is represented as a polygon when it fits the
edge points with a sequence of line segments. There
are several algorithms available for determining the
number and location of the vertices and also to
compute the polygonal approximation of a contour.
The well known is Ramer method which is based on
the polygonal approximation scheme (Ramer, 1972).
The simplest approach for the polygonal
approximation is a recursive process (Splitting
methods). Splitting methods work by first drawing a
line from one point on the boundary to another.
Then, we compute the perpendicular distance from
each point along the segment to the line. If this
exceeds some threshold, we break the line at the
point of greatest error.
The idea of this first curve approximation is
illustrated in Figure 3.
4 0 42 44 46 48 50 52 5 4 5 6 5 8
8 8
9 0
9 2
9 4
9 6
9 8
10 0
10 2
10 4
D
C
B
A
m a x im u m dis tance
(d)
m a x imu m distance
(d)
y
x
Figure 3: Curve approximation by Ramer algorithm.
4 TRAPEZOID ALGORITHM
The idea of this algorithm consists in segmentation
of the contour points to get trapezoid shapes (points
of SP, B, C, and EP) (Ukasha, Dziech, Elsherif,
2009) and (Ukasha, 2010).
The first and last points of each segment are
called starting point (SP) and ending point (EP)
respectively. The fit criterion is the ratio between
distance between B and C points (dBC), and the
distance between C and EP points (dCEP), as
illustrated in Figure 4, and is defined by equation
(2).
th
dCEP
dBC

)/( (2)
Comparison
Forward
wavelet
transform
Grey
level
image
Compressed
image from
approximation
coefficients
Contour
extraction using
SSPCE
Binary Image
from details
coefficients
idwt
idwt
Contour
compression
using Ramer/
Trapezoid
methods
details
approxi
mation
First International Conference on Telecommunications and Remote Sensing
100

Figure 4: Illustration of the basic trapezoid idea for the
Trapezoid method.
5 APPLIED MEASURES
The proposed image compression and contour
extraction method is related to the data compression
and extraction problems. To evaluate its compress-
ion ability, the following compression ratio was
introduced if each pixel is implemented by eight
bits.
)*(
8*
mn
ZS
bpp 
(3)
where:
NOZ - number of zero coefficients
ZS - coefficients number in the desired zonal
n * m - size of the image
The mean square error (MSE) and peak signal-to-
noise ratio (PSNR) criterions were used to evaluate
the distortion introduced during the image
compression and contour extraction procedures. The
MSE criterion is defined by the following equation:

 

n
i
m
j
jiIjiI
mn
IIMSE
0 0
2
~~
)),((),((
)*(
1
),(
(4)
where
I
is the original image, and
~
I
is the
reconstructed image.
6 EXPERIMENTS RESULTS
To visualise the experimental results a set of five test
grey levels images were selected. Selected images
are shown in Figure 5.
(a) (b)
Figure 5: Test images: a) Tools (256x256), and b) Baby
(128x128).
The decomposition of Tools image using first
level of DWT is shown in Figure 6.
Figure 6: Tools image decomposition using first level of
DWT.
The compressed Tools image can be obtained
using approximation coefficients only as shown in
Figure 7 (related results are shown in the Table 1).
(a) (b)
Figure 7: Tools image reconstruction using
approximation coefficients: a) Original image, and
b) Compressed image.
C
B
EP
SP
dCEP
dBC
Gray-Level Image Contours Extraction & Compression Using Wavelet Transform
101

Table 1: Tools image results.
MSE PSNR [db] Bit Per
Pixel (bpp)
b) 24.61 34.22 2
The extracted contours using SSPCE method for
contour extraction of Tools image are obtained using
horizontal, vertical, and diagonal coefficients as
shown in Figure 8.
(a) (b)
Figure 8: Tools image: (a) Binary image from details
coefficients, and (b) Contours extraction using
SSPCE method.
The compressed contours for Tools image are
obtained using Ramer and Trapezoid methods are
shown in Figure 9 (related results are shown in the
Table 2).
Table 2: Tools image results.
Measures
Method
(Compression)
MSE PSNR
[db]
CR Elapsed
Time
a) Ramer 0.0175 17.58 69.46 10.65
b) Trapezoid 0.0174 17.59 69.34 10.40
c) Ramer 0.0199 17.02 78.99 8.82
d) Trapezoid 0.0197 17.05 78.57 8.31
e) Ramer 0.0226 16.47 89.80 7.35
f) Trapezoid 0.0225 16.47 89.62 7.27
where CR is the compression ratio.
(a) (b)
(c) (d)
(e) (f)
Figure 9: Tools image contour compression using
Ramer and Trapezoid methods.
The decomposition of Baby image using first
level of DWT is shown in Figure 10.
Figure 10: Baby image decomposition using first level of
DWT.
The compressed Baby image can be obtained
using approximation coefficients only as shown in
Figure 11 (related results are shown in the Table 3).
(a) (b)
Figure 11: Baby image reconstruction using
approximation coefficients: a) Original image, and
b) Compressed image.
First International Conference on Telecommunications and Remote Sensing
102

Table 3: Baby image results.
MSE PSNR [db] Bit Per
Pixel (bpp)
b)
15.86 36.13 2
The extracted contours using SSPCE method for
contour extraction of Baby image are obtained using
horizontal, vertical, and diagonal coefficients as
shown in Figure 12.
(a) (b)
Figure 12: Baby image: (a) Binary image from
details coefficients, and (b) Contours extraction
using SSPCE method.
The compressed contours for Baby image are
obtained using Ramer and Trapezoid methods are
shown in Figure 13(related results are shown in the
Table 4).
(a) (b)
(c) (d)
(e) (f)
Figure 13: Baby image contour compression using
Ramer and Trapezoid methods.
Table 4: Baby image results.
Measures
Method
(Compression)
MSE PSNR
[db]
CR Elapsed
Time
a) Ramer 0.0195 17.11 56.16 3.44
b) Trapezoid 0.019 17.08 56.51 2.88
c) Ramer 0.0216 16.45 62.32 3.17
d) Trapezoid 0.0216 16.65 62.32 2.77
e) Ramer 0.0263 15.80 75.88 2.98
f) Trapezoid 0.0263 15.80 75.88 2.56
The proposed algorithm is compared with binary
image which is obtained using suitable thresholding
criteria as shown in Figure 14 (related results are
shown in Figure 15 and in Table 5).
(a) (b)
Figure 14: Tools image: (a) Binary image using
threshold, and (b) Contours extraction using SSPCE
method.
Table 5: Tools image results ( Threshold).
Measures
Method
(Compression)
MSE PSNR
[db]
CR Elapsed
Time
a) Ramer 0.0183 17.38 69.47 9.89
b) Trapezoid 0.0182 17.39 69.36 9.13
c) Ramer 0.0207 16.84 78.82 8.59
d) Trapezoid 0.0205 16.88 78.06 8.09
e) Ramer 0.0236 16.27 89.84 7.04
f) Trapezoid 0.0236 16.28 89.67 6.58
Gray-Level Image Contours Extraction & Compression Using Wavelet Transform
103

(a) (b)
(c) (d)
(e) (f)
Figure 15: Tools image contour compression using
Ramer and Trapezoid methods (by threshold).
The results presented show that the proposed
algorithm has the best extraction property and
contour compression with better quality compared
with the binary image using threshold value. The
results show that SNR is improved by this algorithm
by about 0.2 decibels for some images.
6 CONCLUSIONS
The good quality of contour extraction and
compression are the main advantage of the proposed
algorithm compared with the binary image using
suitable threshold value. By using single level of
discrete wavelet transform the two sub-images are
obtained (compressed image and extracted contour).
Ramer and Trapezoid methods are used to compress
the extracted contours without significant visible
distortion.. The reconstruction quality improvement
of compressed contour about o.2 decibels. Important
advantage of the proposed method is the simplicity
of implementation both in terms of memory
requirement and fit criterion complication.
REFERENCES
Brigham, E.O., 1974. The Fast Fourier Transform,
Prentice-Hall, Englewood Cliffs.
Walsh, J., 1999. A closed set of normal orthogonal
functions. Amer. J. Math.
Clarke, R. J., 1985. Transform Coding of Images,
Academic Press.
Dziech, A., Belgassem, F., Nern, H. J., 2000. Image data
compression using zonal sampling and piecewise-
linear transforms. Journal of Intelligent And Robotic
Systems. Theory & Applications. Kluwer Academic
Publishers.
Dziech, A., Belgassem, F., Aboukhres, S., 1996. Periodic
Haar Piecewise Linear Transform. Proceedings of the
IMACS/IEEE-SMC Multiconference. Lile-France.
Ramer, U., 1972. An iterative procedure for the Polygonal
approximation of plane curves Computer Graphics
and Image Processing. Academic Press.
Vetterli, Martin, Kovacevic, 1995. Wavelets and Subband
Coding, Printice Hall Inc.
Dziech, A., Besbas, W., 1997. Fast Algorithm for Closed
Contour Extraction. Proc. of the Int. Workshop on
Systems, Signals and Image Processing.
Besbas, W., 1998. Contour Extraction, Processing and
Recognition, Ph.D Thesis. Poznan University of
Technology. Poznan.
Ukasha, A., Dziech, A., Elsherif, E., 2009. An efficient
method of contour compression. International
Conference on Visualization, Imaging and Image
Processing (IASTED/VIIP).
Ukasha, A., 2010. Arabic Letters Compression using New
Algorithm of Trapezoid method. International
Conference on Signal Processing, Robotics and
Automation (ISPRA'10).
Gonzalez, R. C., 1987. Digital Image Processing, Addison
Wesley, 2
nd
edition.
First International Conference on Telecommunications and Remote Sensing
104