
Soft Control of Swarms
Analytical Approach
Guillaume Sartoretti
∗
and Max-Olivier Hongler
STI/IMT/LPM,
´
Ecole Polytechnique F´ed´erale de Lausanne (EPFL), CH-1015, Lausanne, Switzerland
Keywords:
Rank-based Brownian Motions, Heterogeneous Autonomous Agents, Soft-control of Swarms, Exact Analytic
Solvable Models, Super-diffusive Shill Agent, Flocking.
Abstract:
We analytically study the collective dynamics of mutually interacting heterogeneous agents evolving in a
random environment. Our formal framework consists of a collection of N scalar drifted Brownian motions
(BM) diffusing on R. The mutual interactions are introduced via a ranked-based, real-time mechanism always
endowing the laggard (i.e the agent with the leftmost position) with an extra positive drift. The extra drift
generates a net tendency for any agents not to remain the laggard of the society. For well chosen individual
and extra laggard’s drifts, the agents organize with time to flock towards a tight and stable travelling spatial
pattern. For a population of (N −1) identical agents and an atypical fellow (called hereafter the shill), we are
able to analytically discuss the dynamics. In particular we exhibit how a single turbulent shill, stylized here
by a ballistic diffusion process, can destroy the cohesion of a swarm. Conversely, we also analytically show
how a single shill is able to safely pilot a whole swarm to avoid an obstacle, via interactions with its fellows.
A series of simulations experiments comfort our analytic findings.
1 INTRODUCTION
The capability of a collection of interacting stochas-
tic agents to exhibit an emergent collective behaviour
(i.e flocking behaviour) even in random environments
stimulates a strong research activity devoted to both
experimental and theoretical modeling approaches.
For suitable range of mutual interactions, flocking
(phase) transitions are observed, namely the self-
organized capability to create finite and persistent
spatio-temporal patterns (Banner A. D. and Karatzas,
2005; Yates C. A. and Sumpter, 2009; Chatterjee
and Pal, 2010; Dosseti, 2012; Pal and Pitman, 2008;
Ichiba T. and Fernhold, 2011; Bialek W. and Walczak,
2012).
Agents societies can be composed of either dy-
namically homogeneous or heterogeneous individu-
als requiring for each case drastically different ap-
proaches. For large and homogeneous population
of agents, the classical statistical mechanics concepts
and in particular the mean-field description (MF) di-
rectly offers an appropriate tool to analytically discuss
the global dynamics. In the MF description, one basi-
cally assumes that the behaviour of the global society
∗
Supported by the Swiss National Funds for Scientific
Research
can be characterized by the dynamics of a single rep-
resentative agent which feels its fellows’ interactions
via an effective external field. In most circumstances
however, homogeneity fails, and therefore a growing
attention is now paid to heterogeneous populations.
Heterogeneity occurs typically when one or several
masked agents, that we shall from now on refer to
as shills, exhibit leaders or troublemakers behaviours.
These shills are not recognized by the regular agents
which see them as ordinary fellows, leaving the inter-
action rules between them unchanged. The presence
of shills can strongly alter the ultimate evolution of
the whole society and it is the central goal here to an-
alytically study this problematic.
Our approach involves assemblies of interacting
stochastic agents in which a single shill exhibits a dif-
ferent individual behaviour. All agents, including the
shill, interact with their fellows with fixed given rules.
The paradigmatic vision of this situations has been
currently explored in ethology where one fake indi-
vidual is introduced among schools of fishes, cock-
roaches, newborn chicken, etc. The shill is able to
ultimately pilot the whole population (Gribovskiy A.
and Mondada, 2010; Faria J. J. and Krause, 2010;
Vaughan R. and Cameron, 2000). This basic mech-
anism also referred as the soft control of a popula-
tion (Han and Wang, 2010; Wang X. and Han, 2011;
147
Sartoretti G. and Hongler M..
Soft Control of Swarms - Analytical Approach.
DOI: 10.5220/0004176301470153
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 147-153
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Wang Y. and Liu, 2009; Wang and Guo, 2008) is the
core of our present paper. As heterogeneous societies
preclude MF approaches, rather few analytical results
are yet available. Recent mathematical models of het-
erogeneous rank-based interacting Brownian mo-
tions (RBM), introduced in finance (Banner A. D.
and Karatzas, 2005; Chatterjee and Pal, 2010; Pal and
Pitman, 2008; Ichiba T. and Fernhold, 2011), will be
used in the sequel to analytically approach the soft
control problematic. We shall analytically show how
a troublemaker can break the cohesion of an ini-
tially tight swarm and how a single agent can effi-
ciently incitate its fellows to achieve a preassigned
task.
Our paper is organized as follows: we first recall in
section 2 relevant properties of RBM, also known in
economy as the Atlas models. In section 3, we use
the RBM’s framework to show how a troublemaker
is able to smash an initially tight swarm. Our indi-
vidual dynamics are one-dimensional diffusion pro-
cesses with piecewise constant drifts except for the
shill, which will beassumed to be drivenby a ballistic
process with quadraticvariance in time. The ballis-
tic noise is itself generated by a simple non-Gaussian
diffusive stochastic process with nonlinear drift. In
section 4, we address the dual soft control problem in
which a shill is used to steer the whole collection of
RBM’s towards slots that are drilled through an ob-
stacle board.
2 RANK-BASED BROWNIAN
MOTIONS - ATLAS MODEL
Our approach makes extensive use of recent results
(Ichiba T. and Fernhold, 2011), that we now briefly
summarize. Let us consider a collection of N inter-
acting agents diffusing according to the class of pro-
cesses:
dY
i
(t) =
N
∑
k=1
g
k
1
Q
k
(i)
{Y (t)}+ γ
i
+ γ
!
dt+σ
i
dW
i
(t),
Y
i
(0) = y
i
, t ∈R
+
, (1)
where Y (t) = (Y
1
,Y
2
,··· ,Y
N
) ∈ R
N
and dW
i
(t) are
N independent standard White Gaussian Noise pro-
cesses (WGN) processes. The indicator function 1
Q
k
in Eq.(1) effectively generates mutual interactions.
The effective, time-dependent drift component g
k
en-
tering into the drifts (g
k
+ γ
i
+ γ) of the N Brown-
ian motions on R, is rank-based. Namely, it is in-
stantaneously adjusted according to the position (i.e.
the rank) occupied by each agent with respect to
the remaining (N − 1) fellows. The constant drift
components γ
i
are name-based, i.e. they are defi-
nitely assigned to each individual agent (γ
i
is time-
independent). Finally, a constant drift component γ
can be added, which is common to all agents. Ac-
cordingly Eq.(1) describes a collection of N diffusion
processes having piecewise deterministic drifts. The
somehow simpler situation obtained when γ
i
≡ 0 ∀i
has been thoroughly studied (Pal and Pitman, 2008).
In the sequel and without loss of generality, we sys-
tematically choose γ to be the (average) barycentric
speed of the swarm. This is achieved, provided one
has:
N
∑
k=1
[g
k
+ γ
k
] = 0. (2)
For future use, we introduce the following notations
and definitions:
1. We write
¯
Y (t) =
1
N
N
∑
k=1
Y
k
(t),
¯
Y ∈ R, (3)
for the barycenter position. The set Σ
N
stands for
the set of all the permutations of {1, 2, ...,N}. It
is proven (Ichiba T. and Fernhold, 2011) that, for
almost every initial conditions and when the set of
constraints
l
∑
k=1
g
k
+ γ
p(l)
< 0 (4)
are fulfilled for all possible permutations p =
(p(1),..., p(N)) ∈ Σ
N
, then the N deviations pro-
cesses:
˜
Y
i
(t) = [Y
i
(t) −
¯
Y (t)] (5)
converge to stationary probability measures. Note
that Eq.(4) yields therefore a set of (N −1) ×
|Σ
N
| = N! (N −1) constraints to be verified.
2. When all constraints in Eq.(4) are fulfilled, the dy-
namics given by Eq.(1) then converges to a tight
swarm described by a stationary multi-variate
process characterizing the (N −1)-gap processes
Ξ
i
(t) = [Y
i+1
(t) −Y
i
(t)]. (6)
The associated probability density ψ(z), z ∈R
N−1
+
can be written as a sum-of-product-of-exponential
form:
ψ(z) =
∑
q∈Σ
N
N−1
∏
k=1
λ
−1
p,k
!
−1
∑
p∈Σ
N
exp(−hλ
p
,zi)
(7)
with the parameters explicitly given by
λ
p
=
λ
p,k
N−1
k=1
λ
p,k
=
−4
k
∑
l=1
g
l
+ γ
p(l)
σ
2
k
+ σ
2
k+1
. (8)
Remark. It is worth observing that the diffusion co-
efficients σ
i
do not enter into the set of tightness con-
straints given in Eq.(4). However, the σ
i
’s do enter
into the parameters Eq.(7) characterizing the station-
ary probability measure.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
148

3 HOW DOES A
SUPER-DIFFUSIVE FELLOW
SMASH TIGHTNESS
We first investigate how a single ”turbulent” fellow
can destroy the cohesion of a tight swarm. To this
aim, we use the RBM formalism introduced in section
(2). We consider a configuration involving (N −1)
identical mutually interacting RBM’s, referred from
now on as the regular agents, interacting with a sin-
gle fellow, the shill, say agent number one, which is
itself driven by a ballistic diffusion process (remem-
ber from Eq.(1) that the (N −1) regular agents are
drivenby independent WGN’s). The ballistic process,
to be introduced below, exhibits a variance ∝ t + βt
2
with a ballistic parameter β ≥ 0 a constant. For
β = 0, the shill simply behaves as a regular fellow
and therefore, in this β = 0 limit, our global dynamics
reduces to a standard version of Eq.(1). We set the
specific parameters: g
N
= (N −1)g and g
k
= −g for
1 ≤ k ≤ N −1. In addition, we shall further assume
that:
i)
∑
N
i=1
γ
i
= 0,
ii) max
1≤i≤N
γ
i
< g.
The couple of constraints i) and ii) imply that the
Eq.(4) is fulfilled. Indeed, we directly verify that :
−g+ γ
p(1)
< 0, −2g+ γ
p(1)
+ γ
p(2)
< 0, ···
−(N −1)g+
N−1
∑
k=1
γ
p(k)
< 0. (9)
Hence, for β = 0, our collection of agents behaves
as a tight swarm enjoying a stationary joint proba-
bility law for the inter-distance between successive
agents.
Let us now focus on β > 0. Now, the shill Y
1
(t) be-
haves as a turbulent fellow which interact with the
remaining (N −1) regular fellows. Specifically the
dynamics of Y
1
(t) is chosen to be described by:
dY
1
(t) =
N
∑
k=1
g
k
1
Q
k
(i)
{Y (t)}+ γ
1
+ γ
!
dt + dZ(t) ,
Y
1
(0) = y
1
t ∈ R
+
, (10)
where the process dZ(t) is a super-diffusive bal-
listic noise generator introduced in (Hongler M. O.
and Blanchard, 2006; Hongler M. O. and Rodriguez,
2012):
dZ(t) = {βtanh[βZ(t)]}dt + dW (t), Z(t = 0) = 0.
(11)
The non-Gaussian Markov diffusion process Z(t)
given in Eq.(11) is fully characterized by its transition
probability density P
±
(z,t | 0) which simply reads:
P
±
(z,t | 0) =
P
+
+ P
−
(z,t | 0)
2
=
e
−
β
2
2
t
√
2πt
e
(x±βt)
2
2t
,
(12)
with average hZ(t)i = 0 and variance hZ
2
(t)i = t +
β
2
t
2
.
The simple form given in Eq.(12) suggests the exis-
tence of an alternative representation for the ballistic
noise Z(t). Indeed, writing BM
±β
(t) for the Brown-
ian motions with ±β constant drifts, we observe that
the transition probability for the process Z(t) can be
rewritten as Z(t) = B BM
±β
(t) where B is a symmet-
ric Bernoulli r.v., taking the values ±1 with equal
probability 1/2. Hence, one realisation of the Z(t)
consists first in choosing with probability 1/2 one
among the couple processes BM
±β
(t), and then fol-
low the realisation of the selected process (see ex-
ample 2 in (Rogers and Pitman, 1981) and (Hongler
M. O. and Blanchard, 2006; Hongler M. O. and Ro-
driguez, 2012)).
We now come back to the dynamics jointly involv-
ing a turbulent fellow given by Eq.(10) and (N −1)
regular agents described by Eq.(1). We then view the
(N −1) regular agents as being infiltrated by a the
shill Y
1
(t).
Now we have to investigate the values of β enabling
the swarm to remain tight (i.e. if a stationary prob-
ability measure for the intervals between successive
agents exists). In view of the representation given in
Eq.(12), for each realisation of the noise source Z(t),
we effectively deal with a standard RBM model with
a re-normalized name-based drift of Y
1
(t), namely
γ
1
7→ γ
1
±β depending on the outcome of B . Accord-
ingly, to infer on the tightness of the swarm, we sim-
ply have to separately examine Eq.(4) for the couple
of outcomes ±β.
Realisation +β. Let us define γ =
β
N
, γ
1
=
N−1
N
β
and γ
i
= −γ = −
β
N
for 2 ≤ i ≤N. The constraints
Eq.(6) are required for the swarm to be tight. This
yields, for l = 1 and p = (1,2,3...,N), to the most
critical constraint:
g
1
+ γ
p(1)
< 0 ⇒ −g+
N −1
N
β < 0
⇔ β <
N
N −1
g. (13)
Provided that Eq.(13) holds, the swarm remains
tight when the Z
t
noise induces a +β extra drift.
Realisation −β. The same reasonning applied to
the −β case yields:
γ = −
β
N
γ
1
= −
N −1
N
β γ
i
=
β
N
(2 ≤ i ≤ N) .
(14)
SoftControlofSwarms-AnalyticalApproach
149

The critical constraint arises when l = 1 and γ
p
:=
β
N
,...,
β
N
,−
N−1
N
β
with:
−g+
β
N
< 0 ⇔ β < N ·g. (15)
This implies that for β < N ·g, the swarm remains
tight when the Z
t
noise induces a −β extra drift.
The previous considerations can be summarized by
observing that when the constraints Eq.(13) are ful-
filled, so are also those given in Eq.(15). This
suggests to distinguish an alternative “semi”-tight
regime which arises when the constraints Eq.(15)
alone are fulfilled. In this “semi”-tight case, the
swarm exhibits a tight configuration when the −β re-
alisation is achieved and is nottight for the other alter-
native +β. This intrinsic asymmetry can be easily un-
derstood as our RBM dynamics only pushes the lag-
gard towards the others. Hence, regarding the tight-
ness, the shill is obviously less influential when the
−β extra drift is realised.
3.1 Spatial Dispersion of the Agents
The extra ±β-drifts due to the super-diffusive process
driving the shill dynamics obviously affect the spatial
dispersion of the swarm. As all noise sources (includ-
ing the dZ(t) process) have zero average, the barycen-
ter of the whole population will remain unchanged by
the presence of dZ(t). However, due to the presence
of the shill, an initial single-modal cluster of agents
will, as time increases, be split into two separately
evolving population subgroups. According to the ±β
realisation taken by dZ(t), the overall effect of the
shill will steer the swarm either towards the negative
or positive direction; this generates the formation of
two distinct clusters. Each cluster has an individual
barycentricvelocity: γ =
γ
1
N
=
±β
N
; this guaranteesthat
the average barycenter remains unchanged.
Specifically, whenever the shill’s drift assumes the
value −β, the shill has an overall propensity to stay at
the rear of the swarm. Accordingly, all regular agents
will, with high probability, be endowed with the rank-
based drift −g. Hence the regular agents possess a
clear tendency to be driven toward the negative direc-
tion on R. Conversely, in presence of the +β reali-
sation, the shill is very likely to belong to the group
of leaders. This imposes to the remaining (N −1)
regular fellows to equally share, with alternations, the
rank-baseddrift of (N −1)g which drives the laggard.
Therefore, with the +β realisation, the whole popu-
lation is driven towards the positive direction of R.
We now can isolate three regimes depending on the
strength β.
a) β < β
c
:=
N
N−1
g. In this regime, the shill is able
to steer the whole population in one of the two
possible directions while remaining itself attached
to the swarm. In other words, a stationary proba-
bility measure exists for the distance between the
agents (i.e. all agents evolve in a single flock).
Note however that the presence of the shill breaks
an initially uni-modal spatial repartition into a bi-
modal repartition.
For three agents (i.e. one shill and two regular
fellows), the resulting spatial repartition obtained
by simulation is shown in Figure (1). In Figures
(1) and (2), the shill’s position is represented in
black, the others being displayed in grey.
Figure 1: Probability of spatial repartition of the agents at
t
end
= 10, numerical computation over 10
3
runs, with N =
3, g = 1, β = 1.1 < β
c
=
3
2
.
b) β
c
≤β < g·N. Here the strength of the ballistic
noise precludes to reach a global stationary state
for the inter-distance processes between the N
agents. Indeed, the remormalized drift associated
with the +β realisation of dZ(t) (i.e.
ˆ
γ
1
= γ
1
+ β),
violates the constraint Eq.(13). However, for the
−β realisation, the constraint for
ˆ
γ
1
= γ
1
−β is ful-
filled, implying that the shill remains flocked with
its (N−1) remaining fellows. An experimentwith
β chosen in this range, shows the spatial reparti-
tion in Figure (2) (left).
Figure 2: Left: End position distribution at t
end
= 10, with
N = 3, g = 1, β = β
c
= 1.5.
Right panel: Probability density of the position at t
end
= 10
for N = 3, g = 1, β = 4 > N ·g. Both numerical computa-
tions include 10
3
runs.
c) Finally, for β > g·N, the shill becomes highly
turbulent and the tightness constraints are never
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
150

fulfilled. The shill escapes from the flock and the
resulting spatial repartition is typically shown in
Figure (2) (right).
For all choices of the ballistic strength β, the numeri-
cal results intimately match the analytical predictions.
In particular, the shill escapes from the flock when the
critical ballistic strength β = β
c
is reached (for the +β
realisation, or when β = N ·g for the −β realisation
of dZ(t). In these non-stationary regimes, the shill
quits the (N −1)- regular tight swarm with velocity
V (β) ∝ β.
3.2 Distance between Successive Agents
Complementary to the tightness constraints, let us
now briefly discuss the stationary probabilitymeasure
which characterizes the distances between successive
agents. To this aim, we shall choose β to ensure the
existence of a global stationary regime (i.e. ensures
tightness), namely 0 ≤β < β
c
=
N
N−1
g.
Note however that using the results derived in
(Ichiba T. and Fernhold, 2011), heterogeneous dif-
fusion constants can also be analytically discussed.
The distances separating consecutive agents defined
in Eq.(6) can be explicitly computed by using the re-
sults summarized in section (2). For agent Y
1
(t) and
in view of the extra β-drift induced by the shill bal-
listic driving, we are now led to define a couple of
name-based drifts vectors as:
γ
±
= ±
N−1
N
β −
β
N
··· −
β
N
. (16)
The fulfillment of the tightness constraints given in
Eq.(4) ensures that the λ
p,k
from Eq. (8) are strictly
positive (∀p,k). Hence, it results a couple of sta-
tionary probability densities (one for each realisation
+β and −β), characterizing the inter-distance process
Ξ(t) (see Eq.(6)):
P {z ≤Ξ(t) ≤ z+ dz — ±β is realised}= P
±β
(z)dz
=
∑
p∈Σ
N
N−1
∏
k=1
λ
±
p,k
!
−1
−1
∑
p∈Σ
N
exp
−
λ
±
p
,z
dz.
(17)
The complete stationary probability density then
reads:
P (z) =
1
2
P
+β
(z) + P
−β
(z)
. (18)
4 USING A SHILL TO GUIDE
THE COLLECTIVE CROSSING
OF OBSTACLES
The shill Y
1
(t) of section (3) has so far been viewed
as a mere trouble maker. However, for specific tasks
to be achieved, a shill’s presence might become truly
beneficial. Indeed, the presence of a shill can softly
control a swarm towards a preassigned target.
To concretely illustrate this alternative view point, let
us, once again, consider a collection of (N −1) iden-
tical drifted Brownian (regular) agents and one shill,
say Y
1
(t), all diffusing on R. From now on, we shall
represent the evolution on R
2
with the time being
identified with the x-axis, and positions with the y-
axis. At time t = 0, all N agents start at location
y
i
(0) = 0, 1 ≤ i ≤ N. We may think of agents running
on the x-axis with constant unit speed, as we therefore
identify the x-axis with time. At the x-location T (see
Figure 3), we introduce a solid wall (i.e. the obstacle)
in which two-slots are drilled. The global objective
for the N agents is to try to avoid the fatal collisions
with the wall by traveling trough one of the couple of
slots. The two slots have width W and are symmetri-
cally drilled at the ordinates ±D, see Figure (3) for a
sketch of the configuration.
Figure 3: Initial configuration for the soft control problem.
The agents start their diffusion at (t
0
,y
0
) = (0,0).
In absence of shill, one has an homogeneous swarm
(all agents are dynamically identical) and the N-
swarm proceeds according to the rule defined in
Eq.(1). As a consequence, the wall will be hit with
high probability as, at time T, the probability den-
sity of the positions will be given by a collection of
N centered Gaussians (we basically have N Brow-
nian motions with constant drifts having their mean
barycenter located at zero). As seen in section (3), the
presence of a super-diffusive shill Y
1
(t) may strongly
modify this nominal β = 0 picture. IndeedY
1
(t), with
suitable parameters β and g is able to steer the whole
swarm with high preference to one of the slots. This
basic and simple idea can be made fully quantita-
tive as discussed below. In our simulations, we set
β = 0 once the slots are crossed. Therefore, the global
swarm continues its nominal path with a tight config-
uration after the obstacle.
4.1 Optimal Barycentric Driving for
Suitable Choice of β
First, we select the Y
1
(t) parameters to ensure global
SoftControlofSwarms-AnalyticalApproach
151

tightness. This is achieved by defining β < β
c
=
N
N−1
g. For a single realisation of the Z(t) noise, we
already know that the average barycentric y-speed of
the swarm is
±β
N
. Hence, at time T, thegroup barycen-
ter reaches the y-position located at
±βT
N
. The center
of the slots being located at ±
D+
W
2
, we therefore
naturally require:
±βT
N
= ±
D+
W
2
⇔ β
opt
:=
D+
W
2
·N
T
.
(19)
The choice β
opt
, doesnot yet ensurethat the shillY
1
(t)
itself remains attached to the flock. This second re-
quirement can be achieved provided one has:
D+
W
2
·N
T
= β
opt
< β
c
=
N
N −1
g
⇔ g >
D+
W
2
·(N −1)
T
=: g
c
. (20)
This choice of the couple parameters β
opt
and g > g
c
now jointly ensures that i) the barycenter is steered
towards one of the slots centers and ii) Y
1
(t) remains
tightly attached to the swarm. The overall swarm’s
y-dispersion is itself dependent on the diffusion con-
stants σ
i
, which were here taken as (σ
i
:= σ ∀i).
Figure 4: Left panel: N = 10 agents, W = 20 and D = 10.
Right panel: N = 20 agents, W = 20 and D = 50.
4.2 Adjusting the Spatial Dispersion
Resolution for a Given Drift g
When the drift g is fixed, the ballistic component β
cannot always be chosen to simultaneously ensure
tightness and the collective drive into one of the slots.
Keeping the barycentric driving β = β
opt
, as defined
in Eq.(19), three different scenarii are now possible:
a) β = β
opt
< β
c
. In this case, the shill nicely
steers the group towards one of the slots while
staying attached to the flock, as we already estab-
lished in section 4.1.
b) β = β
opt
≥ β
c
. Here, Y
1
(t) escapes from the
(N − 1)-flock with a constant drifting velocity.
Two sub-cases have to be distinguished, i) drift
β−g resulting when +β is realised by dZ(t) and
conversely ii) drift (N −1)g−β for the alternative
−β case. In both cases, the regular agents evolve
with an average drift γ
ave
which reads:
γ =
(
β
N
=
(β−g)·1+(N−1)·γ
ave
N
for +β
−
β
N
=
((N−1)g−β)+(N−1)γ
ave
N
for −β
⇔ γ
ave
=
g
N−1
−g
.
(21)
c) β = β
opt
≥β
c
< N ·g. Here, the shill remainsat-
tached to the flock for the −β realisation of dZ(t),
but escapes otherwise. This then leads to a mix of
cases a) and b) depending on whether +β or −β
is realised.
The computation of γ
ave
from case b) shows that with
g fixed such that β
opt
≥ β
c
, the shill escapes from the
flock (hence, no stationary probability measure ex-
ists). The remaining (N −1) regular fellows evolve
with average speed γ
ave
(which is β-independent).
Whatever the values taken by β, the shill is never
able to drive the swarm through one of the slots, the
swarm’s speed being only g-dependent if the shill is
not attached to the swarm.
So far, only the swarm’s directions has been con-
sidered. Obviously, the dispersion is also a determi-
nant feature for efficient slots crossings. Here, not
only g but the ratio
g
σ
will be determinant. Clearly
for small g values, the swarm dispersion will exhibit
a clear tendency to exceed the slots widths, altering
therefore the overall efficiency.
4.3 Multi-slots Configurations
So far, we did consider the capability of a shill to steer
the swarm through a couple of slots. For multi-slots
configurations, the shill construction used before nat-
urally suggests to define more general shills to steer
swarms in many different directions. This is achiev-
able by replacing the ballistic noise driving the shill
with more complex stochastic processes. Doing so
however, the shill dynamics cannot be anymore rep-
resented by a simple diffusive stochastic differential
equation like Eq.(11). As an illustration, consider a
three symmetrical slots configuration for which one
is naturally driven to introduce the following noise
source:
dZ(t) =
(
βtanh(βZ(t))dt + dW (t) with prob.
2
3
,
dW (t) with prob.
1
3
.
(22)
The shill dynamics is taken as before, namely with
probability
2
3
it steers the swarm towards the positive
or negative slots with ballistic parameter β and with
probability
1
3
, it behaves as a regular agent driving the
swarm on a centered path, see Figure (5).
For arbitrary number of slots and configurations, one
can generalize our construction by suitably adjusting
the properties of the noise source driving the shill.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
152
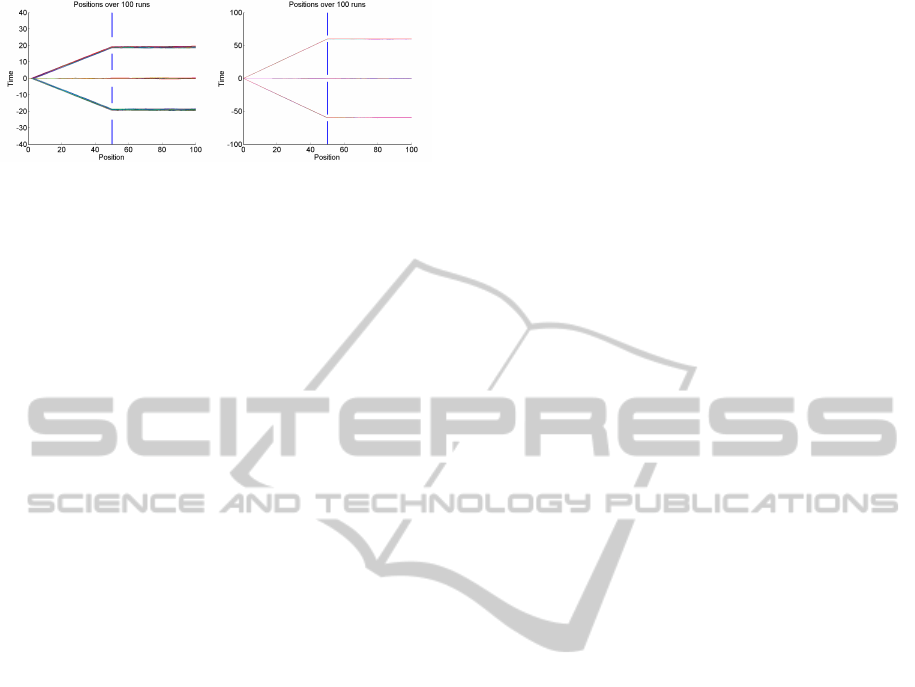
Figure 5: Trajectories for β and g optimal, with N
d
= 3
doors, under different conditions for the position/width of
the doors.
5 CONCLUSIONS
It is a true challenge, to analytically discuss the swarm
dynamics of heterogeneous interacting agents. Due to
heterogeneity, ordinary analytical tools like the mean-
field approach are to be ruled out a priori. Hence be-
sides simulation experiments, very little hope remains
for rigorous theoretical results. We think particularly
to modeling approaches relying on statistical mechan-
ics and phase transitions to explain the emergence of
self-organized spatio-temporal patterns (i.e flocking).
Howeveras ourpaper intends to show, facing inhomo-
geneous swarms problems, complete hope for analyt-
ical results should not be abandoned. The theoretical
analysis, when achievable, definitely offers sources of
inspiration for new and unexpected research axis.
In our present contribution, we barely scratched
the wealth of analytical possibilities. Indeed, swarm
heterogeneity has numerous origins, affecting the in-
dividual drifts and/or the variances, modeling the sen-
sitivity of each agent to the external random environ-
ment. In parallel, heterogeneity can either be sys-
tematic, thus implying that each agent behaves dif-
ferently, or can be limited to one or only a few indi-
viduals who exhibit singular behaviors. In the latter
configuration, the emergent swarm dynamics can be
affected, sometimes even strongly, by the exotic be-
havior of this (or these) individual(s). The influence
of the exotic fellow(s) can hence be viewed as a soft
control mechanism, either harmful or beneficial. The
exotic insiders, acting as leaders (or as shills in econ-
omy) are not detected to be singular by the other fel-
lows, offering the (politically frightening possibility!)
to drive large swarms towards global goals known
only to the manipulators. A formal analytical ap-
proach (complemented with simulations) to this gen-
eral problematic is a truly fascinating challenge.
Further works include analysis of multiple shills
influence, leading to the separation of the initial
swarm into multiple flocks, one shill soft-controlling
each flock. Generalisation in two or three dimensions
would also provide more realistic applications.
REFERENCES
Banner A. D., R. F. and Karatzas, I. (2005). Atlas models
of equity markets. Ann. Appl. Prob. 15, 2296-2330.
Bialek W., Cavagna A., G. I. M. T. S. E. M. V. and Walczak,
A. M. (2012). Statistical mechanics for natural flocks
of birds. PNAS 13, vol. 109, 4786-4791.
Chatterjee, S. and Pal, S. (2010). A phase transition
behaviour for brownian motions interacting through
their ranks. Prob. Theory Relat. Fields 147, 123-159.
Dosseti, V. (2012). Cohesive motion in one-dimensionnal
flocking. Physica A: Math. Theor. 45.
Faria J. J., Dyer J. R. G., . . . and Krause, J. (2010). A novel
method for investigating the collective behaviour of
fish: Introducing ’robofish’. Behavioral Ecology and
Sociobiology 8, vol. 64, 1211-1218.
Gribovskiy A., Halloy J., D. J. L. H. B. and Mondada,
F. (2010). Towards mixed societies of chickens and
robots. IEEE/RSJ 2010 International Conference on
Intelligent Robots and Systems, Conference Proceed-
ings pp. 4722-4728.
Han, J. and Wang, L. (2010). New strategy of the shill:
Consistent moving. Proceedings of the 29th Chinese
Control Conference, pp. 4459-4464.
Hongler M. O., Filliger R., P. B. and Rodriguez, J. (2012).
”Contemporary Topics in Mathematics and Statis-
tics with Applications” in ”On Stochastic Processes
Driven By Ballistic Noise Sources”. Ed. M. R. Ad-
hikari.
Hongler M. O., R. F. and Blanchard, P. (2006). Solu-
ble models for dynamics driven by a super-diffusive
noise. Physica A 370, 301-355.
Ichiba T., Papathanakos V., B. A. I. K. and Fernhold, R.
(2011). Hybrid atlas model. Ann. Appl. Prob. 21(2)
609-644.
Pal, S. and Pitman, J. (2008). One dimensional brownian
particles with rank-dependent drifts. Ann. Appl. Prob.
18 2179-2207.
Rogers, L. C. G. and Pitman, J. W. (1981). Markov func-
tions. Ann. of Prob. 9(4), 573-582.
Vaughan R., Sumpter N., H. J. A. F. and Cameron, S.
(2000). Experiments in automatic flock control.
Robotics and Autonomous Systems 1, vol. 31, 109-
117.
Wang, L. and Guo, L. (2008). Robust consensus and soft
control of multi-agent systems with noises. Journal of
Systems Science and Complexity 3, vol. 21, 406-415.
Wang X., J. H. and Han, H. (2011). Special agents can
promote cooperation in the population. PLoS ONE
12, vol. 6.
Wang Y., X.-Z. M. and Liu, J.-P. (2009). Soft control for
swarm systems with simple attraction and repulsion
functions. Proceedings of the 2nd International Con-
ference on Intelligent Networks and Intelligent Sys-
tems, pp. 482-485.
Yates C. A., Erban R., . . . and Sumpter, D. J. T. (2009).
Inherent noise can facilitate coherence in collective
swarm motion. PNAS 14, vol. 106, 5464-5469.
SoftControlofSwarms-AnalyticalApproach
153
