
Synchronizing for Performance
DCOP Algorithms
∗
Or Peri and Amnon Meisels
Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84105, Israel
Keywords:
Distributed Search, DCOP.
Abstract:
The last decade has given rise to a large variety of search algorithms for distributed constraints optimization
problems (DCOPs). All of these distributed algorithms operate among agents in an asynchronous environment.
The present paper presents a categorization of DCOP algorithms into several classes of synchronization. Al-
gorithms of different classes of synchronization are shown to behave differently with respect to idle time of
agents and to irrelevant computation. To enable the investigation of the relation between the classes of syn-
chronization of algorithms and their run-time performance, one can control the asynchronous behavior of the
multi-agent system by changing the amount of message delays. A preliminary probabilistic model for com-
puting the expected performance of DCOP algorithms of different synchronization classes is presented. These
expectations are realized in experiments on delayed message asynchronous systems. It turns out that the per-
formance of algorithms of a weaker synchronization class deteriorates much more when the system becomes
asynchronous than the performance of more synchronized DCOP algorithms. The notable exception is that
concurrent algorithms, that run multiple search processes, are much more robust to message delays than all
other DCOP algorithms.
1 INTRODUCTION
Distributed constraint optimization problems
(DCOPs) are composed of agents, each holding its
local constraints network, that are connected by con-
straints among variables of different agents. Agents
assign values to variables, attempting to generate a
globally optimal assignment, minimizing the sum
of costs of constraints between agents (cf. (Meisels,
2008; Modi et al., 2005; Yeoh et al., 2010)). To
achieve this goal, agents check the value assignments
to their variables for costs and exchange messages
with other agents, to check the overall costs of their
proposed assignments against the value of constraints
with variables owned by different agents (Modi et al.,
2005; Yeoh et al., 2010; Gershman et al., 2009).
A search procedure for an optimal assignment
of all agents in a Distributed Constraints Optimiza-
tion Problem (DCOP) is a distributed algorithm. All
agents cooperate in search for a globally optimal so-
lution. The search procedure involves assignments of
all agents to all their variables and the exchange of
∗
Supported by the Lynn and William Frankel center for
Computer Sciences and the Paul Ivanier Center for Robotics
and Production Management.
messages among agents, to check the global cost of
assignments arising from constraints between agents.
DCOP algorithms differ greatly in their design. The
present study defines classes of synchronization for
DCOP algorithms. Each class is based on specific
conditions that are proven to hold for any agent that
performs an algorithm of the correlative synchroniza-
tion class.
Computations of agents during search are aimed
at one of two complementary goals. Either prove that
some partial assignment can be consistently extended
by additional assignments of the computing agent to
its variables, or prove that the partial assignment can-
not be extended in this way (and therefore cannot be
extended to a complete solution). Either of these two
options advances the complete search process. The
former extends the search process and delivers the
new partial assignment to an unassigned agent. The
latter prunes the subtree under the current view, trig-
gers a backtrack and as a result the search process
moves to a different part of the search tree.
Any subtree that does not contain a solution can in
general be proven to be so in more than one way and
by more than one agent. Asynchronous algorithms
enable the proofs to be given concurrently by multi-
5
Peri O. and Meisels A..
Synchronizing for Performance - DCOP Algorithms.
DOI: 10.5220/0004179100050014
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 5-14
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

ple agents (Bessiere et al., 2005; Modi et al., 2005). A
central idea of the present study is that one can think
of additional such proofs if they are computed non-
concurrently as irrelevant computations. The empha-
sis on the non-concurrency of the different compu-
tations of the same proof is important, because con-
current computations do not necessarily lengthen the
non-concurrent run-time of the algorithm (Meisels,
2008; Zivan and Meisels, 2006c). Completely syn-
chronous DCOP algorithms can be shown to guaran-
tee that such irrelevant computations will never hap-
pen during search. However, the price paid by typ-
ical synchronous DCOP algorithms is the fact that
all computations happen sequentially and therefore
all computations contribute to the non-concurrent run
time of these algorithms.
The categorization of algorithms is based on the
amount of enforced coordination needed to make a
decision of a value assignment. We show that, typi-
cally, synchronization results with idle-time, as agents
are compelled to wait for their peers’ actions before
taking action. On the other hand, attempts to uti-
lize the system’s idle-time by allowing agents to as-
sign their variables without coordinating (e.g. asyn-
chronously) is shown to create irrelevant computa-
tion, some at the expense of idle-time as intended, but
some can potentially lengthen the total run-time. The
focal point of the present paper is the investigation of
these two attributes of DCOP algorithms: the amount
of idle time vs. irrelevant computation.
The asynchronous nature of a system that can be
parametrized by the amount of delay of messages di-
rectly affects the amount of irrelevant computation.
The amount of irrelevant computation may deterio-
rate the run-time performance of an asynchronous al-
gorithm. This impact is analyzed for a synchronous
and a less synchronous protocol under different sys-
tem conditions. In contrast, a Conc mechanism which
incorporates several synchronous search-processes is
shown to shorten the idle-time imposed by a syn-
chronous algorithm without inflicting irrelevant com-
putation and is thus both more efficient and more re-
sistant to system conditions.
Distributed constraints optimization problems
(DCOPs) are presented in Section 2. Section 3
presents classes of synchronization for DCOP search
algorithms and classifies several well known algo-
rithms into these classes. All categorized DCOP algo-
rithms are treated in three groups - DCOP algorithms
that use a DFS tree (Modi et al., 2005; Chechetka
and Sycara, 2006; Yeoh et al., 2010); algorithms
that do not use a DFS tree (Gershman et al., 2009);
and algorithms that incorporate multiple search pro-
cesses (Meisels, 2008; Netzer et al., 2010). The
computation of expected idle time for different algo-
rithms, as a function of their synchronization class is
presented in Section 4, along with a general proba-
bilistic model of asynchronous idle time. The com-
putation of the expected idle time is also presented
in section 4. An extensive experimental evaluation,
which compares the behavior of several DCOP algo-
rithms in the presence of message delays is in Sec-
tion 5. The results of the evaluation supports our the-
sis and theoretical analysis that claims that a strongly
coordinated algorithm is more efficient than a weakly
coordinated one. Interestingly, this holds in a com-
pletely asynchronous system. It also demonstrates the
impact of the degree of the asynchrony of the sys-
tem over the synchronous, asynchronous and ’Conc’
mechanisms. Section 6 discusses the experimental
behavior of the algorithms and a possible explana-
tion for the outstanding performance and robustness
of concurrent DCOP algorithms.
2 DISTRIBUTED CONSTRAINT
OPTIMIZATION
A DCOP is composed of a set of n agents
A
0
,A
2
,...,A
n−1
, along with a set {X
i
j
: 0 ≤ i ≤
n − 1,1 ≤ j ≤ k
i
} of constrained variables. Each
agent A
i
is responsible for assigning the variables
X
i
1
,X
i
2
,...,X
i
k
i
. A constraint or relation C is a func-
tion (typically termed the “cost” or the “gain”) from
a subset of the Cartesian product of the domains of
the constrained variables that assumes real values.
For a set of constrained variables X
1
,X
2
,...,X
l
, with
corresponding domains of values for each variable
D
1
,D
2
,...,D
l
, the constraint is a function C : D
1
×
D
2
× · · · ×D
l
−→ R
+
to the non-negative reals. A bi-
nary constraint C
i j
between any two variables X
j
and
X
i
is a function from a subset of the Cartesian product
of their domains; C
i j
: D
i
× D
j
−→ R
+
. We denote
that two variables X
i
,X
j
share a constraint by C
i j
∈ C.
In a distributed constraint optimization prob-
lem, constrained variables may belong to different
agents (Modi et al., 2005; Gershman et al., 2009).
Each agent has a set of constrained variables, i.e., a
local constraint network.
An assignment is a pair < var,val >, where var
is a variable of some agent and val is a value from
var’s domain that is assigned to it. A compound label
(or a partial solution) is a set of assignments of values
to a set of variables. A feasible solution is a com-
pound label assigning values to all variables. An op-
timal solution P of a DCOP is a feasible solution, that
has a minimal global cost (or a maximal global gain)
for all the constraints. Agents check assignments of
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
6

values against non-local constraints by communicat-
ing with other agents through sending and receiving
messages. Agents exchange messages with their con-
strained agents whose assignments have a cost that
arises from constraints (Bessiere et al., 2005). Agents
connected by constraints are therefore called neigh-
bors. The ordering of agents is termed priority, so
that agents that are later in the order are “lower prior-
ity agents” (Yokoo, 2000; Bessiere et al., 2005).
The following simplifying assumptions are rou-
tinely made in studies of DCOPs and are assumed
to hold in the present study (Yokoo, 2000; Bessiere
et al., 2005):
(1) Each agent holds exactly one variable.
(2) Messages arrive at their destination in finite time.
(3) Messages sent by agent A
i
to agent A
j
are received
by A
j
in the order they were sent.
3 FORMAL ELEMENTS OF
SYNCHRONIZATION
The intuitive notion of classes of synchronization for
different DCOP algorithms is based on certain state-
ments of partial consistency that the states of the algo-
rithms guarantee. The following definitions of consis-
tency states of DCOP algorithms relate to the idea of
a search tree. A search tree is defined for a distributed
search process as follows.
Definition 1. The Search Tree(ST) of a DCOP algo-
rithm is defined by a linear ordering of the agents
A
0
,...,A
n−1
of the DCOP. This order defines a tree
where each node at some level i, (0 ≤ i < n) represents
a partial assignment of A
0
,...,A
i−1
and each edge di-
verging from such a node adds a possible assignment
of a value v
i
of A
i
(v
i
∈ D
i
, where D
i
is the domain of
values of agent A
i
) to the partial assignment.
A search process over a ST is the following
Definition 2. A Search Process(SP) of a DCOP is a
distributed computation (composed of local computa-
tions by agents and of message passing among them)
that scans some subtree of the problem’s search-tree
in search of the lowest cost global assignment.
Typically, search processes attempt to find a par-
tial assignment such that the sum of costs of the con-
straints among assigned agents in the partial assign-
ment is less than or equal to some Upper-Bound:
∑
c
i j
∈C
C(i, j) ≤ UB.
Now one can define the concept of a backward-
consistent view of an agent
Definition 3. Agents have views of assignments of
agents that are ordered before them on the search
tree. The view of agent A
i
, of a DCOP search-process,
is said to be Backwards-Consistent(BC) if for every
agent A
j
that is before A
i
in the search tree (i.e., j < i
and C
i j
∈ C) that appears in A
i
’s view it is the case
that
∑
j
l=0
∑
k<l,c
kl
∈C
C(k,l) ≤ UB.
In other words, a view of agent A
i
that is
backwards-consistent contains a partial-assignment
of agents ordered before A
i
whose total cost is not
higher than the Upper-bound. In an asynchronous
system, UB in definition 3 relates to the upper bound
known to agents that are incorporated in A
i
’s view, as
they send their assignment states to A
i
. In an anal-
ogous way to definition 3 one can define a forward
consistent view, where the partial assignment is con-
sistent forward with unassigned agents.
Definition 4. The view of agent A
i
, of a DCOP
search-process, is said to be Forward-Consistent(FC)
if for every agent A
j
that is before A
i
in
the search tree the following inequality holds:
∑
j
l=0
∑
k<l,c
kl
∈C
C(k,l) +
∑
l≥i
LB
l
≤ UB. Where LB
l
is the lower bound of the cost of agent A
l
for its con-
straints with the partial assignment in agent A
i
’s view.
A forward-consistent(FC) view is therefore also
BC. It guarantees that there exists an assignment, for
every agent ordered after agent A
i
, that is consistent
with this view’s partial assignment. Note that as-
signments of lower-priority agents are not included
in the view, and therefore may not be consistent with
each other. An agent that has a consistent view of
the search-process is guaranteed that the computation
triggered by its decisions will not be proven irrelevant
to finding a solution by a higher-priority agent.
Definition 5. Let agent A
i
be of lower-priority than
some agent A
j
. Let A
i
perform computation based on
an agent-view (or a cpa) containing A
j
. If there exists
an ordering of messages such that by the time the out-
come of A
i
’s computation reaches agent A
j
it already
holds a proof that the current view cannot be part of
an optimal solution, the computation performed by
agent A
i
is defined to be irrelevant.
A synchronous algorithm is one whereagents al-
ways hold consistent views of the search-process, and
thus do not perform irrelevant computations. Some
asynchronous algorithms, on the other hand, do not
keep any of the above properties and may potentially
perform irrelevant computations. However, asyn-
chronous algorithms are designed to perform com-
putations concurrently, attempting to lower the over-
all non-concurrent runtime. Asynchronous DCOP al-
gorithms can be shown to fall into one of the above
classes and, as a result, incorporate different potential
amounts of irrelevant computations.
SynchronizingforPerformance-DCOPAlgorithms
7

Let us go over several clear example algorithms
and their synchronization classes.
Synchronous Branch & Bound. In SyncBB (Hi-
rayama and Yokoo, 1997) each agent in a serial or-
der (e.g., in its turn) receives a CPA message, which
is a partial assignment that is a backwards-consistent
(BC) view of all (assigned) higher-priority agents.
The receiving agent tries to add its own assignment
to the CPA, verifies its backwards-consistency, and
passes it on. This naive algorithm doesn’t check
forward-consistency and as a result is outperformed
easily by algorithms that do. It is clear that the mecha-
nism of SyncBB is completely sequential. No compu-
tation can be proven irrelevant to the search-process.
Every consistency check either proves consistency of
all higher priority agents whose assignments are part
of the view that is the basis for the computation, or
removes a non empty part of the search process by
proving an inconsistency.
Synchronous Forward Bounding. SFB takes a more
eager approach, using a Forward-Bound mechanism.
Upon receiving a CPA message, the receiving agent
is guaranteed to have a forward-consistent (FC) view
of the search-process. Its procedure is to select an as-
signment (expand the cpa), verify consistency back-
wards, and send FB requests forward to receive FB
estimates (a lower bound LB
l
for each l > i ) that will
be summed up to a consistency-forward check against
the current value of the Upper-Bound. Following this
complete verification of forward-consistency, a CPA
message is sent to the next agent. If no consistent
value is found, the cpa has been proven (forward or
backward) inconsistent and therefore cannot be part
of any optimal solution. Clearly, the SFB algorithm
assures forward-consistent views, and therefore it be-
longs to a higher synchronization class than SyncBB.
Asynchronous Forward-Bounding. AFB (Gersh-
man et al., 2009) uses the same FB mechanism as
SFB with one difference. Similarly to SFB, once
an agent is done checking backwards-consistency on
its newly assigned value, it sends FB requests to
lower-priority agents requesting to verify forward-
consistency. However, it does not wait for approval
by all requested agents and the next agent is ex-
pected to immediately further expand the CPA and
send FB-requests of its own. This implies that an
agent A
i
receiving a CPA message is only guaranteed
backward-consistency of the view on the received
CPA. As a result, the receiving agent’s computations
may be proven irrelevant if a higher-priority agent
later revokes the received partial assignment. This
can happen if the higher priority agent (say, agent
A
j
, whose assignment appears on the CPA) has re-
ceived some FB estimate proving the view on the
CPA to be forward-inconsistent. Such a message will
cause a change of assignment of A
j
into an alternative
backward-consistent one (and the sending of a later-
time-stamped CPA message). This means that for this
specific case the agent that received the CPA might
have performed an irrelevant computation.
The run-time performance cost of an irrelevant
computation can vary, depending on the actual dis-
tributed computation taking place. It may be the case
that an agent performs irrelevant computation instead
of being idle, so that the non-concurrent run-time of
the algorithm is not necessarily lengthened. However,
two types of damage to the performance of the algo-
rithm can be incurred. First, the agent’s unavailability
to accept new messages while performing an irrele-
vant computation may delay the non-concurrent run-
time of the algorithm. Second, the communication
load of the system increases by the addition of (irrel-
evant) messages. A higher communication load may
cause deterioration in the delivery time of messages,
as well as create additional irrelevant computation.
3.1 Algorithms that use a DFS Tree
Some DCOP algorithms organize the agents into a
pseudo-tree (also known as a DFS tree) in order to
gain run-time performance by the resulting enhanced
concurrency (Modi et al., 2005; Yeoh et al., 2010;
Chechetka and Sycara, 2006). In a DFS tree, if
two agents share a constraint they are in an ancestor-
descendent relation. Any two agents which are not
in such a relation need not check consistency directly
with one another. This property enables the solving of
unrelated sub-problems concurrently. It also means
that the relation higher-priority than (lower-priority
than) is undefined for any two nodes that are not re-
lated as descendant-ancestor. As a result, the use of
a backward-consistent view by an agent does not suf-
fice for the same type of guarantee against irrelevant
computation as in the algorithms described above. At
any instant of the search process traversing the sub-
tree rooted at agent A
i
its parent may be informed by
another child of it (a sibling of agent A
i
) of a cost that
breaks its known Upper-Bound. The result of such
an event will be a re-assignment of the parent which
implies that the computation performed by all agents
within the subtree rooted at agent A
i
is irrelevant.
Non-commitment Branch and Bound. In NCBB
(Chechetka and Sycara, 2006) when agent A
i
receives
a search message from its parent, it has a view of the
SP that is backwards-consistent. A
i
then invokes mul-
tiple subtreeSearches (which are similar to request-
ing an FB-estimate) one per each child and value it
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
8

has. The invocations of subtree searches are done
iteratively, keeping every child occupied with some
calculation over a value still considered relevant. In
other words, for each non-busy child A
j
of Agent A
i
it selects a value (that was neither proven obsolete nor
explored by that child in the current search) and ini-
tializes a subtreeSearch
j
to get an FB-estimate of the
subtree rooted at A
j
. For each returned lower bound
(LB) estimate from a child’s subtree, A
i
replies with a
search message - pending that the sum of this value’s
back-costs and the cost estimates received so far are
still within bound, i.e. partially consistent-forward.
This utilizes concurrency among children, as each
subtree attempts to keep its children busy at all times,
not waiting for forward-bounds from all children be-
fore invoking a search, or before exploring other val-
ues on one subtree prior to them being fully explored
on another.
However, while one child returns an estimate or a
cost accumulating to a subtotal cost that is higher than
the known UB, other children may continue to explore
this (now obsolete) value. This has the potential effect
of delaying the search of other (relevant) values.
Branch-and-Bound ADOPT. In BnB-ADOPT
(Yeoh et al., 2010; W. Yeoh and Koenig, 2009;
Gutierrez et al., 2011) all agents start computation on
their current views (initially empty ones) and do not
wait for any message in order to start assigning val-
ues. Each agent sends a COST message to its parent,
and VALUE messages to its children and pseudo-
children (forward-edges). Every VALUE message
from an ancestor may cause a change of assignment
and further VALUE messages to descendants, and
every COST message from a child triggers a COST
message to the recipient’s parent. The result is that
VALUE messages are not backwards-consistent;
Consider an agent A
i
that receives a VALUE message
from one of its pseudo-parents agent A
j
which just
switched value. Agent A
i
may now hold a view with
assignments of agents on the path from A
j
to A
i
, that
were not checked for consistency against the VALUE
reported by A
j
. Furthermore, A
i
will now choose a
value and send its children and pseudo-children a
VALUE message carrying its view and its new as-
signment, none of which was checked for consistency
with all former assignments.
Asynchronous Distributed OPTimization. Alike
the former, ADOPT (Modi et al., 2005) agents start
computation on their current views (initially empty
ones) and do not wait for a sign in order to start as-
signing values. Agents send COST messages to their
parents, and VALUE messages to their children and
pseudo-children (forward-edges). Here too VALUE
messages are not backwards-consistent. However,
unlike BnB-ADOPT, this mechanism takes a unique
best-first approach, i.e. a change of assignment of
some agent A
i
is made whenever the currently ex-
plored value no longer has the best lower bound. This
means that an agent may change its assignment from
some value d
1
to a different one d
2
that currently has
a better lower bound, after the subtree of d
1
was only
partially explored. As a result, it may return to d
1
(and will need to reconstruct subtree cost) once d
2
is
explored some more. This may happen many times
during search, and effectively means that no assign-
ment can be ruled out until the very end of the search-
process, when the partial assignment becomes a full
assignment and is still considered as the “best” one.
The last step we take in differentiating levels of
synchronization requires the description of a weaker
synchronization element for the case of BnB-ADOPT
and we term it depth-first search. Searching in
a depth-first manner enables the synchronization of
pruning actions. When an agent receives a message
that reports the assignment of a higher-priority agent
that is different than its previous assignment, the re-
ceiving agent can be certain that the entire subspace
of solutions that is rooted at the sender’s former as-
signment is pruned from the search, never to be ex-
plored again. In other words, the receiving agent is in-
formed that any computation it performs that is based
on the former assignment(s) of the sender is neces-
sarily irrelevant. The property that we term depth-
first search differentiates the synchronization class of
ADOPT from that of BnB-ADOPT, which has this
property (as do protocols of a higher synchronization
class). The bottom line of the above categorization of
synchronization classes for DCOP algorithms is that
ADOPT is the least synchronized of all DCOP algo-
rithms. It does not belong even to the weakest class
(depth-first search) and agents computing against a re-
ceived partial assignment cannot be guaranteed that a
replaced assignment of some ancestor will not be vis-
ited again and may still be relevant.
Figure 1 is a scheme of DCOP algorithms by their
level of coordination. A Grade value of 1 describes
an algorithm that considers (views) a backward (re-
spectively, forward) expression of the compound as-
signment while expanding it. A grade 2 is given if the
assignment is BC (respectively, FC). Note that SBB
and SFB define the exact cases of BC and FC.
3.2 A Different Type of Concurrency
A different concept of concurrency is introduced
into DCOP search by the Concurrent Forward-
Bounding algorithm (Netzer et al., 2010). In Con-
SynchronizingforPerformance-DCOPAlgorithms
9

Backward view
Forward view
1
1
(considered)
2
2
(consistent)
Figure 1: Synchronization levels.
cFB, idle time is reduced by splitting the search-tree
into several disjoint subtrees, each explored by a dif-
ferent search-process(SP). The concept of a search
process was first introduced for distributed constraints
satisfaction in (Zivan and Meisels, 2006a) and in-
volves all of the agents. In order to improve effi-
ciency, each SP has a different agent hierarchy, ran-
domly or dynamically generated. When some SP
finds a complete solution (better than the last one),
all agents are informed of the new upper-bound (and
the best assignment known). This causes all other
SPs to consider a tighter UB, and prune faster partial-
assignments of higher cost. Each SP performs an
SFB search of its assigned subtree. As a result, each
SP guarantees that all CPA messages are forward-
consistent when sent and received. Consequently,
each computation against a received CPA message
is relevant. The only point in time where a compu-
tation can be irrelevant occurs when a new-solution
message, carrying a lower UB than the one known,
is on its way at the same time when an agent is busy
expanding some partial assignment, that is carrying a
cost higher than the new UB to arrive.
Any two concurrent SPs are independent of one
another, as they search disjoint parts of the global
search space. This is unlike an asynchronous mecha-
nism of a single search process, where multiple simul-
taneous computations may relate to the same search
space (cpa). Going back to the definitions of rele-
vance the proof that a specific ‘Conc’ search process
cannot lead to an optimal solution does not imply any-
thing about the optimality of any other SP.
4 IDLE TIME
Let us take a closer look at the behavior of the three
forward-bounding algorithms of the last section -
SFB; AFB; ConcFB. These are an excellent test case,
since the main difference between them is their level
of synchronization. A good starting point is to ex-
amine the bottleneck of SFB: idle-time imposed by
waits for approval of forward-consistency. Consider
some agent A
i
, presently holding the CPA with its par-
tial assignment CPA
0,...,i−1
and attempting an assign-
ment. A
i
’s first move is to choose some value, ver-
ify backwards-consistency, which will consume i con-
straint checks, and then send FB requests to all agents
A
j
( j > i) and await reply. The time (as measured
in constraint checks) needed for a receiving agent A
j
to handle an FB-request is: |dom| × (i + 1), because
A
j
has |dom| values to check, each against the i + 1
agents 0, 1,...,i assigned so far on the request’s CPA.
Thus, A
i
will wait |dom| × (i + 1) time for all replies.
This is the waiting time caused solely by computation
(message delivery times are accounted for later on).
Note that while agent A
i
holds the cpa, all agents
A
0
,...,A
i−1
are idle. For each agent A
k
(where k < i),
while A
i
holds the CPA, A
k
’s idle time amounts to the
number of tries for a value assignment performed by
agent A
i
times i for each try, and times |dom| ×(i+1)
which is A
i
’s waiting time for replies for each of its
value assignment tries:
Tries(i) × {AssignTime(i) + FBtime(i)} =
Tries(i) × {i + |dom| × (i + 1)}
(1)
Tries(i) is trivially bounded by |dom| × Tries(i −
1), where Tries(−1) = 1, but it is reduced both
as i increases, as well as with search progress, as
lower Upper-bounds are discovered and assignments
of higher cost are pruned earlier. Based on the above
considerations, the maximal total idle time during the
search due to computations can be formulated as:
n−1
∑
i=0
∑
j<i
Tries(i) × (i + |dom| × (i + 1)) +
∑
j>i
Tries(i) × i
!
(2)
Note that the inner sums are for j, but they are
independent of it. It simply reflects the fact that ev-
ery agent is idle during the computation performed by
agent A
i
. The above computation of idle time is not
a non-concurrent time. On the contrary, it can add up
to n − 1 times the non-concurrent time (in SyncBB, a
sum of this sort is exactly n − 1 times the number of
NCCCs). It reflects the total time wasted by n system
nodes as they were pending for messages. This idle
time needs to be utilized by the system and its mini-
mization is a main goal of any concurrent algorithm.
The method of saving idle time employed by the
AFB algorithm (and all other asynchronous branch
& bound algorithms) saves FBtime(i) on the one
hand, but sometimes significantly increases Tries(i)
on the other. This happens because less values are
pruned by enforcing backwards-consistency (neglect-
ing forward-consistency enforcement). AFB’s in-
crease of Tries(i) (compared to SFB) triggers a rip-
ple effect: it increases Tries(i + 1), since agent A
i+1
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
10

sends an FB-estimate to A
i
and expands the CPA and
sends FB-requests of its own. This ripple continues
until a new FB-request message from A
i
arrives at the
top of the inbox of A
j
( j > i), when a new ripple is
created. This does not only happen at the expense of
idle time. When some agent A
j
is occupied with a
calculation on an irrelevant CPA, a newer CPA to ex-
plore (or estimate upon) can be waiting in its inbox,
causing an increase of the sender’s idle time.
The above analysis of idle time assumes that mes-
sages arrive instantanously, counting only computa-
tion time. In real-life distributed systems, where
communication is transferred by a computer network,
messages take a finite time to arrive at their destina-
tion. It turns out that once messages take time to be
delivered, a more realistic analysis of the impact of
synchronization class on non-concurrent run-time of
DCOP algorithms can be performed.
4.1 Adding Message Delivery Times
Assume that message delivery consumes a random
time, uniformly distributed in the range of [0, ..., m],
time units. This may happen when network messages
are sent by servers that respond differently to geo-
graphical distances between nodes. A uniform distri-
bution model for such delays is compatible with some
basic assumed symmetry.
Since message transfer time is not a constant, mes-
sages do not arrive all at once. This may cause (in
AFB’s case) some agents to receive an irrelevant FB-
request, while others will eliminate it—receiving a
newer FB attempt from a higher-priority agent first.
SFB’s synchronous behavior dictates a wait
for all agents to reply with an FB-response before
making a decision. This means that the time spent
from the moment agent A
i
sends an FB-request and
until all responses accumulate back is expected to
be max
j>i
{m
i→ j
+ m
j→i
} where m
k→l
v U[0..m].
The distribution function of the time needed for
an FB-request and reply to arrive at lower-priority
agents is therefore:
F
(n−i)
(t) =
t
2
2m
2
n−i
,0 ≤ t ≤ m
t(4m−t)
2m
2
− 1
n−i
,m ≤ t ≤ 2m
A graphical description of such a function is pre-
sented in figure 2. As i grows (less neighbors are
ahead), the graph curves up for lower values of t,
i.e. as there are less neighbors to send to (and re-
ceive from) messages, it is more likely that the maxi-
mal time for send and receive will be shorter. For the
extreme case where i = n − 1, where there is only one
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2
time as a coefficient of m
Pr(max{m_i->j +m_j->i} < t) per agents ahead
1
2
3
4
5
6
7
8
Figure 2: Distribution function of time for FB request and
reply.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29
E(time)=m*__
Amount of forward-binders
Figure 3: Expected time of FB-request-and-reply per
amount of agents ahead.
neighbor ahead, Pr(send + receive ≤ m) = 0.5, and
the curve is simply wider.
In SFB’s case, when some agent A
i
sends an FB-
request, it is expected to wait E(max{m
i→ j
+ m
j→i
}),
which once again depends on the amount of agents
ahead, as described in figure 3.
Upon success of an assignment, where FB-
responses will prove the CPA to be forward-
consistent, AFB is expected to save the time needed
for all response-messages to arrive and the ap-
proval message from A
i
to A
i+1
, which amounts to:
E(max
j>i
m
j→i
+ m
i→i+1
). Although this formula is
dependent upon the amount of agents ahead, its out-
come is in [m..3m/2]. The relation between maxi-
mal message delivery time m and computation time,
denoted by c, is imperative to the comparison. If
c << m, then upon success AFB saves up to 3m/2
compared to SFB which waits for all responses. Upon
failure of Forward-bounding, in this scenario, AFB
does not waste any time, since any irrelevant message
arriving before the next FB-request from A
i
arrives
while the analogous SFB agent is idle. When the new
FB-request from i arrives, it may have to wait to be
processed as much as: ( j − i) · c time units (based
on the maximal amount of irrelevant FB-requests that
may arrive before it). If c is small enough compared
to m, AFB has not lost any significant time.
In the other extreme c >> m. Upon success, AFB
saves an insignificant amount of time (m), where fail-
ure in forward-bounding an assignment of some A
i
generates a ripple of irrelevant messages from A
i+1
which are expected to arrive to other agents A
j
, j >
i + 1 just before the new FB-request A
i
is about to
send. This causes a delay of roughly c time units.
When c ≈ m, if forward-bounding succeeds, AFB
SynchronizingforPerformance-DCOPAlgorithms
11

is expected to save up to m time units (pending, as
above, on the amount of agents ahead), as SFB has
to wait for FB responses (maximal message time) be-
fore passing on the CPA. Note that the time c added to
SFB is not insignificant, but A
i+1
consumes the same
time in AFB as it expands the CPA (and responds to
the FB-request). Upon failure of forward-bounding,
there is a significant cost to AFB’s run time. This is
because some agent A
j
, ( j > i + 1) may be occupied
with irrelevant computation caused by messages from
all agents A
i+1
,A
i+2
,...,A
j−1
at the time the next mes-
sage from A
i
arrives. The actual amount of delay dif-
fers according to the precise relation between c and m
and the amount of agents ahead, but by examining for
instance, the delay imposed by A
i+3
as it may receive
irrelevant messages from A
i+1
as well as from A
i+2
causing it to become unavailable to process the next
(relevant) FB-request from A
i
as it arrives, it is clear
that the search process could be delayed by up to 2c
time units. Under the assumption that c is roughly
m/2 (the expected message time), the expected delay
imposed by A
i+3
for each failure is slightly over m/7
( 0.14731 · m)
2
. Thus, for a success/failure ratio of
1 : 7 or worse, SFB runs faster.
4.2 Comparing to ConcFB
Let us turn now to the method of decreasing idle time
that is employed by the third algorithm - ConcFB.
In ConcFB, the search space is divided into several
disjoint sub-spaces, each explored by an independent
Synchronous Search-Process. Each SP has a random
or dynamically created order of agents, so while some
agent awaits a reply or a CPA in one SP, it is kept
busy computing for other SPs. This calls for some
more memory, to keep track of each SP, but idle time
is reduced, and there is less irrelevant computation.
The only time where a computation may be irrele-
vant is when a New Solution message is in the in-
box queue of some agent A
i
, carrying an UB so low
that it is about to prune the CPA that A
i
is currently
computing upon. New Solution messages are a lot
rarer than both FB-requests and CPA messages. Em-
pirically, problems with 12 agents, and 6 domain val-
ues each, have about 10 New Solution messages dur-
ing the entire search. The total amount of messages
during the same concFB search is roughly 200,000.
Consequently, this type of concurrency does not cre-
ate massive irrelevant computation, and since it also
evenly spreads the computation load (and order), it is
2
Based on a complex probabilistic aggregation of prob-
abilities for delay times the delays imposed in each possible
message arrival time and order for m = 10, (n − i) = 10 and
c = 5.
less susceptible to the impact of message delays.
For better intuition, consider ConcFB’s time uti-
lization potential: As each SP is an SFB-like protocol,
at any given time, a search-process may be (1)at some
agent, expanding the cpa or (2)calculating FB esti-
mates. A third option exists, where the SP awaits at-
tendance in an occupied agent’s inbox, which is why
the mechanism must balance the amount of concur-
rent SPs, but this is also not directly relevant to the
current analysis, that focuses on minimizing idle-time
- keeping agents busy at one hand, and not increas-
ing the amount of computation needed on the other.
While an SP is in the assign phase (1) a single agent
is computing thus only 1/n of the agents are active
and the rest are idle (ignoring the existence of other
SPs for the moment). While an SP is on an FB phase,
taking the average case of FB estimate for a median
agent A
i
(i = n/2), a fraction α of unassigned agents
are neighbors of A
i
and thus α/(0.5·n) agents are ac-
tive at that time, and the rest are idle. Had we known
the relation between time consumptions of (1) and (2)
we could calculate the expected amount of idle agents
at a random time, and moreover calculate the amount
of concurrent SPs needed to maximize agent activ-
ity levels at all times (recall that agents are dynami-
cally ordered, thus the load is expected to be evenly
distributed). Increased system delay times obviously
lowers the system’s activity level, and therefore calls
for some more concurrent SPs to compensate.
5 EXPERIMENTAL EVALUATION
The first set of experiments, depicted in Figures 4
and 5, shows a categorical partition of algorithms into
synchronization classes and the clear correlation be-
tween synchronization level and performance, mea-
sured by non-concurrent constraint-checks(Meisels
et al., 2002) and network load. This experiment was
run over problems with 10 agents and 6 domain values
per agent. p
1
marks the probability for two agents to
share a constraint, and constraint costs are randomly
distributed in [0, 1, ..., 100]. For each p
1
value, 100
random problems have been generated and averaged.
To correlate between the class of synchro-
nization and performance level, recall that BnB-
Adopt(Gutierrez and Meseguer, 2010) was catego-
rized as a depth-first class, which is stronger than
ADOPT’s class. ADOPT could not complete the
search in this size of problems under our simula-
tion limits. Higher than BnB-Adopt in synchroniza-
tion level are backwards-consistent algorithms such
as SyncBB, which is shown to perform better as prob-
lems become more dense. The other three algorithms
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
12
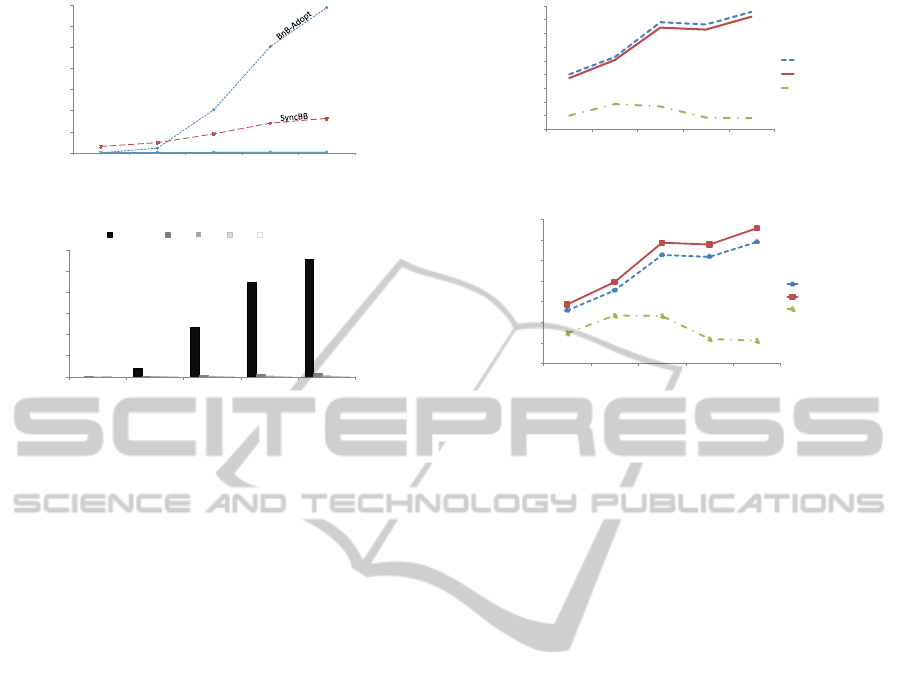
0
100
200
300
400
500
600
700
0.1 0.3 0.5 0.7 0.9
NCCCs (Millions)
P1
AFB, SFB, ConcFB
Figure 4: Runtime in NCCCs - synchronization classes.
0
1
2
3
4
5
6
0.1 0.3 0.5 0.7 0.9
Messages (Millions)
P1
BnB-Adopt SBB AFB SFB ConcFB
Figure 5: Total message count.
(AFB, SFB, ConcFB) seem to perform similarly. This
is due to the scale of the graphs in Figures 4 and
5. The relations between these three are clearer when
compared separately, as in the following experiments.
The next group of experiments demonstrates the
differences between SFB, AFB and ConcFB as ana-
lyzed in Section 4. It shows that under different net-
work conditions, AFB and SFB may outperform one
another, depending on the ratio between computation
time c and message delivery time m. It also shows that
a synchronized multiple-SP mechanism outperforms
them both under all network conditions. These ex-
periments were run on the same batches of problems,
each problem has 12 agents and 6 domain values per
agent, with p
1
values of 0.3,0.4,0.5,0.6,0.7. For ev-
ery p
1
value 50 random problems were averaged.
According to the description of Section 4, SFB is a
forward-consistent search-process whose main draw-
back is idle-time. The mechanisms of the other two
algorithms - AFB and ConcFB - offer to eliminate this
drawback to achieve a faster search-algorithm.
Figure 6 shows the results of an experiment where
messages arrive instantly, and “time” is measured in
NCCCs. This simulation corresponds to the case
where computation time is much longer than com-
munication time. As estimated in Section 4, when
c >> m AFB’s irrelevant computation does not hap-
pen only at the expense of idle-time. Agents may
become unavailable to respond to relevant messages
and lengthen the algorithm’s runtime. ConcFB, on
the other hand, has no irrelevant computation and its
method of splitting the search-space into separate sub-
spaces and searching those simultaneously turns out
to perform much better.
0
3
6
9
12
15
18
21
24
27
0.3 0.4 0.5 0.6 0.7
NCCCs (millions)
AFB
SFB
ConcFB
Figure 6: Synchronous vs. Asynchronous vs. concurrent -
c >> m.
0
10
20
30
40
50
60
70
0.3 0.4 0.5 0.6 0.7
NCCCs (Millions)
AFB
SFB
ConcFB
Figure 7: Synchronous vs. Asynchronous vs. concurrent -
c ≈ m.
Figure 7 depicts the results of running the same
problems of Figure 6 in a system where message de-
livery time is not zero (simulation is based on (Zi-
van and Meisels, 2006b; Zivan and Meisels, 2006c)).
Each message is delayed randomly in the range of
[0,1,...,100], where time is measured in NCCCs.
This gives an expected delay of 50 time units per
message, and is comparable to the average number
of constraint-checks an agent performs per message
(as sampled empirically). Similar experiments with
normally distributed delays shows same relations, and
were not brought here for lack of space
Message delay times accumulate in the NCCCs
clock, and hence the total time measures increase dra-
matically. AFB is slightly faster than SFB in such a
system. Not waiting for forward-bound was benefi-
cial and had saved more time than the time consumed
by irrelevant computation. In contrast, the runtime of
the ConcFB algorithm stays better than the other two
algorithms (as in the case of instantaneous masseges).
The last experiment focuses on very large message
delays, so that message delivery takes a lot longer
than computation time, i.e. c << m. Random de-
lays were in the range of [0, 1, ..., 1000] per message
which accumulates to a Non-Concurrent Steps Count
(NCSC) clock(Meisels et al., 2002). This clock actu-
ally measures the longest path in messages throughout
the algorithm’s run. Since computation time is irrele-
vant in the current scenario, it is a natural clock.
The graph demonstrates the claim of Section 4. In
a system where messages have high cost, AFB per-
forms better than SFB since irrelevant computation is
done at the expense of idle-time. ConcFB shows re-
sistance to very long delays. Instead of risking irrele-
vant computation, each SP explores a different part of
SynchronizingforPerformance-DCOPAlgorithms
13

0
50
100
150
200
250
300
350
400
450
0.3 0.4 0.5 0.6 0.7
NCSC (Millions)
AFB
SFB
ConcFB
Figure 8: Synchronous vs. Asynchronous vs. concurrent,
c << m.
0
100
200
300
400
500
600
0.3 0.4 0.5 0.6 0.7
Messages (Thousands)
AFB SFB ConcFB
Figure 9: Synchronous vs. Asynchronous vs. concurrent -
average network load by problem density.
0
200
400
600
800
1000
1200
0 1 2 3 4 5 6 7 8 9 10 11
Messages (Thousands)
AFB SFB ConcFB
Figure 10: Synchronous vs. Asynchronous vs. concurrent -
average network load by agent.
the search tree, and whenever a high-quality solution
is found, all other SPs can be pruned faster.
Regarding the network’s communication load,
Figures 9 and 10 illustrate the typical load-ratio be-
tween the three algorithms. Considering the system’s
overall communication load as presented in Figure 9
both AFB and ConcFB exchange more messages
than SFB. However, as shown in Figure 10, ConcFB
spreads the load evenly between all agents (besides
the first agent that merely initiates the search).
6 CONCLUSIONS
A classification of DCOP search protocols into
classes of synchronization has been presented. The
analysis of non-concurrent run-time of DCOP algo-
rithms identifies a drawback of synchronization in the
form of idle time and the trade-off with irrelevant
computation that are the result of asynchronous algo-
rithms attempting to decrease agents’ idle time. The
solution was given by the Conc mechanism. It uses
several distinct search processes concurrently, each
responsible for a different part of the search space.
When the concurrent mechanism is applied to syn-
chronous search-processes, irrelevant computations
are avoided, as well as an overload of the network
with redundant messages.
REFERENCES
Bessiere, C., Maestre, A., Brito, I., and Meseguer, P. (2005).
Asynchronous Backtracking without adding links: a
new member in the ABT Family. Artificial Intelli-
gence, 161:1-2:7–24.
Chechetka, A. and Sycara, K. (2006). An any-space algo-
rithm for distributed constraint optimization. In Proc.
AAAI Spring Symp. Distr. Plan Sched. Manag.
Gershman, A., Meisels, A., and Zivan, R. (2009). Asyn-
chronous Forward Bounding for Distributed COPs. J.
Artif. Intell. Res. (JAIR), 34:61–88.
Gutierrez, P. and Meseguer, P. (2010). Saving redundant
messages in bnb-adopt. In Proc. 24th AAAI Conf. Ar-
tif. Intell. (AAAI-10), pages 1259–1260.
Gutierrez, P., Meseguer, P., and Yeoh, W. (2011). General-
izing adopt and bnb-adopt. In Proc. 23rd Intern. Joint
Conf. Artif. Intell. (IJCAI-11), pages 554–559.
Hirayama, K. and Yokoo, M. (1997). Distributed partial
constraint satisfaction problem. In Proc. CP-97, pages
222–236.
Meisels, A. (2008). Distributed search by constrained
agents. Springer Verlag.
Meisels, A., Razgon, I., Kaplansky, E., and Zivan, R.
(2002). Comparing performance of distributed con-
straints processing algorithms. In Proc. AAMAS-2002
Workshop on Distributed Constraint Reasoning DCR,
pages 86–93, Bologna.
Modi, P. J., Shen, W., Tambe, M., and Yokoo, M. (2005).
Adopt: asynchronous distributed constraints opti-
mization with quality guarantees. Artificial Intelli-
gence, 161:1-2:149–180.
Netzer, A., Meisels, A., and Grubshtein, A. (2010). Concur-
rent Forward Bounding for DCOPs. In Proc. 12th in-
tern. workshop Dist. Const. Reas. (DCR-10) (AAMAS-
10), Toronto.
W. Yeoh, X. S. and Koenig, S. (2009). Trading off solu-
tion quality for faster computation in dcop search al-
gorithms. In Proc. 21st Intern. Joint Conf. Artif. Intell.
(IJCAI-09), pages 354–360.
Yeoh, W., Felner, A., and Koenig, S. (2010). Bnb-adopt:
An asynchronous branch-and-bound dcop algorithm.
J. Artif. Intell. Res. (JAIR), 38:85–133.
Yokoo, M. (2000). Algorithms for distributed constraint sat-
isfaction problems: A review. Autonomous Agents &
Multi-Agent Sys., 3:198–212.
Zivan, R. and Meisels, A. (2006a). Concurrent search for
distributed csps. Artif. Intell., 170(4-5):440–461.
Zivan, R. and Meisels, A. (2006b). Message delay and asyn-
chronous discsp search. Archives of Control Sciences,
16(2):221–242.
Zivan, R. and Meisels, A. (2006c). Message delay and
discsp search algorithms. Ann. Math. Artif. Intell.
(AMAI), 46:415–439.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
14
