
Detection of Symmetry Points in Images
Christoph Dalitz, Regina Pohle-Fr
¨
ohlich and Tobias Bolten
Institute for Pattern Recognition, Niederrhein University of Applied Sciences, Reinarzstr. 49, Krefeld, Germany
Keywords:
Symmetry Detection, Symmetry Transform.
Abstract:
This article proposes a new method for detecting symmetry points in images. Like other symmetry detection
algorithms, it assigns a “symmetry score” to each image point. Our symmetry measure is only based on scalar
products between gradients and is therefore both easy to implement and of low runtime complexity. Moreover,
our approach also yields the size of the symmetry region without additional computational effort. As both axial
symmetries as well as some rotational symmetries can result in a point symmetry, we propose and evaluate
different methods for identifying the rotational symmetries. We evaluate our method on two different test sets
of real world images and compare it to several other rotational symmetry detection methods.
1 INTRODUCTION
Symmetry can be a useful feature for the identifica-
tion both of natural objects, like faces (Tao et al.,
2009), as well as man-made objects, like vehicles
(Kuehnle, 1991). Consequently, algorithms for de-
tecting symmetry points in images have been an area
of research for some time (Reisfeld et al., 1995) (Loy
and Zelinsky, 2003) (Loy and Eklundh, 2006) (Lee
and Liu, 2010). For a survey of symmetry detection
algorithms, see (Liu et al., 2009). All of these algo-
rithms assign each image point a “symmetry score”
that measures how well the point works as the origin
of a mirror operation. The image of symmetry score
values can then be considered as a “symmetry trans-
form” of the original image, and symmetry points cor-
respond to maxima in the symmetry transform image.
The symmetry score computation depends on the
type of symmetry. The method by Kuehnle (Kuehnle,
1991), e.g., specifically looks for vertical symmetry
axes, Reisfeld et al. (Reisfeld et al., 1995) as well as
Loy & Eklundh (Loy and Eklundh, 2006) propose dif-
ferent methods for point reflection or rotation symme-
try, while Loy & Zelinsky (Loy and Zelinsky, 2003)
and Lee & Liu (Lee and Liu, 2010) consider rotational
symmetry. The method proposed in the present paper
is designed for point reflection symmetry, which is the
same as a rotation by π around the mirror point. Let
C
n
denote the symmetry group of a rotation by an an-
gle 2π/n. Then we are looking for symmetry points of
objects with a symmetry group C
2m
, because, when an
object is invariant under a rotation by π/m, it is also
invariant under a rotation by π.
A problem in symmetry detection is that the size
of the symmetric object is generally not known be-
forehand. For computing the symmetry score value
however, ideally only pixels belonging to the object
should be considered. The symmetry transform by
Reisfeld et al. (Reisfeld et al., 1995) requires an in-
put parameter that suppresses distant pixels exponen-
tially, which sidesteps the problem by letting the user
guess an object radius. The method by Lee & Liu
(Lee and Liu, 2010) tries a whole range of radii, but
this adds even more computational complexity to an
already very complex method. As a workaround, they
suggest the use of image pyramids so that only re-
gions that seem promising in low resolutions are ex-
amined in full detail. Our method in the present paper
offers a different solution via a recursion formula that
connects the score value for radius r +1 with the score
value for radius r, which reduces the computational
overhead of trying different radii considerably.
Another problem for the detection of rotational
symmetric objects is that, depending on the view
point, the symmetry can be “skewed” (Kanade, 1981)
(see Fig. 1(a)). Lee & Liu address this problem with a
frieze expansion around each potential rotation center
(Lee and Liu, 2010). A simpler approach with con-
siderably less computational cost can be based on the
observation that a C
2m
symmetry approximately be-
comes a point reflection (C
2
) symmetry, provided the
object does not extend too much in the direction per-
pendicular to the image plane. In practice, rotational
symmetry will therefore generally show up as a C
2
symmetry, for which our method is specifically de-
signed.
577
Dalitz C., Pohle-Fröhlich R. and Bolten T..
Detection of Symmetry Points in Images.
DOI: 10.5220/0004179405770585
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 577-585
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

(a) A C
4
rotational symmetry no longer holds
under distortion of perspective.
π
axis
rotation by
symmetry
(b) A C
2
rotational symmetry that also has an axial
symmetry.
Figure 1: The problems of “skewed symmetry” and axial
symmetry in rotational symmetry detection.
It should be noted however, that some pure axial
symmetries also show up as C
2
symmetries. A partic-
ularly frequent case are parallel lines (see Fig. 1(b)).
When detecting rotational symmetry through point re-
flection symmetries, it is thus necessary to distinguish
the actual rotation symmetries from pure axial sym-
metries. In this paper we will investigate different cri-
teria for making this discrimination.
This paper is organized as follows: Sec. 2 de-
scribes the computation of our symmetry score value
and the determination of the symmetry radius. Sec. 3
describes different possible features useful for distin-
guishing high score points belonging to a rotational
symmetry from those belonging to an axial symme-
try. Sec. 4 evaluates these features on a dataset of
real world images. Moreover, the resulting symme-
try detection is compared on two different data sets to
the classic method by Reisfeld et al. (Reisfeld et al.,
1995) (Reisfeld et al., 1990) and to the newer method
by Loy & Eklundh (Loy and Eklundh, 2006), which
was reported as the best method in (Park et al., 2008)
and (Rauschert et al., 2011). In the final Sec. 5, we
discuss open questions and make suggestions for fur-
ther research.
The source code of our symmetry transform and
the test data set with ground truth information will be
made available on the authors’ website
1
.
2 THE SYMMETRY DETECTION
METHOD
The general approach to symmetry detection consists
in first computing a measure for the symmetry of each
1
http://informatik.hsnr.de/∼dalitz/data/visapp13/
(x − dx, y − dy)
(x + dx, y + dy)
(x, y)
G
= −
GG’
→
→→
Figure 2: Point reflection of an image at point (x,y) maps
the gradient
~
G at (x + dx,y + dy) onto the gradient
~
G
0
at
(x − dx,y − dy).
point, and then selecting points with a high symmetry
score. In this section, we define a measure for point
symmetry and show how this measure cannot only be
utilized for detecting symmetry points, but also the
size of the symmetry region.
2.1 The Symmetry Measure
Like Reisfeld et al. (Reisfeld et al., 1995), we uti-
lize the gradient image rather than the original image,
because we do not want homogeneous regions to be
recognized as symmetric. The gradient image can be
computed from a greyscale image with a Sobel filter
(Gonzalez and Woods, 2002). Let us denote the gra-
dient image with
~
G(x,y). When an image is mirrored
at point (x,y), the gradient
~
G(x +dx, y +dy) becomes
−
~
G(x −dx,y −dy) (see Fig. 2). We conclude that one
necessary condition for symmetry around point (x,y)
is that these two gradients point in opposite directions,
or that their scalar product h·,·i is negative:
D
~
G(x + dx,y + dy),
~
G(x − dx,y − dy)
E
< 0 (1)
This scalar product takes a minimum when the two
gradients are anti parallel. We therefore define as a
measure for the symmetry around point (x,y)
S(x,y, r) = −
r
∑
dy=1
r
∑
dx=−r
.. .
D
~
G(x + dx,y + dy),
~
G(x − dx,y − dy)
E
−
r
∑
dx=1
D
~
G(x + dx,y),
~
G(x − dx,y)
E
(2)
where r is the radius of the symmetry region. The
sum omits the negative values dy < 0 because these
are already taken into account by the mirror operation
in the argument of the gradient. The symmetry point
(x,y) itself is completely omitted in the sum. The mi-
nus sign is added for convenience so that S is larger
for higher symmetry, not vice versa.
It should be noted that the measure (2) does not
only take into account the gradient directions, but also
their absolute strength. This has the effect that sym-
metric regions with strong edges have a higher sym-
metry measure than regions with weaker edges, but
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
578

otherwise the same symmetry. One way to smooth
out this difference is by transforming the gradient
strength as suggested by Reisfeld et al. (Reisfeld
et al., 1995):
~
H =
~
G
k
~
Gk
· log(1 + k
~
Gk) (3)
and then applying (2) to
~
H instead of
~
G. Instead
of log(1 + x), any other monotonous transformation
could be used, of course. It is an open question how-
ever, whether such a rescaling actually improves the
detection of symmetry points. The experiments de-
scribed in Sec. 4 have therefore been done both with
transformed and untransformed gradients.
2.2 The Size of the Symmetry Region
When the symmetry measure S(x,y,r) according to
(2) is evaluated for different values of r, this pro-
vides a way to automatically determine the size of
the symmetry region around (x,y). Unlike the sym-
metry measure by Reisfeld et al., (2) does not in-
clude an exponential damping factor depending on a
predefined region size. This means that, for a given
point (x,y), the values S(x,y,r) can be subsequently
computed for r = 1, 2,...,r
max
without any additional
computational effort, simply by reordering the sum
(2) to
S(x,y, r) = S(x,y, r − 1)
−
r
∑
dx=−r
D
~
G(x + dx,y + r),
~
G(x − dx,y − r)
E
−
r−1
∑
dy=−r+1
D
~
G(x + r,y + dy),
~
G(x − r,y − dy)
E
(4)
The symmetry value S(x,y) and region radius R(x,y)
for a point (x,y) can then be defined as
R(x,y) = argmax{S(x,y, r) |r = 1,. .. ,r
max
}
and S(x,y) = S(x,y,R) (5)
When the region radius is close to r
max
, larger values
for r could also be tried to find the next local max-
imum of S. This can save some computing time be-
cause large radii are then only investigated at “promis-
ing” points.
2.3 Runtime Complexity
For an image with n pixels, the Sobel filter requires
9n additions and n multiplications and is thus an O(n)
algorithm. The symmetry transform requires r
2
max
/2
multiplications and additions for each pixel. As both
operations are done subsequently, the total runtime of
our symmetry transform is O(r
2
max
· n). Even though
this is in O-Notation the same runtime complexity as
for the symmetry transform by Reisfeld et al., our
transform is considerably faster, because it only re-
quires algebraic operations and no exponential and
trigonometric functions. Loy & Eklundh did not es-
timate the runtime complexity of their algorithm in
(Loy and Eklundh, 2006). As their algorithm does
not take all image pixels as input, but only the much
smaller set of SIFT feature points (Lowe, 2004), the
runtime complexity depends on two factors: the run-
time complexity of the SIFT extraction, and the num-
ber of SIFT points returned, which depend very much
on the image content, thereby making a worst case
runtime estimation difficult.
On an Intel P8400 2.26 GHz CPU and with r
max
=
50, our algorithm took constantly 0.2 sec on a 200 ×
150 image from the CVPR 2011 dataset and 2.7 sec
on a 600 × 400 image from our dataset, while an op-
timized implementation (exponentials replaced with
lookup tables) of Reisfeld’s transform took about 9
sec (200 × 150, σ = 25) and 250 sec (600 × 400,
σ = 25), respectively. The runtime of Loy & Ek-
lundh’s algorithm varied considerably over the im-
ages and was between 0.3 and 1.0 sec on a 200 × 150
image, and between 1 and 18 sec on a 600 × 400 im-
age.
3 ROTATIONAL VERSUS AXIAL
SYMMETRY
As can be seen in Fig. 3, the symmetry transform de-
scribed in Sec. 2 assigns high score values to centers
of point symmetry. Some of these belong to rotational
symmetries, while others belong to axial symmetries,
mostly due to parallel strong edge lines. To discrim-
inate between these types of symmetry, we observe
that, for an axial symmetry, we obtain other sym-
metry points when moving from one symmetry point
along the symmetry axis. The same does not hold
for a purely rotational symmetry. This means that ax-
ial symmetries result in line shaped regions of high
symmetry scores, while rotational symmetries lead to
more circularly shaped regions of high symmetry. We
have therefore implemented the following three fea-
tures for determining the symmetry type of a given
candidate point (x,y):
Edge Directedness, computed on the gradient of
the symmetry transform. This measures how
“strongly directed” the edges of the symmetry
transform are. The feature is the maximum rel-
ative frequency in a histogram of the edge direc-
tions, weighted by the gradient absolute value,
DetectionofSymmetryPointsinImages
579

Figure 3: Symmetry transform according to Eqs. (4) and (5) of the image on the left.
in a k × k window around point (x,y). Natural
choices for the number of bins in the direction
histogram are 8 or 16. The “edge directedness”
should be higher for axial symmetries.
Covariance Eigenratio, computed on the symmetry
transform image. We compute the covariance ma-
trix K for the points in a k × k window around
(x,y) as
K =
1
N
k/2
∑
dx=−k/2
k/2
∑
dy=−k/2
S(x + dx,y + dy)
×
dxdx dxdy
dydx dydy
(6)
where S(x,y) is the symmetry transform value at
(x,y), and the normalization factor N is the sum
over all symmetry values in the window. The
eigenvalues of K indicate how strongly the val-
ues spread in the direction of the corresponding
eigenvector. Consequently, the ratio between the
smaller and the larger eigenvalue should be higher
for rotational symmetry, which are more isotropi-
cally spread around (x,y).
Antiparallel Directions, computed on the gradient
of the original greyscale image. We compute
the direction histogram of all gradients in a win-
dow with the symmetry radius R(x,y) according
to Eq. (5). Only those gradients are taken into
account for which the mirrored gradient is “an-
tiparallel”, i.e. the cosine of the angles between
the gradients is less than -0.975. The feature is
the highest relative frequency in the direction his-
togram. Again the number of histogram bins can
be 8 or 16. The value for “antiparallel directions”
should be lower for rotational symmetries.
In our experiments, described in Sec. 4.1, the feature
edge directedness with 16 histogram bins showed the
best performance.
4 EXPERIMENTAL RESULTS
For testing symmetry detection, there are currently
not many data sets available. Park et al. (Park et al.,
2008) selected images from different object recogni-
tion datasets for the CVPR 2008 conference, but the
resulting dataset is no longer available. At the CVPR
2011 conference, there was a workshop on symme-
try detection, and the data set, consisting of 42 im-
ages, used for evaluation is still available (Rauschert
et al., 2011). As using this data set allowed us to com-
pare our method to the other methods evaluated in this
workshop, we have used this as one of our test sets.
To allow for a more detailed investigation both of
our method and for future research, we have addi-
tionally created a new larger test set and ground truth
data. The new data set consists of 159 images of size
600×400, containing 27 different subjects. Each sub-
ject is shown in different perspectives and both in con-
text and in detail. The detail images can be useful
because, in the contextual images, the environment
often shows additional incidental symmetries. Like
Park et al. (Park et al., 2008), we have only labelled
those C
2m
symmetries that are “visually obvious dom-
inant symmetries” according to human observers. In
the ground truth meta data, we have labelled the sym-
metry points and the radius of the symmetric region.
We have used these images both for an evaluation
of the rotational symmetry detection, and for an eval-
uation of the symmetry type discrimination. For the
latter we have created different ground truth data and
a different set of test points.
4.1 Evaluation of Symmetry Type
Discrimination
To evaluate the three features described in Sec. 3 for
discriminating between rotational and axial symmetry
points, we have selected the ten highest local maxima
in the symmetry transform of each image from our
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
580
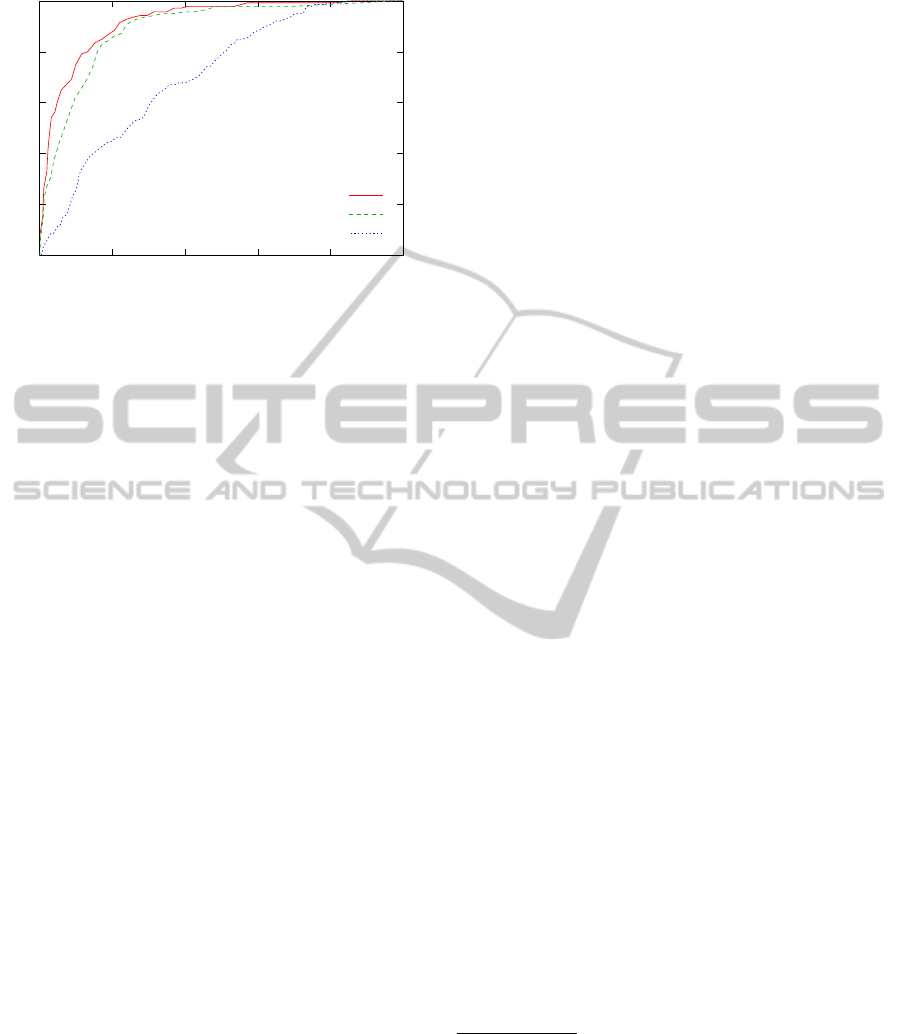
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
false rotational symmetries
edge directedness
antiparallel directions
covariance eigenratio
true rotational symmetries
Figure 4: ROC curve comparing the performance of the
three features for discriminating between rotational and ax-
ial symmetry. “False rotational symmetries” denotes the
rate of the axial symmetries erroneously classified as rota-
tional symmetries, and “true rotational symmetries” the rate
of the correctly classified rotational symmetries.
own test set, and labeled these points manually as be-
longing to an axial or rotational symmetry. After an
omission of unclear cases, these provided a test set
of 1346 symmetry points, of which 140 belonged to
rotational symmetry.
For each feature, the classification is based on a
threshold on the feature value. By comparing the rates
of correctly and erroneously detected rotational sym-
metries for different thresholds, we can thus compare
the discriminating power of the three features. For the
k × k windows, we have used k = 7, and as numbers
of histogram bins we have tested 8 and 16. In the case
of “edge directedness”, 16 bins were better, and for
“antiparallel directions”, 8 bins were better, i.e. had
a higher area under the ROC curve (AUC). The ROC
curves in Fig. 4 show that “edge directedness” per-
formed best on our test data. Even though the feature
“antiparallel directions” has a clearly larger AUC than
“covariance eigenratio”, it is still slightly lower than
that of “edge directedness”. As “edge directedness”
has the additional advantage of being faster to com-
pute due to the smaller window size, we have used
this feature for sorting out the axial symmetries. The
values in the upper left corner of the ROC curve cor-
respond to thresholds between 0.23 and 0.29 for the
“edge directedness”, so that we have chosen a thresh-
old of 0.27 as the criterion for rotational/axial sym-
metry discrimination in Sec. 4.2.
4.2 Evaluation of Rotational Symmetry
Detection
To compare a new method with other methods for ro-
tational symmetry detection, there are principally two
approaches: one is to implement and run the different
algorithms on a new test set, the other one is to run the
new algorithm on an older data set for which results
have already been reported in an earlier study. For the
latter approach, we have used the CVPR 2011 data
set (Rauschert et al., 2011). For the former approach,
we have deployed the code published by Loy & Ek-
lundh on their website (Loy and Eklundh, 2006), and
have additionally implemented ourselves the classic
method by Reisfeld et al. (Reisfeld et al., 1995).
Concerning the latter algorithm, it should be noted
that Reisfeld at al. gave different formulas for the ro-
tational symmetry score in (Reisfeld et al., 1990) and
(Reisfeld et al., 1995). We have implemented both to
allow for a comparison between these formulas. In
both of Reisfeld’s symmetry measures, contributions
by a point ~p with mirror point ~p
0
are weighted with a
factor exp(−k~p − ~p
0
k/2σ), which suppresses contri-
butions of points far away from the symmetry center.
Reisfeld et al. made no suggestion how to choose the
parameter σ, which must be related to the radius r
of the symmetric objects to be looked for
2
. We have
used the relation r = 2σ and, for performance rea-
sons, have cut off contributions of points at a distance
greater than 3σ. As our ground truth data contained
the actual object radius r, we have used this radius as
the input parameter for each particular image.
To see whether a logarithmic gradient transforma-
tion actually has the positive effect conjectured by Re-
isfeld et al., we have created their and our symmetry
transform both on the raw gradient image and on the
gradient image that has been transformed according to
Eq. (3). In addition to the method by Loy & Eklundh,
this resulted in a total of seven different algorithms
that we could run on our test data.
All of these symmetry transforms do not uniquely
yield symmetry points, but only symmetry scores
(or “votes”) for which there is no absolute criterion
whether a score actually represents a symmetry or not.
To avoid the introduction of a threshold on the sym-
metry score that is to a certain degree arbitrary, we
have therefore evaluated the symmetry detection on
basis of the highest symmetry score in the image. For
the methods by Reisfeld at al. and Loy & Eklundh,
the highest score value in the image should represent
2
The impact of the choice of σ in relation to the object
size would have been an interesting subject of investigation
in itself, that was however beyond the scope of the present
study. We settled on r = 2σ with the following reasoning:
The weight given to all pixels of an object with radius
r in Reisfeld’s et al. symmetry score is proportional to
2π
R
r
0
se
−s/σ
ds = 2πσ
2
(1−(1+r/σ)e
−r/σ
). Setting r = 2σ
results in a weight of 60% for the object; smaller values for
σ increase this ratio, but would suppress contributions from
near the object contour too much.
DetectionofSymmetryPointsinImages
581

Figure 5: Some input images (left) and the corresponding symmetry transforms and detected symmetry points highlighted in
green (right). The red points are local maxima with a higher symmetry score that have been rejected due to a too high “edge
directedness”.
the dominant rotational symmetry. In the case of our
method, we have sorted out the axial symmetries with
the following algorithm:
1. Find all local maxima in the symmetry transform
and sort them by their score value in descending
order.
2. Find the highest score value in this list that has an
“edge directedness” less than 0.27, which is an in-
dicator for a rotational symmetry instead of an ax-
ial symmetry, according to the results of Sec. 4.1.
Fig. 5 shows for sample images from our test set both
the resulting highest score and the higher scores that
have been sorted out by the second criterion.
Results on the CVPR 2011 Data Set. The CVPR
2011 data set was used at the workshop on symmetry
detection at CVPR 2011 for comparing two yet un-
published algorithms by Kim & Lee & Chee and by
Kondra & Petrosino with the algorithm by Loy & Ek-
lundh (Loy and Eklundh, 2006) . It consists of 42 im-
ages (including 4 doublets) of a size about 200 × 150
that had been harvested on the Internet; it includes
ground truth data of the symmetry centers and the
axes length of the elliptic symmetry regions.
In the experiments reported in (Rauschert et al.,
2011), the algorithms returned more than one symme-
try point per image and Rauschert et al. reported both
a recall and a precision value. As we only take into ac-
count the highest symmetry count, we can only mea-
0.10 0.2 0.3 0.4 0.60.5
Kondra Petrosino*
Kim, Lee, Chee*
Loy, Eklundh*
Loy, Eklundh
Reisfeld 90 (log)
Reisfeld 90
Reisfeld 95 (log)
Reisfeld 95
Our method (log)
Our method
Figure 6: Recognition rates of the tested algorithms on the
CVPR 2011 data set. Values with an asterisk are the preci-
sion values reported in (Rauschert et al., 2011).
sure the recognition rate as a precision value, i.e. the
number of returned symmetry points that actually cor-
respond to a ground truth symmetry. We have consid-
ered a symmetry to be found when the detected sym-
metry point had a distance less than 5 pixels from a
ground truth symmetry center.
The measured values for our algorithm and the al-
gorithm by Reisfeld et al. together with the results
reported in (Rauschert et al., 2011) can be seen in
Fig. 6. As our recognition rate is computed slightly
different from the precision value by Rauschert et al.,
we have given both values for the algorithm by Loy
& Eklundh, which shows that both rates are compara-
ble observables. The results show that our method is
comparable to the best method from the CVPR 2011
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
582

Table 1: Symmetry recognition rates on our test set for the different algorithms on different image categories (“Detail” etc.).
“grad” means that the gradient image has been used, while “log” means that the gradients have been transformed according
to Eq. (3).
Our method Reisfeld 95 Reisfeld 90 Loy &
Count grad log grad log grad log Eklundh
Detail 83 0.60 0.53 0.33 0.22 0.41 0.40 0.37
Context 76 0.33 0.39 0.18 0.20 0.37 0.36 0.37
Front 43 0.70 0.63 0.42 0.30 0.53 0.49 0.70
Light skew 57 0.58 0.53 0.25 0.14 0.47 0.40 0.39
Strong skew 59 0.20 0.29 0.15 0.20 0.20 0.27 0.12
Total 159 0.47 0.47 0.26 0.21 0.39 0.38 0.37
(a) Gradient absolute values. (b) Gradient absolute values after applying Eq. (3).
(c) Symmetry transform based on (a). (d) Symmetry transform based on (b).
Figure 7: Effect of the logarithmic gradient transformation according to Eq. (3) on a sample image from our own data set.
The detected symmetries by our algorithm are highlighted in green.
workshop. A closer look at the individual images
showed that our algorithm performed best on the 15
images with C
∞
symmetries (0.73 versus 0.60 by Loy
& Eklundh), which is easily understandable as the
discrete C
n
symmetries also include some odd n, for
which our algorithm is less suited. Due to the small
number of images, this difference in the recognition
rate is however of limited significance. It is interest-
ing to observe that a gradient transformation accord-
ing to Eq. (3) did not improve the symmetry detection,
but deteriorated the total recognition rate slightly. A
possible explanation can be that this transformation
amplifies background and noise edges, as can be seen
in Fig. 7.
Results on our Own Data Set. To test the robust-
ness of the algorithms with respect to skew and back-
ground noise on a larger data base, we have addition-
ally run the algorithms on our own data set. Due to
the larger image size, we have here considered a sym-
metry point as correctly detected when the resulting
point had a distance less than 10 pixels from a ground
truth symmetry point.
The recognition rates of correctly detected sym-
metry points in Tbl. 1 show, somewhat surprisingly,
that the later 1995 method by Reisfeld et al. per-
formed poorer than their 1990 method, a difference
that was even significant for a significance level of 5%
according to McNemar’s test (Diettrich, 1998). Our
new method was better than the 1990 method by Re-
isfeld. Again, the gradient transformation according
to Eq. (3) deteriorated the symmetry detection. As the
deteriorating effect can be observed on both different
tested data sets, we conclude that the logarithmic nor-
DetectionofSymmetryPointsinImages
583

(a) (b)
(c) (d)
(e) (f)
Figure 8: Some input images and the detected dominant rotational symmetry by our algorithm (green squares), and the
algorithms by Reisfeld et al. 1990 (red diamonds) and Loy & Eklundh (yellow circles).
malization of the gradient cannot be recommended for
symmetry detection.
Of all tested algorithms, the new method per-
formed on average even better than the algorithm by
Loy & Eklundh, which had shown the best perfor-
mance in the studies (Park et al., 2008) and (Rauschert
et al., 2011). As the varying results for the cate-
gories front/skewed show, the recognition rates of all
algorithms are lower for skewed rotation symmetries.
The algorithm by Loy & Eklundh is most suscep-
tible to distortion due to perspective: for unskewed
symmetries it shows the same performance as our al-
gorithm, but with skew the recognition rates become
even lower than those of the algorithm by Reisfeld et
al.. This is presumably due to the fact that a rotational
symmetry no longer holds in this case, but approxi-
mately becomes a C
2
mirror symmetry, which is still
detected by our method. Under stronger skew, this
approximation no longer holds and our method also
fails to detect most symmetries.
Fig. 8 shows exemplary results of all three al-
gorithms on images from our data set. There were
a number of images on which all three algorithms
worked well (like 8(a)), as well as images on which
all algorithms failed (e.g. due to a too strong skew
like in 8(f)). Neither algorithm was however consis-
tently better than a different algorithm on all images:
for each algorithm, there were images on which it was
the only one that detected a symmetry (see 8(b)-8(d)).
5 CONCLUSIONS
The new symmetry transform proposed in this paper
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
584

is very easy to implement and has shown a symmetry
detection rate that was both better than the algorithm
by Loy & Eklundh and than the symmetry transform
by Reisfeld et al. Even though the qualitative runtime
complexity of O(nr
2
) is similar to the latter algorithm,
with n the number of image pixels and r the maximum
radius, the absolute runtime of the new method is
lower because the symmetry score computation only
involves scalar products. While the method primarily
computes a point reflection symmetry (C
2
symmetry)
score, these can be discriminated into axial and rota-
tion symmetries with a criterion for the “edge direct-
edness” in the symmetry transform around the sym-
metry point.
For the method by Reisfeld et al., our experiments
have shown interesting results: first that the rotational
symmetry score RS proposed in their later paper (Re-
isfeld et al., 1995) performed worse than the score
CS from their earlier paper (Reisfeld et al., 1990).
Moreover, the logarithmic transformation of the gra-
dients did not have the positive effect that Reisfeld
at al. have conjectured, which leads to the question
whether other transformations might be helpful. To-
gether with the question of an optimal choice for the
parameter σ, these are interesting points that require
more detailed investigations.
For the new symmetry transform, there are also
a number of interesting open questions for future re-
search. One is the evaluation and optimization of the
automatic radius detection. Others are the extension
of the radius detection to rectangular symmetric re-
gions, or the effect of other gradient transformations.
Another important question for every kind of symme-
try transform is what absolute criteria actually deter-
mine a symmetry point, a problem that we have cir-
cumvented in the present study by using the relative
criterion of the highest score in the image.
It should be noted that the application of the new
symmetry transform is not necessarily restricted to
symmetry detection. It may also be a useful starting
point for feature extraction from images.
REFERENCES
Diettrich, T. (1998). Approximate statistical tests for com-
paring supervised classification learning algorithms.
Neural Computation, 10:1895–1923.
Gonzalez, R. and Woods, R. (2002). Digital Image Process-
ing. Prentice-Hall, New Jersey, 2nd edition.
Kanade, T. (1981). Recovery of the three-dimensional
shape of an object from a single view. Artificial In-
tellgence, 17:409–460.
Kuehnle, A. (1991). Symmetry-based recognition of vehi-
cle rears. Pattern recognition Letters, 12:249–258.
Lee, S. and Liu, Y. (2010). Skewed rotation symmetry
group detection. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 32(2):1659–1671.
Liu, Y., Hel-Or, H., Kaplan, C., and Gool, L. V. (2009).
Computational symmetry in computer vision and
computer graphics. Foundations and Trends in Com-
puter Graphics and Vision, 5:1–195.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 10(2):91–110.
Loy, G. and Eklundh, J. (2006). Detecting symmetry and
symmetric constellations of features. In European
Conference on Computer Vision (ECCV), pages 508–
521.
Loy, G. and Zelinsky, A. (2003). Fast radial symmetry for
detecting points of interest. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 25(8):959–
973.
Park, M., Lee, S., Chen, P., Kashyap, S., Butt, A., and Liu,
Y. (2008). Performance evaluation of state-of-the-art
discrete symmetry detection algorithms. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 1–8.
Rauschert, I., Brockelhurst, K., Liu, J., Kashyap, S., and
Liu, Y. (2011). Workshop on symmetry detection from
real world images - a summary. In IEEE Conference
on Computer Vision and Pattern Recognition (CVPR).
Reisfeld, D., Wolfson, H., and Yeshururn, Y. (1990). Detec-
tion of interest points using symmetry. In 3rd Interna-
tional Conference on Computer Vision, pages 62–65.
Reisfeld, D., Wolfson, H., and Yeshururn, Y. (1995).
Context-free attentual operators: The generalized
symmetry transform. International Journal of Com-
puter Vision, 14:119–130.
Tao, C., Shanxua, D., Fangrui, L., and Ting, R. (2009). Face
and facial feature localization based on color segmen-
tation and symmetry transform. In International Con-
ference on Multimedia Information Networking and
Security (MINES), pages 185–189.
DetectionofSymmetryPointsinImages
585
