An Agent-based Framework for Intelligent Optimization

of Interactive Visualizations

Pedro Miguel Moreira

1,2

, Lu

ıs Paulo Reis

2,3

and A. Augusto Sousa

ESTG-IPVC, School of Technology & Management, Polytechnic Institute of Viana do Castelo, Viana do Castelo, Portugal

LIACC-Artiﬁcial Intelligence and Computer Science Lab., Univ. of Porto, Porto, Portugal

EEUM-School of Engineering, Univ. of Minho-DSI, Campus de Azur

em, 4800-058 Guimar

aes, Portugal

INESC-TEC / DEI - Faculty of Engineering, Univ. of Porto, R. Dr. Roberto Frias, 4200-465 Porto, Portugal

Keywords:

Optimization, Multi-Agent Systems, Visualization.

Abstract:

Interactive visualization of virtual environments is an active research topic. There is a multiplicity of appli-

cations such as simulation systems, augmented and mixed reality environments, computer games, amongst

others, which endlessly demand for greater levels of realism and interaction. At every stage of the process,

including modeling, image synthesis, transmission and navigation, there are identiﬁable circumstances which

may compromise the achievement of high quality solutions for the posed problems. For many of these prob-

lems, an effective use of optimization tools can play a major role in order to achieve solutions with better

quality. Within this context, an innovative optimization architecture is presented regarding to two major prin-

ciples. The ﬁrst principle comprises the possibility to integrate, with reduced effort, the optimization tools with

existent applications and systems. Thus, we propose an agent-based framework where the optimization appli-

cation may operate as an independent process in respect to the visualization application where communication

is achieved by means of a speciﬁcally developed high-level message based protocol. The second principle

establishes on the utilization of a class of intelligent optimization methods, known as metaheuristics, which

major distinguishing quality is their great level of problem-independence, thus, enabling a wider application.

The paper describes conducted experiments and presents results that demonstrate the utility and efﬁcacy of the

proposed framework.

1 INTRODUCTION

There are many visualization related tasks in the con-

text of virtual environments that pose problems which

may beneﬁt from the adoption of optimization tools.

Although, the works found in the literature typically

tend to embed optimization deeply in the application.

Such course of action conducts, as a result, to design

and development efforts that are likely to have a lim-

ited reuse, besides the context for which they were

taken.

In this paper we introduce an agent based opti-

mization framework aiming to provide visualization

related problems the ability to interact with an opti-

mization agent in order to obtain optimized solutions.

The target applications are those that include some

kind of hard problems, e.g. combinatorial optimiza-

tion, for which there is not an efﬁcient algorithm to

achieve optimal solutions.

A key requirement of such agent-based framework

is to provide tools to attain, as much as possible, a

seamless integration to existing visualization appli-

cations or related algorithms. Thus, a minimal re-

design or re-code effort is expected in order to make

use and take beneﬁt of such tools. Besides, the agent

based architecture innately qualiﬁes for remote opera-

tion with respect to the optimizer and the applications.

Communication and interoperability is achieved via a

high-level message protocol over a standard (or exis-

tent) communication infrastructure (e.g. a computer

network with TCP/IP). The remote operation capabil-

ities open a wide range of application scenarios such

as the deployment on heterogeneous target platforms

(e.g mobile) or a better load balancing between op-

timization and visualization tasks using a distributed

architecture, as depicted by Figure 1.

The herein presented agent-based framework en-

deavors applicability and utility for a wide range of

distinct problems with reduced effort and signiﬁcant

levels of reuse. As a result, the strong decoupling

154

Moreira P., Reis L. and Sousa A..

An Agent-based Framework for Intelligent Optimization of Interactive Visualizations.

DOI: 10.5220/0004185301540159

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 154-159

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Optimizer I

(agent)

Optimizer II

(agent)

Visualization

Application II

(agent)

Visualization

Application I

(agent)

Figure 1: Agent-Based Optimization Architecture.

between the optimization process and the problem

comes into a major requirement. Ultimately, the

framework endeavors the application with a mini-

mal amount of domain speciﬁc knowledge. To fulﬁll

such requirements it is established on general purpose

intelligent optimization methods, speciﬁcally meta-

heuristics, that are made available through optimiza-

tion agents. Metaheuristics have several interesting

features(Blum and Roli, 2003), that can be summa-

rized as folllows: they guide the search process mak-

ing use of techniques ranging from basic local search

to complex learning processes; they are deﬁned at a

high level of abstraction, thus they are not problem-

speciﬁc; they can usually ﬁnd an optimal or near-

optimal solution in bounded time; they may use forms

of memory, thus beneﬁting from acquired search ex-

perience; they make use of randomized processes in

order to promote diversiﬁcation and to increase ro-

bustness; and they are often inspired by natural phe-

nomena (biological, physical, ethological, etc).

2 FRAMEWORK DESIGN

This section introduces the agent-based framework

design methodology, stating its main principles, goals

and requirements. The main requirements of the pro-

posed optimization framework are based on the fol-

lowing observations:

• There are many problems related to visualization

and rendering tasks that can beneﬁt from the use

of optimization. Some of these problems are dif-

ﬁcult in the sense that there is not a known algo-

rithm that can obtain optimal solutions efﬁciently.

• In the visualization and computer graphics do-

mains, researchers often develop their own opti-

mization systems. This happens mainly because,

as there is not any generic framework, it turns eas-

ier to develop a good optimization system from

scratch. However, having such a generic op-

timization system shall enable the developer to

test using different optimization methodologies

for each visualization problem.

• When used, optimization techniques are tightly

and deeply entangled in the visualization or ren-

dering algorithms resulting in an increased intri-

cacy of them. As this course of action does not

promote code and design reuse, bigger efforts are

required to test different optimization techniques

and to apply similar optimization techniques to

new problems.

• Graphical applications are regularly computation-

ally intensive. Moreover, optimization applica-

tions are also computationally intensive. There-

fore, the separation of the visualization from the

optimization tasks may be a way to improve the

overall performance. These tasks may be exe-

cuted at different machines (or cores) enabling the

the workload to be distributed and increasing the

overall performance thus.

As a result, and in order to overcome the afore-

mentioned problems and limitations, the proposed

methodology has the following fundamental princi-

ples, which will be further developed in the next sec-

tions respecting to the design and implementation.

The optimization process must:

• Be as independent as possible from the applica-

tion domain to permit its applicability to a wide

range of problems;

• Provide a conceptual decoupling from the visual-

ization application;

• Be implemented as autonomous agents; provide

with suitable interoperability and communication

mechanisms;

• Provide a set of algorithms and tools to make pos-

sible to test and compare the application of differ-

ent algorithms and parameters;

• Permit the easy integration and reuse of new opti-

mization algorithms and modules.

3 FRAMEWORK

IMPLEMENTATION

The framework core architecture is composed of six

core sets of classes, in respect to their responsibility

on the optimization process. The proposed and im-

plemented architecture is depicted in Figure 2. A de-

scription of each set of classes follows.

MetaHeuristics Classes. The MetaHeuristics set of

classes is deﬁned the different metaheuristics al-

gorithmic templates. These classes are explicitly

designed to do not have a particular representation

of the problem. They delegate on other classes

to perform generic actions, such as neighborhood

AnAgent-basedFrameworkforIntelligentOptimizationofInteractiveVisualizations

155

IOMFramework

erators

Metaheuristics

Data

Problem

Utility

iomGA iomHCiomSA

iomTerminatoriomCoolScheduler

...

iomIndividual iomRNG iomParser

iomProxyProblemiomProblem

...iomMove iomPopulation

Communication

iomClientiomServer

Figure 2: Core sets of classes.

selection, mutation, cross over, or termination cri-

teria. Implemented and available classes include

algorithmic templates for single point metaheuris-

tics, concretely Hill Climbing and Simulated An-

nealing(Kirkpatrick et al., 1983; Cern, 1985), and

also for a population based metaheuristic - Ge-

netic Algorithms(Holland, 1975). Variations to a

given metaheuristic can be achieved by instanti-

ating them with operators performing distinct be-

haviors or strategies. New metaheuristic algorith-

mic templates can be easily integrated into the

framework by inheriting from the abstract base

Metaheuristic class.

Operator Classes. Operators are mid level classes

which implement a vast set of components and

actions required by metaheuristics. Examples are

neighborhood explorers, termination criteria and

selection mechanisms. It is provided a set of ab-

stract template classes for each of these operators

together with a set of concrete classes implement-

ing commonly used operators.

Data Classes. This set of classes is designed to hold

of the basic data structures such as ﬁtness rep-

resentation, individuals (solutions are treated as

individuals with an associated ﬁtness value) and

moves. They have to be implemented in depen-

dence to the problem. Usual data representations,

such as vectors, are provided. Data classes are not

intended to be used as algorithmic components

and therefore they do not have any speciﬁc meth-

ods or functionality than those required related to

data handling and basic (problem dependent) op-

eration.

Problem Classes. Problem classes are deliberately

designed apart from the Metaheuristics to enable

an easy integration with an external application or

agent. They can be thought as the communica-

tion gateway between the optimizer and applica-

tion agents. They have three fundamental respon-

sibilities: hold a state of the problem; handle the

messages interchanged between the optimizer and

application; and evaluate solutions.

Communication Classes. These classes provide the

system with communication capabilities. The im-

plemented classes make use of TCP/IP sockets

and implement a custom communication protocol.

Utility Classes. In addition to the main core classes,

the framework also provides the user with a set of

utility classes such as random number generation,

statistics, parsing, etc.

As mentioned before, a relevant and innovative

feature of this optimization framework is concerned

to the separated and autonomous execution of opti-

mizer and the application. Optimizer and application

are agents that can be executed on different machines

given that they are interconnected by some network

infrastructure.

Optimizer

Agent

(act as server)

Application

Agent

(act as client)

<problem> [params]

<notfinal> [solution]

<continue> [evaluation]

<final> [solution]

<bye>

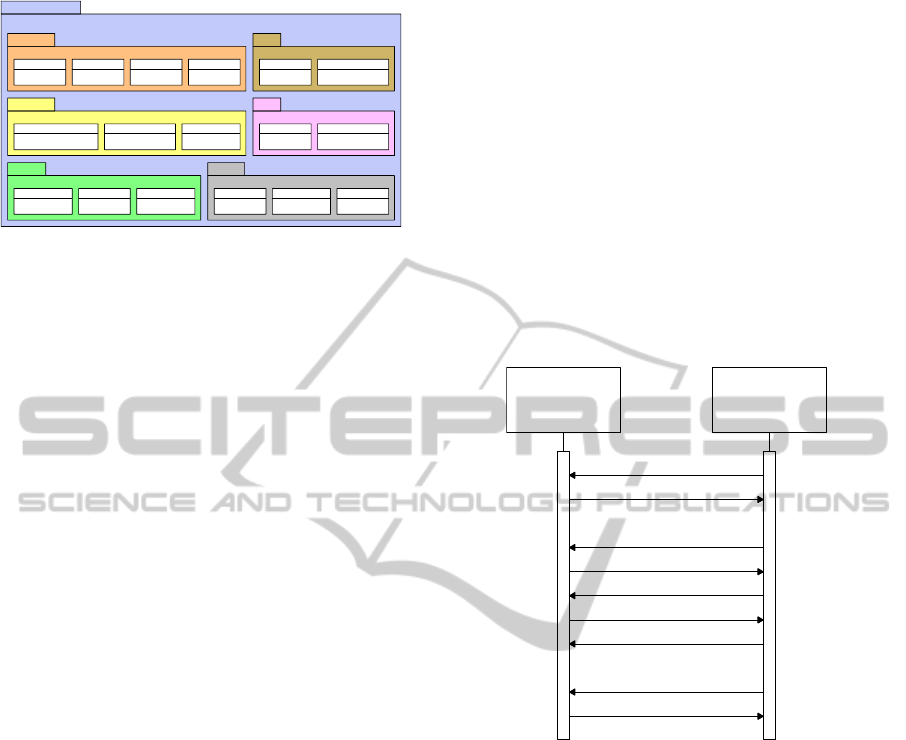
Figure 3: Communication Protocol.

A simple message protocol was designed in order

to support inter operation between the two classes of

agents (Figure 3). The protocol was intended to be

architecture independent, so it does not limit its ap-

plicability. The application agent acts as a client for

optimization purposes and initiates the connection by

sending a <connect> to the optimization agent, that

acts as a server. The optimizer agent responds with

a <connected> message, acknowledging the connec-

tion. The application agent then requests optimization

by means of a <problem> message encompassing pa-

rameters a problem description.

4 Experiments: Optimization of

Multiple View Selection

RoboCup was created as an international research and

education initiative, aiming to foster artiﬁcial intel-

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

156

ligence and robotics research, by providing a stan-

dard problem, where a wide range of technologies

can be examined and integrated (Kitano et al., 1997).

RoboCup Rescue project focus on urban disaster res-

cue. It aims at promoting research and development

by involving multi-agent team work coordination.

RoboCup Rescue competitions can be difﬁcult to

monitor and visualize as they comprise a complex and

dynamic environment (Certo et al., 2006).

Multi view visualizers intend to enable users and

team developers with a more effective understanding

of the on going action, since it is expected to auto-

matically provide a set of distinct views, selected in

order to optimize their relevance with respect to the

understanding of the evolving simulation.

Selecting multiple views in virtual environments

is interesting to many other applications. As, for in-

stance, virtual museums or tourism in order to gener-

ate a best set of views over a set of relevant objects, or

to generate paths for virtual exploration. Another rel-

evant example is virtual cinematography, in order to

automatically position, select and move virtual cam-

eras.

The best set of views can be formulated as an op-

timization problem and it was chosen to conduct a

ﬁrst set of experiments in order to test and validate the

previously described agent-based optimization frame-

work.

4.1 Problem Formulation

In the context of RoboCup Rescue, the best multi-

ple view problem can be informally stated as follows

(Moreira et al., 2006). In an urban rescue environ-

ment there are m visualization agents that can obtain

views over the scene. The problem is to ﬁnd the set

of k views that better describes the simulation at each

moment. The visualization agents are controllable in

the sense that one can affect their viewing parameters.

In order to formulate this problem as an optimization

problem, we developed a simple model for estimating

the quality of a multi-view. The devised multiview

quality is a function of the visibility, relevance, re-

dundancy and eccentricity of the entities represented

in the set of selected views. Thus, the corresponding

optimization problem can be formalized as follows:

MAXIMIZE:Q(MV ) =

∑

j=1

∑

i=1

Vis(e

) · Red(e

|MV ) · (W

.Rel(e

) −W

.Ecc(e

))

E = {e

,... e

};V = {v

,... v

}

= f (

Pos

V D

VU P

,FoV

) i ∈ {1, ...,m}

MV = {sv

,...,sv

} where MV ⊂ V and sv

6= sv

∀i 6= j

In the given formulation, E denotes the set of n

entities that have relevance in the scene (buildings,

agents, etc) and V is the set of different views (equals

the number of agents/entities with viewing capabili-

ties). Each view is characterized by usual camera pa-

rameters, as position

Pos

, view direction

V D

, rela-

tive camera orientation

VUP

and ﬁeld of view FoV

A multi-view, MV , comprises a set of k distinct

selected views (sv) from V .

The problem is to ﬁnd the optimal MV set, with

appropriate view parameters, that better describes the

rescue scenario given a quality metric. We developed

a quality Q metric using the following criteria (note

that e

denotes the visual properties of an entity e

a image obtained by the view j). The parameters W 1

and W 2 denotes constants used to adjust the relative

weight of relevance and eccentricity.

Visibility: Vis(e

). This feature relates to the visibil-

ity of the relevant entities (e.g. the visible area).

Several factors contribute to an entity’s visibility

such as the distance to the viewpoint, size, relative

orientation, and also by how much partial occlu-

sion it suffers from other objects.

Relevance: Rel(e

). A measure of how relevant is

the entity for the purpose of the visualization.

For example, if tracking emergency situations, a

building on ﬁre has a greater relevance than an un-

affected building. The intrinsic importance of an

object is also considered, e.g. hospitals, ﬁreman

headquarters, schools have more relevance than

ordinary buildings.

Redundancy: Red(e

|MV ). It is expected that the

multiple set of views describe as much as possi-

ble distinct situations occurring during the simu-

lation. Thus, redundant views over the same enti-

ties are penalized.

Eccentricity: Ecc(e

). A measure on how distant to

the center of the image an object is displayed.

This criterion has a perceptual foundation based

on the observation that an user will focus atten-

tion to image centered entities rather than to those

in more peripherical regions.

An expected multi-view is shown in Figure 4. As

it is depicted, regions with very intense ongoing res-

cue operations are shown with greater detail. Simulta-

neously other ares covered by wider views conﬁgured

in order to get a more comprehensive picture of (an

area) of the rescue scenario.

Using larger sets of views may be also of interest,

for instance, for surveillance centers, allowing to have

a better coverage of the ongoing operations either in

coverage either in detail. The above general problem

formulation was used in the experimental setup with

some simpliﬁcations. Namely, it was made W 2 = 0,

AnAgent-basedFrameworkforIntelligentOptimizationofInteractiveVisualizations

157

Figure 4: A multiview of a typical rescue scenario.

i.e. eccentricity was not considered, and agents were

provided with omnidirectional viewing abilities as it

is typical for RoboCup Rescue robots. Visibility was

evaluated as approximately proportional to the inverse

distance from the viewing entity to the viewed object,

accounting for maximimum visibility of all entities

near than 50 meters and null visibility for objects far

than 500 meters. This model, although not complete,

seems adequate with the viewing parameters used in

RoboCup Rescue operations.

4.2 Experimental Setup

In order to test the applicability of the optimization

methodoly and supporting architecture in respect to

visualization problems, preliminary tests were con-

ducted under the RoboCup Rescue domain in order to

optimize a set of views over a rescue simulation sce-

nario. For the purpose, simple RoboCup Rescue visu-

alization problems were used. These problems were

set up using distinct numbers of rescue entities (with

distinct abilities) and different numbers of agents with

viewing capabilities. Three different scenarios were

conﬁgured with respectively 500, 200 and 100 agents

with viewing abilities. For each of these scenarios

three different problem instances were tested in or-

der to ﬁnd the best set of 4, 10 and 20 views. Each

problem instance was solved by three different meta-

heuristics: Hill Climbing (HC); Simulated Annealing

(SA); and Genetic Algorithms (GA).

Each of the problems was solved using an evalua-

tion function ignoring eccentricity as was told before.

The evaluation function (Equation 1) uses visibil-

ity, relevance and redundancy. Redundancy is used

here in order to consider only the best view of each

entity as its global contribution to the evaluation func-

tion. Accounting for redundancy, has the purpose to

have a better coverage of the rescue arena, namely

by avoiding a selection of a set of similar views (cor-

Table 1: Experimental results using the second evaluation

function.



 Numberofentities



Number

ofviews

Algorithm 500 200 100



3099.96 1290.33 678.62

MEAN

3102.03 1291.53 679.55

MAX

HC

2.03 0.69 0.85

STDEV

3099.86 1289.34 679.55

MEAN

3102.97 1291.93 679.55

MAX

SA

3.82 3.18 0.00

STDEV

3101.10 1291.69 679.55

MEAN

3103.13 1291.93 679.55

MAX

20

GA

3.99 0.22 0.00

STDEV

2646.48 1170.16 593.94

MEAN

2654.90 1170.60 594.25

MAX

HC

10.17 0.60 0.36

STDEV

2650.63 1170.16 594.12

MEAN

2654.90 1170.60 594.25

MAX

SA

3.24 0.60 0.28

STDEV

2653.75 1170.60 594.25

MEAN

2654.90 1170.60 594.25

MAX

10

GA

2.58 0.00 0.00

STDEV

2206.53 892.94 442.80

MEAN

2207.21 892.94 442.80

MAX

HC

0.62 0.00 0.00

STDEV

2206.75 892.94 442.80

MEAN

2207.21 892.94 442.80

MAX

SA

0.62 0.00 0.00

STDEV

2207.21 892.94 442.80

MEAN

2207.21 892.94 442.80

MAX

4

GA

0.00 0.00 0.00

STDEV



responding to spatially close agents) focused on the

same entities.

MAXIMIZE:Q(MV ) =

∑

j=1

∑

i=1

Vis(e

) · Red(e

|MV ) ·W

· Rel(e

)

(1)

A set of initial experiments was performed in or-

der to tune the algorithms inherent parameters. For

the Hill-Climbing algorithm, a random neighbor ap-

proach was used with the neighborhood being gen-

erated by changing one of the viewing agents by an-

other. For Simulated Annealing, the same neighbor-

hood was used and an exponential cooling sched-

ule with an exponential ratio of 0.99 was used. For

Genetic Algorithms, an elitist selection mechanism

(keeping the best half of the population), single point

random crossover, and 10% of mutation probability

were used.

4.3 Experimental Results

A synthesis of the obtained results with the aforemen-

tioned evaluation function (Equation (1)) is presented

in Table 1 according to the described experimental

setup. The table displays the maximum (max), mean

and standard deviation (sd) values of ﬁve complete

experiments for each problem instance and algorithm.

Results analysis demonstrate that genetic algorithms

tend to achieve better global results, even using a sim-

ilar CPU time (GA parameters were conﬁgured in or-

der to use approximately the same CPU time as SA).

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

158

Simulated annealing is also able of achieving better

results if compared to the used hill-climbing.

1000

2000

0 1000 2000 3000 4000 5000

Figure 5: Graphical depiction of the achieved solution using

the second formulation for a problem with 500 20, where ∆

represent the selected viewing agents.

A graphical depiction of the solution is shown in

Figure 5. It can be concluded that the selected view-

ing agents are now spread around and able to cover

almost all the rescue arena. The set of solutions tend

to cover the most relevant regions without (or, at least,

less) repetition of the focused areas. Achieving good

solutions for this problem is difﬁcult mostly because

the multi view quality is a sum of interdependent

parcels. Results also demonstrated that the frame-

work is able of optimizing best multiple view prob-

lems and instances with different dimensions with re-

spect to the number of rescue entities and viewing en-

tities. Another conclusion is that the choice for sim-

pler metaheuristics, such as hill climbing, can achieve

good results. However, slightly different formulations

may lead to poor performance of this simpler algo-

rithm in respect to the quality of the achieved results.

5 DISCUSSION AND

CONCLUSIONS

We have described an agent-based intelligent opti-

mization framework designed to tackle several com-

plex problems within the visualization and rendering

domain.

Concurrently we have endorsed as a design goal

a high level of independence between the problem

solver and application, whic has been achieved intel-

ligent optimization (e.g. metaheuristics) as the core

of optimization engine.

The conducted experiments and results demon-

strate the suitability of the proposed approach

As future work it is intended to extend the pro-

posed framework with more optimization modules

such as Tabu Search (Glover, 1986), Ant Colony

Optimization (Dorigo and Stutzle, 2004) or Particle

Swarm Optimization (Kennedy and Eberhart, 1995).

A more challenging goal is to integrate capabilities

to negotiate among a community of distinct optimiza-

tion agents (e.g. providing distinct optimization meth-

ods) in order to obtain the best solution for a given

problem or set of problems. The application of the

proposed framework to other relevant problems, such

as the automatic path advice (And

ujar et al., 2004)

leading to assisted exploration of scenes within the

context of virtual environments is also envisioned.

REFERENCES

And

ujar, C., V

azquez, P., and Fair

en, M. (2004). Way-

ﬁnder: Guided tours through complex walkthrough

models. Computer Graphics Forum, 23(3):499–508.

Blum, C. and Roli, A. (2003). Metaheuristics in combinato-

rial optimization: Overview and conceptual compari-

son. ACM Computing Surveys, 35(3):268–308.

Cern, V. (1985). A thermodynamical approach to the travel-

ing salesman problem. Journal of Optimization The-

ory and Applications, 45(1):41–51.

Certo, J., Cordeiro, N., Reinaldo, F., Reis, L. P., and Lau,

N. (2006). Advances in Artiﬁcial Intelligence, vol-

ume vol. 26 of Research in Computing Science, chap-

ter FCPx: A Tool for Evaluating Teams’ Performance

in RoboCup Rescue Simulation League, pages 137–

148. National Polytechnic Institute.

Dorigo, M. and Stutzle, T. (2004). Ant Colony Optimiza-

tion. MIT Press.

Glover, F. (1986). Future paths for integer programming

and links to artiﬁcial intelligence. Computers & Op-

erations Research, 13(5):533–549.

Holland, J. H. (1975). Adaption in natural and artiﬁcial

systems. The University of Michigan Press, Ann Har-

bor.

Kennedy, J. and Eberhart, R. C. (1995). Particle swarm

optimization. In Proceedings of IEEE International

Conference on Neural Networks, pages 1942–1948.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. Science,

220(4598):671–680.

Kitano, H., Asada, M., Kuniyoshi, Y., Noda, I., Osawa, E.,

and Matsubara, H. (1997). RoboCup: A challenge

problem for AI. AI Magazine, 18(1):73–85.

Moreira, P. M., Reis, L. P., and de Sousa, A. A. (2006).

Best multiple-view selection: Application to the visu-

alization of urban rescue simulations. IJSIMM - Inter-

national Journal of Simulation Modelling, 5(4):167–

173.

AnAgent-basedFrameworkforIntelligentOptimizationofInteractiveVisualizations

159