2D-PAGE Texture Classification using Support Vector Machines

and Genetic Algorithms

An Hybrid Approach for Texture Image Analysis

Carlos Fernandez-Lozano

, Jose A. Seoane

, Pablo Mesejo

, Youssef S. G. Nashed

Stefano Cagnoni

and Julian Dorado

Information and Communications Technologies Department, University of A Coruña, Coruña, Spain

Department of Information Engineering, University of Parma, Province of Parma, Parma, Italy

Keywords: Texture Analysis, Feature Selection, Electrophoresis, Support Vector Machines, Genetic Algorithm.

Abstract: In this paper, a novel texture classification method from two-dimensional electrophoresis gel images is

presented. Such a method makes use of textural features that are reduced to a more compact and efficient

subset of characteristics by means of a Genetic Algorithm-based feature selection technique. Then, the

selected features are used as inputs for a classifier, in this case a Support Vector Machine. The accuracy of

the proposed method is around 94%, and has shown to yield statistically better performances than the

classification based on the entire feature set. We found that the most decisive and representative features for

the textural classification of proteins are those related to the second order co-occurrence matrix. This

classification step can be very useful in order to discard over-segmented areas after a protein segmentation

or identification process.

1 INTRODUCTION

Proteomics is the study of protein properties in a

cell, tissue or serum aimed at obtaining a global

integrated view of disease, physiological and

biochemical processes of cells and regulatory

networks. One of the most powerful techniques,

widely used to analyze complex protein mixtures

extracted from cells, tissues, or other biological

samples, is two-dimensional polyacrylamide gel

electrophoresis (2D-PAGE). In this method, proteins

are classified by molecular weight (MWt) and iso-

electric point (pI) using a controlled laboratory

process and digital imaging equipment.

Since the beginning of proteomic research, 2D-

PAGE has been the main protein separation

technique, even before proteomics became a reality

itself. The main advantages of this approach are its

robustness, its parallelism and its unique ability to

analyse complete proteins at high resolution,

keeping them intact and being able to isolate them

entirely (Rabilloud, Chevallet et al. 2010). However,

this method has also several drawbacks as its very

low effectiveness in the analysis of hydrophobic

proteins, as well as its high sensitivity to dynamic

range (i.e. quantitative ratio between the rarest

protein expressed in a sample and the most abundant

one) and quantitative distribution issues (Lu, Vogel

et al. 2007). The outcome of the process is an image

like the one showed in Figure 1.

Figure 1: Example image used to detect potential serum

protein biomarkers in children with fetal alcohol

syndrome. 512x512 pixels. 8 bit. 340 microns/pixel.

Taken from Lemkin public use dataset.

Dealing with this kind of images is a difficult

Fernandez-Lozano C., Seoane J., Mesejo P., S. G. Nashed Y., Cagnoni S. and Dorado J..

2D-PAGE Texture Classiﬁcation using Support Vector Machines and Genetic Algorithms - An Hybrid Approach for Texture Image Analysis.

DOI: 10.5220/0004187400050014

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 5-14

ISBN: 978-989-8565-35-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

task because there is not a commonly accepted

ground truth (Lemkin ; Marten). Another aspect that

makes the work difficult from a computer vision

point of view, is that both protein images and

background noise seem to follow a Gaussian

distribution (Tsakanikas and Manolakos 2009). The

inter- and intra-operator variability in manual

analysis of these images is also a big drawback

(Millioni et al., 2010).

The aim of this paper is to demonstrate that there

is enough texture information in 2D-electrophoresis

images to discriminate proteins from noise or

background. In this work the most representative

group of textural features are selected using Genetic

Algorithms.

2 THEORETICAL

BACKGROUND AND RELATED

WORK

The method proposed in this work intends to assist

in 2D-PAGE image analysis by studying the textural

information present within them. To do so, a novel

combination of Genetic Algorithms (Holland, 1975)

and Support Vector Machines (Vapnik, 1979) is

presented. In this section, the main techniques used

are briefly introduced and explained.

One of the most important characteristics used

for identifying objects or regions of interest in an

image is texture, related with the spatial (statistical)

distribution of the grey levels within an image

(Haralick et al., 1973). Texture is a surface’s

property and can be regarded as the almost regular

spatial organization of complex patterns, always

present even if they could exist as a non-dominant

feature. Other approaches (i.e. Structural which

represents texture by well-defined primitives and a

hierarchy of spatial arrangements. Model based

which using fractal and stochastic models, attempt to

interpret and image texture. Transform method such

as Fourier, Gabor or Wavelet transforms), within a

texture analysis, have been applied and a good

review can be found in (Materka and Strzelecki,

1998); (Tuceryan and Jain, 1999).

Genetic Algorithms (GAs) are search techniques

inspired by Darwinian Evolution and developed by

Holland in the 1970s (Holland, 1975). In a GA, an

initial population of individuals, i.e. possible

solutions defined within the domain of a fitness

function to be optimized, is evolved by means of

genetic operators: selection, crossover and mutation.

The selection operator ensures the survival of the

fittest, while the crossover represents the mating

between individuals, and the mutation operator

introduces random modifications. GAs possesses

effective exploration and exploitation capabilities to

explore the search space in parallel, exploiting the

information about the quality of the individuals

evaluated so far (Goldberg, 1989). Using the

crossover operator, GA combines the features of

parents to produce new and better solutions, which

preserve the parents’ best characteristics. By making

use of the mutation operator, new information is

introduced in the population in order to explore new

and promising areas of the search space. Another

strategy known as elitism, which is a variant of the

general process of constructing a new population, is

to allow better organisms from the current

generation to carry over the next, remaining

untalterd. At the end of the process, it is expected

that the population of solutions converges to the

global optimum.

Vapnik introduces Support Vector Machines

(SVMs) in the late 1970s on the foundation of

statistical learning theory (Vapnik, 1979). The basic

implementation deals with two-class problems in

which data are separated by a hyperplane defined by

a number of support vectors. This hyperplane

separates the positive from the negative examples, to

orient it such that the distance between the boundary

and the nearest data point in each class is maximal;

the nearest data points are used to define the

margins, known as support vectors (Burges, 1998).

These classifiers have also proven to be

exceptionally efficient in classification problems of

higher dimensionality (Chapelle et al., 1999);

(Moulin et al., 2004), because of their ability to

generalize in high-dimensional spaces, such as the

ones spanned by texture patterns. SVM uses

different non-linear kernel functions, like

polynomial, sigmoid and radial basis function,

where the nonlinear SVM maps the training samples

from the input spaces into a higher-dimensional

feature space via a mapping function (Burges, 1998).

With respect to related work, the authors were

not able to find any other work in the literature

handling with evolutionary computation in

combination with texture analysis in 2D-

electrophoresis images; however, one article

describes a discriminant partial least squares

regression (PLSR) method for spot filtering in 2D-

electrophoresis (Rye and Alsberg, 2008). They use a

set of parameters to build a model based on texture,

shape and intensity measurements using image

segments from gel segmentation. As regards texture

information, they have focused on descriptors

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

related to the noisy surface texture of unwanted

artefacts and concluded that their textural features

allow them to distinguish noisy features from protein

spots. In this work, five out of the eleven second-

order textural features, from the Grey Level Co-

Ocurrence Matrix (GLCM) firstly proposed by

Haralick, are used, and five new textural features

accounting for intensity relationships among sets of

three pixels. They distinguish proteins in the image

by using shape information, since cracks and

artefacts in gel surface deviate from a circular shape.

Besides that, a degree of Gaussian fit is calculated as

an indication of whether the image segment

corresponds to a protein or an artefact. Thereby

textural features are used for noise and crack

detection and as a complement for spot

segmentation. Finally, the 17 initial variables are

reduced to five PLSR components to account for

85% of the total variation with respect to the

response factor, and 82% of the total variation in the

data matrix.

3 MATERIALS

In order to generate the dataset, ten 2D-PAGE

images enough representative of different types of

tissues and different experimental conditions were

used. These images are similar to the ones used by

G.-Z. Yang (Imperial College of Science,

Technology and Medicine, London). It is important

to notice that Hunt et al. (Hunt et al., 2005)

determined that 7-8 is the minimum acceptable

number of samples for a proteomic study.

For each image, 50 regions of interest (ROIs)

representing proteins and 50 representing no-

proteins (noise, black non-protein regions, and

background) were selected to build a training set

with 1000 samples in a double-blind process in the

way that two clinicians select as many ROIs as they

considered and after that, within the common ROIs

clinicians selected proteins which are representatives

(isolated, overlapped, big, small, darker, etc.). For

each element, as will be seen later, 296 texture

features are computed.

The ROIs were selected taking into consideration

that, for each manually selected protein, there is an

area of influence surrounding it. It means that, once

the clinician has selected a protein, the ROI is

slightly bigger than the visible dark surface of such a

protein. This assumption is made because texture

could exist not only in the darkest grey levels but

also in the grey levels closest to white.

As said before, proteins seem to fit a Gaussian

peak, and ideally the center of the protein is in the

darkest zone of that peak. This approach prevents

the loss of information caused by neglecting the

lowest values of the inverted protein (grey levels

closest to white) that also fit the Gaussian peak. This

information could be useful to classify a protein or

to discard it.

4 PROPOSED METHOD

This paper goes further than related work in the

texture analysis of 2D-electrophoresis images,

studying the ability of textural features to

discriminate not only cracks from proteins but

background and no-protein dark spots as well.

The first step in texture analysis is texture feature

extraction from the ROIs. With a specialized

software called Mazda (Szczypinski et al., 2007),

296 texture features are computed for each element

in the training set. Various approaches have

demonstrated the effectiveness of this software

extracting textural features in different types of

medical images (Bonilha et al., 2003); (Létal et al.,

2003); (Mayerhoefer et al., 2005); (Harrison et al.,

2008); (Szymanski et al., 2012).

These features (Szczypiski et al., 2009), reported

in Table 1, are based on:

 Image histogram

 Co-ocurrence matrix: information about the grey

level value distribution of pairs of pixels with a

preset angle and distance between each other.

 Run-length matrix: information about sequences

of pixels with the same grey level values in a

given direction.

 Image gradients: spatial variation of grey level

values.

 Autoregressive models: description of texture

based on statistical correlation between

neighbouring pixels.

 Wavelet analysis: information about the image

frequency content at different scales.

Thus, from each ROI, texture information was

analyzed by extracting first and second-order

statistics, spatial frequencies, co-occurrence matrices

and two other statistical methods as autoregressive

model and wavelet based analysis, preserving the

original gray-level and spatial resolution on all runs.

Histogram-related measures conform the first-order

statistics proposed by Haralick (Haralick et al.,

1973) but second-order statistics are those derived

from the Spatial Distribution Grey-Level Matrices

2D-PAGETextureClassificationusingSupportVectorMachinesandGeneticAlgorithms-AnHybridApproachfor

TextureImageAnalysis

(SDGM). First-order statistics depend only on

individual pixel values and can be computed from

the histogram of pixel intensities in the image.

Second-order statistics depend on pairs of grey

values and on their spatial resolution. Additionally a

group of features derived from the textural ones is

also calculated, but cannot be used for texture

characterization such as the area of the ROI.

Table 1: Textural features extracted and used in this work.

Group Features

Histogram

Mean, variance, skewness, kurtosis,

percentiles 1%, 10%, 50%, 90% and

99%

Absolute

Gradient

Mean, variance, skewness, kurtosis and

percentage of pixels with nonzero

gradient

Run-length

Matrix

Run-length nonuniformity, grey-level

nonuniformity, long-run emphasis,

short-run emphasis and fraction of

image in runs

Co-ocurrence

Matrix

Angular second moment, contrast,

correlation, sum of squares, inverse

difference moment, sum average, sum

variance, sum entropy, entropy,

difference variance and difference

entropy

Autoregressive

Model

Theta: model parameter vector, four

parameters; Sigma: standard deviation

of the driving noise

Wavelet

Energy of wavelet coefficients in

subbands at successive scales; max

four scales, each with four parameters

All these feature sets were included in the

dataset. The normalization method applied was the

one set by default in Mazda: image intensities were

normalized in the range from 1 to Ng=2

, where k is

the number of bits per pixel used to encode the

image under analysis.

Two solutions are available for decreasing

dimensionality: extraction of new features derived

from the existing ones and selection of relevant

features to build robust models. In order to extract a

feature set from the problem data, principal

component analysis (PCA) has been commonly

used. In this work, GA is aimed at finding the

smallest feature subset able to yield a fitness value

above a threshold. Besides optimizing the

complexity of the classifier, feature selection may

also improve the classifiers’ quality. In fact,

classification accuracy could even improve if noisy

or dependent features are removed.

GAs for feature selection were first proposed by

Siedlecki and Skalansky (Siedlecki and Sklansky,

1989). Many studies have been done on GA for

feature selection since then (Kudo and Sklansky,

1998), concluding that GA is suitable for finding

optimal solutions to large problems with more than

40 features to select from.

GA for feature selection could be used in

combination with a classifier such SVM, k-nearest

neighbor (KNN) or artificial neural network (ANN),

optimizing it. In terms of classification accuracy

with imaging problems, SVMs have shown good

performance with textural features (Kim et al.,

2002); (Li et al., 2003); (Buciu et al., 2006), but also

KNN (Jain 1997) and hybrid approaches, which use

a combination of both classifiers (Zhang et al.,

2006), have obtained good results. Other techniques

use GA to optimize both the feature selection and

classifier parameters (Huang and Wang, 2006);

(Manimala et al., 2011).

In our method, based on both GA and SVM,

there are not a fixed number of variables. As the GA

continuously reduces the number of variables that

characterize the samples, a pruned search is

implemented. Each individual in the genetic

population is described by p genes (using binary

encoding). The fitness function (1) considers not

only the classification results but also the number of

variables used for such a classification, so it is

defined as the sum of two factors, one related to the

classification results and another to the number of

variables selected. In (1) the number of genes with a

true binary value (feature selected) is represented by

numberActiveFeatures. Regarding classification

results, it apparently gives better results taking into

account the F-measure than only using the accuracy

obtained with image features (Müller et al., 2008);

(Tamboli and Shah, 2011). F-measure (2) is a

function made up of the recall (true positives rate or

sensitivity: proportion of actual positives which are

correctly identified as such) and precision (or

positive predictive value: proportion of positive test

results that are true positives) measurements.

 



1









(1)

2.

. 

  

(2)

Therefore individuals with less active genes are

favored. Once the reduced feature dataset is

generated, a parametric test is made to evaluate the

adequacy of the feature selection process.

5 EXPERIMENTAL RESULTS

The test set is composed of ten representative

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

images for the different types of proteomic available

images, and for each one of them, 50 protein and 50

non-protein ROIs have been extracted to generate a

dataset with 1000 elements, that was divided

randomly in 800 elements, of which 600 elements

are used for training and 200 elements are used for

validation (inside the GA feature selection process)

and finally, 200 elements for test. Once the GA

finishes, the best individual found (the one with

lowest fitness value) is tested, using a 10-fold cross

validation (10-fold CV), to calculate the error of the

proposed model using the full and reduced datasets.

Then, a test set is used in order to evaluate the

adequacy of the reduction process.

Parameters domains of the feature selection

method are set as given in Table 2. These parameters

were initially adjusted based on the literature.

Table 2: Domain of GA tested parameters and operators.

Item Domain

Population Size From 100 to 250

Elitism From 0 to 2 %

Crossover probability From 80 to 98 %

Mutation probability From 1 to 5 %

Crossover operators

One-point crossover, two-point

crossover, scattered, arithmetic,

heuristic

Selection function

Uniform, roulette and

tournament

Mutation function Uniform, Gaussian

Different experiments have been performed and

the final combination set the population size to 250

individuals, with no elite, a 95% crossover

probability, a 2% mutation probability, with

crossover scattered, tournament selection and

mutation uniform.

SVM parameters domains are set as given in

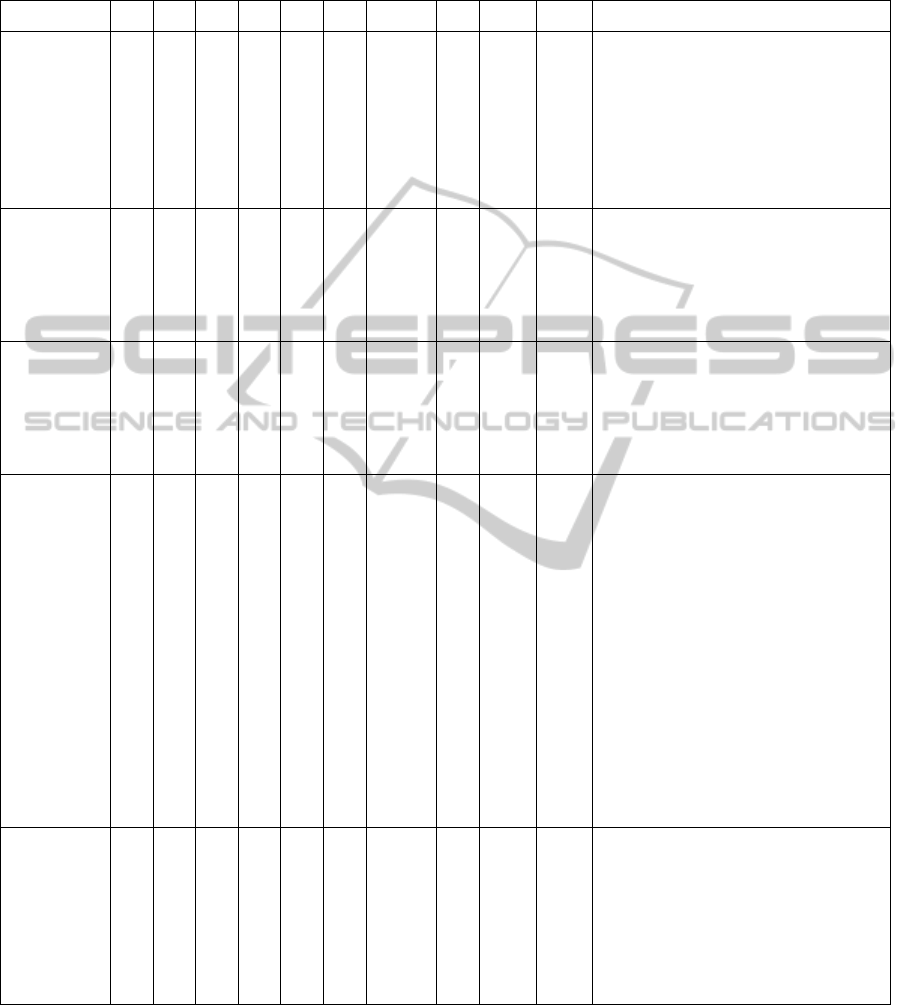
Table 3. The best results are shown in Table 4 in the

Appendix section. In the last column of this Table,

the final reduced textural features selected by the

GA-SVM combination is presented for each

configuration.

To evaluate the performance of this method,

there are several number of well-known accuracy

measures for a two-class classifier in the literature

such as: classification rate (accuracy), precision,

sensitivity, specificity, F-score, Area Under an ROC

Curve (AUC), Youden’s index, Cohen’s kappa,

likelihoods, discriminant power, etc. An

experimental comparison of performance measures

for classification could be found in (Ferri et al.,

2009). In (Huang and Ling, 2005), the authors

proposed that AUC is a better measure in general

than accuracy when comparing classifiers and in

general. The most common measures used for their

simplicity and successful application are the

classification rate and Cohen’s kappa measures.

Table 5 shows the results for classification rate

(accuracy), AUC, F-measure, Youden’s and

unweighted Cohen’s Kappa for each kernel. For this

problem, all the measures consider the same ranking,

and the best kernel function is the linear one. For

each kernel, Table 5 in the Appendix section shows

each feature in their textural membership group.

Table 3: SVM parameters domain.

Item Domain

Kernel function

Linear, quadratic,

polynomial and

Gaussian radial basis.

Gaussian radial basis sigma From 0.1 to 10

Gaussian radial basis C From 1 to 100

Polynomial order From 3 to 10

Method to find the hyperplane Quadratic programming

Among others, Mazda computes the area for

each ROI. This feature merely indicates the number

of pixels used for parameters computation. Being

strictly with a texture analysis process, it cannot be

used for texture characterization. With linear,

polynomial (order 3), and RBF (C=100 and

sigma=10) kernels, no textural features are selected

in order to select the most representative ones for

solving the classification problem. The presented

results seem to indicate that the textural group with

more representatives in 2D-PAGE images is the Co-

ocurrence matrix Group (second-order statistics).

As the proposed work intends to evaluate the

textural information present in a 2D-PAGE image,

the RBF(2) kernel function is selected as the most

accurate for solving this problem, since this kernel

has only textural features and the best rate in the

accuracy evaluation. After 45 generations, the GA

stopped because the stall condition was reached as

the best individual fitness value had not improved in

10 consecutive generations. Figure 2 reports the

number of features selected in each generation.

Figure 3 shows the evolution of the total number of

features, grouped by membership and selected

during GA generation.

We evaluate the reduced textural feature dataset

with the 200 elements reserved from the original

training set with the RBF (2) kernel, by calculating

the areas under the receiver operating characteristic

curves (AUC-ROCs) and a 10-fold CV for

separating the elements, using the Libsvm classifier

implementation (Chang and Lin, 2011) in Weka

(Hall et al., 2009) and comparing the results with the

2D-PAGETextureClassificationusingSupportVectorMachinesandGeneticAlgorithms-AnHybridApproachfor

TextureImageAnalysis

same classifier using the full dataset. Thus, we have

obtained samples composed by 10 AUC-ROC

measures. AUC-ROC area can be seen as the

capacity to be sensitive and specific at the same

time, in the sense that the bigger is the AUC-ROC,

the more accurate is the model. The ROC curve is a

graphical plot of the sensitivity against 1-specificity

as the detector threshold, or a parameter which

modifies the balance between sensitivity and

specificity.

Figure 2: Number of variables used in each GA

generation.

We use the RBF kernel with different gamma

values to check if there is a significant improvement

when the reduced dataset is used.

Figure 3: Evolution of feature number by group

membership during generations.

In order to use a parametric test, it is necessary to

check the independence, normality and

heteroscedasdicity (Sheskin, 2011). In statistics, two

events are independent when the fact that one occurs

does not modify the probability of the other one. An

observation is normal when its behaviour follows a

normal or Gaussian distribution with a certain value

of mean and variance. The heteroscedasticity

indicates the existence of a violation of the

hypothesis of equality of variances (García et al.,

2009).

With respect to the independence condition, we

separate the data using 10-fold CV. We perform a

normality analysis using the Shapiro-Wilk test

(Shapiro and Wilk, 1965) with a level of confidence

alpha=0.05, for the Null Hypothesis that the data

come from a normally distributed population. Null

hypothesis was rejected. The observed data fulfill

the normality condition, a Bartlett test (Bartlett,

1937) is performed in order to evaluate the

heteroscedasticity with a level of confidence

alpha=0.05.

A corrected paired Student’s t-test could be

performed in Weka (Hall et al., 2009), with a level

of confidence alpha=0.05, for the Null Hypothesis

that there are no differences between the average

values obtained by both methods. Results in average,

with standard deviation in brackets for AUC-ROC

are 0.94 (0.07) for the reduced dataset, and 0.55

(0.34) for the full dataset and the corrected paired

Student’s t-test determines that there is a significant

improvement in using the reduced dataset. The

reduced dataset has better accuracy result than the

full dataset. Even more, the corrected paired

Student’s t-test evaluates this improvement as

significant with an alpha=0.05.

Finally, the reduced textural features are the

following:

 Perc. (1)%

 S(2,-2)DifEntrp

 S(5,0) Correlat and InvDfMom

 S(0,5) DifVarnc

 S(5,5) SumEntrp

The 1% histogram percentile is a first order textural

feature calculated from the original image, taking

into account the intensity value and the frequency of

every pixel. Difference entropy, correlation, inverse

difference moment, difference variance and sum

entropy are second-order textural features. These

features evaluate the co-occurrence relationship

between pixels of the original image at a given

distance and angle. Hence, there is a relationship in

the co-occurrence matrix that allows the

discrimination of a protein in 2D-PAGE images.

6 SUMMARY AND

CONCLUSIONS

To the best of our knowledge, this is the first work

in which the classification of proteins texture in two-

dimensional electrophoresis gel images is tackled

using Evolutionary Computation, Support Vector

‐10

1 4 7 101316192225283134374043

Histogram(9)

Absolutegradient(5)

Run‐lengthmatrix(20)

Coocurrencematrix(221)

Autoregressivemodel(5)

Wavelet(15)

Notexturalfeatures(22)

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

Machines and Textural Analysis. In fact, this paper

demonstrates the existence of enough textural

information to discriminate proteins from noise and

background, as well as to show the potential of

SVMs in proteomic classification problems.

A new dataset with six features, starting from the

296 original ones, is created without loss of

accuracy, and the most representative textural group

is the Co-ocurrence matrix Group (second-order

statistics). In our experiments, the GLCM has

appeared as the best approximation for a good

classification of proteins in two-dimensional gel

electrophoresis. According to SVM, the 1%

histogram percentile, difference entropy, correlation,

inverse difference moment, difference variance and

sum entropy, are the most representative features for

solving this problem. A proper statistical test has

determined that there is a significant improvement in

using this reduced feature set with respect to the full

feature set.

ACKNOWLEDGEMENTS

This work is supported by the General Directorate of

Culture, Education and University Management of

the Xunta de Galicia (Ref. 10SIN105004PR). Pablo

Mesejo and Youssef S.G. Nashed are funded by the

European Comission (MIBISOC Marie Curie Initial

Training Network, FP7 PEOPLE-ITN-2008, GA n.

238819).

REFERENCES

Bartlett, M. S. (1937). "Properties of Sufficiency and

Statistical Tests." Proceedings of the Royal Society of

London. Series A, Mathematical and Physical

Sciences 160(901): 268-282.

Bonilha, L., E. Kobayashi, et al. (2003). "Texture Analysis

of Hippocampal Sclerosis." Epilepsia 44(12): 1546-

1550.

Buciu, I., C. Kotropoulos, et al. (2006). "Demonstrating

the stability of support vector machines for

classification." Signal Processing 86(9): 2364-2380.

Burges, C. J. C. (1998). "A tutorial on support vector

machines for pattern recognition." Data Mining and

Knowledge Discovery 2(2): 121-167.

Chang, C. C. and C. J. Lin (2011). "LIBSVM: A Library

for support vector machines." ACM Transactions on

Intelligent Systems and Technology 2(3).

Chapelle, O., P. Haffner, et al. (1999). "Support vector

machines for histogram-based image classification."

IEEE Transactions on Neural Networks 10(5): 1055-

1064.

Ferri, C., J. Hernádez-Orallo, et al. (2009). "An

experimental comparison of performance measures for

classification." Pattern Recognition Letters 30(1): 27-

38.

García, S., A. Fernández, et al. (2009). "A study of

statistical techniques and performance measures for

genetics-based machine learning: Accuracy and

interpretability." Soft Computing 13(10): 959-977.

Goldberg, D. (1989). Genetic Algorithms in Search,

Optimization, and Machine Learning, Addison-

Wesley Professional.

Hall, M., E. Frank, et al. (2009). "The WEKA data mining

software: an update." SIGKDD Explor. Newsl. 11(1):

10-18.

Haralick, R. M., K. Shanmugam, et al. (1973). "Textural

features for image classification." IEEE Transactions

on Systems, Man and Cybernetics smc 3(6): 610-621.

Harrison, L., P. Dastidar, et al. (2008). "Texture analysis

on MRI images of non-Hodgkin lymphoma."

Computers in Biology and Medicine 38(4): 519-524.

Holland, J. H. (1975). Adaptation in natural and artificial

systems: an introductory analysis with applications to

biology, control, and artificial intelligence, University

of Michigan Press.

Huang, C. L. and C. J. Wang (2006). "A GA-based feature

selection and parameters optimizationfor support

vector machines." Expert Systems with Applications

31(2): 231-240.

Huang, J. and C. X. Ling (2005). "Using AUC and

accuracy in evaluating learning algorithms." IEEE

Transactions on Knowledge and Data Engineering

17(3): 299-310.

Hunt, S. M. N., M. R. Thomas, et al. (2005). "Optimal

Replication and the Importance of Experimental

Design for Gel-Based Quantitative Proteomics."

Journal of Proteome Research 4(3): 809-819.

Jain, A. (1997). "Feature selection: evaluation, application,

and small sample performance." IEEE Transactions on

Pattern Analysis and Machine Intelligence

19(2): 153-

158.

Kim, K. I., K. Jung, et al. (2002). "Support vector

machines for texture classification." IEEE

Transactions on Pattern Analysis and Machine

Intelligence 24(11): 1542-1550.

Kudo, M. and J. Sklansky (1998). "A comparative

evaluation of medium- and large-scale feature

selectors for pattern classifiers." Kybernetika 34(4):

429-434.

Lemkin, P. F. ”The LECB 2D page gel image data set”,

from http://www.ccrnp.ncifcrf.gov/users/lemkin.

Létal, J., D. Jirák, et al. (2003). "MRI 'texture' analysis of

MR images of apples during ripening and storage."

LWT - Food Science and Technology 36(7): 719-727.

Li, S., J. T. Kwok, et al. (2003). "Texture classification

using the support vector machines." Pattern

Recognition 36(12): 2883-2893.

Manimala, K., K. Selvi, et al. (2011). "Hybrid soft

computing techniques for feature selection and

parameter optimization in power quality data mining."

Applied Soft Computing Journal 11(8): 5485-5497.

2D-PAGETextureClassificationusingSupportVectorMachinesandGeneticAlgorithms-AnHybridApproachfor

TextureImageAnalysis

Marten, R. "Marten Lab Proteomics Page." 2012, from

http://www.umbc.edu/proteome/image_analysis.html

Materka, A. and M. Strzelecki (1998). "Texture analysis

methods-A review." Technical University of Lodz,

Institute of Electronics. COST B11 report.

Mayerhoefer, M. E., M. J. Breitenseher, et al. (2005).

"Texture analysis for tissue discrimination on T1-

weighted MR images of the knee joint in a multicenter

study: Transferability of texture features and

comparison of feature selection methods and

classifiers." Journal of Magnetic Resonance Imaging

22(5): 674-680.

Millioni, R., S. Sbrignadello, et al. (2010). "The inter- and

intra-operator variability in manual spot segmentation

and its effect on spot quantitation in two-dimensional

electrophoresis analysis." Electrophoresis 31(10):

1739-1742.

Moulin, L. S., A. P. Alves Da Silva, et al. (2004).

"Support vector machines for transient stability

analysis of large-scale power systems." IEEE

Transactions on Power Systems 19(2): 818-825.

Müller, M., B. Demuth, et al. (2008). An evolutionary

approach for learning motion class patterns. 5096

LNCS: 365-374.

Rabilloud, T., M. Chevallet, et al. (2010). "Two-

dimensional gel electrophoresis in proteomics: Past,

present and future." Journal of Proteomics 73(11):

2064-2077.

Rye, M. B. and B. K. Alsberg (2008). "A multivariate spot

filtering model for two-dimensional gel

electrophoresis." Electrophoresis 29(6): 1369-1381.

Shapiro, S. S. and M. B. Wilk (1965). "An analysis of

variance test for normality (complete samples)."

Biometrika 52(3-4): 591-611.

Sheskin, D. J. (2011). Handbook of Parametric and

Nonparametric Statistical Procedures, Taylor and

Francis.

Siedlecki, W. and J. Sklansky (1989). "A note on genetic

algorithms for large-scale feature selection." Pattern

Recognition Letters 10(5): 335-347.

Szczypinski, P. M., M. Strzelecki, et al. (2007). MaZda - A

software for texture analysis.

Szczypiski, P. M., M. Strzelecki, et al. (2009). "MaZda-A

software package for image texture analysis."

Computer Methods and Programs in Biomedicine

94(1): 66-76.

Szymanski, J. J., J. T. Jamison, et al. (2012). "Texture

analysis of poly-adenylated mRNA staining following

global brain ischemia and reperfusion." Computer

Methods and Programs in Biomedicine 105(1): 81-94.

Tamboli, A. S. and M. A. Shah (2011). A Generic

Structure of Object Classification Using Genetic

Programming. Communication Systems and Network

Technologies (CSNT), 2011 International Conference

on.

Tsakanikas, P. and E. S. Manolakos (2009). "Improving 2-

DE gel image denoising using contourlets."

Proteomics 9(15): 3877-3888.

Tuceryan, M. and A. Jain (1999). Texture analysis.

Handbook of pattern recognition and computer vision,

World Scientific Publishing Company, Incorporated. 2.

Vapnik, V. N. (1979). Estimation of dependences based on

empirical data [in Russian]. Nauka, English

translation Springer Verlang, 1982.

Zhang, H., A. C. Berg, et al. (2006). SVM-KNN:

Discriminative nearest neighbor classification for

visual category recognition.

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

APPENDIX

Table 4: Results with different SVM kernel types.

TP FN FFP TN Acc AUC F-Meas Y’s Kapp Nvar Texture features

RBF(1) 90 10 18 82 0.86 0.86 0.8653 0.72 0.72 8

S(2,0)InvDfMom

S(0,3)SumAverg

S(0,3)DifVarnc

S(4,-4)Contrast

S(0,5)SumEntrp

S(0,5)DifEntrp

S(5,5)SumEntrp

S(5,-5)Entropy

RBF(2) 94 6 17 83

0.88

0.88 0.8909 0.77 0.77 6

Perc.01%

S(2,-2)DifEntrp

S(5,0)Correlat

S(5,0)InvDfMom

S(0,5)DifVarnc

S(5,5)SumEntrp

Linear 95 5 11 89 0.92 0.92 0.9268 0.85 0.85 6

Skewness

S(2,2)Correlat

S(4,0)InvDfMom

_Area_S(0,4)

S(5,0)Contrast

_Area_S(5,-5)

Poli(3) 87 13 19 81 0.84 0.84 0.844 0.68 0.68 16

Kurtosis

S(1,-1)Contrast

S(1,-1)DifEntrp

S(0,2)DifEntrp

S(0,4)SumAverg

S(4,-4)Correlat

S(4,-4)SumVarnc

S(5,0)InvDfMom

S(0,5)SumOfSqs

S(0,5)InvDfMom

S(0,5)SumEntrp

45dgr_GLevNoU

_AreaGr

GrKurtosis

WavEnLH_s-2

WavEnLH_s-4

RBF(100;10) 94 6 18 82 0.88 0.88 0.8867 0.76 0.76 8

_Area_S(0,1)

S(2,0)InvDfMom

_Area_S(5,0)

S(5,0)InvDfMom

S(0,5)InvDfMom

S(5,-5)DifEntrp

Horzl_GLevNonU

WavEnLH_s-4

2D-PAGETextureClassificationusingSupportVectorMachinesandGeneticAlgorithms-AnHybridApproachfor

TextureImageAnalysis

Table 5: Study of texture parameters between best SVM kernels in accuracy.

Histogram

Absolute gradient

Run-length matrix

Co-occurence matrix

Autoregresivve model

Wavelet

No texture feature

RBF(1)

S(2,0)InvDfMom

S(0,3)SumAverg

S(0,3)DifVarnc

S(4,-4)Contrast

S(0,5)SumEntrp

S(0,5)DifEntrp

S(5,5)SumEntrp

S(5,-5)Entropy

RBF(2) Perc.01%

S(2,-2)DifEntrp

S(5,0)Correlat

S(5,0)InvDfMom

S(0,5)DifVarnc

S(5,5)SumEntrp

Linear Skewness

S(2,2)Correlat

S(4,0)InvDfMom

S(5,0)Contrast

_Area_S(0,4)

_Area_S(5,-5)

Poli(3) Kurtosis GrKurtosis 45dgr_GLevNonU

S(1,-1)Contrast

S(1,-1)DifEntrp

S(0,2)DifEntrp

S(0,4)SumAverg

S(4,-4)Correlat

S(4,-4)SumVarnc

S(5,0)InvDfMom

S(0,5)SumOfSqs

S(0,5)InvDfMom

S(0,5)SumEntrp

WavEnLH_s-2

WavEnLH_s-4

_AreaGr

RBF(100;10)

Horzl_GLevNonU

S(2,0)InvDfMom

S(5,0)InvDfMom

S(0,5)InvDfMom

S(5,-5)DifEntrp

WavEnLH_s-4

_Area_S(0,1)

_Area_S(5,0)

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms