
A Flexible Particle Swarm Optimization based on Global Best and
Global Worst Information
Emre Çomak
Department of Computer Engineering, Pamukkale University, Denizli, Turkey
Keywords: Particle Swarm, Numerical Optimization, Linearly Increasing/Decreasing Inertia Weight, Global
Best/Worst Particle.
Abstract: A reverse direction supported particle swarm optimization (RDS-PSO) method was proposed in this paper.
The main idea to create such a method relies that on benefiting from global worst particle in reverse
direction. It offers avoiding from local optimal solutions and providing diversity thanks to its flexible
velocity update equation. Various experimental studies have been done in order to evaluate the effect of
variable inertia weight parameter on RDS-PSO by using of Rosenbrock, Rastrigin, Griewangk and Ackley
test functions. Experimental results showed that RDS-PSO, executed with increasing inertia weight, offered
relatively better performance than RDS-PSO with decreasing one. RDS-PSO executed with increasing
inertia weight produced remarkable improvements except on Rastrigin function when it is compared with
original PSO.
1 INTRODUCTION
With increasing demand for optimization algorithms
which employ at lower time costs and at less
computational burden, a number of methods have
been introduced. Particle Swarm Optimization is one
of the most effective swarm intelligence methods
theorized by (Kennedy and Eberhart, 1995).
PSO can be adapted for different problems in a
simple way, it is less likely to get trapped at local
optimal solutions, it can approximate to optimal
points quickly and it has the advantage of
cooperation between particles. These are superior
features of PSO in comparison with mathematical
algorithms. Therefore; it has been implemented in
many optimization applications (W. L. Du and B. Li,
2008; K. Tang and X. Yao, 2008).
Unlike these benefits, PSO has some
deficiencies. According to (Angeline, 1998), PSO
does not have a skill to perform a quality grain
search as the iteration index of generations
increases. Since velocity update equation of PSO
depends on only global best and personal best
positions, diversity of population in PSO decreases.
Thus; PSO may get trapped at local optimum. (P. N.
Suganthan, 1999) proposed a particle swarm
optimizer with neighborhood operator in order to
avoid this challenge. Moreover, a number of studies
have been suggested to improve general PSO
performance. (Chen and Zhao, 2009) proposed a
PSO with adaptive population size to build a new
PSO structure which has improved performance and
offered less computational cost. (Kennedy and
Mendes, 2002) investigated effects of population
topologies on performance of PSO. They assert that
some topologies employ well for a group of
functions and others for a different group. (Alatas et
al., 2009 and Coelho LdS, 2008) adopted chaotic
solutions to PSO in order to improve overall
performance of original PSO.
Global and local searching ability should be
adjusted in all optimization methods including PSO.
Some evolutionary algorithms regulate the trade-off
between global and local searching ability via
variance of Gaussian random function (Shi and
Eberhart, 2001). Inertia weight parameter was added
into PSO in order to overcome such a trade-off.
Setting the inertia weight to a large value increases
global searching ability, whereas smaller values
increase local one.
All approaches proposed in literature need some
extra computations in addition to regular PSO
computations. This paper proposes that adding
global worst particle to velocity update equation
may increase the diversity of PSO. Based on the
255
Çomak E. (2013).
A Flexible Particle Swarm Optimization based on Global Best and Global Worst Information.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 255-262
DOI: 10.5220/0004187602550262
Copyright
c
SciTePress

results of this study, a new regulation procedure will
be improved to increase the performance of this new
PSO. This proposal does not add extra
computational cost to PSO algorithm. Because it
only computes global worst particle in addition to
global best particle at all iterations. All other
computations are the same with traditional PSO.
Effects of inertia weight on new velocity update
equation have been investigated as well.
Rest of the paper is organized as follows.
Detailed description of PSO takes place in section 2.
Section 3 introduces reverse direction support
particle swarm optimization (RDS-PSO) run in 4
modes (1000 and 2000 maximal iterations with
increasing and decreasing inertia weights).
Simulation results of the proposed method on
benchmark problems are assessed in section 4.
Finally, section 5 is the discussion and the
conclusion part of the paper.
2 PARTICLE SWARM
OPTIMIZATION (PSO)
PSO is a searching and optimization method based
on sociologically and biologically inspired
procedures simulating bird flocking (Kennedy and
Eberhart, 1995). Each potential solution is
represented as a particle. A group of particles are
used to reach global optimal solution in PSO. Let N
and D be the population size and dimension of
search space, respectively. Then, the swarm can be
described by N particles which are represented by D
dimensional vector. Actual position of i
th
particle is
represented by
iDiii
xxxx ,...,,
21
and the velocity of it
is represented by
iDiii
vvvv ,...,,
21
. The vector,
iDiii
pppp ,...,,
21
, reflects the best visited position of
the particle i until the time of t. Iteration number
controls these running times.
idgd
idididid
xprandc
xprandcvwv
2...
...1
2
1
(1)
ididid
vxx
(2)
Where i = 1, 2, … , N and d = 1, 2, … , D.
Parameters c
1
and c
2
are positive constants denoting
cognitive and social impacts in PSO. The functions
of rand1 and rand2 generate random numbers in
interval [0, 1] uniformly. Positive parameter, w is
the inertia weight. As mentioned in introduction, w
regulates the trade-off between global and local
searching ability. Variables p
id
, p
gd
and x
id
represents
personal best, global best and present position,
respectively.
At each iteration, equations (1) and (2) are
computed repeatedly in original PSO. Some
strategies such as iteration number, improvement or
stability extent were proposed as various termination
criteria in literature. Since there is no unit to control
the velocities of particles in velocity update
equations, particles may pass over the borders of
search space. So, maximal velocity value, V
max
was
determined to avoid this situation. Velocities
exceeding the maximal velocity, V
max
, are set to
V
max
.
3 REVERSE DIRECTION
SUPPORTED PSO (RDS-PSO)
A more flexible and more general PSO, RDS-PSO,
is introduced in this part of the paper. In other
words, original PSO method is only a specific case
of RDS-PSO method. The single difference between
RDS-PSO and PSO relies on velocity update
equation.
gwdid
idgd
idididid
pxrandcalpha
xprandcalpha
xprandcvwv
21...
...2...
...1
2
2
1
(3)
RDS-PSO uses equation (3) instead of equation
(1). As a different variable from original PSO, p
gwd
represents the global worst position. The variable
p
gwd
is determined by the max operator in
minimization problems and by the min operator in
maximization ones. Unlike p
gd
, p
gwd
affects the
velocity update equation in reverse direction.
Another different parameter, alpha, provides a trade-
off between effects of global best and global worst
positions on next position of particle. It belongs to a
real number set and is defined in [0, 1]. When alpha
is selected with 1 value, the original PSO method
occurs. By selecting different alpha values, PSO can
be generalized. Thus; RDS-PSO provides a
flexibility to control passing from original PSO to
pure RDS-PSO. Regulating of alpha value properly
plays a very important role in success of RDS-PSO.
Figure 1 depicts original PSO velocity update and
figure 2 depicts RDS-PSO velocity update idea for
alpha = 0.5 value. In the case of alpha = 0.5, the
global best and the global worst particles have equal
effect on population. As the value of alpha closes to
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
256

zero, diversity may increase. However, the
performance of RDS-PSO deteriorates.
Evaluation function has already been run as in
PSO. RDS-PSO keeps only the worst position in
addition to the best position. Thus, computational
burden of RDS-PSO is almost same with PSO.
In the paper, relationship between inertia weight
and alpha parameter is evaluated by benchmark test
functions. This paper tries to find a response to the
question, “what is the best alpha value for RDS-PSO
with linearly increasing and linearly decreasing
inertia weight order?”. In addition, the paper
researches whether RDS-PSO increases the overall
performance of PSO or not. How can a regulation
approach be proposed for a better RDS-PSO
performance?
Figure 1: Velocity update for PSO.
Figure 2: Velocity update for RDS-PSO.
4 BENCHMARK PROBLEMS
AND EXPERIMENTAL
RESULTS
Section 4 explains mathematical background of
benchmark functions superficially and evaluates
experimental results.
4.1 Benchmark Functions
Four most commonly used benchmark functions
(Griewangk, Rastrigin, Rosenbrock and Ackley) are
used to test the performance of RDS-PSO against
PSO with linearly increasing and decreasing inertia
weight. As described in detailed in table 1, one of
them is unimodal (has only one optimum) and the
others are multimodal (have lots of optimum).
Where lb is abbreviated of lower bound, ub is
abbreviated of upper bound for space coordinates.
Effectiveness of proposed algorithms can be
evaluated via such 3 benchmark functions.
Table 1: Properties of benchmark functions.
Function lb ub Optimum point Modality
Griewangk -600 600 0 multimodal
Rastrigin -5.12 5.12 0 multimodal
Rosenbrock -2.048 2.048 0 unimodal
Ackley -32.786 32.786 0 multimodal
4.1.1 Griewangk Function
Griewangk function has lots of local optima. Due to
this reason, finding the global optimum point is a
very difficult task (Griewangk, 1981). This function
is described as in equation (4).
30
1
30
1
2
1cos
4000
i
i
i
i
i
xx
f x
(4)
Where
600,600
i
x
, global optimum point of
the function is at x = (0, 0,…,0) and f(x) = 0.
4.1.2 Rastrigin Function
Rastrigin function is obtained by adding cosine
modulation to De Jong’s function. Such a
modulation makes this function highly multimodal
(Rastrigin, 1974) and it is defined as an equation (5).
30
1
2
2cos103010
i
ii
xxf
x
(5)
AFlexibleParticleSwarmOptimizationbasedonGlobalBestandGlobalWorstInformation
257

Where
12.5,12.5
i
x
, global optimum point of
the function is at x = (0, 0,…,0) and f(x) = 0.
4.1.3 Rosenbrock Function
Rosenbrock function is also known as banana
function because of its shape. Due to difficulty in
finding global optimal of it, Rosenbrock function is
repeatedly used in testing of many optimization
algorithms (De Jong, 1975). This function is
described as in equation (6).
30
1
2
2
2
1
1100
i
iii
xxxf x
(6)
Where
048.2,048.2
i
x
, global optimum point
of the function is at x = (1, 1,…,1) and f(x) = 0.
4.1.4 Ackley Function
Ackley is widely used as a multimodal test function
in most optimization problems (D. H. Ackley, 1987).
Its description is given as following.
1expcos
1
exp...
...
1
exp
1
!
2
acx
n
x
n
baf
n
i
i
n
i
i
x
(7)
It is recommended that a = 20, b = 0.2, c = 2п.
768.32,768.32
i
x
, global optimum point of the
function is at x = (0, 0,…,0) and f(x) = 0.
4.2 Experimental Results
Overall performance of RDS-PSO method is
evaluated according to 3 benchmark functions. The
method were executed in 4 different modes so that,
RDS-PSO and PSO could be compared in a more
detailed way. These 4 modes include linearly
decreasing inertia weight with 1000 / 2000 iterations
and linearly increasing inertia weight with 1000 /
2000 iterations. All modes were executed with
variable alpha values changing from 0.05 to 1.0 with
0.05 step size. Thus, the most suitable alpha value
was searched in all modes. Matlab software was
used for programming.
50 different initial populations were set
randomly. The performance of RDS-PSO was tested
through average and standard deviation values of all
population results. Moreover, the number of
populations having better scores than PSO is
computed as well.
As it is indicated in table 2, population and
dimension sizes were defined as 25 and 10
respectively while maximal iteration index was
determined as 1000 in some experiments and as
2000 in others. The parameters of c
1
and c
2
are
cognitive and social constants, respectively. To be
increased of c
1
enhances exploration while to be
increased of c
2
enhances exploitation. According to
the most related studies, determining, c
1
= c
2
= 2,
provides the best performance for PSO
implementations. Inertia weight changes linearly
within the range [0.1, 1.2]. When error between
target and system output is smaller than 1*10
-6
,
process is stopped.
Table 2: Configuration of used PSO method.
Parameter Value
Population size 25
Maximal iteration 1000 / 2000
Maximal weight value 1.2
Minimal weight value 0.1
C
1
2.0
C
2
2.0
Dimension 10
Error goal 1*10
-6
By using of PSO configuration in table 2, three
types of result were obtained. First of them reflects
average best fitness results of 50 different situations.
These populations have different and independent
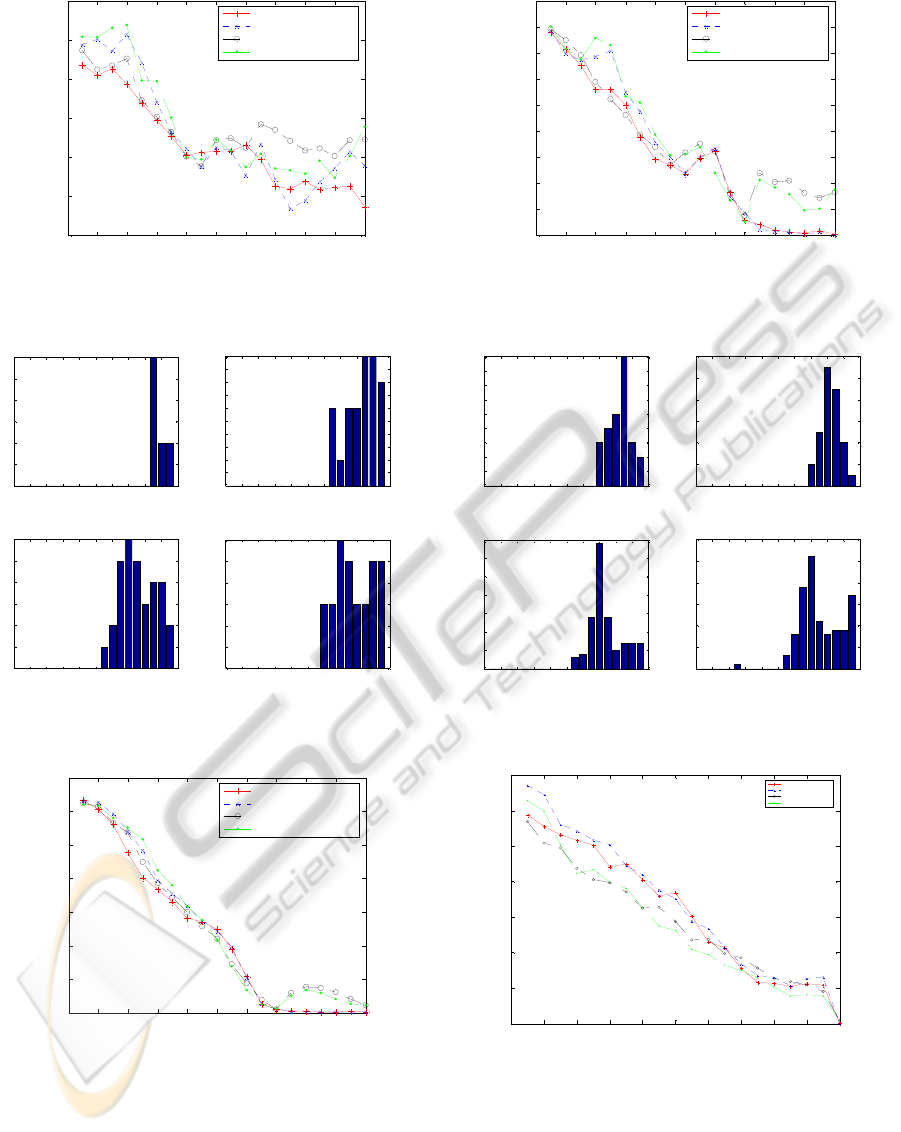
initial populations. Figure 3, 6, 9 and 12 depict such
results of 4 modes for Rosenbrock, Rastrigin,
Griewangk and Ackley test functions respectively.
The second type reflects average of standard
deviation results. Figure 4, 7, 10 and 13 depict such
results of 4 modes for the same four test functions
respectively. Finally the third type consists of
numbers of being better than original PSO. For
instance, at 9 situations among 50 RDS-PSO (with
decreasing inertia weight and 1000 maximal
iteration) has smaller best fitness value than PSO as
it is presented in figure 5(a). Such numbers are
depicted in figure 5, 8, 11 and 14 for the same test
functions respectively.
In all modes, average best fitness results of
original PSO are lower than RDS-PSO versions for
Rosenbrock, Rastrigin and Ackley functions as
depicted in figure 3, 6 and 9. In 2 modes (decreasing
inertia weight with 1000 / 2000 maximal iterations),
original PSO results are lower than RDS-PSO for
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
258

Griewangk function too. However; in the other 2
modes (increasing inertia weight with 1000 / 2000
maximal iterations), original PSO results are higher
than RDS-PSO ones (having 0.7 alpha value) for
Griewangk function as depicted in figure 9.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
500
1000
1500
2000
2500
3000
3500
4000
alpha
average best fittness results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 3: Average best fitness results of RDS-PSO for 4
modes using Rosenbrock function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
500
1000
1500
2000
2500
alpha
standard deviation results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 4: Average standard deviation results of RDS-PSO
for 4 modes using Rosenbrock function.
Figure 4 depicts that average standard deviation
results of original PSO are lower than RDS-PSO
versions in all modes for Rosenbrock function,
similarly as in average best fitness results. The same
results are also obtained for Ackley function as in
figure 13. Figure 7 states that original PSO has
lower average standard deviation values than RDS-
PSO in only one mode (decreasing inertia weight
with 1000 maximal iteration). In other modes
original PSO has higher values than RDS-PSO for
Rastrigin function. According to Griewangk
function results, original PSO has lower values in 2
modes (decreasing modes) yet higher values in other
2 modes (increasing modes) than RDS-PSO as
depicted in figure 10. At almost all modes except
that Rosenbrock function is used, RDS-PSO has
more stability than PSO.
0 0.1 0.2 0.3 0.4 0.5 0. 6 0.7 0.8 0.9 1
0
1
2
3
4
5
6
7
8
9
RDS-PSO with decreasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(a)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0. 6 0.7 0.8 0.9 1
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
RDS-PSO with decreasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(b)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
5
10
15
20
25
RDS-PSO with increasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(c)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
5
10
15
20
25
30
RDS-PSO with increasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(d)
number of being better than PSO
Figure 5: Number of being better than PSO for 4 modes
using Rosenbrock function.
Additionally; figures 5, 8, 11 and 14 state the
number of situations where original PSO has higher
best fitness value than the RDS-PSO version. In
increasing inertia weight modes, RDS-PSO has
relatively better results against decreasing inertia
weight modes. The most suitable contribution was
surveyed in Griewangk function among 3
benchmark functions. In 34 executions of 50,
original PSO has higher fitness (worse) results than
RDS-PSO (increasing inertia weight with 1000
maximal iteration and value of alpha is 0.7). The
worst situation was observed in figure 14 for Ackley
function.
At all test functions, RDS-PSO with increasing
inertia weight performs relatively better results
against ones running at decreasing modes. At the
same time, standard deviation results are relatively
better than decreasing ones when PSO is compared
with RDS-PSO versions.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
20
40
60
80
100
120
140
160
180
alpha
average best fittness results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 6: Average best fitness results of RDS-PSO for 4
modes using Rastrigin function.
AFlexibleParticleSwarmOptimizationbasedonGlobalBestandGlobalWorstInformation
259
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
5
10
15
20
25
30
35
alpha
standard deviation results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 7: Average standard deviation results of RDS-PSO
for 4 modes using Rastrigin function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.5
1
1.5
2
2.5
3
RDS-PSO with decreasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(a)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
RDS-PSO with decreasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(b)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
5
6
RDS-PSO with increasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(c)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
5
6
RDS-PSO with increasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(d)
number of being better than PSO
Figure 8: Number of being better than PSO for 4 modes
using Rastrigin function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
50
100
150
200
250
300
350
alpha
average best fittness results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 9: Average best fitness results of RDS-PSO for 4
modes using Griewangk function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
10
20
30
40
50
60
70
80
90
alpha
standard deviation results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 10: Average standard deviation results of RDS-
PSO for 4 modes using Griewangk function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
5
6
7
8
9
RDS-PSO with decreasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(a)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
2
4
6
8
10
12
RDS-PSO with decreasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(b)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
5
10
15
20
25
30
35
RDS-PSO with increasing inertia weight and 1000 maximal iteration
alpha [0.05-0.95]...(c)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
5
10
15
20
25
30
RDS-PSO with increasing inertia weight and 2000 maximal iteration
alpha [0.05-0.95]...(d)
number of being better than PSO
Figure 11: Number of being better than PSO for 4 modes
using Griewangk function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0. 7 0.8 0. 9 1
0
2
4
6
8
10
12
14
alpha
average best fittness results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 12: Average best fitness results of RDS-PSO for 4
modes using Ackley function.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
260

0 0.1 0. 2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
alpha
standard deviation results
+ 1000 max itr and dec w
x 2000 max itr and dec w
o 1000 max itr and inc w
. 2000 max itr and inc w
Figure 13: Average standard deviation results of RDS-
PSO for 4 modes using Ackley function.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
RDS-PSO wit h decreasing inertia weight and 1000 maxi mal iterat ion
alpha [0.05-0.9 5]...(a)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
RDS-PSO wit h decreasing inertia weight and 2000 maxi mal iterat ion
alpha [0.05-0.9 5]...(b)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
RDS-PSO w ith increasi ng inertia wei ght and 1000 max imal ite ration
alpha [0.05-0.9 5]...(c)
number of being better than PSO
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
RDS-PSO w ith increasi ng inertia wei ght and 2000 max imal ite ration
alpha [0.05-0.9 5]...(d)
number of being better than PSO
Figure 14: Number of being better than PSO for 4 modes
using Griewangk function.
Generally the performance of RDS-PSO is not good
as PSO but, its performance gets quality as the index
of generation increases.
5 DISCUSSION AND
CONCLUSION
In this paper, a variety of PSO, which is called RDS-
PSO, has been proposed. RDS-PSO tries to increase
the diversity of PSO by using reverse direct
information in velocity update equation. It does not
add any additional burden for computation since it
uses the same algorithm with original PSO.
Alpha constant was added to RDS-PSO as a
difference from PSO in order to provide a balance
between impacts of global best and global worst
particles. It plays an important role on overall
performance of RDS-PSO. According to
experimental results, alpha values in [0.65, 0.75]
performs the best performance for RDS-PSO in
increasing inertia weight modes while such values in
[0.8, 0.9] performs its best in decreasing one. If a
procedure which changes the alpha value during
execution properly is adopted to current algorithm,
overall performance of RDS-PSO will improve. As a
future research topic, such procedure might be
studied. Results of RDS-PSO with constant alpha
value are not quality as some studies manage, but an
RDS-PSO with adaptively changing alpha value
might be much more quality than constant one.
Selection of neighbourhood strategy affects the
performance of RDS-PSO as well. Such strategies
may be updated according to velocity equation of
RDS-PSO. Some topologies may be used for global
best neighbourhood while other topologies for
global worst one. Thus, both some best particles and
some worst particles in the neighbourhood can affect
the next position of particles in swarm in much
suitable way.
REFERENCES
Kennedy, J., Eberhart, R.C., 1995. Particle swarm
optimization. In Proceedings of the IEEE Conference
on Neural Networks. Australia, p. 1942-1948.
Du, W.L., Li, B., 2008. Multi-strategy ensemble particle
swarm optimization for dynamic optimization. In
Information Sciences 178(15), p. 3096-3109.
Tang, K., Yao, X., 2008. Special Issue on nature inspired
problem solving. In Information Sciences 178(15), p.
2983-2984.
Angeline, P., 1998. Evolutionary optimization versus
particle swarm optimization: philosophy and
performance difference. In Proceedings of
Evolutionary Programming Conference, San Diago
USA.
Suganthan, P.N., 1999. Particle swarm optimizer with
neighbourhood operator. In Proceedings of the 1999
Congress of Evolutionary Computation. IEEE Press,
volume 3, p. 1958-1962.
Chen, D.B., Zhao, C.X., 2009. Particle swarm
optimization with adaptive population size and its
application. In Applied Soft Computing volume 9,
p.39-48. Science Direct Press.
Kennedy, J., Mendes, R., 2002. Population structure and
particle swarm performance. In Proceeding Congress
of Evolutionary Computation (CEC 2002) volume 2,
p.1671-1676.
Alatas, B., Akin, E., Ozer B., 2009. Chaos embedded
particle swarm optimization algorithms. In Chaos,
Solitons and Fractals volume 40, p.1715-1734.
Science Direct Press.
Coelho, LdS., 2008. A quantum particle swarm optimizer
with chaotic mutation operator. In Chaos, Solitons and
Fractals volume 37(5), p.1409-1418. Science Direct
Press.
AFlexibleParticleSwarmOptimizationbasedonGlobalBestandGlobalWorstInformation
261

Shi, Y., Eberhart, R.C., 2001. Fuzzy adaptive particle
swarm optimization. In Proceedings of the 2001
Congress on Evolutionary Computation, volume 1,
p.101-106.
Griewangk, A.O., 1981. Generalized descent of global
optimization. In Journal of Optimization Theory and
Applications, volume 34, p.11-39.
Rastrigin, L.A., 1974. External control systems. In
Theoretical Foundations of Engineering Cybernetics
Series, Moscow, Russian, Nauka.
De Jong, K., 1975. An analysis of the behaviour of a class
of genetic adaptive systems. PhD thesis in University
of Michigan.
D. H. Ackley., 1987. A connectionist machine for genetic
hillclimbing. Boston: Kluwer Academic Publishers.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
262
