Quantiﬁed Epistemic and Probabilistic ATL

Henning Schnoor

Institut f¨ur Informatik, Christian-Albrechts-Universit¨at zu Kiel, 24098 Kiel, Germany

Keywords:

ATL, Multi-agent systems, Epistemic Logic.

Abstract:

We introduce QAPI (quantiﬁed ATL with probabilism and incomplete information), which extends epistemic

and probabilistic ATL with a ﬂexible mechanism to reason about strategies in the object language, allowing

very ﬂexible treatment of the behavior of the “counter-coalition”. QAPI can express complex strategic proper-

ties such as equilibria. We show how related logics can be expressed in QAPI, provide bisimulation relations,

and study the issues arising from the interplay between quantiﬁers and both epistemic and temporal operators.

1 INTRODUCTION

ATL (Alternating-time temporal logic) (Alur et al.,

2002) is a logic to reason about strategic properties of

games. Its strategy operator hhAiiϕ expresses “there

is a strategy for coalition A to achieve ϕ.” We in-

troduce QAPI (quantiﬁed ATL with probabilism and

incomplete information), a powerful epistemic and

probabilistic extension of ATL with quantiﬁcation of

and explicit reasoning about strategies. QAPI’s key

features are:

• Strategy Variables allow explicit reasoning about

strategies in the object language,

• A generalized Strategy Operator ﬂexibly binds

the behavior of some coalitions to strategies,

while the remaining players exhibit standard ATL

“worst-case” behavior,

• Quantiﬁcation of strategy variables expresses de-

pendence between strategies.

Existential quantiﬁcation of strategies already ap-

pears as part of the hh.ii-operator of ATL, however

QAPI makes this more explicit and allows separat-

ing the quantiﬁcation of a strategy and the reasoning

about it in the formulas. To this end, the logic can

reason directly about the effect of a coalition follow-

ing a strategy and express statements as “if coalition

A follows strategy s, then ϕ is true.”

QAPI properly includes e.g., ATL

∗

, strategy

logic (Chatterjee et al., 2007), ATLES (Walther et al.,

2007), (M)IATL (

Agotnes et al., 2007), ATEL-R

∗

and

ATOL (Jamroga and van der Hoek, 2004). QAPI can

reason about equilibria and express that a coalition

knows a strategy to be successful. This requirement is

often useful, and is e.g., hard-coded into the strategy

deﬁnition in (Schobbens, 2004). In addition, QAPI

features probabilistic reasoning, i.e., can express that

events occur with a certain probability bound.

We illustrate QAPI’s advantages with an impor-

tant example. When evaluating hhAiiϕ in ATL, the

behavior of players not in A (we denote this “counter-

coalition” with A) is universally quantiﬁed: A must

succeed for every possible behavior of A. Hence A

has a strategy for ϕ only if such a strategy works even

in the worst-case setting where

•

A’s only goal is to stop A from reaching the goal,

• the players in A know A’s goal,

• A’s actions may depend on unknown information.

These issues are particularly relevant when play-

ers have incomplete information about the game.

Variants of ATL for this case were suggested in

e.g., (Jamroga, 2004; Schobbens, 2004; Jamroga and

van der Hoek, 2004; Herzig and Troquard, 2006;

Schnoor, 2010b). These logics restrict agents to

strategies that can be implemented with the available

information, but still require them to be successful

for every possible behavior of the counter-coalition.

Hence the above limitations still apply—for example,

“A can achieve ϕ against every strategy of A that uses

only information available to A” cannot be expressed.

QAPI’s direct reasoning about strategies provides

a ﬂexible way to specify the behavior of all play-

ers, and in particular addresses the above-mentioned

shortcomings with a ﬁne-grained speciﬁcation of the

behavior of the “counter-coalition” A. For example,

the following behaviors of A can be speciﬁed:

•

A continues a strategy for their own goal—i.e., A

Schnoor H..

Quantiﬁed Epistemic and Probabilistic ATL.

DOI: 10.5220/0004189300140023

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 14-23

ISBN: 978-989-8565-39-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

is unaware of (or not interested in) what A does,

• A follows a strategy tailor-made to counteract the

goal ϕ, but that can be implemented with informa-

tion available to A—here A reacts to A with “real-

istic” capabilities, i.e., strategies based on infor-

mation actually available to A,

• A plays an arbitrary sequence of actions, which

does not have to correspond to an implementable

strategy—this is the pessimistic view of the logics

mentioned above: A must be successful against

every possible behavior of the players in A.

As we will show, detailed reasoning about the

counter-coalition is only one advantage of QAPI. Our

results are as follows:

1. We prove that QAPI has a natural notion of bisim-

ulation which is more widely applicable than the

one in (Schnoor, 2010b), even though QAPI is

considerably more expressive. In particular, our

deﬁnition can establish strategic and epistemic

equivalence between ﬁnite and inﬁnite structures.

2. We discuss the effects of combining quantiﬁca-

tion, epistemic, and temporal operators in detail.

The combination of these operators can lead to

unnatural situations, which motivate the restric-

tion of QAPI to inﬁx quantiﬁcation.

3. We prove complexity and decidability results for

model checking QAPI. In the memoryless case

QAPI’s added expressiveness compared to ATL

∗

comes without signiﬁcant cost: The complexity

ranges from PSPACE to 3EXPTIME for games

that are deterministic or probabilistic. Hence the

deterministic case matches the known PSPACE-

completeness for ATL

∗

with memoryless strate-

gies (Schobbens, 2004). As expected, the prob-

lem is undecidable in the perfect-recall case.

Related Work. We only mention the most closely

related work (in addition to the papers mentioned

above) from the rich literature. QAPI is an exten-

sion of the ATL

∗

-semantics introduced in (Schnoor,

2010b), and utilizes the notion of a strategy choice

introduced there. In this paper, we extend the seman-

tics and the results of (Schnoor, 2010b) by the use of

strategy variables, quantiﬁcation, and explicit strategy

assignment, which lead to a much richer language.

In particular, the semantics in (Schnoor, 2010b) does

not handle negation of the strategy operator in a sat-

isfactory way in the incomplete-information setting.

Further, our notion of a bisimulation is much more

general than the one suggested in (Schnoor, 2010b).

QAPI’s approach of allowing ﬁrst-order like quan-

tiﬁcation of strategies is very similar to the treat-

ment of strategies in strategy logic (Chatterjee et al.,

2007). However, the combination of epistemic as-

pects and quantiﬁcation reveals some surprising sub-

tleties, which we discuss in Section 4, and to the best

of our knowledge, there are no results on bisimula-

tions for strategy logic.

Relaxations of ATL’s universal quantiﬁcation

over the counter-coalition’s behavior were studied

in (

Agotnes et al., 2007; Walther et al., 2007) for

the complete-information case. In (Schnoor, 2012),

QAPI is used to specify strategic and epistemic prop-

erties of cryptographic protocols, the bisimulation re-

sults from the present paper are used to obtain a pro-

tocol veriﬁcation algorithm.

All proofs can be found in the technical re-

port (Schnoor, 2010a).

2 Syntax and Semantics of QAPI

2.1 Concurrent Game Structures

We use the deﬁnition of concurrent game struc-

tures from (Schnoor, 2010b), which extends the

one from (Alur et al., 2002) with probabilistic (see

also (Chen and Lu, 2007)) and epistemic aspects (see

also (Jamroga and van der Hoek, 2004)):

Deﬁnition 1. A concurrent game structure (CGS) is a

tuple C = (Σ, Q, P, π, ∆,δ, eq), where

• Σ and P areﬁnite sets of players and propositional

variables, Q is a (ﬁnite or inﬁnite) set of states,

• π: P → 2

is a propositional assignment,

• ∆ is a move function such that ∆(q, a) is the set

of moves available at state q ∈ Q to player a ∈ Σ.

For A ⊆ Σ and q ∈ Q, an (A, q)-move is a function

c such that c(a) ∈ ∆(q, a) for all a ∈ A.

• δ is a probabilistic transition function which for

each state q and (Σ, q)-move c, returns a discrete

probability distribution δ(q, c) on Q (the state ob-

tained when in q, all players perform their move

as speciﬁed by c),

• eq is an information function eq : {1, . .. , n} ×

Σ → P (Q× Q), where n ∈ N and for each i ∈

{1, . .. , n} and a ∈ Σ, eq(i, a) is an equivalence

relation on Q. We also call each i ∈ {1, . . . , n} a

degree of information.

Moves are merely “names for actions” and only

havemeaning in combination with the transition func-

tion δ. A subset A ⊆ Σ is a coalition of C . We

leave out “of C ” when C is clear from the context,

omit set brackets for singletons, etc. The coalition

Σ\ A is denoted with A. We write Pr(δ(q, c) = q

′

) for

A probability distribution Pr on Q is discrete, if there is

a countable set Q

′

⊆ Q such that

∑

q∈Q

′ Pr(q) = 1.

QuantifiedEpistemicandProbabilisticATL

(δ(q, c)) (q

′

), i.e., consider δ(q, c) as a random vari-

able on Q. The function eq expresses incomplete in-

formation: It speciﬁes pairs of states that a player

cannot distinguish. By specifying several relations

eq(1, a), . . . , eq(n, a) for each player, we can specify

how much information a player may use to reach a

certain goal. This is useful e.g., in security deﬁni-

tions (Cortier et al., 2007; Schnoor, 2012).

C is deterministic if all distributions δ(q, c) assign

1 to one state and 0 to all others, C has complete in-

formation if eq(i, a) is always the equality relation.

2.2 Strategies, Strategy Choices,

and Formulas

The core operator of QAPI is the strategy operator:

hhA : S

, B : S

≥α

ϕ expresses “if coalition A fol-

lows S

and B follows S

, where both coalitions base

their decisions only on information available to them

in information degree i, the run of the game satisﬁes

ϕ with probability ≥ α, no matter what players from

A∪ B do.” Here, S

and S

are variables for strat-

egy choices which generalize strategies (see below).

While similar to the ATL-operator hh.ii, the strategy

operator is much more powerful: It allows to ﬂexibly

ﬁnd a strategy to a coalition. This allows, for exam-

ple, to model that a coalition commits to a strategy (in

ATL

∗

, a strategy is revoked when the hh.ii-operator is

nested) and much more (see examples below).

Deﬁnition 2. Let C be a CGS with n degrees of in-

formation. Then the set of strategy formulas for C is

deﬁned as follows:

• A propositional variable of C is a state formula,

• conjunctions and negations of state (path) formu-

las are state (path) formulas,

• every state formula is a path formula,

• if A

, . .., A

are coalitions, 1 ≤ i ≤ n, 0 ≤ α ≤

1, and ◭ is one of ≤, <, >, ≥, and ψ is a path

formula, and S

is an A

-strategy choice variable

for each i, then hhA

: S

, . . . , A

: S

◭α

ψ is a

state formula,

• if A is a coalition, 1 ≤ i ≤ n, ψ is a state formula,

and k ∈ {D, E,C} then K

A,i

ψ is a state formula,

• If ϕ

and ϕ

are path formulas, then Xϕ

, Pϕ

−1

, and ϕ

Uϕ

are path formulas.

The values D, E, and C indicate different notions

of knowledge, namely distributed knowledge, every-

body knows, and common knowledge. We use stan-

dard abbreviations like ϕ ∨ ψ = ¬(¬ϕ ∧ ¬ψ), ♦ϕ =

true Uϕ, and ϕ = ¬♦¬ϕ. A hh.ii-formula is one

whose outmost operator is the strategy operator. In

a CGS with only one degree of information, we omit

the i subscript of the strategy operator; in a determin-

b:0

a:0

a:1

b:1

a:1

a:0

Figure 1: Strategy choices.

istic CGS we omit the probability bound ◭ α (and

understand it to be read as ≥ 1). Quantiﬁed strategy

formulas are strategy formulas in which the appearing

strategy choice variables are quantiﬁed:

Deﬁnition 3. Let C be a CGS, let ϕ be a strategy

formula for C such that every strategy choice variable

appearing in ϕ is one of S

, ..., S

. Then

∀S

∃S

∀S

. . . ∃S

is a quantiﬁed strategy formula for C .

Requiring a strict ∀∃. . . -alternation is without loss

of generality and can be obtained via dummy vari-

ables. On the other hand, allowing quantiﬁcation only

in the preﬁx is a deliberate restriction of QAPI, the

reasons for which we discuss in detail in Section 4.

Deﬁnition 4. For a player a, an a-strategy in a CGS

C = (Σ, Q, P, π, ∆, δ, eq) is a function s

with s

(q) ∈

∆(q, a) for each q ∈ Q. For an information degree i,

is i-uniform if q

∼

(a)

implies s

) = s

For A ⊆ Σ, an A-strategy is a family (s

)

a∈A

, where

each s

is an a-strategy.

Our strategies are memoryless: A move only de-

pends on the current state, not on the history of the

game. With incomplete information, the question

how players can identify suitable strategies is relevant.

Consider the CGS in Figure 1. The players are a and

b, the game starts in q

. The ﬁrst move by b controls

whether the next state is q

or q

. For x ∈ {0, 1}, q

is always followed by q

. In q

, the move 0 leads to

a state satisfying ok iff x = 0; move 1 is successful iff

x = 1. Player a cannot distinguish q

and q

. We ask

whether he has a strategy leading to ok that is suc-

cessful started in both q

and q

. If a can only use

strategies, he must play the same move in q

and in

, and thus fails in one of them. However, if a can

decide on a strategy and remember this decision, the

player can choose in q

) a strategy playing 0 (1)

in every state, and be successful.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

Strategy choices (Schnoor, 2010b) formalize how

a player chooses a strategy, and distinguish between

states where a strategy is identiﬁed and where it is ex-

ecuted: In state q

or q

, player a uses his information

to choose the strategy that he follows from then on.

When using only strategies, the knowledge has to be

present at the time of performing a move. Hence strat-

egy choices give players additional capabilities over

the pure memoryless setting, by allowing to remem-

ber decisions. In contrast to the perfect recall case,

where players remember the entire run of a game,

there is no signiﬁcant computational price, whereas

perfect recall makes the model checking problem un-

decidable (cp. Section 6).

Deﬁnition 5. A strategy choice for a coalition A in a

CGS C = (Σ, Q, P, π, ∆, δ, eq) is a function S such that

for each a ∈ A, q ∈ Q, each hh.ii

-formula ϕ, S(a, q, ϕ)

is an i-uniform a-strategy in C , and if q

∼

(a)

then S(a, q

, ϕ) = S(a, q

, ϕ).

In the deﬁnition of a strategy choice, syntax and

semantics meet, since one input to a strategy choice

is the goal a coalition is supposed to achieve—such a

goal is best speciﬁed with a formula. The formula also

speciﬁes the coalition working together to achieve the

goal. For a coalition A, and a strategy choice S for A,

the strategy chosen for A by S in a state q to reach the

goal ϕ is the A-strategy (s

)

a∈A

with s

= S(a, q, ϕ)

for each a. We denote this strategy with S(A, q, ϕ).

Strategy choices model the decision of a single player

to use a certain strategy. For coalitions, they model

strategies agreed upon before the game for possible

goals. This allows their members to predict the each

other’s behavior without in-game communication. As

mentioned above, the crucial point is that strategy

choices distinguish between states where a strategy

is identiﬁed and where it is executed: In state q

or q

of the above example, player a uses his information to

choose a strategy which he then follows. When using

only strategies, the knowledge has to be present at the

time of playing a move. A strategy choice hence al-

lows players to “remember” previous decisions. For

coalitions, it models prior agreement helpful in e.g.,

coordination games.

The strategy operator binds the behavior of the

players in the appearing coalitions to the strategies

speciﬁed by the assigned strategy choices (see below).

The remaining players (the “counter-coalition”) are

treated as “free agents” in QAPI: Every possible be-

havior of these players is taken into account. Such a

behavior may not even follow any strategy, for exam-

ple they may perform different moves when encoun-

tering the same state twice during the game. This is

formalized as a response (cp. (Schnoor, 2010b)) to a

coalition A, which is a function r such that r(t, q) is

a (A, q)-move for each t ∈ N and each q ∈ Q. This

models an arbitrary reaction to the outcomes of an A-

strategy: In the i-th step of a game, A performs the

move r(i, q), if the current state is q.

When a coalition A follows the strategy s

, and the

behavior of A is deﬁned by the response r, the moves

of all players are ﬁxed; the game is a Markov pro-

cess. This leads to the following deﬁnition of “suc-

cess probability.” A path in a CGS C is a sequence

λ = λ[0]λ[1] . . . of states of C .

Deﬁnition 6. Let C be a CGS, let s

be an A-strategy,

let r be a response to A. For a set M of paths over C ,

and a state q ∈ Q, Pr(q → M | s

+ r) is the proba-

bility that in the Markov process resulting from C , s

and r with initial state q, the resulting path is in M.

A key feature of QAPI is the ﬂexible binding of

strategies to coalitions, which is done using the strat-

egy operator. As a technical tool to resolve possi-

ble ambiguities, we introduce a “join” operation on

strategy choices: If the coalitions A

, ..., A

strategy choices S

, ..., S

, the resulting “joint strat-

egy choice” for A

∪ · ·· ∪ A

is S

◦ ·· · ◦ S

. This is a

“union” of the S

with a tie-breaking rule for players

appearing in several of the coalitions: These always

follow the “left-most” applicable strategy choice. We

deﬁne the (associative) operator ◦ as follows:

◦ S

(a, q, ϕ) =

(

(a, q, ϕ), if a ∈ A

\ A

This deﬁnition ensures that if a coalition A

∪·· ·∪

is instructed to follow the strategy choice S

◦ ··· ◦

, then evenif A

∩A

0, for each agent the strategy

choice to follow is well-deﬁned.

2.3 Evaluating Formulas

In the same manner as the syntax, we also deﬁne

QAPI’s semantics in two stages: We ﬁrst handle strat-

egy formulas, where instantiations for the appearing

strategy choice variables are given. This naturally

leads to the semantics deﬁnition for quantiﬁed for-

mulas. Our semantics is very natural: Propositional

variables and operators are handled as usual, tempo-

ral operators behave as in linear-time temporal logic,

and hhA

: S

, . . . , A

: S

≥α

ψ expresses that when

coalitions A

, . .., A

follow the strategy choices S

.. ., S

with information degree i available, the for-

mula ψ is satisﬁed with probability ≥ α. The knowl-

edge operator K models group knowledge, see below.

Deﬁnition 7. Let C = (Σ, Q, P, π, ∆, δ, eq) be a CGS,

let

−→

S = (S

, ..., S

) be a sequence of strategy choices

QuantifiedEpistemicandProbabilisticATL

instantiating

the strategy choice variables S

, ...,

. Let ϕ be a state formula, let ψ

, ψ

be path for-

mulas, let λ be a path over Q, let t ∈ N. We deﬁne

• C ,

−→

S , q |= p iff q ∈ π(p) for p ∈ P,

• conjunction and negation are handled as usual,

• (λ, t),

−→

S |= ϕ iff C ,

−→

S , λ[t] |= ϕ,

• (λ, t),

−→

S |= Xψ

iff (λ,t + 1),

−→

S |= ψ

• (λ, t),

−→

S |= Pψ

iff there is some t

′

≤ t and

(λ,t

′

−→

S |= ψ

• (λ, t),

−→

S |= X

−1

iff t ≥ 1 and (λ,t − 1),

−→

S |=

• (λ, t),

−→

S |= ψ

Uψ

iff there is some i ≥ t such that

(λ, i),

−→

S |= ψ

and (λ, j),

−→

S |= ψ

for all t ≤ j < i,

• If k ∈ {D, E,C}, then C ,

−→

S , q |= K

A,i

ϕ iff

C ,

−→

S , q

′

|= ϕ for all q

′

∈ Q with q ∼

A,i

′

(see be-

low),

• C ,

−→

S , q |= hhA

: S

, . . . , A

: S

◭α

| {z }

=:ϕ

iff for

every response r to A

∪ · ·· ∪ A

, we have



q →

λ | (λ, 0),

−→

S |= ψ

◦ ·· · ◦ S

∪ · ·· ∪ A

, q, ϕ

) + r) ◭ α.

The relations ∼

A,i

, ∼

A,i

, and ∼

A,i

referenced in

Deﬁnition 7 represent different possibilities to model

group knowledge. For a coalition A and an informa-

tion degree i, they are deﬁned as follows:

• ∼

A,i

= ∩

a∈A

eq(i, a) expresses distributed knowl-

edge: K

A,i

ϕ is true if ϕ can be deduced from the

combined knowledge of every member of A (with

respect to information degree i),

• ∼

A,i

= ∪

a∈A

eq(i, a) models everybody knows:

A,i

ϕ is true if every agent in A on his own has

enough information to deduce that ϕ holds (with

respect to information degree i),

• ∼

A,i

is the reﬂexive, transitive closure of ∼

A,i

This models common knowledge: K

A,i

ϕ expresses

that (in A, with information degree i), everybody

knows that ϕ is true, and everybody knows that

everybody knows that ϕ is true, ..., etc.

These concepts have proven useful to express the

knowledge of a group. See (Halpern and Moses,

1990) for detailed discussion.

For quantiﬁed formulas, we deﬁne:

Deﬁnition 8. Let C be a CGS, let ψ =

∀S

∃S

∀S

. . . ∃S

ϕ be a quantiﬁed strategy for-

mula for C , let q be a state of C . Then ψ is satisﬁed

I.e., if S

is an A-strategy choice variable for some

coalition A, then S

is a strategy choice for A.

in C at q, written C , q |= ψ, if for each i ∈ {2, 4, . . . n},

there is a function s

such that for all strategy choices

, S

, ..., S

n−1

, if S

is deﬁned as s

, . . . , S

i−1

)

for even i, then C , (S

, . . . , S

), q |= ϕ.

Constant strategy choices (which only depend on

the player, not on the state or the formula) are essen-

tially strategies. We introduce quantiﬁers ∃

and ∀

quantifying over constant strategy choices.

2.4 MQAPI

MQAPI (Memory-enabled QAPI), is QAPI with per-

fect recall. The semantics can be deﬁned in the

straight-forward way by encoding history in the states

of a system, see, e.g.,(Schnoor, 2010b).

3 Examples

3.1 Restricted Adversaries

The following expresses “A can achieve ϕ against ev-

ery uniform strategy of A:”

∃S

∀S



A : S

, A : S



ϕ.

This is weaker than ∃S

hhA : S

ϕ: In the latter,

A is not restricted to any strategy at all, while in the

former, A has to follow a uniform strategy.

3.2 Sub-coalitions Changing Strategy

Often, when a coalition A

′

( A changes the strategy,

they rely on A\ A

′

to continue the current one. As-

sume that A works together to reach a state where

′

( A has strategies for ϕ

and ϕ

, if players in A\A

′

continue their earlier strategy. We express this as

∃

∃S

′

hhA : S

♦( hhA

′

: S

′

, A : S

♦ϕ

∧ hhA

′

: S

′

, A : S

♦ϕ

This expresses that A uses a ﬁxed strategy and

does not change behavior depending on whether A

′

attempts to achieve ϕ

or ϕ

. In particular, A\ A

′

does

not need to know which of these goals A

′

attempts to

achieve. We use the same strategy choice for ϕ

and

to require A

′

to identify the correct strategy with

the available information.

3.3 Knowing whether a Strategy is

Successful

The following expresses “there is an A-strategy such

that there is no B-strategy such that the coalitionC can

know that its application successfully achieves ϕ:”

∃

∀

¬K

hhA : S

, B : S

ϕ.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

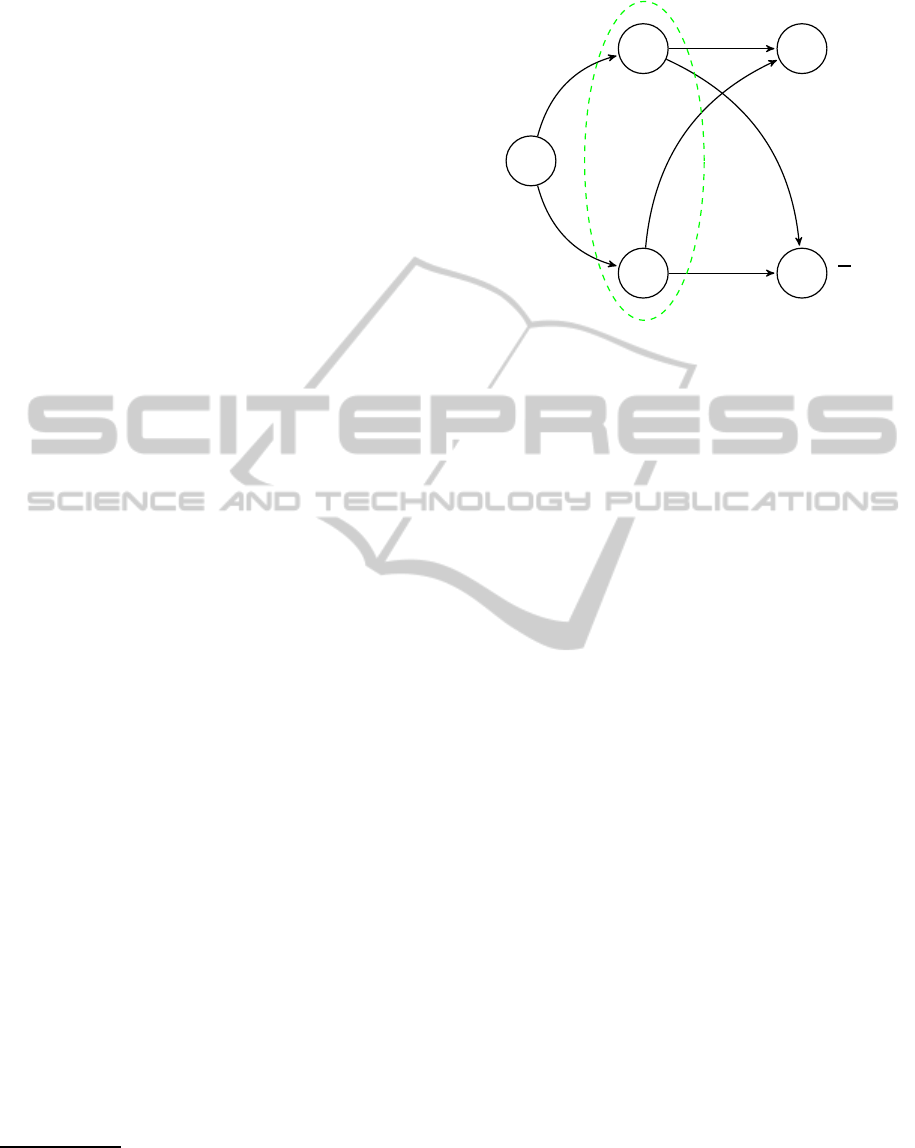
This is very different from expressing that A has

a strategy preventing ϕ, i.e., ∃S

hhA : S

¬ϕ, since

(i) There may be a successful strategy for B, but not

enough information for C to determine that it is suc-

cessful, (ii) the goal ϕ may still be reachable if B does

not follow a (uniform) strategy.

3.4 Winning Secure Equilibria (WSE)

If player a (b) has goal ϕ

(ϕ

), a WSE (Chatterjee

et al., 2006) is a pair of strategies (s

, s

) such that

both goals are achieved when a and b play s

and s

and if b plays such that ϕ

is not reached anymore, but

a still follows s

, then b’s goal ϕ

is also not satisﬁed

anymore (same for player a). QAPI can express this

as follows: Both goals are reached if (s

, s

) is played,

and neither player can reach his goal without reaching

that of the other player as well, if the latter follows the

WSE strategy.

∃

hha : S

, b : S

(ϕ

∧ ϕ

)

∧ hha : S

(ϕ

→ ϕ

)

∧ hhb : S

(ϕ

→ ϕ

3.5 Expressing ATEL-R

∗

and ATOL

ATOL (Jamroga and van der Hoek, 2004) requires

identifying strategies with the agent’s knowledge.

ATOL’s key operator is deﬁned as follows (right-hand

side in our notation)—in the following, A is the coali-

tion playing, and Γ the one identifying the strategy:

C , q |= hhAii

K (Γ)

ϕ iff there is a constant strat-

egy choice S

such that for all q

′

∈ C with

′

∼

q, we have that C , q

′

|= hhA : S

ϕ.

The above can be translated into QAPI by writing

C , q

′

|= K

hhA : S

ϕ,

where S

’s quantiﬁcation depends on the par-

ity of negation and is restricted to constant strategy

choices.

In (Jamroga and van der Hoek, 2004), it is

stated that requiring “Γ knows that A has a strategy

to achieve ϕ” is insufﬁcient to express hhAii

K (Γ)

ϕ. It

sufﬁces in QAPI since we quantify S

before the K -

operator, hence Γ knows that the ﬁxed A-strategy is

successful. ATEL-R

∗

would quantify the strategy af-

ter the K -operator in a formula like K

hhAiiϕ: A

could choose a different strategy in each state. ATEL-

∗

(ATOL with recall) can be expressed in MQAPI

analogously. The above highlights the usefulness

It is not sufﬁcient to rely on the uniformity of strat-

egy choices (the same strategy must be chosen in A-

indistinguishable states), since there must be a single strat-

egy that is successful in all Γ-indistinguishable states, and

Γ might have less information than A.

Figure 2: Inﬁx quantiﬁcation example.

of QAPI’s ability to directly reason about strategy

choices. Strategy logic (Chatterjee et al., 2007),

ATLES (Walther et al., 2007), and (M)IATL (

Agotnes

et al., 2007) can be expressed similarly.

4 QUANTIFICATION AND

EPISTEMIC/TEMPORAL

OPERATORS

We now study the interplay between quantiﬁers and

temporal or epistemic operators: Applying quantiﬁers

in the scope of epistemic or temporal operators often

leads to highly counter-intuitive behavior. This be-

havior is the reason why QAPI only allows quantiﬁ-

cation in a quantiﬁer block preﬁxing the formula. The

issues we demonstrate here are not speciﬁc to QAPI

or the concept of strategy choices, but are general ef-

fects that arise in any formalism combining the oper-

ators we discuss here with some mechanism of forc-

ing agents to “know” which strategy to apply. The

core issue is that an unrestricted ∃-quantiﬁer adds a

high degree of non-uniformity to the agent’s choices,

which is incompatible with the epistemic setting.

To demonstrate these issues, in this section, we

consider QAPI

inﬁx

, which is QAPI with arbitrary nest-

ing of quantiﬁers and other operators. The semantics

is deﬁned by applying quantiﬁcation in every state in

the obvious way. Clearly, quantiﬁcation can always

be pulled outside of the scope of propositional and

♦-operators. The remaining temporal and epistemic

operators cannot be handled so easily.

QuantifiedEpistemicandProbabilisticATL

4.1 Quantiﬁcation in the Scope of

Temporal Operators

Consider the following QAPI

inﬁx

-formula:

A∃S

hhA : S

≥1

ψ.

The quantiﬁer A abbreviates ∃S

0 : S

≥1

and

expresses quantiﬁcation over all reachable paths (es-

sentially A is CTL’s A-operator). The formula ex-

presses that in all reachable states, there is a strategy

choice for A that accomplishes ψ. There are no uni-

formity or epistemic constraints on the ∃-quantiﬁer:

Even in states that look identical for all members of A,

completely different strategy choices can be applied.

This is problematic in an epistemic setting: Consider

the CGS with two players a and b in Figure 2. We

only indicate the moves of player a. The game is turn-

based, where it is b’s turn in the state q

and a’s turn

in the remaining states. The ﬁrst action of b chooses

whether the next state is q

or q

, these two states are

indistinguishable for a. In q

, player a must play 0 to

reach a state where p holds, in state q

, a must play 1

to achieve this. Now consider the following formula

(we consider the coalition A = {a}):

AX∃S

hhA : S

≥1

This formula is true in q

: In both possible follow-

up states, there is a strategy choice that allows player

a to enforce that p is true in the next state: In q

we choose a strategy choice S

that for every possi-

ble goal and in every state always plays the move 0

(1). Individually, these strategy choices satisfy every

imaginable uniformity condition, since they ﬁx one

move forever. However, intuitively in q

, player a

cannot achieve Xp, since a cannot identify the cor-

rect strategy choice to apply. This shows that having

an existential quantiﬁer in the scope of a temporal op-

erator yields counter-intuitive results.

A natural way to address this problem is to re-

strict quantiﬁcation to be “uniform” and demand that

the quantiﬁer chooses the same strategy choice in the

states indistinguishable for A. We can express this

in QAPI

inﬁx

by requiring that the strategy choice “re-

turned” by the quantiﬁer is successful in all indistin-

guishable states—in other words, requiring A to know

that the strategy choice is successful. In this case, the

same strategy choice can be used in all indistinguish-

able states as intended. In the above example, we

therefore would consider the following formula (for

singleton-coalitions, all notions of knowledge coin-

cide, we use common knowledge in the example):

AX∃S

A,1

hhA : S

≥1

If we follow the above suggestion and always

combine existential quantiﬁcation with requiring the

knowledge that the introduced strategy choice accom-

plishes its goal, the behavior is much more natural—

however, as we now demonstrate, these are exactly

the cases which already can be expressed in QAPI.

To do this, we need to decide on a suitable no-

tion of group knowledge to apply in formulas of the

above structure. If we use distributed knowledge, we

essentially allow coordination inside the coalition A

as part of the existential quantiﬁer. This is similar to

the behavior of ATL/ATL

∗

, where the hh.ii-operator

also allows coordination. Hence distributed knowl-

edge does not achieve the desired effect. However,

everyone knows and common knowledge do not suf-

fer from these issues: In both cases, each agent on

his own can determine whether the current strategy

“works.” We now show that this intuition is supported

by formal arguments: In the case of everyone knows

or common knowledge, the existential quantiﬁer can

indeed be exchanged with the  operator, the same

does not hold for distributed knowledge.

Proposition 9. Let ϕ be a formula in which the vari-

able S

does not appear, and which does not use past-

time operators, and let k ∈ {E,C}. Then

∃S

A,i

hhA : S

≥α

ϕ ≡ ∃S

K

A,i

hhA : S

≥α

ϕ.

We require that ϕ does not contain S

, since the

idea of the above discussion is the direct coupling

of the existential quantiﬁcation of S

and the group

knowledge about the effects of its application. Re-

quiring that ϕ does not have past-time operators is

clearly crucial for memoryless strategies: If ϕ, e.g.,

requires to play a speciﬁc move if and only if that

move has been played previously, then the strategy

choice clearly must depend on the history and the

above equivalence does not hold. Proposition 9 does

not hold for distributed knowledge instead:

Example 10. Consider a CGS C with players a and

b and two Boolean variables x and y, where player a

(b) only sees the value of variable x (y) and the val-

ues of the variables change randomly in every tran-

sition. Each player always has the moves 0 and 1

available. Consider the coalition A = {a, b} and the

formula ϕ expressing “a moves according to y and b

moves according to x”

Since the distributed knowl-

edge of A allows to identify the values of both x

and y, in each state there is a strategy choice achiev-

ing ϕ, however clearly there is no single strategy

choice which works in all states. Hence, the formula

∃S

A,1

hhA : S

≥1

ϕ is always true in C , while

∃S

K

A,1

hhA : S

≥1

ϕ is always false.

To express this as a variable, the CGS needs to record

the last move of each player in the state in the obvious way.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

Proposition 9 can be generalized in several di-

rections. For ease of presentation we only present

the above simple form of Proposition 9 which sup-

ports the main argument of this section: “Intuitively

sensible” applications of quantiﬁcations inside -

operators can be eliminated.

4.2 Quantiﬁcation in the Scope

of Epistemic Operators

We now show that quantiﬁcation in the scope of epis-

temic operators leads to similar issues as the case of

temporal operators considered above. We again con-

sider the CGS in Figure 2. In q

, the formula

AXK

A,1

∃S

hhA : S

≥1

is true: Agent a (who alone forms the coalition A)

knows that there is a successful strategy choice, since

there is one in both q

and in q

. However, as seen

above, he does not know this strategy choice.

We now present a similar result to Proposition 9,

for quantiﬁcation in the scope of epistemic operators,

and identify cases in which these operators commute.

For this, we exhibit a “maximal” class of formulas for

which knowledge and quantiﬁcation can always be

exchanged. When discussing whether quantiﬁcation

of a variable S

commutes with an operator (epistemic

or otherwise), clearly we are only interested in formu-

las in which the variable S

actually plays a non-trivial

role. To formalize this, we extend the concept of a

“relevant” variable which is well-known in proposi-

tional logic, to the class of strategy variables:

Deﬁnition 11. Let ϕ be a formula with free strat-

egy variables among {S

, . . . , S

}. We say that

the variable S

is relevant for ϕ if there exists

a CGS C , a state q of C , and strategy choices

, . . . , S

, S

′

such that C , (S

, . . . , S

), q |= ϕ and

C , (S

, . . . , S

i−1

, S

′

, S

i+1

, . . . , S

), q 6|= ϕ.

This means that there exists a situation where it

matters which strategy choice is used to instantiate the

variable S

. Examples for an irrelevant variable S

are

hhA : S

≥1

(♦x∨ ¬x) or hhA : S

≥0

♦x.

Deﬁnition 12. For a coalition A and a degree of in-

formation i, k ∈ {D, E,C}, a formula ϕ is k-i-simple

in S

, if one of the following conditions is true:

• S

is an irrelevant variable of ϕ, or

• ϕ is equivalent to a formula of the form K

A,i

ψ.

Formulas that are k-i-simple give a “natural” se-

mantics when preﬁxed with an existential quantiﬁer,

since in the same way as there, the non-uniformity

of the existential quantiﬁer is reduced using the epis-

temic operator. We now show that in these cases, inﬁx

quantiﬁcation again is not necessary, as here, the ex-

istential and the epistemic operators commute:

Lemma 13. If ϕ is k-i-simple and has a single free

strategy variable, then for all CGS C and states q,

C , q |= K

A,i

∃s

ϕ if and only if C , q |= ∃s

A,i

ϕ.

This class of formulas is maximal—as soon as we

have a formula that depends on the variables S

and

of which A’s knowledge does not sufﬁce to determine

the truth, we cannot swap the above operators.

Proposition 14. Let ϕ be a formula such that ϕ is not

k-i-simple in S

and the coalition A is bound to S

the entire formula, then ∃S

A,i

ϕ 6≡ K

A,i

∃S

ϕ.

The prerequisite that A is bound to S

in the en-

tire formula is necessary to e.g., preclude cases where

is only used in a non-meaningful way. It is not

a strong requirement, as (with inﬁx quantiﬁcation)

usually the subformula directly succeeding the exis-

tential quantiﬁer will be the one “talking about” the

quantiﬁed strategy choice. It is possible to strengthen

Proposition 14, howeveragain the simple form here is

sufﬁces to show that in the cases where quantiﬁcation

in the scope of an epistemic operator gives a satis-

factory semantics, the quantiﬁer can be moved out of

scope of that operator, and hence QAPI sufﬁces.

4.3 Discussion

Nesting of quantiﬁcation and epistemic or temporal

operators leads to counter-intuitive behavior, since

quantiﬁcation introduces a degree of non-uniformity,

whereas a core issue in the epistemic setting is to en-

force sufﬁcient uniformity to ensure that agents have

enough knowledge to decide on the “correct” move to

play in every situation. Although we did not give a

complete characterization of the cases in which tem-

poral/epistemic operators and quantiﬁers commute

and it is notoriously difﬁcult to give a good deﬁni-

tion of a “natural” semantics, our results give strong

evidence for our claim: In the cases where inﬁx quan-

tiﬁcation leads to a natural semantics, the quantiﬁers

can be swapped with the temporal/epistemic opera-

tors, hence inﬁx quantiﬁcation is unneeded.

Another reason why QAPI only allows quantiﬁers

in the preﬁx of a formula is that in the presence of

strategy choices, inﬁx quantiﬁcation does not seem

to be particularly useful: Quantiﬁcation of strategies

that may be different in any state can be handled by

strategy choices in a way that is compatible with the

epistemic setting, since strategy choices may return

different strategies in states that are distinguishable

for an agent. On the other hand, inﬁx quantiﬁcation

of strategy choices is very unnatural: Strategy choices

QuantifiedEpistemicandProbabilisticATL

express “global behavior” of coalitions allowing prior

agreement, but during the game only rely on commu-

nication that is part of the game itself. Quantiﬁcation

inside formulas would express “prior agreement” dur-

ing the game, which defeats its purpose.

There may be interesting properties that can only

be expressed using QAPI

inﬁx

, but usuallyz QAPI is

sufﬁcient and avoids the above problems.

5 SIMULATIONS

Bisimulations relate structures in a truth-preserving

way. They allow to obtain decidability results for

game structures with inﬁnite state spaces (if a bisimi-

lar ﬁnite structure exists), or can reduce the state space

of a ﬁnite system. In (Schnoor, 2012), our bisimula-

tion results are used to obtain a model-checking al-

gorithm on an inﬁnite structure by utilizing a bisim-

ulation between this structure and a ﬁnite one. We

give the following deﬁnition, which is signiﬁcantly

less strict than the one in (Schnoor, 2010b): For ex-

ample, our deﬁnition can establish bisimulations be-

tween structures with different numbers of states (see

example below). This is not possible in the deﬁni-

tion from (Schnoor, 2010b), since there a bisimula-

tion is essentially a relation Z which is a simulation

in both directions simultaneously. Since a simulation

in the sense of (Schnoor, 2010b) is a function be-

tween state spaces, this implies that Z must contain,

for every state in one CGS, exactly one related state

in the other. Hence such a Z induces a bijection be-

tween state spaces, and is essentially an isomorphism.

The following deﬁnition is somewhat simpliﬁed to in-

crease readability, it only treats game structures that

have a single degree of information, which is there-

fore omitted here.

Deﬁnition 15. Let C

and C

be CGSs with state sets

and Q

, the same set of players, and the same set

of propositional variables. A probabilistic bisimula-

tion between C

and C

is a pair of functions (Z

, Z

)

where Z

: Q

→ Q

and Z

: Q

→ Q

such that there

are move transfer functions ∆

and ∆

such that for

{i,

i} = {1, 2} and all q

∈ Q

, q

= Z

), and all

coalitions A:

• q

and q

satisfy the same propositional variables,

• if c

is a (A, q

) move, the (A, q

)-move

(a) = ∆

(a, q

, c

(a)) for all a ∈ A satis-

ﬁes that for { j,

j} = {1, 2} and all (A, q

moves c

, there is a (A, q

)-move c

such that

for all q

′

∈ Q

, Pr



(δ(q

, c

∪ c

′

)) = q

′





δ(q

, c

∪ c

) = q

′



• if q

∼

′

, then ∆

(a, q

, c) = ∆

(a, q

′

, c) for all c

• if q

∼

′

, then Z

) ∼

′

)

• if q

∼

′

, there is q

′

with Z

′

) = q

′

and q

∼

′

• Z

◦ Z

and Z

◦ Z

are idempotent.

a:1

b:1

b:0

a:1

a:2

a:3

a:4

b:1

b:0

b:1

b:0

b:1

b:0

Figure 3: Game Structures C

and C

Theorem 16. Let C

and C

be concurrent game

structures, let (Z

, Z

) be a probabilistic bisimulation

between C

and C

, let q

and q

be states of C

and

with Z

) = q

and Z

) = q

. Let ϕ be a

quantiﬁed strategy state formula. Then C

, q

|= ϕ if

and only if C

, q

|= ϕ.

Consider the games C

and C

in Figure 3. In

both, player a starts, he has a single choice in C

and 4 choices in C

. The move by b then determines

whether ok holds in the ﬁnal state. In states r

of C

and q

, q

, and q

of C

, a must play 1 to make ok

true, in state q

of C

, he must play 0. States q

and

are indistinguishable for a in C

. CGSs C

and C

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

with state sets Q

and Q

are bisimilar via (Z

, Z

where Z

: Q

→ Q

is deﬁned as follows:

• Z

) = r

• Z

) = Z

) = r

• Z

) = Z

) = r

• Z

) = Z

) = r

The move transfer function swaps moves 0 and 1

when transferring from r

to q

. Z

: Q

→ Q

maps

to q

, r

to q

, r

to q

and r

to q

, the move trans-

fer functions map all of a’s possible moves in q

the move 1, the moves of b are mapped to themselves

(note that q

is not used in this direction). It is easy to

check that (Z

, Z

) is a bisimulation.

Theorem 16 states that state related via both Z

and Z

satisfy the same formulas. This applies to

, q

), (r

, q

), (r

, q

), and (r

, q

). The example

shows a bisimulation between structures with com-

plete and incomplete information, and with different

cardinalities.

6 MODEL CHECKING

COMPLEXITY

Model checking is the problem to determine, for a

CGS C , a quantiﬁed strategy formula ϕ, and a state q,

whether C , q |= ϕ. We state the following results for

completeness, the proofs are straight-forward using

results and techniques from the literature (Alur et al.,

2002; Br´azdil et al., 2006; Chatterjee et al., 2007;

Schnoor, 2010b). We note that the model-checking

problem for MQAPI is undecidable except for restric-

tions that reduce QAPI to strategy logic.

Theorem 17. The QAPI model-checking problem is

1. PSPACE-complete for deterministic CGSs,

2. solvable in 3EXPTIME and 2EXPTIME-hard for

probabilistic structures.

REFERENCES

Agotnes, T., Goranko, V., and Jamroga, W. (2007).

Alternating-time temporal logics with irrevocable

strategies. In (Samet, 2007), pages 15–24.

Alur, R., Henzinger, T. A., and Kupferman, O. (2002).

Alternating-time temporal logic. Journal of the ACM,

49(5):672–713.

Br´azdil, T., Brozek, V., Forejt, V., and Kucera, A. (2006).

Stochastic games with branching-time winning objec-

tives. In LICS, pages 349–358. IEEE Computer Soci-

ety.

Chatterjee, K., Henzinger, T. A., and Jurdzinski, M. (2006).

Games with secure equilibria. Theor. Comput. Sci.,

365(1-2):67–82.

Chatterjee, K., Henzinger, T. A., and Piterman, N. (2007).

Strategy logic. In Caires, L. and Vasconcelos, V. T.,

editors, CONCUR, volume 4703 of Lecture Notes in

Computer Science, pages 59–73. Springer.

Chen, T. and Lu, J. (2007). Probabilistic alternating-time

temporal logic and model checking algorithm. In Lei,

J., editor, FSKD (2), pages 35–39. IEEE Computer So-

ciety.

Cortier, V., K¨usters, R., and Warinschi, B. (2007). A crypto-

graphic model for branching time security properties

- the case of contract signing protocols. In Biskup,

J. and Lopez, J., editors, ESORICS, volume 4734 of

Lecture Notes in Computer Science, pages 422–437.

Springer.

Halpern, J. Y. and Moses, Y. (1990). Knowledge and com-

mon knowledge in a distributed environment. Journal

of the ACM, 37:549–587.

Herzig, A. and Troquard, N. (2006). Knowing how to play:

uniform choices in logics of agency. In Nakashima,

H., Wellman, M. P., Weiss, G., and Stone, P., editors,

AAMAS, pages 209–216. ACM.

Jamroga, W. (2004). Some remarks on alternating tem-

poral epistemic logic. In Proceedings of Formal Ap-

proaches to Multi-Agent Systems (FAMAS 2003, pages

133–140.

Jamroga, W. and van der Hoek, W. (2004). Agents that

know how to play. Fundamenta Informaticae, 63(2-

3):185–219.

Samet, D., editor (2007). Proceedings of the 11th Confer-

ence on Theoretical Aspects of Rationality and Knowl-

edge (TARK-2007), Brussels, Belgium, June 25-27,

2007.

Schnoor, H. (2010a). Explicit strategies and quantiﬁcation

for ATL with incomplete information and probabilis-

tic games. Technical Report 1008, Institut f¨ur Infor-

matik, Christian-Albrechts-Universit¨at zu Kiel.

Schnoor, H. (2010b). Strategic planning for probabilistic

games with incomplete information. In van der Hoek,

W., Kaminka, G. A., Lesp´erance, Y., Luck, M., and

Sen, S., editors, AAMAS, pages 1057–1064. IFAA-

MAS.

Schnoor, H. (2012). Deciding epistemic and strategic prop-

erties of cryptographic protocols. In Foresti, S., Yung,

M., and Martinelli, F., editors, ESORICS, volume

7459 of Lecture Notes in Computer Science, pages

91–108. Springer.

Schobbens, P.-Y. (2004). Alternating-time logic with imper-

fect recall. Electronis Notes in Theoretical Computer

Science, 85(2):82–93.

Walther, D., van der Hoek, W., and Wooldridge, M. (2007).

Alternating-time temporal logic with explicit strate-

gies. In (Samet, 2007), pages 269–278.

QuantifiedEpistemicandProbabilisticATL