Vocal Fold Stiffness Estimates for Emotion Description in Speech

Victoria Rodellar, Daniel Palacios, Elena Bartolomé and Pedro Gómez

Grupo de Informática Aplicada al Tratamiento de Señal e Imagen, Neuromorphic Speech Processing Laboratory,

Centro de Tecnología Biomédica and Facultad de Informática, Universidad Politécnica de Madrid,

Campus de Montegancedo, s/n, 28223 Pozuelo de Alarcón, Madrid, Spain

Keywords: Glottal Source, Emotional Tremor, Phonation Parameters, Voice Production.

Abstract: The present study affords emotional differentiation in speech from the behaviour of the biomechanical

stiffness estimates in voice, regarding dispersion and cyclicality. The Glottal Cyclic Parameters are derived

from the vibrato correlates found in the Glottal Source reconstructed from the phonated parts of speech and

have been shown to be good indices to neurologic disease detection and monitoring. In this paper the

application of these parameters to the characterization of the emotional states affecting a speaker when

expressing truth opposite to when they believe not saying the truth is explored. The study is based on the

reconstruction of the vocal fold stiffness parameters and in the detection of possible deviations induced by

emotional tremor and stress from a baseline. The method is validated using results from the analysis of a

gender-balanced speaker’s database. Normative values for the different parameters estimated are given and

used in contrastive studies of some cases presented to discussion.

1 INTRODUCTION

A challenging research field is to create artificial

machines capable to react to emotions and leave the

science fiction films behind. Human affective

behaviour is multimodal and complex (Lewis et al.,

2008). Emotion expression has its reflex on the

body, gesture and speech. Speech emotion detection

has many potential applications, as video and

computer games, talking toys, text/speech

converters, language translators, speech forensics,

customer centres, etc. Speech emotion detection may

be the key point to react in a fast and efficient

manner in some situations, for instance, a phone call

to the police station to report an emergency or an

abuse, to a call centre to ask for some information or

to put a complaint, or to an urgent medical care

service asking for help, etc. The steps involved to

detect emotions are estimating the basic parameters

to characterize emotions and then find emotional

patterns related. In the areas of body and gesture

emotion expression to characterize the base neutral

state is easy and to characterize other emotional

states though the visible muscle tension changes

associating muscle action patterns to emotion states

may be straight forward. Speech production is a very

complex action influenced by a combination of

neurological, physiological, psychological, social

and cultural aspects. The emotions must be inferred

from the information contained in sound waves

produced by phonatory and articulatory neuromotor

actions. There are many characteristics that can be

parameterized from the sound signal, but there is not

an agreement among researchers nor proven

evidence about which of them clearly define or

profile emotions. This is the key point to determine a

precise specification of speech based emotional state

in natural, posed or induced vocal expressions. The

presence of vocal expression patterns in particular

emotional situations should also be taken into

consideration. Besides, oral communication in

natural language is rather imprecise, which adds

more difficulties to systematically associate

emotional states to speech. Classical literature

focuses research on the analysis of phonetic and

prosodic features of speech. Some of those

characteristics are: fundamental frequency or pitch

(F0) which represents the vibration rate of the vocal

folds or the duration of the glottal cycles, first (F1)

and second (F2) formant frequencies, and amplitude

or intensity, as the amount of vibration in a sound

pressure wave, roughly used as synonymous with

the degree of softness or loudness, volume or vocal

power, linear predition coefficientes (LPC), Mel-

Frequency Cepstral coefficents (MFCC), zero

112

Rodellar V., Palacios D., Bartolomé E. and Gómez P..

Vocal Fold Stiffness Estimates for Emotion Description in Speech.

DOI: 10.5220/0004190201120119

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 112-119

ISBN: 978-989-8565-36-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

crossing rate, duration of a sentence, speech rate,

silence duration, etc (Hasrul et al., 2012). More

recently features related with voice quality have

been also taken in consideration (Airas et al., 2006),

(Moore et al., 2008). The present approach is based

on the idea that emotional states and neurologic

diseases alter or difficult the precise action of

neuromotor activity induced by the brain and

produce correlates in voice and speech. It is known

that voice could help in monitoring the neurologic

disease (Gómez et al., 2011), and this fact could also

help in the characterization of emotional states. An

early work was that of Gamboa et al. (1997) using

distortion parameters as jitter, shimmer, and HNR to

monitor dopaminergic drug dosing in Parkinson

Disease treatment. For a review of other interesting

approaches see Tsanas et al. (2009). Through the

present paper a method to track emotional correlates

in voice is introduced. The main idea is to obtain

biomechanical marks from the glottal source as

vocal fold stiffness (on body and cover) to estimate

dispersion and cyclicality patterns (non-voluntary

tremor). Through the present paper the main

assumptions are introduced, an inverse model is

presented and estimates from a validation database

are given. Example study cases are compared

against results from the validation database.

2 VOCAL FOLD PARAMETERS

The vibration of the Vocal Folds is driven by

transglottal pressure and modulated by the

interaction with resulting glottal flow (deVries et al.,

2002). In a phonation cycle the neuromotor stimulus

of the trans and oblique cricoarytenoidal muscles

brings both Vocal Folds together producing a

closure of the Larynx. Pressure build-up forces the

Vocal Folds to come apart against viscoelastic

muscular forces. The interaction between the glottal

flow and the Vocal Folds is a fluid-structure

problem, which requires solutions in 3D and time

domain. Nevertheless for the purpose of obtaining

first-order estimates simpler models may be used

reducing the computational complexity of the

problem. In this sense the Vocal Folds may be

modelled as biomechanical second-order multiple-

mass systems as far as small signal vibration is

concerned (Berry, 2001) as the one presented in

Figure 1, explaining the response to external driving

forces (Švec et al., 2000). The behavior of such a

system show resonance peaks resulting from body-

cover mass-spring interactions (R

bl,r

, M

bl,r

, K

bl,r

, R

cl,r

, K

cl,r

, b: body, c: cover, l: left, r: right) and in-

between valleys induced by inter-elasticity K

bcl,r

Figure 1: Electromechanical equivalent of the small signal

two-mass vocal fold model (body and cover).

The estimation of the electromechanical

equivalents requires the solution of an inverse

problem given the power spectral density of the

glottal source. This signal cannot be considered a

small-signal vibration, but assuming that the

Average Acoustic Wave s

(n) (Titze, 1994) is

removed from the glottal source s

(n), the residual

(t) could be seen as a correlate of the Vocal Fold

small-signal vibration

)()()( tststs

agr





(1)

Defining its power spectral density as











dtetsS

)()(

(2)

and relating it mainly with the Vocal Fold Cover

vibration, a cost function could be introduced to

express the difference between the power spectral

density and the transfer function of the

electromechanical equivalent of the upper and lower

branches of 0, given as T(ω)









dTSL

cr



),,,()(),,,(

(3)

where μ, σ and ξ stand for the estimates of each

respective massive, viscous and elastic parameter of

the body and cover biomechanics (R

bl,r

, M

bl,r

, K

bl,r

cl,r

, M

cl,r

, K

cl,r

) Different matching functionals may

be proposed for spectral fitting in 0. For instance

assuming a single second-order functional as



















 2

)(

),,,(

ccc







(4)

relating the cover mass velocity V

with the applied

force F

in the frequency domain where Y

is a

mechanical trans-admittance, the process of

optimization would imply the simultaneous fulfilling

of the following conditions for the cover parameters

;0;0;0 











ccc

LLL



(5)

VocalFoldStiffnessEstimatesforEmotionDescriptioninSpeech

113

Solutions for these conditions may be found either

by forcing the derivatives of the functional L to zero

deriving expressions for the three fitting parameters,

or by adaptive gradient methods. The solution

adopted in the present approach is based on fitting

the glottal source power spectral density in Figure 2

(full line) by the transfer function (circles) given by

(4) against the Average Acoustic Wave (triangles,

see Gómez et al., 2005).

3 CYCLICALITY ESTIMATION

The working hypothesis would then be that

pathology-induced tremor may leave correlates in

different biomechanical parameters. Specifically, it

is hypothesized that the influence of the neurological

disease has to leave a mark in the tension ξ

on the

vocal folds as a cyclic pattern.

Figure 2: Matching the glottal source power spectral

density (thin blue line) shown against the Average

Acoustic Wave power spectral density (triangles) and the

approximation function (circles).

The burning question now is how to estimate

cyclic behaviour on the observed tension. A possible

approach could be AR modelling by adaptive

inverse filtering (Deller et al., 1993) as shown in

Figure 3. The Average Acoustic Wave may be seen

as a long-range first order vibration giving the

average movement of a single spring-mass system

with the same fundamental period. The stiffness

estimate at phonation cycle m being ξ

its AR

model would be described as

imim











(6)

where a={a

} are the model coefficients. The

estimation of these coefficients is carried out by an

adaptive lattice filter (Deller et al., 1993) defined as

an operator Φ

{·} producing an output error ε

(m)

minimized in terms of LMS on a sliding time

window W

, along the phonation cycle m, rendering

a set of sub-optimal models from a non-stationary

input series ξ

with an adaptation factor β















,,,

KcmKmKmKm





(7)

Either the pivoting coefficients c

or those of the

equivalent transversal model a

may be used as

cyclicality descriptors. Both sets of coefficients are

related by the Levinson-Durbin iteration

mkkmmkkm







aaa

(8)

where ã is the order-reversal operation on vector a

(Deller et al., 1993). In the present study pivoting

coefficients will be preferred, as they are pre-

normalized to (-1, 1), which allows easier result

contrasting. In the present case the three lowest-

order pivoting coefficients {c

, c

} will be

used as descriptors of the stiffness cyclic pattern.

Examples of the estimation of these parameters from

0.2 s of vowel /e/ are given in Figure 6 to Figure 9.

Figure 3: Cyclic parameter estimation chain. Glottal

source

(n) is derived from voiced speech s

(n). The

power spectral density of the residual

(ω) after removing

the Average Acoustic Wave is matched to obtain the fold

tension ξ

at each phonation cycle m. Results from some

hundred millisecond intervals may be used to estimate the

cyclic parameters {c

4 RESULTS AND DISCUSSION

4.1 Database Validation

The strategy followed in this study for validation

purposes assumes that a priori knowledge on the

distribution of the cyclic parameters is not available.

A more controversial hypothesis would be the

extension of this same assumption to dysphonic

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

114

speakers affected by organic pathologies with

negative neurological etiology. To create the

reference baseline a database of recordings from

normal and organic-dysphonic speakers was

recruited with the following distribution: 50 normal

males, 50 normal females, 50 organic-dysphonic

males, and 50 organic-dysphonic females. The

records consisted in sustained utterances of vowel /a/

longer than 2 s long. Glottal Source correlates were

obtained from the voice segments, and

biomechanical stiffness was used to estimate the

cyclic coefficients c

, c

and c

as explained before.

The histograms of these three parameters are given

in Figure 4 (males) and Figure 5 (females).

‐1 ‐0,9 ‐0,8 ‐0,7 ‐0,6 ‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5

Cyclic Parameter 1 (Males)

Normophonics

Dysphonics

‐1 ‐0,9 ‐0,8 ‐0,7 ‐0,6 ‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5

Cyclic Parameter 2 (Males)

Normophonics

Dysphonics

‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

Cyclic Parameter 3 (Males)

Nor mophonics

Dysphonics

Figure 4: Distributions of the first three cyclicality

parameters for male subjects.

The overlapping between the normophonic and

dysphonic distributions for males and females shows

that hypothesizing a similar behaviour for these two

distributions regarding emotion and neural

pathology neutral conditions is well founded.

‐1 ‐0,9 ‐0,8 ‐0,7 ‐0,6 ‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5

Cyclic Parameter 1 (Females)

Nor mophonics

Dysphonics

‐1 ‐0,9 ‐0,8 ‐0,7 ‐0,6 ‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5

Cyclic Parameter 2 (Females)

Nor mophonics

Dysphonics

‐0,5 ‐0,4 ‐0,3 ‐0,2 ‐0,1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

Cyclic Parameter 3 (Females)

Nor mophonics

Dysphonics

Figure 5: Distributions of the first three cyclicality

parameters for female subjects.

4.2 Study Cases

To exemplify the capabilities of this methodology to

characterize non-neutral emotional states several

phenomenological study cases are presented. These

correspond to cyclicality parameters estimated on a

male and a female speaker who are being recorded

under subtle emotional conditions. These are

aroused by asking specific opinions to the speaker

on sensitive social issues regarding economy, cost of

living, unemployment, etc. Once a first set of

statements is produced the speaker is asked to

convince the interviewer that his/her opinion is just

the opposite of the one expressed before, without

any other requirement. The first set of statements

VocalFoldStiffnessEstimatesforEmotionDescriptioninSpeech

115

shows more spontaneity, whereas the second set of

statements is produced under notorious hesitation,

and the speaker introduces more pauses and larger

number of fillers, as this second opinion has to be

somehow "fabricated". The fillers consist in the

emission of long vowels, mainly /ah/, /uh/, /eh/,

which have been found very useful for the analysis

of the stress manifested in the stiffness of the body

fold and cover. The frequency with which fillers as

/eh/ are to be found in Spanish is larger than /ah/.

Therefore the analysis is concentrated on /eh/ rather

than /ah/. The database has been validated with /ah/,

but as the articulation patterns are removed during

vocal tract inversion both types of emissions may be

considered compatible as far as stiffness estimates

are concerned. Therefore the four study cases

presented shown comparisons of emissions of /eh/ as

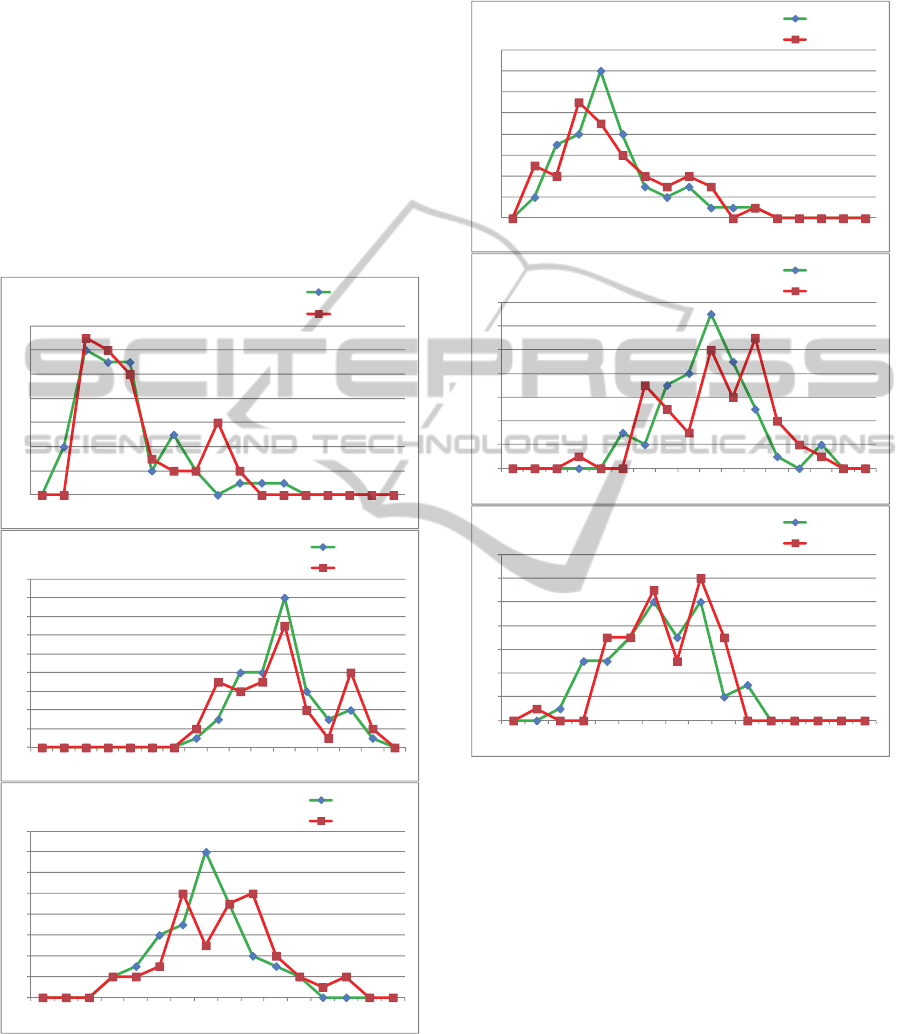
given in figure 6 to Figure 9. They show the

analysis of a filler /eh/ from a male and female

speaker expressing spontaneous (MSS/FSS) and

opposite-to-spontaneous (MSO/FSO) opinions. The

evolution of vocal fold body stiffness in a 0.2 s

segment (red) and the same trace low pass filtered

and unbiased (blue) are given in the left column

(top). The statistical distribution box plot of the

unbiased vocal fold body stiffness is given in the

upper right. The evolution of the three cyclicality

estimates and their statistical distributions (medians

given in figures) are in the bottom left and right

templates, respectively.

The results given in the above four figures are

also summarized in Table 1. Several facts have to be

pinpointed from the figures corresponding to MSS

and MSO. The first one is that the body stiffness

seems to be less stable and shows a wider decay in

the spontaneous utterance in the male case. This can

also be confirmed by the standard deviation for this

parameter (σKb) in Table 1. This could be

associated with a less stressed phonation condition

when the speaker is spontaneous than when has to

"fabricate" a fictitious opinion, although the mean

tension of the vocal fold (μKb) remains almost the

same. The situation is not the same in the female

case studied as far as the body stiffness is concerned,

but if the cover stiffness is examined the larger

dispersion in σKc for MSS and FSS (spontaneous)

compared with the non-spontaneous MSO and FSO

is evident for both genders. The comparison of the

cyclic parameters in the spontaneous vs non-

spontaneous is that the first one (c1) shows a decay

towards -1 that is almost twice larger in the female (-

0.8 to -0.92) than in the male case (-0.8 to -0.86),

whereas c2 moves down as well in both cases (-0.01

to -0.18 for the male speaker, and 0.1 to -0.2 for the

female speaker). The third cyclicality parameter

does not show such a clear orientation, although is

supposed to be larger in both cases for the non-

spontaneous behaviour. It is interesting to comment

that the first cyclicality coefficient tendency towards

the lower limit is also present in speakers affected by

certain neurological diseases when tremor is present

(spasmodic dysphonia, Parkinson Disease, see

Gomez et al. 2011). The fact that cover stiffness

dispersion shows to be larger in spontaneous

phonation could be interpreted as that the speaker

leaves the vocal folds go looser under less stressed

conditions (spontaneous phonation) than under self-

controlled and more stressed a situation (non-

spontaneous phonation). A second observation is

that the average stiffness is not very much altered

from one situation to the other, but its dispersion is

clearly different (lower under non-spontaneous

conditions), and that the first two cyclicality

parameters show also a clear difference between

both conditions. The reasons for these variations to

be larger in the female case need not be necessarily

related to gender, but possibly to the specific

idiopathic behaviour of the speaker, although this

issue is worth to be assessed with a larger database

of spontaneous vs. non-spontaneous utterances

produced by both gender speakers.

5 CONCLUSIONS

A first observation is that the chain model from

voice to vocal fold tension estimation and to the

cyclicality parameters of vocal fold stiffness

normophonic and organic pathology-affected

speakers on neutral emotional conditions seems to

behave accordingly with the main assumptions

formulated. The statistical distributions for male and

female speakers not affected by neurological

diseases show certain coherence, and are defined

enough to allow contrastive studies to be carried out.

From this observation it may be concluded also

that the estimation methodology both for the glottal

source, its biomechanical correlates, and the cyclical

parameters seems to be robust enough to extend the

study to larger databases of speakers showing

emotionally distorted phonation. Coming to the

detection of emotions in voice it seems that the

contrastive study on spontaneous to non-

spontaneous speech may offer differential marks in

the dispersion of body, and specially cover fold

stiffness, and in the cyclicality parameters derived

from body stiffness. Obviously the study is far from

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

116

Table 1: Vocal Fold Stiffness and Cyclicality Coefficients. From left to right: Start and End points of fillers, means of body

and cover stiffness, standard deviations of body and cover stiffness, and three cyclicity parameters.

Segment Start (s) End (s) μKb (g.s

-1

) μKc (g.s

-1

) σKb σKc c1 c2 c3

MSS 15.21 15.41 10,916 8,230 941 1529 -0.80 -0.01 0.16

MSO 3.40 3.60 10,599 7,267 213 321 -0.86 -0.18 0.18

FSS 12.40 12.60 17,661 9,432 621 2096 -0.80 0.10 0.01

FSO 7.80 8.00 17,473 9,917 758 997 -0.92 -0.20 0.22

Figure 6: Analysis of a filler /eh/ from a male speaker expressing spontaneous opinion (MSS).

Figure 7: Analysis of a filler /eh/ from a male speaker expressing opposite-to-spontaneous opinion (MSO).

VocalFoldStiffnessEstimatesforEmotionDescriptioninSpeech

117

Figure 8: Analysis of a filler /eh/ from a female speaker, spontaneous opinion (FSS).

Figure 9: Analysis of a filler /eh/ from a female speaker, non-spontaneous opinion (FSO).

being complete and needs to be extended from this

type of emotion detection to other scenarios where a

wider set of emotions is to be considered. These

results foresee the applicability of the methodology

to open new ways for emotional detection and

monitoring.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

118

REFERENCES

Airas, M., Alku, P., 2006. Emotions in vowel segments of

continous speech: analysis of glottal flow using the

normalized amplitude quotient. Phonetica, Vol. 63,

pp. 26-46.

Berry, D. A., 2001. Mechanisms of modal and non-modal

phonation.

J. Phonetics, Vol. 29, pp. 431-450.

Deller, J. R., Proakis, J. G., and Hansen, J. H. L., 1993.

Discrete-Time Processing of Speech Signals,

Macmillan Pub. Co., Englewood Cliffs, NJ.

deVries, M. P., Schutte, H. K., Veldman, A. E. P.,

Verkerke, G. J., 2002. Glottal flow through a two-

mass model: Comparison of Navier-Stokes solutions

with simplified models,

J. Acoust. Soc. Amer., Vol.

111, pp. 1847-1853.

Gamboa, J., Jiménez, F. J., Nieto, A., Montojo, J., Ortí,

M., Molina, J. A., et al., 1997. Acoustic Voice

Analysis in Patients with Parkinson’s Disease Treated

with Dopaminergic Drugs,

J. Voice, Vol. 11, pp. 314-

320.

Gómez, P., Fernández, R., Rodellar, V., Nieto, V.,

Álvarez, A., Mazaira, L. M., Martínez, R, Godino, J.

I., 2009. Glottal Source Biometrical Signature for

Voice Pathology Detection”,

Speech Comm., Vol. 51,

pp. 759-781.

Gómez, P., Martínez, R., Díaz, F., Lázaro, C., Álvarez, A.,

Rodellar, V., Nieto, V., 2005. Voice Pathology

Detection by Vocal Cord Biomechanical Parameter

Estimation,

Lecture Notes on Artificial Intelligence

3817, Springer, Berlin, pp. 242-256.

Gómez, P., Rodellar, V., Nieto, V., Muñoz, C., Mazaira,

L. M., Ramírez, C., Fernández, M., Toribio, E., 2011.

Neurological Disease Detection and Monitoring from

Voice Production.

Lecture Notes on Artificial

Intelligence,

7015, pp. 1-8.

Hasrul, M. N., Hariharan, M., Yaacob, S., 2012. Human

Affective (Emotion) Behaviour Analysis using Speech

Signals: A Review.

2012 International Conference on

Biomedical Engineering (ICoBE),

pp. 217-222.

Lewis, M., Haviland-Jones, J. M., Feldman-Barret, L.,

Eds, 2008.

Handbook of emotions. Guildford Press.

Moore, E., Clements, M. A., Peifer, J. W. Weiser, L.,

2008. Critical Analysis of the Impact of Glottal

Features in the Classification of Clinical Depression in

Speech. IEEE Trans. on Biomedical Engineering, Vol.

55, pp. 96-107.

Švec JC, Horáček J, Šram F, Veselý J., 2000. Resonance

properties of the vocal folds: In vivo laryngoscopic

investigation of the externally excited laryngeal

vibrations,

J. Acoust. Soc. Am., Vol. 108 (4), 1397-

1407.

Titze, I. R., 1994. Summary Statement, Workshop on

Acoustic Voice Analysis

, National Center for Voice

and Speech (1994).

Tsanas, A., Little, M. A., McSharry, P. E., Ramig, L. O.,

2009. Accurate telemonitoring of Parkinson's disease

progression by non-invasive speech tests, IEEE Trans.

Biomed. Eng.

Vol. 57, 2009, pp. 884-893.

VocalFoldStiffnessEstimatesforEmotionDescriptioninSpeech

119