Performance of Beta-Binomial SGoF Multitesting Method for

Dependent Gene Expression Levels

A Simulation Study

Irene Castro-Conde

and Jacobo de Uña-Álvarez

1,2

SiDOR Research Group, University of Vigo, Facultad de Económicas, 36310 Vigo, Spain

Department of Statistics and OR, University of Vigo, Facultad de Económicas, 36310 Vigo, Spain

Keywords: Correlated Tests, False Discovery Rate, Gene Expression Levels, Monte Carlo Simulations, Multitesting

Procedures.

Abstract: In a recent paper (de Uña-Álvarez, 2012, Statistical Applications in Genetics and Molecular Biology Vol.

11, Iss. 3, Article 14) a correction of SGoF multitesting method for possibly dependent tests was introduced.

This correction enhanced the field of applications of SGoF methodology, initially restricted to the

independent setting, to make decisions on which genes are differently expressed in group comparison when

the gene expression levels are correlated. In this work we investigate through an intensive Monte Carlo

simulation study the performance of that correction, called BB-SGoF (from Beta-Binomial), in practical

settings. In the simulations, gene expression levels are correlated inside a number of blocks, while the

blocks are independent. Different number of blocks, within-block correlation values, proportion of true

effects, and effect levels are considered. The allocation of the true effects is taken to be random. False

discovery rate, power, and conservativeness of the method with respect to the number of existing effects

with p-values below the given significance threshold are computed along the Monte Carlo trials.

Comparison to the classical Benjamini-Hochberg adjustment is provided. Conclusions from the simulation

study and practical recommendations are reported.

1 INTRODUCTION

Multiple-testing problems have received much

attention since the advent of the –omic technologies:

genomics, transcriptomics, proteomics, etc. They

often involve the simultaneous testing of hundreds

or thousands of hypotheses, or nulls, producing as a

result a number of significant p-values or effects

(that is, an increase in gene expression, or

RNA/protein levels). In this setup, the family-wise

error rate (FWER) and the false discovery rate

(FDR) have been proposed as suitable significance

criteria to perform the multiple testing. See

Benjamini and Hochberg (1995), Nichols and

Hayasaka (2003) or Dudoit and Laan (2008) for

basic definitions and reviews of existing literature.

As a drawback of FWER-based and FDR-based

methods, their power may be small when the number

of tests is large, or when the proportion of true nulls

is large and the effect in the non-true nulls is weak

relative to the sample size (Carvajal-Rodríguez et

al., 2009); (de Uña-Álvarez, 2011). Carvajal-

Rodríguez et al., (2009) introduced a new

multitesting strategy, SGoF (from Sequential

Goodness-of-Fit), which focuses on the difference

between the observed proportion of p-values below a

given significance threshold (the γ parameter) and

the expected one under the complete null of no

effects (γ); therefore, a binomial test for a proportion

is performed. SGoF approach provides a reasonable

compromise between false discoveries and power

(Carvajal-Rodríguez et al., 2009); the theoretical

statistical properties of SGoF were investigated in

detail in de Uña-Álvarez (2011). It was illustrated

that, with a large number of tests, the critical region

provided by SGoF is wider than that of FDR-based

methods in most practical scenarios. SGoF original

method provides reliable inference when the

multiple tests are independent.

However, in real world applications,

dependences among the tests will appear. This

dependence may be provoked by the existence of

several blocks of tests which share the same within-

Castro-Conde I. and de Uña-Álvarez J..

Performance of Beta-Binomial SGoF Multitesting Method for Dependent Gene Expression Levels - A Simulation Study.

DOI: 10.5220/0004191100930097

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 93-97

ISBN: 978-989-8565-35-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

block probability of reporting a significant p-value.

While FDR-based strategies are robust in

dependence scenarios, the same is not true for SGoF,

which crucially depends on the correct estimation of

the variance associated to the number of discoveries.

In most practical situations with dependent tests, the

final number of discoveries reported by SGoF will

be too liberal, because it will be based on an

underestimated variance (Owen, 2005). To solve this

issue, de Uña-Álvarez (2012) introduced a

correction of SGoF method to deal with dependent

tests. This correction is based on the beta-binomial

extension of the binomial model, which arises when

the number of successes S among the n trials is

conditionally distributed as a binomial given the

probability of success π, which is a random variate

following a beta distribution. The beta-binomial

model has three parameters: the number of trials n,

the mean probability of success p=E(π), and the

pairwise correlation between the outcomes

τ=Var(π)/p(1-p). The mean and the variance of the

beta-binomial model are given respectively by

E(S)=np and Var(S)=np(1-p)(1+(n-1)τ); this shows

that, by putting τ>0, the beta-binomial model allows

for a variance larger than binomial. See Johnson and

Kotz (1970) for further details and illustrations of

the model.

More specifically, given the set of n p-values

,…,u

coming from the n nulls being tested, BB-

SGoF (from beta-binomial SGoF) correction starts

by computing the binary sequence X

=I(u

≤γ),

i=1,…,n. Then, by assuming that there are k

independent blocks of p-values of sizes n

,…,n

(with n

+…+n

=n), the number of successes sj

within each block j is computed. Here, X

=1 is called

‘success’. Each s

is assumed to be a realization of a

beta-binomial variable with parameters (n

,p,τ). In

this setting, p represents the average proportion of p-

values falling below γ, which under the complete

null is just γ, and τ is the within-block correlation

between two outcomes X

and X

. Estimation of p

and τ is performed by maximum-likelihood, and the

lower bound of a 100(1-α)% interval for the excess

of significant cases n(p-γ) is reported; this bound is

the number of effects declared by BB-SGoF (which

weakly controls FWER at level α in this manner).

Therefore, BB-SGoF follows the same spirit of

SGoF method, but some preliminary estimation of

the p-values’ dependence structure is performed to

correct for it. This correction may have a big impact

in the researcher’s decision; for example, de Uña-

Álvarez (2012) illustrates for two real datasets that

ordinary SGoF rejects 10% (Hedenfalk data) or

about 4% (Diz data) nulls more than BB-SGoF, and

that BB-SGoF rather than SGoF should be applied

due to significant correlation.

Simulations in de Uña-Álvarez (2012) for n=500

and n=1000 tests reported the mean and standard

deviation of the number of rejections for SGoF-type

methods, as well as the family-wise rejection rate

(which reduces to the FWER and FDR under the

complete null of no effects); these simulation results

showed that BB-SGoF is able to control FWER at

level α even when the number of blocks k is

unknown (which is the usual situation in practice),

provided that some conservative criterion in the

estimation of k is used. Besides, this conservative

criterion did not result in a great loss of power

(compared to the ‘benchmark’ method based on the

true value of k). Ordinary SGoF performed badly

otherwise, being unable to control for dependences

(as expected). However, the simulation study

reported in the referred paper has some limitations.

First, no computation of the FDR in the presence of

effects was made, neither results on the methods’

power were reported. This was because of the

employed simulation procedure, which does not

allow for distinguishing between true and non-true

nulls. Also because of this, comparison to the

Benjamini-Hochberg (BH) FDR-controlling

procedure was not possible. Second, the simulated

model was a beta-binomial, and therefore the

simulations are useless to know how the beta-

binomial approach will work in other scenarios with

blocks of dependent tests. The simulation study in

the present work aims to overcome these limitations.

The rest of the paper is organized as follows. In

Section 2 we describe the simulated setting. In

Section 3 we report the results of our simulation

study, and we summarized them in a number of

relevant findings. A final discussion is reported in

Section 4.

2 SIMULATED SETTING

Having in mind the study of Hedenfalk data (see e.g.

de Uña-Álvarez, 2012), we simulated n=500 or

n=1000 2-sample t-tests for comparison of normally

distributed ‘gene expression levels’ in two groups A

and B with sizes 7 and 8 respectively. The

proportion of true nulls (i.e. genes equally

expressed) Π

was 1 (complete null), 0.9 (10% of

effects), or 0.67 (33% of effects). Mean was always

taken as zero in group A, while in group B it was μ

for 1/3 of the effects and –μ for the other 2/3 of

effects, with μ=1 (weak effects), μ=2 (intermediate

effects), or μ=4 (strong effects). Random allocation

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

of the effects among the n tests (genes) was

considered. Within-block correlation levels of ρ=0,

0.1, 0.2 and 0.8 were taken. With regard to the

number of blocks, we considered k=10 or k=20, so

we had 50 or 25 tests per block when n=500, and

100 or 50 tests per block when n=1000. For random

generation, the function rmvnorm of the R software

was used.

BB-SGoF method with γ=α=0.05 was applied

under perfect knowledge on the true value of k but

also when underestimating (k/2) or overestimating

(2k) the true number of blocks. The blocks were

always constructed homogeneous in size. We also

applied an automatic (data-driven) choice of k by

minimizing the number of effects declared by BB-

SGoF along the grid k=2,…,61. For γ=0.05, 5% of

the p-values are expected to fall below γ under the

complete null, while this amount rises to about

17.8%, 34.9% and 36.7% when e.g. there is a 33%

of weak, intermediate, or strong effects respectively.

The estimated values of the within-block correlation

τ between indicators X

=I(u

≤γ) and X

=I(u

≤γ) in the

simulations were much smaller than the within-

block correlation ρ between the ‘gene expression

levels’, ranging from about 0.002 to 0.232

depending on ρ.

1000 Monte Carlo simulations were performed.

For each situation, we computed the FDR, the power

(both averaged along the 1000 trials), and the

proportion of trials for which the number of declared

effects was not larger than the number of effects

with p-value below γ (this is just 1-FDR under the

complete null); as indicated in de Uña-Álvarez

(2012), BB-SGoF guarantees that this proportion

(labeled as Cov from ‘coverage’ in Tables below) is

asymptotically (i.e. n→∞) larger than or equal to 1-

α, a property which is not shared by other

multitesting methods. Computation of these

quantities for the original SGoF method for

independent tests and for the BH method (with a

nominal FDR of 5%) was also included to compare.

3 SIMULATION RESULTS

Tables 1 to 6 reported in this section are a sample of

the full set of results of our simulations. They are

restricted to case k=10, n=1000, no effects or 33%

of effects, weak or strong effects (μ=1 or μ=4), and

within-block correlation ρ=0 (independent setting),

ρ=0.2 (moderate correlation), and ρ=0.8 (strong

correlation). Other cases reported similar results (not

shown).

Starting with the case of no effects, we see from

Tables 1, 3 and 5 that all the methods respect the

nominal FWER (FDR) of 5% fairly well in the

independent setting. The automatic BB-SGoF

reports an FDR below nominal, something expected

due to its conservativeness. As correlation grows,

original SGoF for independent tests loses control of

FWER; when ρ=0.8, it is almost 7 times the

nominal. On the other hand, BB-SGoF methods

adapt well to the correlated settings (particularly true

for the benchmark method which uses the true k, and

for the automatic method), while BH method

respects the nominal FDR (expected, due to its

robustness for dependences) but it is very

conservative in the case ρ=0.8. The FWER of BB-

SGoF is above the nominal when the researcher

overestimates the number of blocks; this is because

BB-SGoF decision becomes more liberal as the

assumed dependence structure gets weaker.

Summarizing, the results for BB-SGoF are relevant

since they suggest FWER control even when the

simulated model is not beta-binomial.

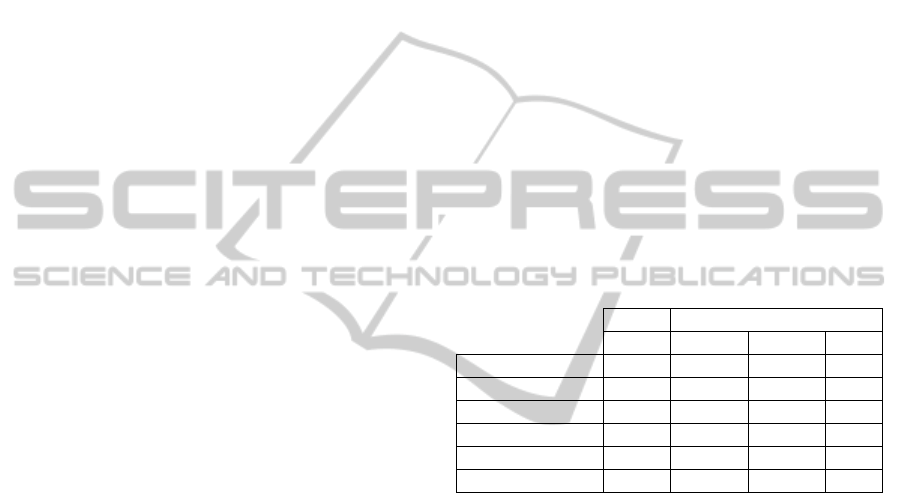
Table 1: n=1000, ρ=0, k=10, μ =1 (see text).

=1 Π

=0.67

FDR FDR Power Cov

SGoF

0.048 0.1260 0.2852 1

0.057 0.0353 0.0301 1

BB-SGoF (k)

0.047 0.1246 0.2808 1

BB-SGoF (k/2)

0.044 0.1239 0.2790 1

BB-SGoF (2k)

0.044 0.1250 0.2821 1

Auto BB-SGoF

0.019 0.1193 0.2679 1

The situation with 33% of weak effects (μ=1,

Tables 1, 3 and 5) reveals that SGoF-type strategies

are not controlling FDR at any given level. For

example, in the independent setting, original SGoF

and benchmark BB-SGoF report a FDR of 12.6%

and 12.5% respectively, two times and a half the

nominal FDR for BH procedure. Results for the

dependent setting are of the same order, although for

strong correlation (ρ=0.8) these FDRs go down to

10.9% and 8.5% respectively. However, the

proportion of true effects detected by SGoF-type

methods is between 5 and 9 times that of BH, the

relative performance of SGoF getting better as

correlation decreases. At the same time, one may say

that BB-SGoF is not detecting ‘too many effects’ in

the sense that, in at least 98.1% of the trials (worst

situation), the number of declared effects is below

the number of true effects with p-value below γ. It is

not strange that this proportion is just 100% for BH

since this method is rejecting only between 3% and

4% of the existing effects. Interestingly, automatic

BB-SGoF does not lose much power to respect to its

PerformanceofBeta-BinomialSGoFMultitestingMethodforDependentGeneExpressionLevels-ASimulationStudy

optimal version based on the true number of blocks:

its power is 6.4% smaller in the worse situation

(ρ=0.8).

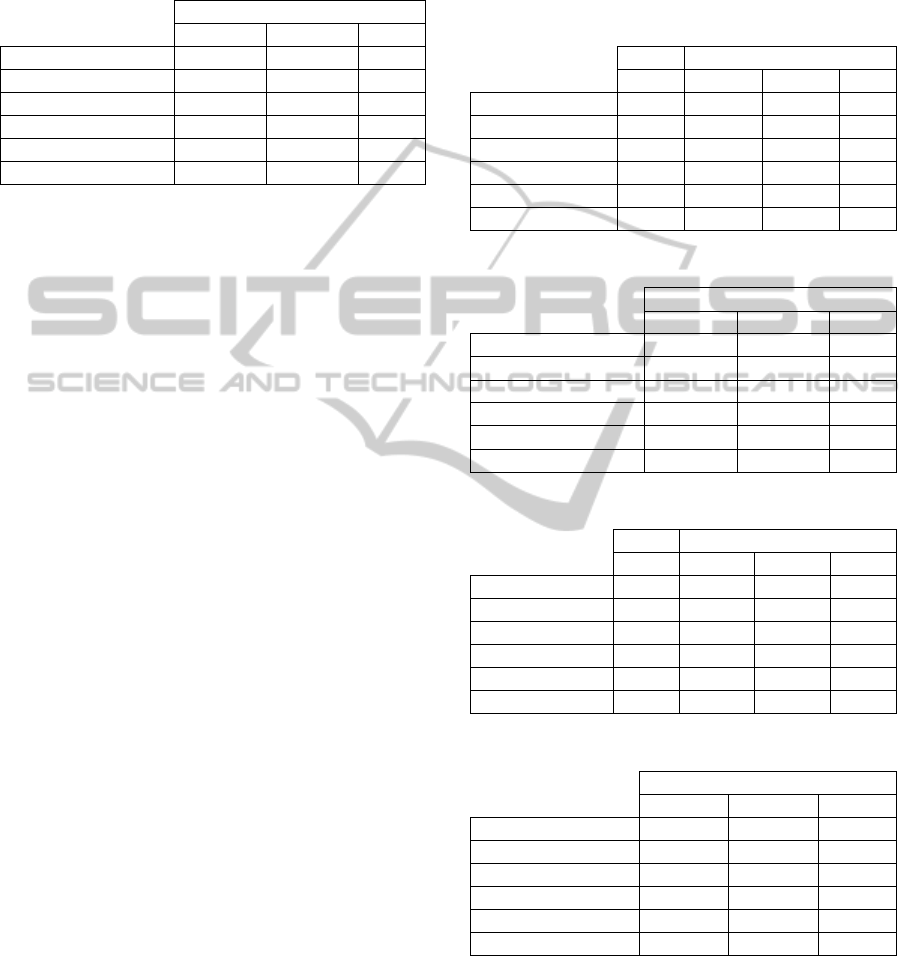
Table 2: n=1000, ρ=0, k=10, μ =4 (see text).

=0.67

FDR Power Cov

SGoF

0.0001 0.8779 1

0.0333 1.0000 0

BB-SGoF (k)

0.0001 0.8693 1

BB-SGoF (k/2)

0.0001 0.8662 1

BB-SGoF (2k)

0.0001 0.8717 1

Auto BB-SGoF

0.0001 0.8533 1

The case with 33% of strong effects (μ=4, Tables

2, 4 and 6) allows to see that, in some instances, the

FDR of SGoF-type methods may be very small

compared to γ (the p-value threshold) or α (the

FWER-controlling parameter under the complete

null). Tables indicate that, for the simulated settings,

the average proportion of false discoveries of

benchmark BB-SGoF lies between 0.07/1000 and

0.4/1000, being even smaller for its automatic

version. The reason for this is that, with such strong

effects, the non-true nulls report very small p-values,

which are clearly separated from those of the true

nulls. Still, automatic BB-SGoF is able to detect

more than 80% of the existing effects. The power of

BH procedure is larger than that, according to its

higher FDR; indeed, this power is almost 100%.

This situation may be regarded as non-optimal

however, in the sense of the coverage; for example,

in the case ρ=0.8 (Table 6), only for 17% of the

1000 Monte Carlo trials the number of effects

declared by BH was below the true number of

effects with p-value smaller than 0.05, showing an

anticonservative performance in this sense (this

percentage was even smaller for the other correlation

levels). Also importantly, as for the case with weak

effects, the automatic choice of the number of blocks

results in a small loss of power (smaller than 2.5% in

this case).

The number of blocks of dependent tests

detected by automatic BB-SGoF was not always

close to the true k (k=10). For example, under the

complete null it was 18.1 (independent setting), 10.4

(ρ=0.2), or 6.9 (ρ=0.8) on average, therefore being

decreasing with an increasing correlation.

Corresponding standard deviations were 16.7, 12.4,

and 10.5, showing a large variability of the selected

number of blocks along replicates. The average

number of blocks detected was decreasing for an

increasing proportion of effects and also for more

distant alternatives (stronger effects). Whatever the

case, one should keep in mind that the role of

automatic BB-SGoF is not to perfectly estimate the

number of existing blocks but rather to allow for

error control in the multitesting procedure when the

value of k is unknown.

Table 3: n=1000, ρ=0.2, k=10, μ =1 (see text).

=1 Π

=0.67

FDR FDR Power Cov

SGoF

0.145 0.1277 0.2849 1

0.05 0.0302 0.0305 1

BB-SGoF (k)

0.064 0.1238 0.2745 1

BB-SGoF (k/2)

0.077 0.1238 0.2745 1

BB-SGoF (2k)

0.092 0.1251 0.2785 1

Auto BB-SGoF

0.042 0.1202 0.2634 1

Table 4: n=1000, ρ=0.2, k=10, μ =4 (see text).

=0.67

FDR Power Cov

SGoF

0.0001 0.8783 1

0.0334 1 0

BB-SGoF (k)

0.0001 0.8674 1

BB-SGoF (k/2)

0.0001 0.8650 1

BB-SGoF (2k)

0.0001 0.8707 1

Auto BB-SGoF

0.0001 0.8503 1

Table 5: n=1000, ρ=0.8, k=10, μ =1 (see text).

=1 Π

=0.67

FDR FDR Power Cov

SGoF

0.341 0.1088 0.2813 0.886

0.028 0.0263 0.0409 1

BB-SGoF (k)

0.059 0.0847 0.2195 0.992

BB-SGoF (k/2)

0.049 0.0857 0.2257 0.995

BB-SGoF (2k)

0.118 0.0936 0.2434 0.981

Auto BB-SGoF

0.024 0.0778 0.2054 0.999

Table 6: n=1000, ρ=0.8, k=10, μ =4 (see text).

=0.67

FDR Power Cov

SGoF

0.0050 0.8708 0.91

0.0320 0.9999 0.17

BB-SGoF (k)

0.0004 0.8258 0.995

BB-SGoF (k/2)

0.0003 0.824 0.996

BB-SGoF (2k)

0.0012 0.8458 0.982

Auto BB-SGoF

0.0001 0.8053 1

We end this section by mentioning that the

simulations with n=500 tests or with k=20 blocks

reported basically the same results as those provided

in Tables 1 to 6. However, important differences

were seen when considering a smaller number of

effects (10% instead of 33%) or intermediate effects

(μ=2) rather than weak (μ=1) or strong (μ=4) effects.

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

For example, with 10% of weak effects, the power

of automatic BB-SGoF relative to BH was above 17

under independence and above 15 with ρ=0.2, being

also true that BB-SGoF showed a FDR more than

twice its value with 33% of weak effects. On the

other hand, with 33% of intermediate effects, BH

and BB-SGoF procedures performed similarly in

FDR and power.

4 DISCUSSION

In this work we have investigated through

simulations the performance of BB-SGoF method.

Rate of false discoveries (FDR), proportion of

detected effects (power), and conservativeness with

respect to the true number of effects with p-value

smaller than the given threshold have been

computed. One conclusion of our research is that

BB-SGoF method may control for FWER in the

weak sense even when the underlying model is not

beta-binomial. BB-SGoF method is also robust with

respect to miss-specification of the number of

existing blocks, although it becomes too liberal

when this parameter is overestimated. As a

compromise, the automatic BB-SGoF procedure

introduced in de Uña-Álvarez (2012) performs well,

with only a small loss of power with respect to the

benchmark version. Summaryzing, BB-SGoF is a

correction of SGoF method with a suitable error

control in the presence of dependent tests; its

advantages over classical FDR-controlling strategies

(e.g. the BH method) remain the same in the

dependence scenario as for SGoF in the independent

setting, these are: greater power in the case of large

number of tests and small to moderate number of

weak effects. In such cases application of BB-SGoF

is recommended due to its compromise between

FDR and power.

ACKNOWLEDGEMENTS

Work supported by the Grants MTM2008-03129

and MTM2011-23204 (FEDER support included) of

the Spanish Ministry of Science and Innovation.

Support from the Xunta de Galicia Grant

10PXIB300068PR is also acknowledged. This work

was also supported by Agrupamento INBIOMED,

2012/273, from DXPCTSUG-FEDER ‘Unha

maneira de facer Europa’.

REFERENCES

Benjamini Y., Hochberg Y., 1995. Controlling the False

Discovery Rate: A Practical and Powerful Approach to

Multiple Testing. Journal of the Royal Statistical

Society Series B (Methodological) 57, 289-300.

Carvajal-Rodríguez A., de Una-Álvarez J., Rolan-Alvarez

E., 2009. A new multitest correction (SGoF) that

increases its statistical power when increasing the

number of tests. BMC Bioinformatics 10:209.

de Uña-Álvarez J., 2011. On the statistical properties of

SGoF multitesting method. Statistical Applications in

Genetics and Molecular Biology Vol. 10, Issue 1,

Article 18.

de Uña-Álvarez J., 2012. The beta-binomial SGoF method

for multiple dependent tests. Statistical Applications in

Genetics and Molecular Biology Vol. 11, Issue 3,

Article 14.

Dudoit S., van der Laan M., 2008. Multiple Testing

Procedures with Applications to Genomics. New

York: Springer.

Johnson N. L., Kotz, 1970. Distributions in statistics,

continuous univariate distributions-2. Houghton

Mifflin, Boston.

Nichols T., Hayasaka S., 2003. Controlling the familywise

error rate in functional neuroimaging: a comparative

review. Statistical Methods in Medical Research 12,

419-446.

Owen A., 2005. Variance of the number of false

discoveries. Journal of the Royal Statistical Society

Series B-Statistical Methodology 67, 411-426.

PerformanceofBeta-BinomialSGoFMultitestingMethodforDependentGeneExpressionLevels-ASimulationStudy