
Influence of Pipette Geometry on the Displacement Profile of Isotropic
Materials used for Vocal Fold Modeling
Sandra Weiß
1
, Scott L. Thomson
2
, Alexander Sutor
1
, Stefan J. Rupitsch
1
and Reinhard Lerch
1
1
Chair of Sensor Technology, Friedrich-Alexander-University, Erlangen, Germany
2
Department of Mechanical Engineering, Brigham Young University, Provo, Utah, U.S.A.
Keywords:
Pipette Aspiration, Vocal Folds, Inverse Method, Rectangular Cross-sectional Pipette.
Abstract:
Due to limited access to human vocal folds, synthetic vocal folds are used to study periodic phonation. With
respect to a realistic replica, the properties of the synthetic material should be to those of as real tissue. Sil-
icone rubber is a commonly used material for vocal fold models. A suitable method to analyze the material
parameters of both artificial and real vocal folds is the pipette aspiration technique. In the present study, the
displacement profiles of an isotropic silicone specimen were measured with three different pipette geometries.
The experimental results were compared to finite element simulations of the setup based on frequency depen-
dent material parameters extracted from a previous study. The results demonstrate the potential of the pipette
aspiration technique for material characterization and validate the determination of material parameters by
means of an Inverse Method. Furthermore, a possible parameter for the classification of anisotropic materials
is proposed and the suitability of the different pipette geometries for material characterization is discussed.
1 INTRODUCTION
Flow-induced vibrations of the vocal folds (phona-
tion) initiate the sound for most human voicing. In
order to better understand the periodic parts of phona-
tion, the vibratory characteristics of the vocal folds
have to be analyzed. The vocal folds are comprised
of multiple layers of tissues with different properties.
Their morphology can be divided into three main re-
gions (Hirano, 1981): the body, the ligament, and the
cover. The cover is the most superficial layer and is
mainly composed of an extracellular matrix and loose
fibers (Gray, 2000). In contrast, the ligament (middle
layer) contains a high density of elastin and spiraling
collagen fiber bundles oriented in anterior-posterior
direction, leading to a transversely isotropic material
behavior (Hammond et al., 1997). The deepest and
thickest layer (body) consists of muscle fibers (Finck
and Dejeune, 2010).
Due to limited in vivo access to human vocal folds
and rapid degradation of excised larynges, artificial
vocal folds are being increasingly used to study the
mechanics of flow-induced vibration. It is important
that these replicas possess similar material properties
as real tissue. Because silicone rubber offers similar
stiffness characteristics, vocal fold models have been
fabricated using this material. Different approaches,
including single-layer models (Becker et al., 2009)
and multi-layer models with variations in stiffness be-
tween the layers (Pickup and Thomson, 2009) have
been presented.
In order to compare the properties of synthetic
model materials with those of real vocal fold tissue,
there is a need for measurement methods capable of
determining the mechanical material parameters of
these types of synthetic materials and tissues over a
range of physiologically-realistic frequencies. In the
following, some candidate techniques are briefly sum-
marized and assessed, noting the ultimate goal of im-
provement of the clinical care of the human voice.
The measurement of the static elasticity modu-
lus of synthetic and real vocal folds is performed
by tensile tests (Alipour-Haghighi and Titze, 1991).
However, the properties of real vocal fold tissue are
frequency-dependent (Chan and Titze, 1999). Conse-
quently, measurement techniques to analyze the dy-
namic behavior are needed.
The frequency-dependent material parameters of
single layer silicone samples can be measured with
a so-called vibration transmission analyzer (Rupitsch
et al., 2011). In this approach, an isotropic silicone
specimen with known geometry is mounted on an
electromechanical shaker. A harmonic oscillation is
induced at the bottom surface, the velocity of which
108
Weiß S., L. Thomson S., Sutor A., J. Rupitsch S. and Lerch R..
Influence of Pipette Geometry on the Displacement Profile of Isotropic Materials used for Vocal Fold Modeling.
DOI: 10.5220/0004191801080113
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2013), pages 108-113
ISBN: 978-989-8565-34-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
is measured with an acceleration sensor. The velo-
city at the centerpoint of the specimen’s top surface is
measured with a laser vibrometer. The magnitude of
the transfer function between the two velocities is cal-
culated over a frequency range of 10 -400 Hz. The ex-
perimental results are compared to corresponding fi-
nite element simulation results and the dynamic mate-
rial parameters are estimated using an Inverse Method
(Rupitsch and Lerch, 2009). Although, this method
provides dynamic information, only specimens with
known geometry can be investigated, which typically
precludes investigations of real tissue.
One possible method for the material character-
ization of real and artificial vocal fold materials is
the pipette aspiration technique. A first approach
to estimate the static elasticity modulus of homo-
geneous, isotropic materials was published in (Aoki
et al., 1997). It was shown that by placing a pipette
on a soft material and applying static suction, the
Young’s modulus of that region can be calculated
by measuring the maximum aspiration displacement
as a function of aspiration pressure. Further studies
have applied this technique to real tissue, e.g., (Mat-
sumoto et al., 2002; Henriksen and Ipsen, 2004). By
replacing the static pressure with a fluctuating pres-
sure, frequency-dependent analysis has been enabled
(Z
¨
orner et al., 2010). Moreover, in (Ohashi et al.,
2005) the technique was applied to the measurement
of anisotropic properties of blood vessels under biax-
ial stretch. It was shown that by using a rectangular
cross-sectioned pipette, the static elasticity modulus
along the length could be neglected. As a result, by
choosing an appropriate pipette geometry, anisotropic
regions can be characterized. Moreover, the suit-
ability of the pipette aspiration technique for the char-
acterization of inhomogeneous transversely isotropic
silicone samples was recently demonstrated by (Weiss
et al., 2013). All these studies show the potential of
the pipette aspiration technique for determining the
material properties of synthetic materials and real tis-
sue. The technique is spatially-resolved and it could
potentially be used in in vivo investigations. There-
fore, this method could help in the development of a
more realistic vocal fold model by comparing mea-
surements of synthetic materials to those of real tis-
sue.
In this paper, we focus on the feasibility of the
proposed measurement method by measuring the dis-
placement profiles of isotropic silicone samples with
three different pipette geometries at a frequency of
120 Hz. The experimental results are compared with
finite element predictions using a model with material
properties taken from (Rupitsch et al., 2011), validat-
ing the experimental procedure as well as the deter-
mination of the material parameters.
2 MATERIALS AND METHODS
2.1 Silicone Specimens
The two-part addition-cure silicone rubber
Ecoflex 0030 (Smooth-On, Inc.) was used to
fabricate cuboid silicone specimens measuring
50 mm × 50 mm × 10 mm. This material consists
of equal parts of the two subcomponents. By adding
a variable amount of silicone thinner, the specimen’s
stiffness is reduced. In this study, mixtures with three
parts of thinner (namely 1:1:3) were used. The static
elasticity modulus of samples made using this mixing
ratio has been previously measured using tensile tests
to 7.02 kPa ± 0.29 kPa (Ilg et al., 2012).
2.2 Pipette Aspiration Setup
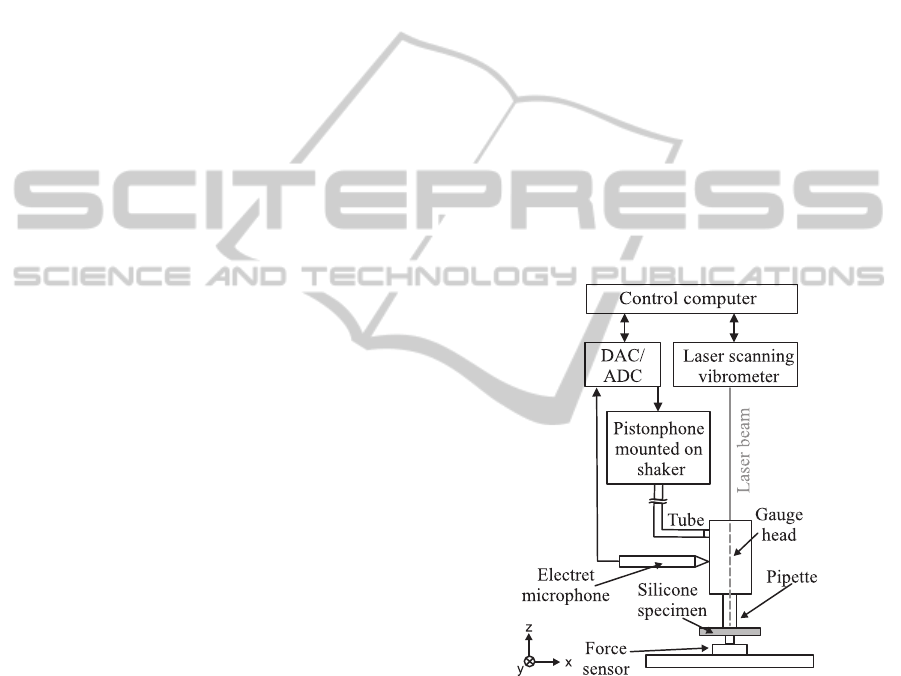
Figure 1: Pipette aspiration setup.
The measurement setup is shown in Figure 1. The
specimen was positioned on a plate. The pipette
was pressed against the surface of the specimen and
the contact force, measured by the force sensor, was
maintained at 0.2 N. The gauge head was connected
to a pistonphone that was mounted on a shaker to
generate a fluctuating pressure within the gauge head.
The excitation frequency (here 120 Hz) and ampli-
tude of the mechanical oscillation were controlled via
LabVIEW
c
⃝
. The actual pressure amplitude was ac-
quired by the microphone and kept constant at 20 Pa.
Using a laser scanning vibrometer (PSV 300, Poly-
tec), the out-of-plane velocity at several points on a
InfluenceofPipetteGeometryontheDisplacementProfileofIsotropicMaterialsusedforVocalFoldModeling
109

measurement grid coinciding with the aspiration area
of the pipette was measured.
2.3 Pipette Configurations
For the experiments, three pipettes of different end
geometries were applied, and the resulting displace-
ment profiles were analyzed. The top views of the
pipette cross sections are schematically shown in Fig-
ure 2. One pipette was circular with an inner dia-
meter of 3 mm and an outer diameter of 12 mm (Fig-
ure 2a)). Another pipette had a rectangular cross sec-
tion (Figure 2b)) with outer dimensions of the pipette
area of 12 mm × 12 mm. The aspiration area mea-
sured 4 mm × 1 mm. Finally, a cross-shaped pipette
(Figure 2c)) with similar pipette size was used. The
long axis measured 4 mm and the short axis measured
1.5 mm.
Figure 2: Pipette configurations investigated in this study:
a) circular, b) rectangular and c) cross-shaped measurement
areas.
2.4 Finite Element Simulations
Finite element simulations were performed to (i) ex-
plore the dynamic material properties proposed in
(Rupitsch et al., 2011), (ii) to validate the simulations
by comparison with experiments, and (iii) investigate
the influence of different pipette configurations on the
measured displacement profiles.
2.4.1 Simulation Model
Figure 3 shows the three-dimensional finite element
model geometry of the measurement system with a
cross-shaped pipette. The cuboid specimen with an
edge length of 50 mm and a height of 10 mm was
modeled using the ANSYS
c
⃝
preprocessor and solved
using the finite element software CFS++ (Coupled
Field Simulation) (Kaltenbacher, 2007). The pipettes
were modeled as the ends of either an annulus or a
hollow block. The total number of nodes and ele-
ments for the different models are summarized in Ta-
ble 1.
50 mm
50 mm
10 mm
Silicone
rubber
Pipette wall
Aspiration area
Figure 3: Finite element model geometry with a cross-
shaped pipette.
Regarding boundary conditions, the bottom nodes
of the cuboid were fixed to simulate the silicone speci-
men placement on a plate in the experiment. Since
the experiments were performed with a contact force
of 0.2 N, a static analysis was executed in the first
step of the simulations, applying an appropriate pres-
sure on the pipette wall. Harmonic analysis with fixed
boundary conditions at the pipette wall was then per-
formed. The specimen surface displacement within
the aspiration area was calculated for a 120 Hz fluctu-
ating pressure with an amplitude of 20 Pa.
2.4.2 Input Material Parameters
The dynamic material parameters were extracted from
(Rupitsch et al., 2011). In that study, the frequency-
dependent Young’s modulus, damping factor, and
Poisson’s ratio values of a cylindrically-shaped sili-
cone sample with the same mixing ratio were deter-
mined using an inverse scheme (Rupitsch and Lerch,
2009) based on a Gauss-Newton algorithm. The re-
sults served as input parameters for the performed
simulations and are therefore briefly summarized.
The Poisson’s ratio was calculated to remain constant
over frequency with a value of 0.499. The damp-
ing factor was estimated to be 0.13. The following
frequency-dependent real and imaginary parts of the
Young’s modulus of the 1:1:3 silicone mixture were
obtained
E
R
( f )
Pa
= 7.02 · 10
3
+9.82 ·
f
Hz
+ ...
··· + 8.59 · 10
2
· log
10
(
f
Hz
+ 1
)
E
I
( f )
Pa
= 3.85 · 10
3
+11.5 ·
f
Hz
+ ...
··· − 1.13 · 10
3
· log
10
(
f
Hz
+ 1
)
.
BIODEVICES2013-InternationalConferenceonBiomedicalElectronicsandDevices
110

3 RESULTS
The displacement profiles of an isotropic 1:1:3 sil-
icone specimen were measured using the pipettes
shown in Figure 2. A circular measurement grid was
used for the circular pipette and a quadratic grid was
used for the rectangular and cross-shaped pipettes, re-
spectively. To ensure acquisition throughout the aspi-
ration area, the measurement grid extended beyond
the aspiration area by about 0.5 mm along each edge.
The top view and the profile cross sections in or-
thogonal x- and y-directions are shown in the sec-
ond and third columns of Figure 4, respectively. The
dashed lines show the profiles in the y-direction, the
solid lines in the x-direction. Due to reflections at
the pipette wall, the edges of the area enclosed by the
pipette are diffuse and the displacements at the grid
edges are overestimated and therefore not zero.
Table 1: Numbers of nodes and elements for the different
finite element models. The numbers in parentheses list the
nodes and elements within the aspiration area.
Pipette Nodes Elements
circular 68605 (3364) 46583 (1200)
rectangular 73794 (2185) 54149 (1152)
cross-shaped 66500 (1617) 50132 (858)
The measurement results are compared to those
of the finite element simulations, described in Sec-
tion 2.4. The fourth and fifth columns of Figure 4
show the computational results. The comparison of
the profile cross sections shows very good quanti-
tative agreement between the experimental and the
computational displacements. Moreover, the profile
shapes of both simulations and experiments are simi-
lar.
The computational results also demonstrate that
the determination of the dynamic material parameters
with the vibration transmission analyzer (Rupitsch
et al., 2011) by means of an inverse scheme is suitable
for synthetic materials used for vocal fold modeling.
This is evidenced by the calculated material parame-
ters serving as input for the finite element simulations
in this study. The presented results provide evidence
that both platforms (numerical and experimental ap-
proaches) are valid tools for exploring various exten-
sions and applications of the pipette aspiration tech-
nique pertaining to material property characterization.
With respect to the profile cross sections, the cir-
cular pipette showed a parabolic form and axisym-
metric profiles. The profiles of the cross-shaped
pipette matched as well. Both measurements with
the rectangular pipette (see Figure 2b)) yielded sim-
ilar cross sections along long and short axes. As we
investigated an isotropic specimen, this was expected.
However, parts of the human vocal folds exhibit a
transversely isotropic behavior. In a previous study
(Ohashi et al., 2005), a rectangular pipette was used
for the measurement of anisotropic material proper-
ties. It was found that the elasticity along the length
can be neglected. Consequently, the displacement
profiles of the circular and cross-shaped pipette were
supposed to deviate from axisymmetry in case of a
transversely isotropic specimen. For the rectangular
pipette, the displacements for the two configurations
in Figure 2b) would be different. For that reason, we
propose a new measure, the numerical parameter A
∗
,
to quantify the degree to which the investigated ma-
terial exhibits anisotropic behavior. The area of the
x-profile, A
x
, can be calculated by integrating the dis-
placements, d(x,0) in the x -z-plane for y = 0 over the
x-direction span, l:
A
x
=
+
l
2
∫
−
l
2
d(x,0)dx. (1)
For the orthogonal y-direction, the corresponding
area is calculated by
A
y
=
+
l
2
∫
−
l
2
d(0,y)dy. (2)
The ratio of these two areas, A
∗
= A
y
/A
x
, quanti-
fies the deviation of the profile from axisymmetry.
Table 2: A
∗
-values for the measured and simulated profiles
shown in Figure 4.
Pipette
A
∗
Experiment Simulation
circular 1.01 1.00
rectangular (length l) 0.99 1.00
rectangular (width w) 0.99 1.00
cross-shaped 0.99 1.00
The displacement profiles were analyzed with re-
spect to A
∗
. Since the profile of the rectangular pipette
was not axisymmetric, the two configurations shown
in Figure 2b) were compared. The displacements over
the length l of both configurations were integrated and
divided by each other to calculate the A
∗
-value for
the profiles parallel to the long axis of the rectangu-
lar area. The A
∗
-value for the profiles parallel to the
width w were similarily obtained. The A
∗
-results are
summarized in Table 2. For all specifications, the A
∗
-
value is equal or nearly equal to 1, which is consistent
with expectations of an isotropic material. According
InfluenceofPipetteGeometryontheDisplacementProfileofIsotropicMaterialsusedforVocalFoldModeling
111

0
1
2
3
Displacement (µm)
−1.5 x, y (mm) 1.5
x
y
0
1
2
3
Displacement (µm)
−1.5 x, y (mm) 1.5
x
y
0
0.5
1
Displacement (µm)
−2 x, y (mm) 2
x
y
0
0.5
1
Displacement (µm)
−2 x, y (mm) 2
x
y
0
0.5
1
Displacement (µm)
−2 x, y (mm) 2
x
y
0
0.5
1
Displacement (µm)
−2 x, y (mm) 2
x
y
0
1
2
3
Displacement (µm)
−2 x, y (mm) 2
x
y
0
1
2
3
Displacement (µm)
−2 x, y (mm) 2
x
y
Figure 4: Experimental and computational results for isotropic materials: The pipette geometry is schematically shown in the
left column, the top view and profile cross sections of the measured displacement profiles are plotted in the second and third
column, whereas the corresponding simulations are plotted in the last two columns.
to (Ohashi et al., 2005), anisotropic materials were
sensitive to the stiffness parallel to the width of the
rectangular pipette. As a result, for anisotropic mate-
rials, we expect that the A
∗
-value should differ from 1
and could therefore serve as a quantitative measure of
the degree of anisotropy.
4 DISCUSSION
Three different pipette geometries were utilized and
the displacement profiles of an isotropic silicone sam-
ple with properties similar to real vocal fold tissue
were measured. Moreover, the profile cross sec-
tions in orthogonal directions were analyzed and the
experimental results were compared to finite element
simulations of the setup. The results demonstrate that
the pipette aspiration technique is suitable for inves-
tigating soft materials used for vocal fold modeling.
Furthermore, the material parameter determination by
means of an Inverse Method (Rupitsch and Lerch,
2009) was validated as results from a previous study
(Rupitsch et al., 2011) served as input parameters for
the simulation.
To characterize whether the investigated material
is isotropic or exhibits anisotropic properties, the nu-
merical parameter A
∗
describing the deviation from
profile axisymmetry was introduced. The value tends
to 1 for isotropic materials whereas anisotropic mate-
rials lead to a value smaller or greater than 1, as has
been previously demonstrated (Weiss et al., 2013).
Because the applied pipette configurations
showed different profile cross sections, the present
pipette aspiration setup could be an appropriate
way to acquire information about inhomogeneous
and anisotropic regions of a specimen. The setup
can also be applied to measurements of real tissue.
Importantly, comparing such data from both synthetic
materials and real tissue will likely yield improve-
ments in synthetic material development, leading to
improved vocal fold models.
Two challenges are noted. First, aspiration areas
with a diameter smaller than 1 mm in the current setup
are not possible due to insufficient focusing of the
laser beam. A second issue is the sensitivity of the
results to the specimen’s roughness, which is yet to
be explored.
Future studies will deal with a computational
study on the displacement profiles of transversely
isotropic materials to determine an optimal pipette
configuration for investigations on such materials.
BIODEVICES2013-InternationalConferenceonBiomedicalElectronicsandDevices
112

5 CONCLUSIONS
The material characterization of silicone rubber used
for vocal fold modeling by means of pipette aspiration
was proposed. Different aspiration areas were com-
pared with respect to the resulting displacement pro-
files. Finite element simulations based on frequency-
dependent material parameters were performed which
showed similar results revealing the potential of both,
the pipette aspiration technique for the characteriza-
tion of soft materials and the determination of dy-
namic material parameters using an Inverse Method
(Rupitsch and Lerch, 2009). By calculating the ra-
tio of the areas of the displacement profiles in or-
thogonal directions, a quantitative parameter for an
isotropic material behavior was presented. Because
this study validates both, the measurement procedure
and the numerical model, it provides a basis for fu-
ture studies dealing with similar characterizations of
synthetic materials used for vocal fold modeling.
ACKNOWLEDGEMENTS
The presented work was supported by Deutsche
Forschungsgemeinschaft (DFG, German Research
Foundation), Grant No. FOR 894/2, and by Grant
Number R01DC009616 from the U.S. National In-
stitute on Deafness and Other Communication Disor-
ders (NIDCD). Dr. Thomson gratefully acknowledges
support as a visiting professor from the University of
Erlangen Graduate School in Advanced Optical Tech-
nologies (SAOT).
REFERENCES
Alipour-Haghighi, F. and Titze, I. R. (1991). Elastic models
of vocal fold tissues. Journal of the Acoustical Society
of America, 90:1326–1331.
Aoki, T., Ohashi, T., Matsumoto, T., and Sato, M. (1997).
The pipette aspiration applied to the local stiffness
measurement of soft tissues. Annals of Biomedical
Engineering, 25:581–587.
Becker, S., Kniesburges, S., and M
¨
uller, S. (2009).
Flow-structure-acoustic interaction in a human voice
model. Journal of the Acoustical Society of America,
125:1351–1361.
Chan, R. W. and Titze, I. R. (1999). Viscoelastic shear
properties of human vocal fold mucosa: measurement
methodology and empirical results. Journal of the
Acoustical Society of America, 106:2008–2021.
Finck, C. and Dejeune, L. (2010). Handbook of Mammalian
Vocalization, chapter Structure and oscillatory func-
tion of the vocal folds, pages 427–438. Elsevier.
Gray, S. D. (2000). Cellular physiology of the vocal folds.
Voice disorders and Phonosurgery I, 33:679–697.
Hammond, T. H., Zhou, R., Hammond, E. H., Pawlak, A.,
and Gray, S. D. (1997). The intermediate layer: A
morphologic study of the elastin and hyaluronic acid
constituents of normal human vocal folds. Journal of
Voice, 11(1):59–66.
Henriksen, J. R. and Ipsen, J. H. (2004). Measurement of
membrane elasticity by micro-pipette aspiration. The
European Physical Journal E, 14:149–167.
Hirano, M. (1981). Clinical examination of Voice. Springer.
Ilg, J., Rupitsch, S. J., Sutor, A., and Lerch, R. (2012). De-
termination of dynamic material properties of silicone
rubber using one-point measurements and finite ele-
ment simulations. IEEE Transactions on Instrumen-
tation and Measurement, 61:3031–3038.
Kaltenbacher, M. (2007). Numerical Simulations of Mecha-
tronic Sensors and Actuators. Springer.
Matsumoto, T., Abe, H., Ohashi, T., Kato, Y., and Sato,
M. (2002). Local elastic modulus of atheroscle-
rotic lesions of rabbit thoracic aortas measured by
pipette aspiration method. Physiological Measure-
ment, 23:635–648.
Ohashi, T., Abe, H., Matsumoto, T., and Sato, M. (2005).
Pipette aspiration technique for the measurement of
nonlinear and anisotropic mechanical properties of
blood vessels under biaxial stretch. Journal of Biome-
chanics, 38:2248–2256.
Pickup, B. A. and Thomson, S. L. (2009). Influence of
asymmetric stiffness on the structural and aerody-
namic response of synthetic vocal fold models. Jour-
nal of Biomechanics, 42:2219–2225.
Rupitsch, S. J., Ilg, J., Sutor, A., Lerch, R., and D
¨
ollinger,
M. (2011). Simulation based estimation of dynamic
mechanical properties for viscoelastic materials used
for vocal fold models. Journal of Sound and Vibration,
330:4447–4459.
Rupitsch, S. J. and Lerch, R. (2009). Inverse method to es-
timate material parameters for piezoceramic disc ac-
tuators. Applied Physics A: Material Science & Pro-
ceedings, 97:735–740.
Weiss, S., Thomson, S. L., Lerch, R., D
¨
ollinger, M., and Su-
tor, A. (2013). Pipette aspiration applied to the charac-
terization of nonhomogeneous, transversely isotropic
materials used for vocal fold modeling. Journal of the
Mechanical Behavior of Biomedical Materials, doi:
10.1016/j.jmbbm.2012.08.005.
Z
¨
orner, S., Kaltenbacher, M., Lerch, R., Sutor, A., and
D
¨
ollinger, M. (2010). Measurement of the elastic-
ity modulus of soft tissues. Journal of Biomechanics,
43:1540–1545.
InfluenceofPipetteGeometryontheDisplacementProfileofIsotropicMaterialsusedforVocalFoldModeling
113
