Algorithms for Acceptance in Argument Systems
Samer Nofal, Paul Dunne and Katie Atkinson
Computer Science Department, University of Liverpool, Liverpool, U.K.
Keywords:
Argumentation Frameworks, Preferred Extensions, Credulous Acceptance, Skeptical Acceptance.
Abstract:
We introduce algorithms that decide arguments’ acceptance in Dung’s system of argumentation. Under pre-
ferred semantics, there might be various extensions of acceptable arguments, and hence, the acceptance prob-
lem is concerned with deciding whether a given argument is in an extension or in all extensions. The new al-
gorithms decide the acceptance without truly enumerating all extensions. This is of interest in situations where
the acceptance problem is confined to a specific argument while the underlying argument system changes fre-
quently such as in a dialog setting. We analyze our algorithms in contrast to existing algorithms. Consistent
with experimental results, we argue that the new algorithms are more efficient with respect to running time.
1 INTRODUCTION
An argument system is a reasoning model that is
likely to be a mainstay for the study of diverse areas
such as decision support systems (see e.g. (Amgoud
and Prade, 2009)), machine learning (see e.g. (Moz-
ina et al., 2007)), and agents interaction in multi agent
systems (see e.g. (McBurney and Parsons, 2009)).
Following (Dung, 1995), an argument system con-
sists of a set of arguments and a binary relation that
represents the conflicting arguments. Then, a resolu-
tion to an argument system is captured by deciding the
acceptable arguments. Several argumentation seman-
tics have been proposed to characterize the acceptable
arguments (Baroni et al., 2011). Under preferred se-
mantics (defined in section 2), there might be multiple
extensions of acceptable arguments. Accordingly, if
an argument is in all preferred extensions then the ar-
gument is skeptically accepted. On the other hand, if
an argument is in a preferred extension then the argu-
ment is credulously accepted. The acceptance prob-
lem might be simply decided by enumerating all pre-
ferred extensions. However, in situations where the
problem is around deciding the acceptance of a spe-
cific argument then it is more efficient to not faithfully
compute the preferred extensions especially when the
underlying argument system is dynamic (i.e. changes
frequently such as in a dialog setting).
In this paper we aim at engineering algorithms for
the acceptance decision problem under preferred se-
mantics. After recalling the definition of argument
systems in section 2, we present in section 3 the new
algorithms that outperform, with respect to running
time, the algorithms of (Cayrol et al., 2003; Thang
et al., 2009; Verheij, 2007). To show the efficiency
gain we compare our algorithms with existing algo-
rithms analytically in section 4 while further experi-
mental evaluation is described in section 5. Lastly, we
discuss further related works and conclude the paper
in section 6.
2 PRELIMINARIES
We recall the definition of argument systems (Dung,
1995). An argument system is a pair (A, R) where A
is a set of arguments and R ⊆ A × A is a binary re-
lation. We refer to (x,y) ∈ R as x attacks y (or y is
attacked by x). An argument x is acceptable w.r.t.
S ⊆ A iff ∀(y,x) ∈ R, ∃z ∈ S : (z,y) ∈ R. S ⊆ A is
conflict free iff ∀x,y ∈ S : (x,y) /∈ R. S ⊆ A is an
admissible set iff it is conflict free and ∀x ∈ S : x is
acceptable w.r.t. S. A preferred extension is a max-
imal (w.r.t. ⊆ ) admissible set. An argument x is
skeptically accepted iff x is in every preferred ex-
tension, while x is credulously accepted iff x is in a
preferred extension. For example, consider the argu-
ment system depicted by the directed graph in figure 1
where the nodes are the arguments A = {u, v,w,x,y, z}
while the arcs are the attacks between arguments R =
{(u,w),(v,u), (w,z),(v,z),(z,x),(x,y),(y,x)}. Thus,
the preferred extensions are {v,w,x} and {v, w,y} and
therefore v and w are skeptically accepted while x and
y are credulously accepted.
34
Nofal S., Dunne P. and Atkinson K..
Algorithms for Acceptance in Argument Systems.
DOI: 10.5220/0004192400340043
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 34-43
ISBN: 978-989-8565-39-6
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

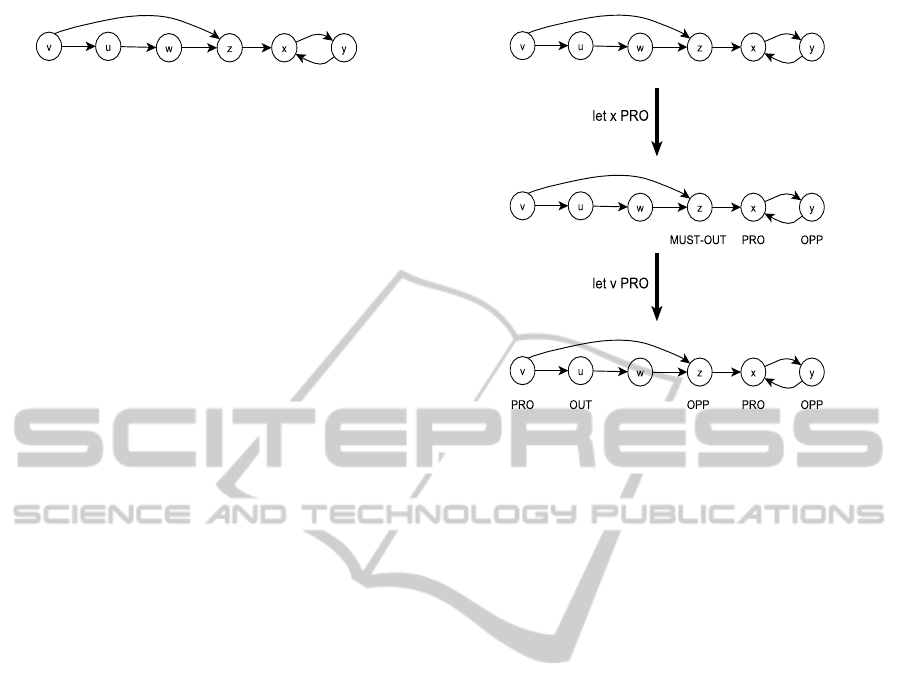
Figure 1: An argument system.
3 THE NEW ALGORITHMS
In deciding the acceptance, it might be desirable
to produce some kind of proof (i.e. explanation) as
to why an argument is credulously accepted. In order
to define what makes up a proof for the credulous ac-
ceptance let us recall a helpful term. We say that an
argument x is reachable from an argument y iff there
is a directed path from y to x. For example, in fig-
ure 1 x is reachable from u through the directed path
h(u,w),(w,z),(z,x)i while u is not reachable from x.
Thus, a credulous proof of a given argument is made
up of two sets; an admissible set containing the argu-
ment and the set of all counter arguments as formal-
ized in the following.
Definition 1. Let (A,R) be an argument system, S ⊆ A
be an admissible set containing x s.t. ∀z ∈ S : x is
reachable from z and let Q = {y ∈ A | ∃z ∈ S : (y,z) ∈
R}. Then, S∪ Q is a credulous proof for x.
It follows directly that our definition of credulous
proof is compatible with the definition of credulous
acceptance. Note that a given argument is credu-
lously accepted iff the argument is in an admissible
set, which is explicitly expressed in definition 1. Al-
gorithm 1 decides a credulous proof of an argument
by basically making use of five labels: PRO (short for
proponent), OPP (short for opponent), IGNO (short
for ignored), OUT and MUST-OUT. An argument x
is labeled PRO to indicate that x might be in an ad-
missible set and the argument in question is reach-
able from x. An argument y is labeled OUT iff y is
attacked by a PRO argument. The MUST-OUT la-
bel identifies arguments that attack PRO arguments.
An argument y is labeled OPP iff y is attacked by a
PRO argument and y attacks a PRO argument. An ar-
gument y is labeled IGNO to signal that y cannot be
in an admissible set with the current PRO arguments.
The formal usage of these labels is defined in algo-
rithm 1. The basic notion of algorithm 1 is to change
arguments’ labels iteratively according to the labels’
usage outlined earlier until there does not exist an ar-
gument that is MUST-OUT. At this point, PRO/OPP
arguments make up a credulous proof for the argu-
ment in question such that PRO arguments represent
the admissible part of the proof. Referring to the ar-
gument system in figure 1, {v,x, y,z} is a credulous
proof for x where {v,x} is admissible, see figure 2
that demonstrates how algorithm 1 works. Although
Figure 2: Deciding a credulous proof for x by algorithm 1.
figure 2 does not reflect every aspect of algorithm 1,
the figure might help the reader to capture the general
idea. To prove algorithm 1, it is essential to show that
PRO arguments make up an admissible set.
Proposition 1. Let (A,R) be an argument system and
x ∈ A. Then:
1. If algorithm 1 decides that x is credulously proved
by {y ∈ A | y is PRO or OPP } then ∃S ⊆ A : S is
admissible ∧ S = {y ∈ A | y is PRO}.
2. If x is credulously accepted then algorithm 1 de-
cides that x is credulously proved by {y ∈ A | y is
PRO or OPP }.
Proof: To prove both parts, we need to show that
{y ∈ A | y is PRO}, denoted by SS, is admissible. To
establish that SS is conflict free, assume that ∃z,y ∈
SS : (z,y) ∈ R, and so, y is OUT or OPP according
to algorithm 1, see lines 3-9 and 28-34. This con-
tradicts with the fact that y ∈ SS is PRO. To show
that ∀y ∈ SS : y is acceptable to SS, suppose that
∃y ∈ SS : ∃(z,y) ∈ R∧ 6 ∃w ∈ SS : (w, z) ∈ R, and sub-
sequently, z is MUST-OUT according to lines 12 and
37. This contradicts with the fact that SS is reported
as a credulous proof iff 6 ∃w ∈ A : w is MUST-OUT,
see line 25 and 47. ■
Referring to figure 1, x can be credulously proved
by either {v,x,z, y} or {u,v,w,x,y, z}. To decide more
credulous proofs for a given argument we define algo-
rithm 2 which is a slightly modified version of algo-
rithm 1 such that algorithm 2 continues searching for
further credulous proofs while algorithm 1 stops as
soon as a credulous proof is found. See figure 3 that
demonstrates how algorithm 2 finds the two credulous
proofs of the argument x in the argument system
AlgorithmsforAcceptanceinArgumentSystems
35

Algorithm 1: Deciding a credulous proof of an ar-
gument x in an argument system (A,R).
1 let C ∈ {true, f alse};
2 C ← true;
3 label x ∈ A PRO;
4 foreach (x,y) ∈ R do
5 if y ∈ A is MUST-OUT then
6 label y ∈ A OPP;
7 else
8 if y ∈ A is not OPP then
9 label y ∈ A OUT;
10 foreach (z,x) ∈ R do
11 if z ∈ A is IGNO or unlabeled then
12 label z ∈ A MUST-OUT;
13 C ← false;
14 else
15 if z ∈ A is OUT then
16 label z ∈ A OPP;
17 if C = true then
18 x is proved by {y ∈ A | y is PRO or OPP};
19 else
20 if is-accepted(A) = true then
21 x is proved by {y ∈ A | y is PRO or OPP};
22 else
23 x is not credulously acceptable;
24 procedure is-accepted(A)
25 foreach y ∈ A : y is MUST-OUT do
26 foreach (z, y) ∈ R : z ∈ A is unlabeled do
27 A
′
← A;
28 label z ∈ A
′
PRO;
29 foreach (z, u) ∈ R do
30 if u ∈ A
′
is MUST-OUT then
31 label u ∈ A
′
OPP;
32 else
33 if u ∈ A
′
is not OPP then
34 label u ∈ A
′
OUT;
35 foreach (v, z) ∈ R do
36 if v ∈ A
′
is IGNO or unlabeled then
37 label v ∈ A
′
MUST-OUT;
38 else
39 if v ∈ A
′
is OUT then
40 label v ∈ A
′
OPP;
41 if is-accepted(A
′
) = true then
42 A ← A
′
;
43 return true;
44 else
45 label z ∈ A IGNO;
46 return false;
47 return true;
48 end procedure
of figure 1. Since it would be similar to the proofof al-
gorithm 1, we omit the soundness proof of algorithm
2 to avoid redundancy. However, there is no guaran-
tee that algorithm 2 will return all credulous proofs.
Regarding the decision problem of skeptical ac-
ceptance, the proof for a skeptically accepted argu-
Algorithm 2: Deciding a set of credulous proofs of
an argument x in an argument system (A,R).
1 let pr f s denote a set of credulous proofs for x;
2 pr fs ← φ;
3 let C
1
∈ {true, false};
4 C
1
← true;
5 label x ∈ A PRO;
6 foreach (x,y) ∈ R do
7 if y ∈ A is MUST-OUT then
8 label y ∈ A OPP;
9 else
10 if y ∈ A is not OPP then
11 label y ∈ A OUT;
12 foreach (z,x) ∈ R do
13 if z ∈ A is IGNO or not labeled then
14 label z ∈ A MUST-OUT;
15 C
1
← false;
16 else
17 if z ∈ A is OUT then
18 label z ∈ A OPP;
19 if C
1
= true then
20 pr fs ← pr fs∪ {{y ∈ A | y is PRO or OPP}};
21 else
22 call is-accepted(A);
23 if pr f s 6= φ then
24 x is credulously proved by prf s;
25 else
26 x is not credulously acceptable;
27 procedure is-accepted(A)
28 let C
2
∈ {true, false};
29 foreach y ∈ A : y is MUST-OUT do
30 C
2
← false;
31 foreach (z,y) ∈ R : z ∈ A is unlabeled do
32 A
′
← A;
33 label z ∈ A
′
PRO;
34 foreach (z,u) ∈ R do
35 if u ∈ A
′
is MUST-OUT then
36 label u ∈ A
′
OPP;
37 else
38 if u ∈ A
′
is not OPP then
39 label u ∈ A
′
OUT;
40 foreach (v,z) ∈ R do
41 if v ∈ A
′
is IGNO or unlabeled then
42 label v ∈ A
′
MUST-OUT;
43 else
44 if v ∈ A
′
is OUT then
45 label v ∈ A
′
OPP;
46 if is-accepted(A
′
) = true then
47 C
2
← true;
48 else
49 label z ∈ A IGNO;
50 if C
2
=false then
51 return false;
52 if 6 ∃y ∈ A : y is MUST-OUT then
53 pr fs ← pr fs∪ {{y ∈ A | y is PRO or OPP}};
54 return true;
55 return false;
56 end procedure
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
36

Figure 3: Deciding the credulous proofs for the argument x by using algorithm 2.
ment x can be fulfilled by any admissible set contain-
ing x provided that there does not exist a preferred ex-
tension that does not contain x. Algorithm 3 decides
the skeptical acceptance of an argument x. Firstly, al-
gorithm 3 looks for a credulously accepted argument
that attacks x. If there exists such attacker then algo-
rithm 3 concludes that x is not skeptically accepted.
Otherwise, algorithm 3 searches for a preferred ex-
tension that expels x. If such an extension is found
then x is not skeptically accepted, or else x is skepti-
cally accepted provided that x is in an admissible set
S, and subsequently, S forms the skeptical proof of
x. In more details, algorithm 3 uses four labels: IN,
OUT, MUST-OUT and IGNO (short for IGNORED).
An argument y is labeled IN to indicate that y might be
in an admissible set. An argument y is labeled OUT
iff y is attacked by an IN argument. An argument y
is labeled MUST-OUT iff y attacks an IN argument.
The IGNO label designates arguments which might
not be included in a preferred extension because they
might not be defended by any IN argument. The pre-
cise usage is formalised in algorithm 3. Basically, al-
gorithm 3 repeatedly labels arguments by using the
four labels until no argument is unlabeled. Next, if
there does not exist a MUST-OUT argument then the
IN arguments make up an admissible set S. There-
after, S represents a preferred extension iff S is not
a subset of any previously decided preferred exten-
sion. At this stage if the argument in question is not
IN then the argument is not skeptically accepted. Al-
gorithm 3 is somewhat self-explanatory. However,
see figure 4 that shows how the algorithm works in
deciding the skeptically accepted argument w in the
argument system depicted in figure 1. To prove al-
gorithm 3 we have to show three issues. Firstly, the
IN arguments make up an admissible set iff no argu-
ment is MUST-OUT. Secondly, a decided admissible
set is a preferred extension iff the set is not a subset of
any previously decided preferred extension. Thirdly,
if the algorithm decides that the argument in question
is skeptically accepted then the algorithm have defi-
nitely examined all preferred extensions.
Proposition 2. Let (A,R) be an argument system and
x ∈ A. Then algorithm 3 decides that x is skeptically
accepted iff x is in every preferred extension.
Proof: Firstly, we demonstrate the admissibility of
t (see line 37). To establish that t is conflict free, as-
sume that ∃z,y ∈ t : (z,y) ∈ R, and thus, y is OUT
according to algorithm 3, see line 23. This contra-
dicts with the fact that ∀y ∈ t : y is IN, see line 37.
To show that ∀y ∈ t : y is acceptable to t, suppose
that ∃y ∈ t : ∃(z,y) ∈ R∧ 6 ∃w ∈ t : (w, z) ∈ R, and so,
z is MUST-OUT according to line 29. This contra-
dicts with the fact that t is reported as admissible iff
6 ∃w ∈ A : w is MUST-OUT, see line 36. Secondly we
AlgorithmsforAcceptanceinArgumentSystems
37

need to prove the maximality (w.r.t ⊆) of the decided
preferred extensions, i.e. members of E, see lines 38
and 39. Assume that ∃S
1
∈ E : S
1
is not maximal, and
so, there exists an admissible set S
2
6∈ E and S
2
⊇ S
1
,
i.e. ∃y ∈ S
2
: y 6∈ S
1
. This contradicts with the fact
that algorithm 3 firstly labels y IN (line 21) and then
later IGNO (line 33), and therefore, S
2
will be dis-
covered first and subsequently S
2
must be added to E
before S
1
according to lines 38 and 39. Lastly, it fol-
lows directly that algorithm 3 considers all preferred
extensions in deciding the skeptical acceptance. Note
that algorithm 3 examines all subsets of A by labeling
every argument y IN (line 21) and afterwards IGNO
(line 33) which reflects the exploration of all subsets
that include, respectively exclude, y. ■
4 THE ADVANTAGE
4.1 Over the Algorithms of Cayrol et al.
We start by highlighting the main reason behind the
speedup attained by algorithm 1 in contrast to the al-
gorithm of (Cayrol et al., 2003) (abbreviated by CAY-
Cred) for the decision problem of credulous accep-
tance. Notice that CAYCred makes use of three la-
bels: PRO, OPP and OUT. We use PRO/OPP in the
same way CAYCred does. However, CAYCred la-
bels an argument x OUT on three occasions. First,
if x is attacked by a PRO argument. Second, if x at-
tacks a PRO argument. Third, if x cannot be in an
admissible set with the current PRO arguments. As
we demonstrate, it is more efficient to use a differ-
ent label on each distinct occasion. This is exactly
what our approach does where we put in service OUT
on the first occasion, MUST-OUT on the second oc-
casion and IGNO on the third occasion. To see the
profit of our labeling scheme consider the following.
CAYCred decides that the argument in question
is not credulously accepted iff three conditions alto-
gether hold. First, there is an argument x that attacks
a PRO argument. Second, x is not attacked by a PRO
argument. Third, for every argument z that attacks
x, z is OUT. Conversely, algorithm 1 decides that the
argument in question is not credulously accepted iff
there exists a MUST-OUT argument y s.t. for every
argument w that attacks y, w is OPP, IGNO, OUT or
MUST-OUT. Therefore, the burden of work incurred
by algorithm 1 is lighter than of that induced by CAY-
Cred. In particular, the use of the MUST-OUT label
eliminates the need to look into the first condition, re-
call that by definition a MUST-OUT argument attacks
a PRO argument. Also, the labels OUT and OPP cut
Algorithm 3: Deciding the skeptical proof of an ar-
gument x in an argument system (A,R).
1 let E denote a set of preferred extensions of (A,R);
2 E ← φ;
3 if 6 ∃(y, x) ∈ R then
4 x is skeptically proved by {x};
5 exit;
6 foreach (y, x) ∈ R do
7 A
′
← A;
8 invoke algorithm 1 passing on A
′
,R and y;
9 if algorithm 1 decided that y is accepted then
10 x is not skeptically accepted;
11 exit;
12 call decide-skeptical-acceptance(A,x);
13 if E 6= φ then
14 x is skeptically proved by E;
15 exit;
16 procedure decide-skeptical-acceptance(A,x)
17 let C ∈ {true, false};
18 foreach y ∈ A : y is unlabeled do
19 C ← true;
20 A
′
← A;
21 label y ∈ A
′
IN;
22 foreach (y,z) ∈ R do
23 label z ∈ A
′
OUT;
24 foreach (z, y) ∈ R do
25 if (y, z) ∈ R then
26 C ← false;
27 else
28 if z ∈ A
′
is IGNO or unlabeled then
29 label z ∈ A
′
MUST-OUT;
30 C ← false;
31 call decide-skeptical-acceptance(A
′
,x);
32 if C = false then
33 label y ∈ A IGNO;
34 else
35 A ← A
′
;
36 if 6 ∃y ∈ A : y is MUST-OUT then
37 t ← {y ∈ A | y is IN};
38 if 6 ∃m ∈ E : t ⊆ m then
39 E ← E ∪{t};
40 if x ∈ A is not IN then
41 E ← φ;
42 x is not skeptically accepted;
43 terminate and exit;
44 end procedure
off the validation of the second condition since they
both identify an argument that is attacked by a PRO
argument. Observe that the objective of the IGNO
label is to discriminate, and subsequently to avoid,
those arguments that previously failed to be in an ad-
missible set with the current PRO arguments. Indeed,
the merit of the IGNO label is also captured by CAY-
Cred through the OUT label.
Concerning the decision problem of skeptical ac-
ceptance, the idea of the algorithm of (Cayrol et al.,
2003) (CAYSkep for short) is based on an argument x
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
38

Figure 4: Deciding the skeptical acceptance of the argument w by using algorithm 3.
not being skeptically accepted if (1) x is attacked by a
credulously accepted argument z (where z is decided
by using CAYCred), or (2) there exists an admissible
set that does not contain x and cannot be expanded
into one that contains it. Otherwise, x is skeptically
accepted iff there exists an admissible set that con-
tains x. Regarding (1), we commented earlier about
the efficiency of CAYCred in comparison with algo-
rithm 1. In deciding (2), CAYSkep uses two labels IN
and OUT, and so, an argument y is labeled IN to indi-
cate that y might be in an admissible set. The usage
of the OUT label is described earlier in the discussion
on CAYCred. To check whether S ⊆ A is an admissi-
ble set that can be expanded into one that contains the
argument in question or not, CAYSkep verifies that S
is maximally admissible w.r.t. all IN/OUT arguments.
Such verification is relatively expensive, and thus, it
is completely avoided by algorithm 3. Recall that al-
gorithm 3 decides that an admissible set is maximal
iff the set is not a subset of any previously decided
preferred extension.
4.2 Over the Algorithms of Thang et al.
The algorithm of (Thang et al., 2009) (abbreviated by
ThCred) for the decision problem of credulous accep-
tance is based on classifying arguments into four sets:
P, O, SP and SO. As an initial step, the argument in
question is added to SP and P while O and SO are
empty. Next, the following three operations are ap-
plied iteratively s.t. in every iteration one or more
tuples of (P,O,SP,SO) might be generated. First op-
eration, if ∃x ∈ P s.t. 6 ∃z ∈ SP : z attacks x then x is
dropped from P and ∀(y,x) ∈ R : y is added to O iff
y /∈ SO. Second operation, an argument x is added to
SP and P iff ∃y ∈ O : x attacks y, x /∈ O and x /∈ SO.
Third operation, an argument y is moved from O to
SO indicating that there exists an argument x ∈ SP
s.t. x attacks y. Hence, ThCred at any time might
have more than one tuple of (P,O,SP,SO). This re-
flects that ThCred explores the admissibility of differ-
ent subsets of A. ThCred reports that the argument
in question has credulous acceptance iff there exists a
tuple (P,O,SP,SO) s.t. P and O are both empty. Oth-
erwise, the argument is not credulously accepted. To
compare with algorithm 1, we stress two issues.
Firstly, ThCred algorithm might reconsider an ar-
gument x to be added to SP and P although x already
failed to be in an admissible set. Recall that algo-
rithm 1 utilizes the IGNO label to designate an argu-
ment x that is failed to be in an admissible set, and so,
x is avoided in future computations.
Secondly, ThCred might add arguments to O de-
spite they are attacked by arguments in SP. This even-
tually might waste time because ThCred unnecessar-
ily might try further arguments to be added to SP and
P to counter the newly added arguments to O. In al-
gorithm 1, this situation is avoided by using the OUT
AlgorithmsforAcceptanceinArgumentSystems
39

label s.t. as soon as an argument x is labeled PRO,
every argument that is attacked by x will be labeled
OUT. Recall that algorithm 1 explores MUST-OUT
arguments, whereas OUT arguments are disregarded
because simply they are attacked by a PRO argument.
Regarding the skeptical acceptance, the algorithm
of (Thang et al., 2009) (ThSkep for short) firstly finds,
by using a similar procedure to the one used in Th-
Cred, a set of admissible sets β = {S
1
,S
2
,...,S
n
} s.t.
∀S ∈ β, S contains the concerned argumentx. Now, let
Cβ = {S | ∃e ∈ S
1
× S
2
× ...× S
n
and S is the set of ar-
guments appearing in e} and let χβ = {S | S ∈ Cβ and
S is minimal in Cβ w.r.t. set inclusion}. Then, β rep-
resents the skeptical proof of x iff ∀S ∈ χβ there does
not exist an admissible set of arguments that attack
every argument in S. Observe that the performance
of ThSkep is bounded to the performance of ThCred
since ThSkep depends on ThCred in searching for ad-
missible sets. Furthermore, building χβ might be time
consuming and fortunately such χβ is not needed by
algorithm 3.
4.3 Over the Algorithm of Verheij
(Verheij, 2007) presented an algorithm for the cred-
ulous acceptance problem. (Verheij, 2007) classifies
arguments into two sets J and D. Initially, the argu-
ment in question is added to J. Then, two functions
are repeatedly executed on every pair of (J, D). The
first function is ExtendByAttack((J,D)) ≡ {(J,D
′
) |
D
′
is the set D extended with all arguments at-
tacking arguments in J}. The second function is
ExtendByDefence((J,D)) ≡ {(J
′
,D) | J
′
is a conflict
free, minimal set of arguments ⊇ J, s.t. ∀y ∈ D,∃x ∈
J
′
:x attacks y}. Next, if there exists (J
′
,D
′
) and (J, D)
such that J
′
= J and D
′
= D then the argument in
question is credulously proved by (J
′
,D
′
). If no new
pair (J
′
,D
′
) is produced from applying the two func-
tions on all pairs of (J,D) then the argument is not
accepted. To evaluate the performance of (Verheij,
2007) in contrast to algorithm 1 we consider three ef-
ficiency matters.
Firstly, notice the price of finding a minimal de-
fense set J
′
in ExtendByDefence. This is totally by-
passed by algorithm 1.
Secondly, (Verheij, 2007) might extend D by
adding superfluously arguments that are attacked by
arguments in J. This might worsen the efficiency
of computing J
′
where more arguments in D might
lead to more possible defense sets, and consequently,
finding a minimal defense set J
′
would be more diffi-
cult. In algorithm 1 this situation is handled by using
the OUT label designating arguments that attacked by
PRO arguments, and thus no further action is taken
regarding the OUT arguments.
Thirdly, (Verheij, 2007) might extend J by adding
arguments that already failed to form an admissible
set with the same arguments in J. Perceive that algo-
rithm 1 takes advantage of the IGNO label to charac-
terize the arguments that can not make up an admissi-
ble set with the PRO arguments. Consequently,IGNO
arguments will not be re-examined later.
5 EMPIRICAL EVALUATION
We conducted experiments to show the efficiency of
the new algorithms in comparison with the existing
algorithms of (Cayrol et al., 2003; Thang et al., 2009;
Verheij, 2007). All algorithms, new and previous
ones, were implemented in C++ on a Fedora (re-
lease 13) based machine with 4 processors (Intel core
i5-750 2.67GHz) and 16GB of memory. We tested
all implementations on 100,000 synthesized argument
systems. Algorithm 4 describes how we generated in-
stances of (A,R).
Algorithm 4: Synthesizing an instance of (A,R).
1 let A be {a
1
,a
2
...a
n
} while R is initially empty;
2 pick a random integer γ between 1 and n;
3 foreach i : 1 ≤ i ≤ n do
4 pick a random integer ε between 0 and γ-1;
5 foreach k : 1 ≤ k ≤ ε do
6 pick a random integer j between 1 and n such
that j 6= i and (a
i
,a
j
) /∈ R;
7 R ← R∪ {(a
i
,a
j
)};
To compare between algorithms we tracked the
average of elapsed time in milliseconds, denoted by
α
time
. The elapsed time was obtained by using the
time command of Linux. In addition, we reported the
average of the processed attacks, denoted by α
attacks
.
Each measurement of α
time
or α
attacks
represents the
average for 100 synthesized argument systems where
each system might have a different |R|. Coming to
the results of our experiments, tables 1, 2, 3, 4 and
5 suggest that our algorithms are more efficient than
the algorithms of (Cayrol et al., 2003), (Thang et al.,
2009) and (Verheij, 2007).
6 CONCLUSIONS
We presented novel algorithms that decide credulous
and skeptical acceptance in argument systems under
preferred semantics. An added feature of the devel-
oped algorithms is the production of proofs as to why
an argument is accepted. We have shown, analytically
and empirically, that our algorithms are more efficient
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
40

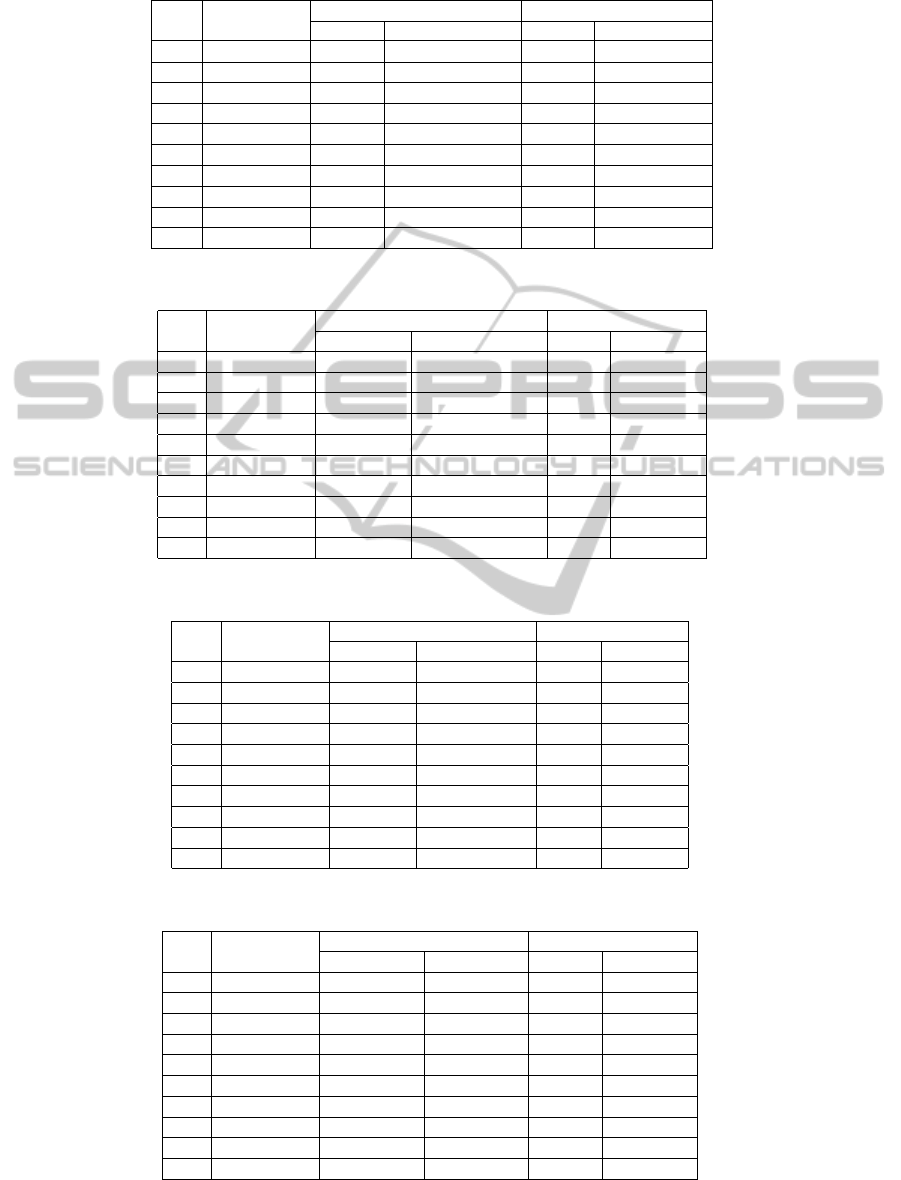
Table 1: Algorithm of Cayrol et al. for credulous acceptance versus algorithm 1.
|A| range of |R|
Algorithm of Cayrol et al. Algorithm 1
α
time
α
attacks
α
time
α
attacks
55 0-1628 52.73 1,063,995.77 34.24 99,802.83
60 0-1806 65.90 1,706,162.51 42.80 150,871.59
65 0-2181 94.90 2,999,254.36 42.90 276,545.50
70 29-2684 124.00 4,644,323.04 53.90 418,120.46
75 35-2985 166.40 6,962,249.29 79.40 655,362.79
80 71-3340 238.60 10,876,566.62 95.00 1,162,570.71
85 0-4010 354.40 16,348,586.35 116.80 1,670,378.99
90 0-4225 552.70 26,783,438.93 227.90 3,423,606.14
95 0-4396 753.80 36,771,016.57 284.00 4,164,752.18
100 0-5247 992.10 51,614,064.30 382.40 6,484,390.90
Table 2: Algorithm of Cayrol et al. for skeptical acceptance versus algorithm 3.
|A| range of |R|
Algorithm of Cayrol et al. Algorithm 3
α
time
α
attacks
α
time
α
attacks
16 0-136 31.92 360,511.44 10.30 3,642.60
17 0-149 85.20 1,426,748.62 11.40 6,880.36
18 0-198 107.70 1,803,479.38 11.90 10,251.06
19 0-225 228.20 4,819,617.69 20.70 12,506.02
20 0-227 659.40 14,253,964.92 13.30 13,292.21
21 0-258 1,759.50 38,644,605.11 15.80 20,993.86
22 0-293 3,063.20 64,765,760.79 20.90 49,025.03
23 0-295 3,555.40 81,464,211.88 19.00 35,766.54
24 0-341 19,186.50 467,335,689.25 20.70 41,515.10
25 0-347 26,175.80 629,941,785.57 36.60 83,291.68
Table 3: Algorithm of Thang et al. for credulous acceptance versus algorithm 1.
|A| range of |R|
Algorithm of Thang et al. Algorithm 1
α
time
α
attacks
α
time
α
attacks
26 0-377 69.60 96,267.14 10.20 2,964.68
27 0-414 89.90 143,211.54 11.20 3,179.99
28 0-457 164.70 235,866.67 17.60 4,004.44
29 0-508 247.30 400,605.01 10.20 4,629.05
30 0-528 264.00 401,924.72 10.70 4,772.40
31 0-519 506.30 790,854.54 13.70 6,156.54
32 0-575 613.80 943,706.04 10.40 6,767.79
33 0-605 1,124.00 1,699,251.47 10.70 8,922.32
34 0-612 1,947.90 2,647,033.75 16.70 9,004.90
35 0-656 2,737.30 3,703,646.87 11.30 9,739.63
Table 4: Algorithm of Thang et al. for skeptical acceptance versus algorithm 3.
|A| range of |R|
Algorithm of Thang et al. Algorithm 3
α
time
α
attacks
α
time
α
attacks
16 0-149 366.77 19,897.94 15.96 4,141.30
17 0-169 718.40 28,197.07 15.30 7,160.17
18 0-170 1,595.40 35,397.57 16.90 8,859.73
19 0-200 3,035.70 61,145.07 14.90 8,954.54
20 0-215 6,663.20 99,240.08 20.50 15,143.07
21 0-213 12,999.10 113,917.80 14.80 28,347.93
22 0-250 28,275.80 176,637.44 17.20 37,094.91
23 0-303 64,740.90 275,146.76 20.30 39,177.88
24 0-318 135,746.90 397,557.12 23.30 50,958.40
25 0-339 335,508.50 718,562.22 116.70 87,982.88
AlgorithmsforAcceptanceinArgumentSystems
41

Table 5: Algorithm of Verheij for credulous acceptance versus algorithm 1.
|A| range of |R|
Algorithm of Verheij Algorithm 1
α
time
α
attacks
α
time
α
attacks
21 0-235 47.58 197,363.02 10.81 1,344.26
22 0-278 60.20 278,843.87 10.00 1,359.26
23 0-278 109.70 525,903.56 10.20 1,806.13
24 0-341 166.90 835,953.03 10.30 2,170.61
25 0-386 222.10 1,121,707.65 10.20 2,469.70
26 0-391 465.00 2,323,284.54 10.20 3,027.14
27 0-403 567.30 2,790,416.39 16.80 3,143.34
28 0-447 822.00 4,121,119.53 16.60 3,818.31
29 0-471 1,757.70 8,299,326.73 13.50 4,223.32
30 0-469 2,597.50 11,474,687.66 17.60 4,843.17
than the existing algorithms of (Cayrol et al., 2003;
Thang et al., 2009; Verheij, 2007). We plan to invest
our algorithms in extended models of Dung’s system
such as the value based argument systems of (Bench-
Capon, 2003) and varied strength attacks systems of
(Martinez et al., 2008). Likewise, our work could
be expanded to handle other argumentation semantics
such as the ideal semantics (Dung et al., 2007) and the
stage semantics (Verheij, 1996). A further perspective
of this work is to examine heuristics that boosts the
efficiency of the developed algorithms. Particularly,
recall that the algorithms arbitrarily select unlabeled
arguments for labeling, and hence, we intend to study
different criteria for argument selection.
Some authors call the algorithms that yield proofs
’dialectical proof procedures’ referring to the fact that
a proof of an accepted argument might be, roughly,
defined by the arguments put forward during a dia-
log between two parties. In fact, argumentation se-
mantics can be defined by using the dialog notion
(see e.g. (Jakobovits and Vermeir, 1999; Vreeswijk
and Prakken, 2000; Dunne and Bench-Capon, 2003;
Modgil, 2009)). Hence, (Cayrol et al., 2003) de-
scribe dialogs for preferred semantics as a means for
presenting their algorithms. However, (Thang et al.,
2009) make use of so called ’dispute trees’ to pave
the way for introducing their algorithms, while (Ver-
heij, 2007) presented his algorithm by employing the
notion of ’labellings’ rather than specifying formal
dialogs. Furthermore, argument-based dialogs have
been extensively studied as a backbone for interac-
tions between agents in multi-agent systems, see e.g.
(McBurney and Parsons, 2009) for an overview.
Broadly, there are several works on computing de-
cision problems in argument systems. To the best of
our knowledge the algorithms of (Cayrol et al., 2003;
Thang et al., 2009; Verheij, 2007) are the only re-
lated ones to the algorithms presented in this paper
where all of them, including our algorithms, are iden-
tified by two characteristics. Firstly, all of the algo-
rithms decide acceptance without literally enumerat-
ing all preferred extensions. Secondly, all of the al-
gorithms produce proofs for the accepted arguments.
However, in this context it is noteworthy to mention
that (Vreeswijk, 2006) showed algorithmically how
importance to decide all minimally admissible sets
while (Doutre and Mengin, 2004) specify dialogs for
skeptical proofs under preferred semantics. For the
problem of extension enumeration, the algorithms of
(Doutre and Mengin, 2001; Modgil and Caminada,
2009; Dvor´ak et al., 2012; Nofal et al., 2012) are ded-
icated to finding all preferred extensions while the al-
gorithms of (Caminada, 2007; Caminada, 2010) find
semi stable, respectively stage, extensions. Another
line of research concerns encoding decision problems
of argument systems into other formalisms and then
solving them by using a respective solver see for ex-
ample (Besnard and Doutre, 2004; Nieveset al., 2008;
Egly et al., 2008; Amgoud and Devred, 2011; Dvorak
et al., 2012). The work of (Li et al., 2011) examines
approximation versus exact computations in the con-
text of argument systems, whereas the experiments of
(Baumann et al., 2011) evaluate the effect of splitting
an argument system on the computation of preferred
extensions. The work of (Liao et al., 2011) shows
how to partially reevaluate the status of arguments if
A or R change. From a computational theoretical per-
spective, the decision problems of skeptical and cred-
ulous acceptance under preferred semantics are likely
to be intractable, see e.g. (Dimopoulos et al., 2000;
Dunne, 2007; Ordyniak and Szeider, 2011). Finally,
there are several implemented tools in the context of
argument systems such as (Gaertner and Toni, 2007;
South et al., 2008).
REFERENCES
Amgoud, L. and Devred, C. (2011). Argumentation frame-
works as constraint satisfaction problems. In SUM,
pages 110–122.
Amgoud, L. and Prade, H. (2009). Using arguments for
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
42

making and explaining decisions. Artificial Intelli-
gence Journal, 173:413–436.
Baroni, P., Caminada, M., and Giacomin, M. (2011). An
introduction to argumentation semantics. The Knowl-
edge Engineering Review, 26(4):365–410.
Baumann, R., Brewka, G., and Wong, R. (2011). Splitting
argumentation frameworks: An empirical evaluation.
In TAFA, pages 17–31.
Bench-Capon, T. (2003). Persuasion in practical argument
using value-based argumentation frameworks. Logic
and Computation, 13(3):429–448.
Besnard, P. and Doutre, S. (2004). Checking the acceptabil-
ity of a set of arguments. In NMR, pages 59–64.
Caminada, M. (2007). An algorithm for computing semi-
stable semantics. In ECSQARU, pages 222 – 234.
Caminada, M. (2010). An algorithm for stage semantics. In
COMMA, pages 147–158.
Cayrol, C., Doutre, S., and Mengin, J. (2003). On deci-
sion problems related to the preferred semantics for
argumentation frameworks. Logic and Computation,
13(3):377–403.
Dimopoulos, Y., Nebel, B., and Toni, F. (2000). Finding
admissible and preferred arguments can be very hard.
In KR, pages 53–61.
Doutre, S. and Mengin, J. (2001). Preferred extensions
of argumentation frameworks: Query, answering, and
computation. In IJCAR, pages 272–288.
Doutre, S. and Mengin, J. (2004). On sceptical versus cred-
ulous acceptance for abstract argument systems. In
JELIA, pages 462–473.
Dung, P. (1995). On the acceptability of arguments and its
fundamental role in non monotonic reasoning, logic
programming and n-person games. Artificial Intelli-
gence, 77(2):321–357.
Dung, P., Mancarella, P., and Toni, F. (2007). Computing
ideal skeptical argumentation. Artificial Intelligence,
171(10-15):642–674.
Dunne, P. (2007). Computational properties of argument
systems satisfying graph-theoretic constraints. Artifi-
cial Intelligence, 171:701–729.
Dunne, P. E. and Bench-Capon, T. J. M. (2003). Two
party immediate response disputes: Properties and ef-
ficiency. Artificial Intelligence, 149(2):221–250.
Dvorak, W., Jarvisalo, M., Wallner, J., and Woltran, S.
(2012). Complexity-sensitive decision procedures for
abstract argumentation. In KR.
Dvor´ak, W., Pichler, R., and Woltran, S. (2012). Towards
fixed-parameter tractable algorithms for abstract argu-
mentation. Artificial Intelligence, 186:1–37.
Egly, U., Gaggl, S. A., and Woltran, S. (2008). Aspar-
tix: Implementing argumentation frameworks using
answer-set programming. In ICLP, pages 734–738.
Gaertner, D. and Toni, F. (2007). Casapi: a system for cred-
ulous and sceptical argumentation. In NMR, pages 80–
95.
Jakobovits, H. and Vermeir, D. (1999). Dialectic semantics
for argumentation frameworks. In ICAIL, pages 53–
62.
Li, H., Oren, N., and Norman, T. (2011). Probabilistic ar-
gumentation frameworks. In TAFA, pages 1–16.
Liao, B. S., Jin, L., and Koons, R. C. (2011). Dynamics
of argumentation systems: A division-based method.
Artif. Intell., 175(11):1790–1814.
Martinez, D., Garcia, A., and Simari, G. (2008). An ab-
stract argumentation framework with varied-strength
attacks. In KR, pages 135–143.
McBurney, P. and Parsons, S. (2009). Dialogue games for
agent argumentation. In Simari, G. and Rahwan, I.,
editors, Argumentation in Artificial Intelligence, pages
261–280. Springer.
Modgil, S. (2009). Labellings and games for extended ar-
gumentation frameworks. In IJCAI, pages 873–878.
Modgil, S. and Caminada, M. (2009). Proof theories and
algorithms for abstract argumentation frameworks. In
Rahwan, I. and Simari, G. R., editors, Argumentation
in AI, pages 105–129. Springer.
Mozina, M., Zabkar, J., and Bratko, I. (2007). Argu-
ment based machine learning. Artificial Intelligence,
171:922–937.
Nieves, J., Cortes, U., and Osorio, M. (2008). Preferred
extensions as stable models. Theory and Practice of
Logic Programming, 8(4):527–543.
Nofal, S., Dunne, P., and Atkinson, K. (2012). On preferred
extension enumeration in abstract argumentation. In
COMMA, to appear.
Ordyniak, S. and Szeider, S. (2011). Augmenting tractable
fragments of abstract argumentation. In IJCAI, pages
1033–1038.
South, M., Vreeswijk, G., and Fox, J. (2008). Dungine: A
java dung reasoner. In COMMA, pages 360–368.
Thang, P., Dung, P., and Hung, N. (2009). Towards a com-
mon framework for dialectical proof procedures in ab-
stract argumentation. Logic and Computation, pages
1071–1109.
Verheij, B. (1996). Two approaches to dialectical argumen-
tation: admissible sets and argumentation stages. In
The Eighth Dutch Conference on AI, pages 357–368.
Verheij, B. (2007). A labeling approach to the computation
of credulous acceptance in argumentation. In IJCAI,
pages 623–628.
Vreeswijk, G. (2006). An algorithm to compute minimally
grounded and admissible defence sets in argument
systems. In COMMA, pages 109–120.
Vreeswijk, G. and Prakken, H. (2000). Credulous and
sceptical argument games for preferred semantics. In
JELIA, pages 239–253.
AlgorithmsforAcceptanceinArgumentSystems
43