
Facial Landmarks Localization Estimation by Cascaded Boosted
Regression
Louis Chevallier
1
, Jean-Ronan Vigouroux
1
, Alix Goguey
1,2
and Alexey Ozerov
1
1
Technicolor, Cesson-S
´
evign
´
e, France
2
Ensimag, Saint-Martin d’H
`
eres, France
Keywords:
Face Landmarks Localization, Boosted Regression.
Abstract:
Accurate detection of facial landmarks is very important for many applications like face recognition or analy-
sis. In this paper we describe an efficient detector of facial landmarks based on a cascade of boosted regressors
of arbitrary number of levels. We define as many regressors as landmarks and we train them separately. We
describe how the training is conducted for the series of regressors by supplying training samples centered on
the predictions of the previous levels. We employ gradient boosted regression and evaluate three different
kinds of weak elementary regressors, each one based on Haar features: non parametric regressors, simple lin-
ear regressors and gradient boosted trees. We discuss trade-offs between the number of levels and the number
of weak regressors for optimal detection speed. Experiments performed on three datasets suggest that our
approach is competitive compared to state-of-the art systems regarding precision, speed as well as stability of
the prediction on video streams.
1 INTRODUCTION
Facial landmarks detection is an important step in
face analysis. Indeed, performance of face recogni-
tion or characterization systems (Everingham et al.,
2006) greatly depends on the accuracy of this mod-
ule. Accordingly, much work has been devoted to the
problem of accurate and robust localization of facial
landmarks. The importance of the required accuracy
level depends on the final application. For example,
for applications requiring a fine analysis of faces like
lips-reading, a very precise localization of landmarks
is needed. Typically, such high precision performance
is required on near frontal faces; non-frontal positions
are less likely to be subjected to these analyzes. More-
over, when this analysis involves motion video, tem-
poral stability at a given precision rate is useful.
Most of state of the art landmark detectors (Cootes
et al., 2001; U
ˇ
ri
ˇ
c
´
a
ˇ
r et al., 2012; Cao et al., 2012;
Dantone et al., 2012; Vukadinovic and Pantic, 2005)
are formulated as optimization or regression prob-
lems in some high-dimensional space (e.g., dozens
of thousands of features). Thus, the precision of
these approaches is limited by feature resolution. Us-
ing higher feature resolution (i.e., a feature space
of much higher dimension), will in general not lead
to improved precision due to limited training data,
but instead entail over-fitting problems. We pro-
pose a new approach that allows increased feature
resolution while keeping the feature space dimen-
sion unchanged, leading to higher landmark detec-
tion accuracy. This is achieved by using a cascade
of boosted regressors, where the features used at each
cascade level are extracted from a restricted area sur-
rounding the corresponding landmark estimated by
the previous levels of the cascade. We also discuss
trade-offs between the number of cascades and the
number of weak regressors for an optimal detection
speed/precision ratio.
Our main contributions are:
1. A fast and accurate landmark position estimation
algorithm, based on boosted weak regressors and
Haar features extracted from the surrounding area,
and a cascaded estimation scheme iterating on
narrowing areas around each landmark.
2. A comprehensive assessment of the proposed
estimator with regards to standard benchmarks,
databases and state of the art landmark estima-
tors, including an evaluation of its spatial stabil-
ity. This is a new feature to our knowledge which
is of great importance for the applications we are
considering.
3. The flexibility of the proposed approach allows
adjustment of the accuracy vs. computational load
513
Chevallier L., Vigouroux J., Goguey A. and Ozerov A..
Facial Landmarks Localization Estimation by Cascaded Boosted Regression.
DOI: 10.5220/0004192705130519
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 513-519
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

by simply varying the number of cascades.
The paper is organized as follows: related work and
the proposed approach are described respectively in
sections 2 and 3. Sections 4 and 5 are devoted to eval-
uation of performance and temporal stability. Some
conclusions are drawn in section 6.
2 RELATED WORK
The problem of predicting the location of facial
landmarks consists in estimating the vector S =
[x
1
, y
1
, ...x
i
, y
i
, x
N
, y
N
]
T
comprising N pairs of 2D co-
ordinates based on the appearance of the face. To
minimize ||S −
ˆ
S||
2
, where
ˆ
S denotes an estimate,
most of the existing approaches use optimization
techniques (Cristinacce and Cootes, 2008; U
ˇ
ri
ˇ
c
´
a
ˇ
r
et al., 2012) where the prediction is obtained as a
solution of some optimization criterion, or regres-
sion techniques (Dantone et al., 2012; Valstar et al.,
2010) where a function directly produces the predic-
tion. Our approach follows the second direction.
Regarding data modeling, most approaches rely
on both shape modeling representing a priori knowl-
edge about landmarks locations and texture model-
ing corresponding to values of pixels surrounding the
landmarks in the image itself, i.e., the posterior obser-
vations.
Active Shape Models (ASM) (Cootes et al., 1995)
is a popular hybrid approach that uses a statistical
model describing the shape (set of landmarks) of
faces together with models of the appearance (tex-
ture) of landmarks. The prediction is iteratively up-
dated to fit an example of the object in a new image.
The shapes are constrained by the Point Distribution
Model (PDM) (Kass et al., 1988) to vary only in ways
seen in a training set of labeled examples. Active Ap-
pearance Models (AAM) (Cootes et al., 2001) are an
extension of the ASM approach. In AAM, a global
appearance model is used to optimize the shape pa-
rameters. Among the weaknesses frequently pointed
out for this approach are the need for images of suf-
ficiently high resolution, and the sensitivity to initial-
ization. Our regression approach using Haar features
computed over the face area, can, on the contrary,
work with small images–in theory as small as the grid
used for defining the set of Haar features–in our case
17x17, yielding 13920 features. Moreover, as a re-
gression approach there is no iterative search process
to be initialized.
A straightforward approach to landmark detec-
tion is based on using independently trained detectors
for each facial landmark. For instance the AdaBoost
based detectors and its modifications have been fre-
quently used (Viola and Jones, 2001). If applied in-
dependently, the individual detectors often fail to pro-
vide a robust estimate of the landmark positions be-
cause of the weakness of local evidence. This can be
solved by using a prior on the geometrical configura-
tion of landmarks.
Valstar et al. (Valstar et al., 2010) proposed trans-
forming the detection problem into a regression prob-
lem. They define a regression algorithm, based on
Support Vector Regression, BoRMan, to estimate the
positions of the feature points from Haar features
computed at locations with maximum a priori prob-
abilities. A Belief Propagation algorithm is used to
improve the estimation of the target points, using a
Markov Random Field modeling the relative positions
of the points. Series of estimations are performed, by
adding Gaussian noise to the current target estimation,
and retaining the median of the predictions as the final
estimation.
In (Everingham et al., 2006), a facial landmark de-
tector is described which is based on the independent
training of a local appearance model and the deforma-
tion cost of the Deformable Part Model–a structure
which captures spatial relation between landmarks.
The former relies on an AdaBoost classifier using
Haar like features. The latter consists of a genera-
tive model using a mixture of Gaussian trees. In our
evaluation section, we use an implementation of this
system, which represents an optimization based solu-
tion to landmark detection.
Another approach based on regression for deter-
mining landmarks localization is described in (Cao
et al., 2012). In this work, explicit multiple regression
is used to directly predict landmarks localization. All
landmarks coordinates (the shape) are predicted si-
multaneously by the regressor. The design relies on a
cascaded structure: a top level boosted regressor uses
weak regressors that are themselves boosted. These
primary regressors use weak fern regressors: regres-
sion trees with a fixed number of leaves. In contrast
with this system, our system consists of as many re-
gressors as landmarks to be predicted. While (Cao
et al., 2012) described a hierarchical structure, the
structure of our system is a true cascade of regressors
similar to the classifiers cascade proposed by (Viola
and Jones, 2001) in their face detector.
3 LANDMARK POSITION
ESTIMATION BY CASCADED
BOOSTED REGRESSION
We propose to estimate the position of the landmarks
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
514

by using boosting and cascading techniques that lead
to a fast and accurate result. The prediction of the
coordinates (x, y) of each landmark is done using a
boosted regressor, based on Haar features computed
on the detected face. A more precise localization is
obtained using cascaded predictors. Each landmark
is predicted independently of the others, instead of
using a shape-based approach, as in (Lanitis et al.,
1997; Cootes et al., 2001; Cristinacce and Cootes,
2008; U
ˇ
ri
ˇ
c
´
a
ˇ
r et al., 2012), and for each landmark
the x and y coordinates are predicted independently.
Actually, even if each landmark is predicted indepen-
dently, a shape constraint is implicitly taken into ac-
count by the first regressor since the features used by
this regressor are extracted from the totality of the
face area. A final test could be made to detect and
correct grossly erroneous landmarks. We believe that
this approach is robust to partial occlusion, since vari-
ability of one landmark does not perturb the position
of the others.
In contrast to (Valstar et al., 2010) we do not
regress from different starting points, and take the me-
dian position as an estimator. We build a series of es-
timations of the positions of the landmarks, designed
to converge to the sought landmark with high preci-
sion. At each step the regressor operates on increas-
ingly narrow windows.
The image measurements used in our system are
Haar features. This choice has the advantage that inte-
gral representations of images were readily available
since they are typically required by the ubiquitous Vi-
ola and Jones face detector (Viola and Jones, 2001)
we are using. The Haar features are defined based on
a regular grid mapped on the shrinking image area to
be analyzed. We set the size of the grid to 17 × 17
cells and we use eight Haar feature shapes (see fig-
ure 1). Scaling and translating them results in a total
of 13,920 Haar features.
Figure 1: The eight Haar features used
3.1 The First Level Regressor
The first level regressor is a boosted regressor, using
the algorithms described in (Friedman, 2001).
For the clarity of presentation we consider the case
where we have only one coordinate of one landmark
to predict for each image. Let G be a set of N im-
ages, and y
i
be the coordinate of the landmark on im-
age i; the coordinates are measured in pixels from
the top-left corner of the detection box. We have at
our disposal a set of measurements (Haar features)
on each image, used by the weak regressors and we
want to create the most efficient strong predictor of
the landmark coordinate, from a linear combination
of weak predictors. Here the weak predictors consist
of least-square fitted linear predictors using Haar fea-
tures computed on the detected face (Viola and Jones,
2001).
The strong predictor is built iteratively as follows.
Let F be a matrix such that F
i j
is the value of the
feature F
j
on image i. Let Y
(n)
be a vector con-
taining the values to be predicted at iteration n. At
first step Y
(1)
is initialized to the coordinates to pre-
dict: Y
(1)
= Y , i.e., the vector of all the y
i
. We
predict Y
(n)
from F
j
using a standard linear predic-
tor:
d
Y
(n)
= a
j
F
j
+ b
j
. The prediction error is E
(n)
j
=
Y
(n)
−
d
Y
(n)
= Y
(n)
− a
j
F
j
− b
j
, and the mean error is
e
(n)
j
=
1
N
kE
(n)
j
k. The feature minimizing this error,
F
j
n
is selected as n
th
weak predictor. The predictions
are subtracted from the value to predict, with a given
weight w
n
set between 0.1 and 1, and the new value
to predict is thus:
Y
(n+1)
= Y
(n)
− w
n
(a
j
n
F
j
n
− b
j
n
).
This is iterated p times and results in a Linear strong
predictor of the form:
P
(p)
(i) =
p
∑
k=1
w
k
a
j
k
F
j
k
+ b
j
k
.
3.2 Next Regression Levels
The estimation of the position of a landmark can be
improved by using the first estimation to re-center a
window around the landmark of interest. This is the
basis of our cascading process (see figure 2.)
The prediction window on the first level is the
window detected by the face detector. In the second
and subsequent levels it is a smaller window centered
on the landmark position predicted by the previous
level. For the size of the successive windows we use
a decreasing ratio applied to the original face bound-
ing box : 1.0, 0.8, 0.6, 0.4 for the four first levels.
The levels of the cascade are therefore trained se-
quentially. The predictions of the previous level are
used to train the next level.
FacialLandmarksLocalizationEstimationbyCascadedBoostedRegression
515

Figure 2: Three successive steps of regression for the Left
Mouth Corner.
3.3 Other Weak Regressors
As an alternative to Linear predictors for weak regres-
sors we consider Non-Parametric weak-regressors. In
this case, we bin the values of each feature F
j
and we
estimate y
i
by the mean of Y for the images falling
in the same bin as F
i j
. The boosting algorithm is ap-
plied as previously on the residual. This is somewhat
equivalent to ferns (Doll
´
ar et al., 2010) using only one
feature.
We have also experimented with gradient boosted
trees (GBT) as weak regressors. Those regressors
combining many Haar features were expected to pro-
vide more expressive power. Given the number of
training image samples – ca. 5,000 – compared to
the number of features (13,920), the challenge was to
prevent over-fitting. Optimal parameters were found
through cross validation and we set the number of
trees and maximal depth so that the total number of
leaves (Haar features) were the same as in the two
previous methods. In this experiment we are using 30
Haar features per weak regressor. The training time
per landmark with 4 cascades is 8 minutes on an octo-
core 3GHz Intel processor.
We compare the merit of these three boosted weak
regressors by testing them on the BioID database (Je-
sorsky et al., 2001) using four cascades (see table 1.)
Table 1: Percentage of tested images below error threshold
on BioID dataset with three different weak regressors pre-
dicting the right of mouth corner.
Percent. of tested images 25% 50% 75%
GBT 2.2% 3.4% 5.0%
Linear 2.7% 4.2% 6.5%
Non Parametric 3.0% 4.8% 8.4%
We notice that GBT clearly outperforms the two
other approaches.
3.4 Parameters Settings
Our approach uses two important parameters for
training: the number of weak regressors and the num-
ber of cascade levels. In order to find the optimal
choice we have tested several trade-offs presented in
table 2.
Table 2: Error threshold at 50% of tested images on BioID
dataset with respect to weak regressors number and cascade
levels.
X
X
X
X
X
X
X
X
X
X
# levels
# weaks
15 30 45 60
1 0.057 0.044 0.041 0.038
2 0.047 0.039 0.036 0.034
3 0.042 0.037 0.034 0.032
4 0.040 0.037 0.033 0.032
Of course the greater the computation effort,
the lower the error, but for a given computation
load (i.e., the total number of Haar features which
is proportional to the product numberO f Weaks ×
numberO f Levels), say 90, we can see that two lev-
els and 45 weak regressors is the best choice.
4 EVALUATION OF
PERFORMANCE
4.1 Evaluation Methodology
The models trained as described in the previous sec-
tion were applied on three publicly available data sets
with a manually labeled ground truth:
1. BioID (Jesorsky et al., 2001) is a very popular
dataset containing 1,521 frontal face images with
moderate variations in light condition and pose.
2. The PUT (Kasi
´
nski et al., 2008) dataset has 9,971
faces. The main source of face appearance vari-
ations comes from changes in poses and expres-
sions .
3. The MUCT (Milborrow et al., 2010) dataset has
3,755 faces. It provides some diversity of lighting,
age and ethnicity.
The set of landmarks provided by these databases
are all different, so we retained a set of nine land-
marks found on all three datasets and for which there
is a good agreement regarding actual landmark posi-
tions: right and left corners of mouth, inner and outer
corners of eyes, nose and nostrils (see figure 3.)
Our evaluation methodology consists of training
our system with half of the images of each dataset
and testing it on the rest. We use an evaluation met-
rics proposed in (Cootes et al., 2001) and defined as
follows:
m
e
=
1
ns
n
∑
i=1
d
i
where d
i
is the Euclidean distance between the ground
truth landmark and the predicted one and s is the inter-
ocular distance. n = 9 is the number of landmarks.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
516

4.2 Results
The systems against which we benchmarked our sys-
tem are FLandmark (U
ˇ
ri
ˇ
c
´
a
ˇ
r et al., 2012), Oxford (Ev-
eringham et al., 2006), CLM (Cristinacce and Cootes,
2008), Kumar (Belhumeur et al., 2011), Valstar (Val-
star et al., 2010) and Cao (Cao et al., 2012). The IN-
RIA system is a variant of (Everingham et al., 2006)
trained with a different training dataset.
Table 3: Percentage of tested images below the average er-
ror threshold on BioID dataset.
Percent. of tested images 25% 50% 75%
FLandmark 5.4% 5.5% 7.0%
Our system 2% 2.6% 3.2%
CLM 2.5% 4.5% 6.5%
Valstar 1.5% 3% 5%
We compare our system with recent systems for
which the implementation was available
1
. For some
others, we use the figures reported in corresponding
papers on the same datasets: In the curves on figures 4
and 5 the error curve corresponds to the average error
and to the maximum error observed on all the land-
marks.
The obtained precision on PUT and MUCT im-
ages (figure 5) are not as good as on BioID (figure 4)
because the pose of faces varies much more.
5 EVALUATION OF TEMPORAL
STABILITY
5.1 Motivation
In practice, the accuracy of landmark prediction is
limited by the modeling restriction, noise in the an-
notation and inherent ambiguity of the localization of
facial landmark. 3% seems to be a performance that
will be difficult to outperform.
If a perfect accuracy cannot be reached, for some
applications, it is important that the detector be as sta-
ble as possible. For example, the output of a landmark
detector might be used as input of a speaking/non-
speaking classifier, which decides whether or not a
visible face is currently speaking. Thus, if the land-
marks are used to analyze the face (evolution of the
mouth height or width), the noise due to the predictor
should be kept as small as possible. If the accuracy
1
We did some tests with an implementation of (Valstar
et al., 2010), but it gave results very different to what was
reported in the paper, thus we do not present them.
Figure 3: The nine landmarks used for the experiments.
Figure 4: Cumulative distribution of point to point error
measure on the BioID test set.
is not good because of a constant bias, the prediction
can still be useful.
Temporal stability of landmarks prediction has
rarely been evaluated in the literature. We approach
the problem by analyzing the normalized error over
time. We propose to evaluate stability using auto-
correlation of the vectors of normalized errors corre-
sponding to landmarks estimated for each frame of a
video sequence. For this purpose, we have created our
own ground truth of annotated frames. This dataset
is comparable to the FGNET
2
database but we found
that we required more precision in the position of the
landmarks than available in the latter for our compar-
ison.
2
http://www-prima.inrialpes.fr/FGnet/data/
01-TalkingFace/talking face.html
FacialLandmarksLocalizationEstimationbyCascadedBoostedRegression
517
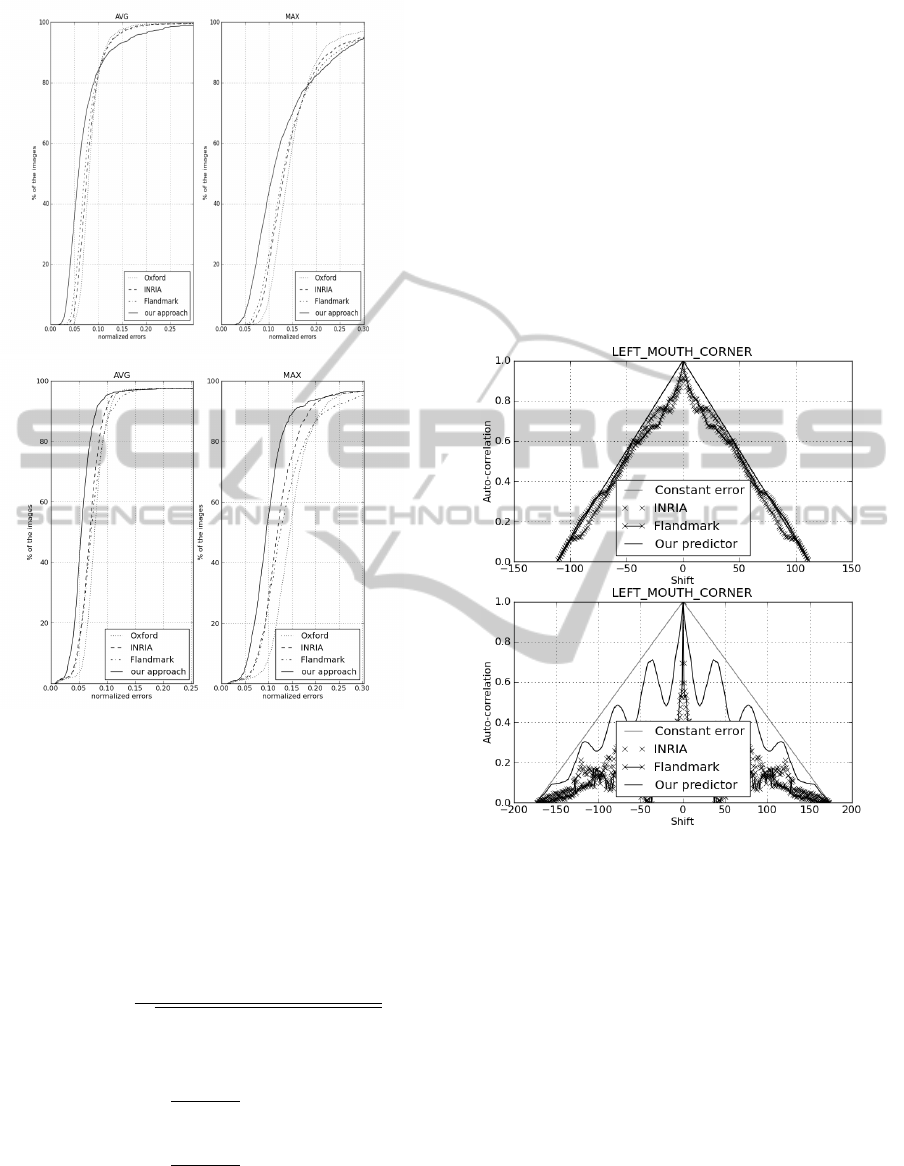
Figure 5: Cumulative distribution of point to point error
measure on the PUT and MUCT test set.
The auto-correlation vector ACor was calculated,
using function Cor, as follows. x and y are two vec-
tors and N = Card(x) = Card(y), the cardinality of
x and y. s is the shift index. Therefore, ACor(x) =
(Cor(x, x)
s
)
s∈[[1−N;N−1]]
.
Cor(x, y)
s
=
Cor
A
(x, y)
s
s ∈ A = [[0, N − 1]]
Cor
B
(x, y)
s
s ∈ B = [[1 − N, −1]]
where
Cor
A
(x, y)
s
=
∑
N−s
i=0
(x
i+s
− ¯x
s
)(y
i
− ¯y
s
)
q
∑
N
i=0
(x
i
− ¯x
s
)
2
∑
N
i=0
(y
i
− ¯y
s
)
2
and
¯x
s
=
1
2 ∗ N − s
N−s
∑
i=0
x
i+s
¯y
s
=
1
2 ∗ N − s
N−s
∑
i=0
y
i
Similarly:
Cor
B
(x, y)
s
= Cor
A
(y, x)
−s
5.2 Results
In the two graphs represented in figure 6, we plot the
auto-correlation of a constant error vector (as a base-
line) and the normalized errors vector computed by
three different detectors. The more stable a detector
is, the closer to the baseline the corresponding curves
should be.
We present here the results for two types of video
streams: one with a speaker (whose head and lips are
moving) and another with a quiet listener (who re-
mains still). In each case, we show the graph corre-
sponding to the left corner of mouth landmark error.
The results show that our system has a better stability
Figure 6: Auto-correlation of the normalized error vector of
a non-speaking video sequence (upper graph) and a speak-
ing one (lower graph).
compared to the others in both types of video streams.
The curve oscillations observed in the lower graph
of figure 6 are due to a repetitive movement of the
speaker lips. In the upper graph, the described fea-
ture does not have a repetitive pattern. This behavior
can be regarded as an illustration of the superiority of
regression techniques over optimization based tech-
niques.
6 CONCLUSIONS
We have presented a technique of cascaded regression
for direct prediction of facial landmarks. The algo-
rithm consists of predicting successive 2D locations
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
518

of the landmarks in a coarse to fine manner using a
series of cascaded predictors, conferring robustness to
the approach. Indeed predicting landmarks indepen-
dently results in high precision since failure to find the
good location of one of the landmarks does not prop-
agate to the others. The regressors at each level of the
cascade are based on gradient boosting. Three kinds
of weak regressors have been assessed: linear regres-
sors, non-parametric regressors and regression trees.
The gradient boosted trees have the best performance.
This simple scheme has proved to be very efficient
compared to other tested approaches in terms of loca-
tion errors. This approach is also very fast: it takes
8 milliseconds to compute the locations of 20 land-
marks (not counting the computation of the integral
image which is typically required for the detection of
the face).
As possible extensions of the approach, we could
consider applying a post-processing to the predicted
landmarks by enforcing shape consistency (Bel-
humeur et al., 2011). An attractive capability of our
model is to make it possible to trade precision against
speed by traversing only a suitable number of levels
of the cascade.
We believe that this generic approach could be ap-
plied to other problems involving regression where
features derive from measurements from the signal
e.g., to detection and localization of more generic ob-
jects using part based models.
ACKNOWLEDGEMENTS
This work was partially funded by the QUAERO
project supported by OSEO and by the European in-
tegrated project AXES.
REFERENCES
Belhumeur, P. N., Jacobs, D. W., Kriegman, D. J., and Ku-
mar, N. (2011). Localizing parts of faces using a con-
sensus of exemplars. In The 24th IEEE Conference on
Computer Vision and Pattern Recognition (CVPR).
Cao, X., Wei, Y., Wen, F., and Sun, J. (2012). Face aligne-
ment by explicit shape regression - to appear. In Proc.
of CVPR’12.
Cootes, T. F., Edwards, G. J., and Taylor, C. J. (2001). Ac-
tive appearance models. IEEE Transactions Pattern
Analysis and Machine Intelligence, 23(6):681–685.
Cootes, T. F., Taylor, C. J., Cooper, D. H., and Graham, J.
(1995). Active shape models – their training and ap-
plication. Computer Vision and Image Understanding,
61(1):38–59.
Cristinacce, D. and Cootes, T. (2008). Automatic feature
localisation with constrained local models. Pattern
Recognition, 41(10):3054–3067.
Dantone, M., Gall, J., Fanelli, G., and Van Gool, L. (2012).
Real-time facial feature detection using conditional
regression forests. In Computer Vision and Pattern
Recognition (CVPR).
Doll
´
ar, P., Welinder, P., and Perona, P. (2010). Cascaded
pose regression. In Computer Vision and Pattern
Recognition (CVPR), pages 1078–1085.
Everingham, M., Sivic, J., and Zisserman, A. (2006). Hello!
my name is. . . Buffy – Automatic naming of charac-
ters in TV video. In Proceedings of the British Ma-
chine Vision Conference, volume 2.
Friedman, J. H. (2001). Greedy function approximation:
A gradient boosting machine. Annals of Statistics,
29(5):1189–1232.
Jesorsky, O., Kirchberg, K. J., and Frischholz, R. (2001).
Robust Face Detection using the Hausdorff distance.
In AVBPA, pages 90–95.
Kasi
´
nski, A., Florek, A., and Schmidt, A. (2008). The PUT
face database. Image Processing and Communica-
tions, 13(3):59–64.
Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:
Active contour models. International Journal of Com-
puter Vision, 1(4):321–331.
Lanitis, A., Taylor, C. J., and Cootes, T. F. (1997). Auto-
matic interpretation and coding of face images using
flexible models. IEEE Transactions Pattern Analysis
and Machine Intelligence, 19(7):743–756.
Milborrow, S., Morkel, J., and Nicolls, F. (2010). The
MUCT Landmarked Face Database. Pattern Recog-
nition Association of South Africa.
U
ˇ
ri
ˇ
c
´
a
ˇ
r, M., Franc, V., and Hlav
´
a
ˇ
c, V. (2012). Detector of
facial landmarks learned by the structured output svm.
In Proceedings of the 7th International Conference on
Computer Vision Theory and Applications. VISAPP
’12.
Valstar, M., Martinez, B., Binefa, X., and Pantic, M. (2010).
Facial point detection using boosted regression and
graph models. In Proceedings of IEEE Int’l Conf.
Computer Vision and Pattern Recognition (CVPR’10),
pages 2729–2736, San Francisco, USA.
Viola, P. A. and Jones, M. J. (2001). Rapid object detection
using a boosted cascade of simple features. In Com-
puter Vision and Pattern Recognition (CVPR), pages
511–518.
Vukadinovic, D. and Pantic, M. (2005). Fully automatic fa-
cial feature point detection using gabor feature based
boosted classifiers. In Proceedings of IEEE Int’l
Conf. Systems, Man and Cybernetics (SMC’05), pages
1692–1698, Waikoloa, Hawaii.
FacialLandmarksLocalizationEstimationbyCascadedBoostedRegression
519
