Beat Detection Enhancing using AdaBoost
Jakub Kuzilek and Lenka Lhotska
Department of Cybernetics, FEE CTU in Prague, Technicka 2, Prague, Czech Republic
Keywords:
QRS Detection, AdaBoost, Combining Classifiers.
Abstract:
Beat detection is a basic and fundamental step in electrocardiogram (ECG) processing. In many ECG applica-
tion time is crucial and slow beat detection algorithm may cause serious problems. Beat detection algorithm
desired property is to detect sufficiently large number of QRS complexes with small error in shortest time as
possible. Our proposed method tries to combine weak and fast QRS detectors such as amplitude threshold
based detector in order to obtain better detection result with very low computational increase. We developed
a modified version of the well known AdaBoost algorithm for combining weak QRS detectors. Our algo-
rithm has been compared with the performance of our implementation of the Pan-Tompkins’s beat detection
algorithm.
1 INTRODUCTION
Beat detection is the most fundamental task in elec-
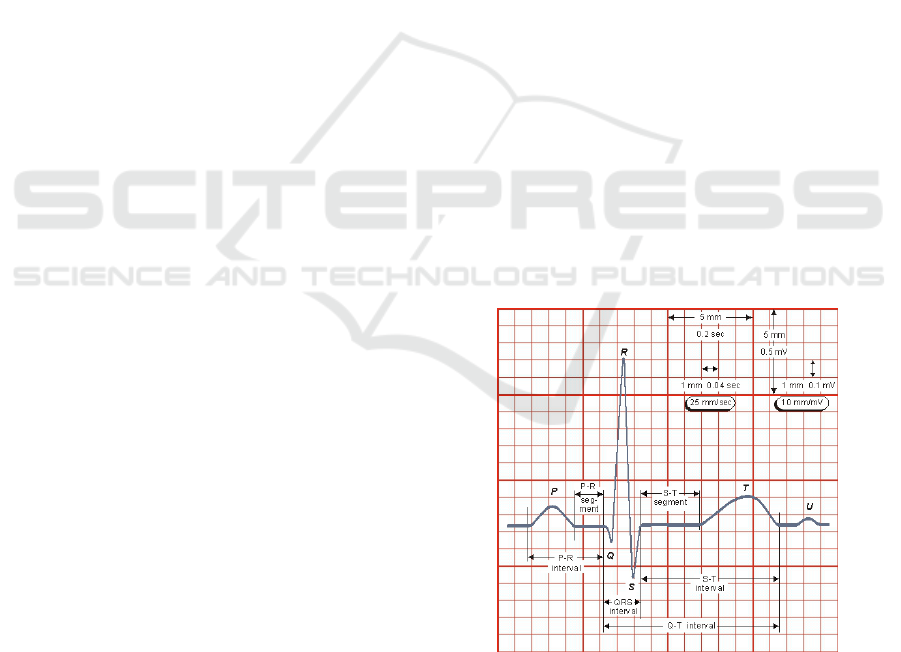
trocardiography, the positions of QRS complexes (see
Fig. 1) or ventricular beats serve as a basis for fur-
ther analysis of electrocardiogram (ECG). It is for ex-
ample the most crucial task in heart rate variability
(HRV) analysis, which analyses RR interval (distance
between two consecutive R waves) changes during
long periods of time in order to detect heart disorders.
The necessity of correct detection arises with each
application of QRS detection algorithms. Many re-
searchers proposed large variety of methods for solv-
ing this task (Friesen et al., 1990; Pal and Mitra, 2012;
Pan and Tompkins, 1985; Christov, 2004). The most
commonly used in real world applications is Pan-
Tompkins QRS detection algorithm (Pan and Tomp-
kins, 1985).
Pan-Tompkins algorithm is based on patient-
specific detection threshold. Algorithms work on sin-
gle lead ECG, which is modified by set of preprocess-
ing digital filters in order to enhance positions of QRS
complexes. Next the patient specific detection thresh-
old is computed. The value of threshold is determined
by difference of the noise amplitude median and R
wave amplitude median. Pan-Tomkins algorithm has
higher accuracy for various beat morphologies and it
outperforms methods developed earlier.
Figure 1: ECG wave form description. In the middle the
QRS complex is presented. Taken from (Malmivuo and
Plonsey, 1995) with permission.
2 DATA AND METHODS
2.1 Data
In our experiments we used data freely available on
MIT medical storage Physionet (Goldberger et al.,
2000).
We used MIT-BIH Arrhytmia database (Moody
and Mark, 2001), which contains 48 half-hour two
channel ambulatory ECG recordings digitized at 360
280
Kuzilek J. and Lhotska L..
Beat Detection Enhancing using AdaBoost.
DOI: 10.5220/0004195202800283
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 280-283
ISBN: 978-989-8565-36-5
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

samples per second with 11-bit resolution over 10 mV
range annotated by two or more cardiologist.
2.2 AdaBoost
Adaptive Boosting (AdaBoost) algorithm is a ma-
chine learning meta-algorithm for enhancing perfor-
mance of other algorithms (Chang et al., 2010). Ad-
aBoost creates a strong classifier using linear combi-
nation of weak classifiers. The main purpose of the
algorithm is to reduce error on specific data using set
of weak classifiers. The algorithm is shown in Algo-
rithm 1. The algorithm works with the training dataset
X and its classification Y . AdaBoost exponentially re-
duces the classification error.
AdaBoost algorithm can be successfully applied
on balanced data set, where both classes {−1, +1}
have the same frequency. If the dataset is imbal-
anced modification in AdaBoost algorithm is required
(Stamkopoulos et al., 1998). There are several pos-
sible modifications of AdaBoost algorithm available.
For example: AdaCost, CSB1, CSB2 or RareBoost.
For more details see (Stamkopoulos et al., 1998).
Algorithm 1: AdaBoost algorithm.
Input: (x
1
,y
1
),...,(x
m
,y
m
) where x
i
∈ X,
y
i
∈ {−1, +1}; number of iterations T
1: Initialize sample weights D
1
(i) =
1
m
2: for t = 1, ..., T do
3: Choose the best weak classifier h
t
with the
smallest error:
h
t
= arg min
h
j
∈H
ε
j
;ε
j
=
m
∑
i=1
D
t
(i)[y
i
6= h
i
],
4: Compute weight α
t
of h
t
in final strong classi-
fier:
α
t
=
1
2
log
1 − ε
t
ε
t
.
5: Update and normalize sample weights:
D
t+1
(i) =
D
t
(i)exp(−α
t
y
i
h
t
(x
i
))
Z
t
,
where Z
t
=
∑
m
i=1
D
t
(i)exp(−α
t
y
i
h
t
(x
i
)), α
t
6: end for
Output: Strong classifier H(x) consisting of T weak
classifiers:
H(x) = sign
T
∑
t=1
α
t
h
t
(x)
!
2.3 Weak QRS Detectors
In our study we used several weak QRS detectors for
the demonstration of the algorithm principle. The set
of weak detectors contain:
• QRS detectors based on amplitude threshold
Based on fixed amplitude threshold. Each detec-
tor has different threshold differing by 0.1 mV.
• QRS detectors based on first derivative and
threshold
Based on fixed thresholding of differentiated sig-
nal. Each detector has different threshold differ-
ing by 0.01 mV.
Every QRS detector can be considered as classi-
fier into two classes:
• nonQRS class (-1)
Samples lying outside the QRS complex.
• QRS class (+1)
Samples within QRS complex.
In our case the set of weak QRS detectors is also set of
one dimensional linear classifiers, where the feature is
the sample amplitude or difference between two sam-
ples. The decision boundary is at threshold.
2.4 Algorithm
We ask the question - can we merge the QRS detectors
together in order to enhance the overall QRS detec-
tion? Our algorithm (QRSBoost) is the answer - us-
ing AdaBoost with combination of several basic QRS
detectors gives us stronger QRS detector comparable
with gold standard detector (Pan-Tompkins detector).
There are several difficulties with adapting Ad-
aBoost algorithm for combining QRS detectors. The
most problematic one is how to annotate data for
learning. The best solution is to define whole QRS
complex samples as positive class samples during
learning. This implies that all weak detectors needs
to return positions of every positive sample not only
the position of R-peak, which is considered as starting
point of analysis. This extension during learning pro-
cess enables us to find strongest QRS detector more
accurately and also reduces the imbalanced dataset
problem (most samples in signal are non-QRS). An-
other reduction of imbalanced dataset problem is done
by setting different starting weights for positive and
negative class.
The algorithm is depicted in Algorithm 2. We can
observe that the main modification lies in initializa-
tion step, when data and their weights are prepared for
AdaBoost itself. So the input data are in our case sam-
ples of ECG data (X) and their classification (Y) into
nonQRS and QRS class. To the samples there are as-
signed the weights, which express importance of the
sample during the AdaBoost learning. The QRS class
BeatDetectionEnhancingusingAdaBoost
281

has higher importance than nonQRS class because of
smaller frequency in data. Then the AdaBoost algo-
rithm starts. It makes detection of QRS complexes
for each QRS detector from the set of input weak de-
tectors and chooses the best one (it uses classifica-
tions and sample weights). Then the weight of the
selected classifier is computed and weights of sam-
ples are recomputed (correctly founded samples have
lower weight now and falsely detected samples have
larger weight). After this AdaBoost starts next itera-
tion.
Algorithm 2: QRSBoost algorithm.
Input: (x
1
,y
1
),...,(x
m
,y
m
) where x
i
∈ X,
y
i
∈ {−1, +1}; number of iterations T
1: Recompute annotations to whole QRS complex
2: Initialize sample weights D
1
(i) =
1
m
3: Set weights of positive class (beat detected) n-
times larger, where n is fraction number of QRS
complex samples in whole database
4: for t = 1, ..., T do
5: Choose the best weak QRS detector h
t
with the
smallest error:
h
t
= arg min
h
j
∈H
ε
j
;ε
j
=
m
∑
i=1
D
t
(i)[y
i
6= h
i
],
6: Compute weight α
t
of h
t
in the final strong
QRS detector:
α
t
=
1
2
log
1 − ε
t
ε
t
.
7: Update and normalize sample weights:
D
t+1
(i) =
D
t
(i)exp(−α
t
y
i
h
t
(x
i
))
Z
t
,
where Z
t
=
∑
m
i=1
D
t
(i)exp(−α
t
y
i
h
t
(x
i
)), α
t
8: end for
Output: Strong QRS detector H(x) consisting of T
weak QRS detectors:
H(x) = sign
T
∑
t=1
α
t
h
t
(x)
!
3 EVALUATION
For evaluation we used standard statistical indices
Sensitivity (Se) and Positive predictivity (P
+
), which
are derived from three parameters:
• Correctly detected beats (True positives=T P)
• Falsely detected beats (False positives=FP)
• Undetected beats (False negatives=FN)
Sensitivity is the parameter describing how many
beats are correctly detected. Thus its value is calcu-
lated using this equation:
Se =
T P
T P + FN
. (1)
Positive predictivity characterizes the algorithm in
sense of the false detection of beats. Its value is es-
timated as follows:
P
+
=
T P
T P + FP
. (2)
All statistical indices ranges from 0 % (worst) to 100
% (best). The values over 95 % are considered as
good results. We also measured the average time
consumed by the algorithms for detection of QRS
complexes in the database. The average time is de-
fined as:
AvgTime =
∑
L
i=1
t
i
L
, (3)
where L is number of recordings (for MIT/BIH Ar-
rhythmia database is L=48) and t
i
is time for complet-
ing of QRS detection on i-th record.
4 RESULTS
Table 1 shows summarized results for Pan-Tompkins
beat detection algorithm and our QRSBoost algorithm
(combination of 4 weak QRS detectors, T=4) on the
MIT/BIH Arrhythmia Database. We can observe that
results are quite similar - both algorithms achieves in
Se and P
+
measures around 95%, which can be con-
sidered as a good result.
On the other hand our algorithm is much more
easier for implementation - it combines 4 weak
threshold QRS detectors using their linear combina-
tion. These detectors have very low time complexity
and their linear combination too. In comparison Pan-
Tompkins algorithm uses several filtering steps for
signal preprocessing and adaptive threshold, which
needs to be recomputed during the algorithm run.
This makes algorithm much slower than our algo-
rithm.
Table 1: Results.
Algorithm
Pan-Tompkins AdaBoost
Se [%] P+ [%] Time [ms] Se [%] P+ [%] Time [ms]
94.16 98.77 506 96.11 94.04 422
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
282

5 CONCLUSIONS
We developed an algorithm for enhancing QRS detec-
tion using set of weak QRS detectors. This algorithm
is based on AdaBoost machine learning algorithm. It
enables us to combine set of QRS detectors by their
linear combination. The results of the combined QRS
detector are much more accurate than each detector
from the input set. The time complexity of our al-
gorithm depends mainly on time complexity of weak
QRS detectors used in combination.
The results are preliminary ones and we plan to
measure exact times of QRSBoost algorithm during
the detection in order to get better comparison with
golden standard Pan-Tompkins algorithm. We also
plan to try different weak QRS detectors to enhance
detection rate. Finally we intend to implement the
resulting algorithm in real-time, which is feasible be-
cause the linear combination is not difficult to imple-
ment.
ACKNOWLEDGEMENTS
Research described in the paper has been supported
by the CTU Grant SGS10/279/OHK3/3T/13, research
program No. MSM 6840770012 ”Transdisciplinary
Research in Biomedical Engineering II” of the CTU
in Prague.
REFERENCES
Chang, P.-C., Hsieh, J.-C., Lin, J.-J., and Yeh, F.-M. (2010).
Atrial fibrillation analysis based on blind source sepa-
ration in 12-lead ecg data. In Zhang, D. and Sonka,
M., editors, Medical Biometrics, volume 6165 of
Lecture Notes in Computer Science, pages 286–295.
Springer Berlin Heidelberg.
Christov, I. (2004). Real time electrocardiogram qrs de-
tection using combined adaptive threshold. BioMedi-
cal Engineering OnLine, 3(1):28. M3: 10.1186/1475-
925X-3-28.
Friesen, G., Jannett, T., Jadallah, M., Yates, S., Quint, S.,
and Nagle, H. (1990). A comparison of the noise sen-
sitivity of nine qrs detection algorithms. Biomedical
Engineering, IEEE Transactions on, 37(1):85 –98.
Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff,
J. M., Ivanov, P. C., Mark, R. G., Mietus, J. E., Moody,
G. B., Peng, C. K., and Stanley, H. E. (2000). Phys-
ioBank, PhysioToolkit, and PhysioNet : Components
of a New Research Resource for Complex Physiologic
Signals. Circulation, 101(23):e215–220.
Malmivuo, J. and Plonsey, R. (1995). Bioelectromagnetism
: Principles and Applications of Bioelectric and Bio-
magnetic Fields. Oxford University Press, USA, 1 edi-
tion.
Moody, G. and Mark, R. (2001). The impact of the mit-
bih arrhythmia database. Engineering in Medicine and
Biology Magazine, IEEE, 20(3):45 –50.
Pal, S. and Mitra, M. (2012). Empirical mode decomposi-
tion based ecg enhancement and qrs detection. Com-
puters in biology and medicine, 42(1):83–92.
Pan, J. and Tompkins, W. J. (1985). A real-time qrs detec-
tion algorithm. Biomedical Engineering, IEEE Trans-
actions on, BME-32(3):230–236.
Stamkopoulos, T., Diamantaras, K., Maglaveras, N., and
Strintzis, M. (1998). Ecg analysis using nonlinear pca
neural networks for ischemia detection. Signal Pro-
cessing, IEEE Transactions on, 46(11):3058 –3067.
BeatDetectionEnhancingusingAdaBoost
283
