6D Visual Odometry with Dense Probabilistic Egomotion Estimation

Hugo Silva

, Alexandre Bernardino

and Eduardo Silva

INESC TEC Robotics Unit, ISEP, Rua Dr. Antonio Bernardino de Almeida 431, Porto, Portugal

Institute of Systems and Robotics, IST, Avenida Rovisco Pais 1, Lisboa, Portugal

Keywords:

Visual Navigation, Stereo Vision, Visual Odometry, Egomotion.

Abstract:

We present a novel approach to 6D visual odometry for vehicles with calibrated stereo cameras. A dense

probabilistic egomotion (5D) method is combined with robust stereo feature based approaches and Extended

Kalman Filtering (EKF) techniques to provide high quality estimates of vehicle’s angular and linear velocities.

Experimental results show that the proposed method compares favorably with state-the-art approaches, mainly

in the estimation of the angular velocities, where signiﬁcant improvements are achieved.

1 INTRODUCTION

Visual Odometry is the term generically used to de-

note the process of estimating linear and angular ve-

locities of a vehicle equipped with vision cameras

(Scaramuzza and Fraundorfer, 2011). These systems

are becoming ubiquitous in mobile robotics applica-

tions due to the availability of low-cost high qual-

ity cameras and their ability to complement the mea-

surements provided by Inertial Measurement Units

(IMU). Because vision sensors ground their percep-

tion on static features of the environment, they are in

principle less prone to the estimation bias rather com-

mon on IMU sensors. In this work we focus on the

development of Visual Odometry Systems for mobile

robots equipped with a calibrated stereo camera setup.

Visual Odometry Systems are an important com-

ponent on mobile robot’s navigation systems. The

short term velocity estimates provided Visual Odome-

try has been shown to improve the localization results

of Simultaneous Localization and Mapping (SLAM)

methods. For instance in (Alcantarilla et al., 2010),

Visual Odometry measurements are used as priors for

the prediction step of a robust EKF-SLAM algorithm.

Visual Odometry systems have been continuously

developed over the past 30 years. These systems suf-

fered a major outbreak due to the outstanding work of

(Maimone and Matthies, 2005) on NASA Mars Rover

Program. Nister ((Nist

er, 2004)) developed a Visual

Odometry system, based on a 5-point algorithm, that

became the standard algorithm for comparison of Vi-

sual Odometry techniques. This algorithm can be

used either in stereo or monocular vision approaches

and consists on the use of several visual processing

techniques, namely: feature detection and matching,

tracking, stereo triangulation and RANSAC (Fischler

and Bolles, 1981) for pose estimation with iterative

reﬁnement.

In (Moreno et al., 2007) it is proposed a visual

odometry estimation method using stereo cameras. A

closed form solution is derived for the incremental

movement of the cameras and combines distinctive

features SIFT (Lowe, 2004) with sparse optical ﬂow.

There are already some approaches to stereo vi-

sual odometry estimation using dense methods like

the one developed by (Comport et al., 2007), that uses

a quadrifocal warping function to track features us-

ing dense correspondences to correctly estimate 3D

visual odometry.

In (Domke and Aloimonos, 2006), a method for

estimating the epipolar geometry describing the mo-

tion of a camera is proposed using dense probabilis-

tic methods. Instead of deterministically choosing

matches between two images, a probability distribu-

tion is computed over all possible correspondences.

By exploiting a larger amount of data, a better perfor-

mance is achieved under noisy measurements. How-

ever, that method is more computationally expensive

and does not recover translational scale factor.

In our work, we propose the use of a dense prob-

abilistic method such as in (Domke and Aloimonos,

2006) but with two important additions: (i) a sparse

feature based method is used to estimate the trans-

lational scale factor and (ii) a fast correspondence

method using a recursive ZNCC implementation is

provided for computational efﬁciency.

361

Silva H., Bernardino A. and Silva E..

6D Visual Odometry with Dense Probabilistic Egomotion Estimation.

DOI: 10.5220/0004196103610365

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 361-365

ISBN: 978-989-8565-48-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Our method, denoted 6DP combines sparse fea-

ture detection and tracking for stereo-based depth

estimation, using highly distinctive SIFT features

(Lowe, 2004) and a variant of the dense probabilistic

ego-motion method developed by (Domke and Aloi-

monos, 2006) to estimate camera motion up to a trans-

lational scale factor. Upon obtaining two registered

point sets in consecutive time frames, an Absolute

Orientation method, deﬁned as an orthogonal Pro-

crustes problem (AO) is used to recover yet unde-

termined motion scale. The velocities obtained by

the proposed method are then ﬁltered with a EKF ap-

proach to reduce sensor noise and provide frame-to-

frame ﬁltered linear and angular velocity estimates.

Our method was compared with the methods in

LIBVISO Visual Odometry Library (Kitt et al., 2010),

using standard dataset from this library. Ground truth

is also provided, through the fusion of IMU and

GPS measurements. Results show that our method

presents signiﬁcant improvements in the estimation of

angular velocities and a similar performance for linear

velocities. The beneﬁts of using dense probabilistic

approaches are thus validated in a real world scenario

with practical signiﬁcance.

2 6D VISUAL ODOMETRY USING

DENSE AND SPARSE

EGO-MOTION ESTIMATION

Our solution is based on the probabilistic method of

egomotion estimation using the epipolar constraint

developed by (Domke and Aloimonos, 2006). How-

ever, the method from (Domke and Aloimonos, 2006)

is unable to estimate motion scale, so a stereo vi-

sion sparse feature based approach that uses detected

SIFT features correspondence between I

T k

and I

T k+1

is used to obtain translation motion scale.

An architecture of our method is displayed in ﬁg-

ure 1. In summary, it is composed by the following

main steps:

1. First, SIFT feature points are detected in the cur-

rent pair of stereo frames (I

T k

, I

T k

), using a known

feature detector. These image feature points are

then correlated between left and right image to ob-

tain 3D point depth information.

2. Second, we use a dense image pixel correlation

method, that due to its probabilistic nature, does

not commit the match correlation of image point

(x, y) in I

T k

to other image point P

(x, y) in

T k+1

. Instead, it copes with several hypothe-

sis of matching for image point P

(x, y) in I

T k+1

thus making the estimation of the essential matrix

Figure 1: 6D Visual Odometry System Architecture.

more robust to image feature matching errors

and hence providing a more accurate camera mo-

tion estimation [R,t] between I

T k

and I

T k+1

. The

dense likelihood correspondence maps are com-

puted based on ZNCC(Huang et al., 2011) corre-

lation.

3. Third, due to the need to determine the motion

scale between I

T k

and I

T k+1

, a Procrustes abso-

lute orientation method(AO) is utilized. The AO

method uses 3D image feature points obtained

by triangulation from stereo image pairs (I

T k

, I

T k

)

and (I

T k+1

, I

T k+1

) combined with robust tech-

niques like RANSAC(Fischler and Bolles, 1981),

thus obtaining only good candidates (inliers) for

Procrustes based motion scale determination.

4. Finally, vehicle linear and angular velocity (V, Ω)

between I

T k

and I

T k+1

is determined.

All, of this steps are then encapsulated within an

Extended Kalman ﬁlter yielding a more robust camera

motion estimation.

2.1 Probabilistic Correspondence

The key to the proposed method relies in the con-

sideration of probabilistic rather than deterministic

matches. Usual methods for motion estimation con-

sider a match function M that associates coordinates

of points m = (x, y) in image 1 to points m

= (x

, y

)

in image 2 :

M(m) = m

(1)

Instead, the probabilistic correspondence method de-

ﬁnes a probability distribution over the points in im-

age 2 for all points in image 1:

) = P(m

|m) (2)

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

362

Figure 2: Image feature Point correspondence for ZNCC

matching.

Thus, all points m

in image 2 are candidates for

matching with point m in image 1 with a priori like-

lihoods proportional to P

). One can consider P

as images (one per each pixel in image 1) whose value

in m

is proportional to the likelihood of m

matching

with m. For the sake of computational cost, likeli-

hoods are not computed for the whole range in image

2 but just to windows around m (or suitable predic-

tions given prior information), see ﬁgure 2.

In (Domke and Aloimonos, 2006) this value was

computed via the normalized product, over a ﬁlter

bank of Gabor ﬁlters with different orientation and

scales, of the exponential of the negative differences

between the angle of the Gabor ﬁlter responses in m

and m

The motivation for using a Gabor ﬁlter bank was

the robustness of their responses to changes in the

brightness and contrast of the image. However, the

computations demand a signiﬁcant computational ef-

fort, thus we propose to perform the computations

with the well known Zero Mean Normalized Cross

Correlation function(ZNCC).

This function is also known to be robust to bright-

ness and contrast changes and recent efﬁcient recur-

sive schemes developed by Huang et al (Huang et al.,

2011) render it suitable to real-time implementations.

That method is faster to compute and yields the same

quality as the method of Domke.

2.1.1 Probabilistic Egomotion

From two images of the same camera, one can recover

its motion up to the translation scale factor. This can

be represented by the epipolar constraint which, in ho-

mogeneous normalized coordinates can be written as:

)

Es = 0 (3)

where E is the so called Essential Matrix (Hartley and

Zisserman, 2004), a 3X3 matrix with rank 2 and 5

degrees-of-freedom. Intuitively, this matrix expresses

the directions in image 2 that should be searched for

matches of points in image 1. It can be factored by:

E = R [t]

(4)

where R and t are, respectively, the rotation and trans-

lation of the camera between the two frames.

To obtain the Essential matrix from the probabilis-

tic correspondences, (Domke and Aloimonos, 2006)

proposes the computation of a probability distribution

over the (5-dimensional) space of essential matrices.

Each dimension of the space is discretized in 10 bins,

thus leading to 100000 hypotheses E

. For each point

s the likelihood of these hypotheses are evaluated by:

P(E

|s) ∝

max

: (s

)

s = 0 P

) (5)

Intuitively, for a single point s in image 1, the like-

lihood of a motion hypothesis is proportional to the

best match obtained along the epipolar line generated

by the essential matrix. Assuming independence, the

overall likelihood of a motion hypothesis is propor-

tional to the product of the likelihoods for all points:

P(E

) ∝ Π

P(E

|s) (6)

After a dense correspondence probability distri-

bution has been computed for all points, the method

(Domke and Aloimonos, 2006) computes a probabil-

ity distribution over motion hypotheses represented

by the epipolar constraint. Finally, given the top

ranked motion hypotheses, a Nelder-Mead simplex

method (Lagarias et al., 1998) is used to reﬁne the

motion estimate.

However, since the current method does not allow

motion scale recovery, translation T

component does

not contain image scale information. This type of in-

formation, is calculated by an alternative absolute ori-

entation method like the Procrustes method.

2.2 Procrustes Analysis and Scale

Factor Recovery

The Procrustes method allows to recover rigid body

motion between frames, through the use of 3D point

matches. We assume a set of 3D features (computed

by triangulation of SIFT features) in instant t

T k

be de-

scribed by

{

}

T k

, move to a new position and orien-

tation in t

T k+1

, described by

{

}

T k+1

. This transfor-

mation can be represented as:

= RX

+ T (7)

where Y

points, are 3D feature points in I

T k+1

These points were detected using SIFT descriptors

between I

T k

and I

T k+1

, that were triangulated to their

stereo corresponding matches in I

T k+1

6DVisualOdometrywithDenseProbabilisticEgomotionEstimation

363

These two sets of points are the ones that are used

by Procrustes method to estimate motion scale.

In order to estimate motion [R,T], a cost function

that measures the sum of squared distances between

corresponding points is used.

∑



− (RX

+ T )



(8)

Performing minimization of equation (8), gives

estimates of [R, T ]. Although conceptually simple,

some aspects regarding the practical implementation

of the Procrustes method must be taken into con-

sideration. Namely, since this method is very sen-

sible to data noise, obtained results tend to vary in

the presence of outliers. To overcome this difﬁ-

culty, RANSAC (Fischler and Bolles, 1981) is used

to discard possible outliers within the set of matching

points.

For a correct motion scale estimation, it is nec-

essary to have a proper spatial feature distribution

through out the image. For instance, if the Procrustes

method uses all obtained image feature points without

having their image spatial distribution into consider-

ation, the obtained motion estimation [R,T] between

two consecutive images could turn out biased.

Given these facts, to avoid having biased samples

in the RANSAC phase of the algorithm, a bucket-

ing technique (Zhang et al., 1995) is implemented to

assure a unbiased image feature distribution sample.

After, completing all this steps, only valid points are

used in Procrustes method application. We then use

an Extended Kalman ﬁlter to help robust camera lin-

ear and angular velocity estimates, and also to esti-

mate vehicle pose between different time frames.

3 RESULTS

To illustrate the performance of our 6D Visual Odom-

etry method, we compared our system performance

against LIBVISO (Kitt et al., 2010), which is a stan-

dard library for computing 6 DOF motion. We also

compared our performance against Inertial Measure-

ment Unit (RTK-GPS information) using part of one

of Kitt et al(Kitt et al., 2010) Karlsruhe dataset se-

quences.

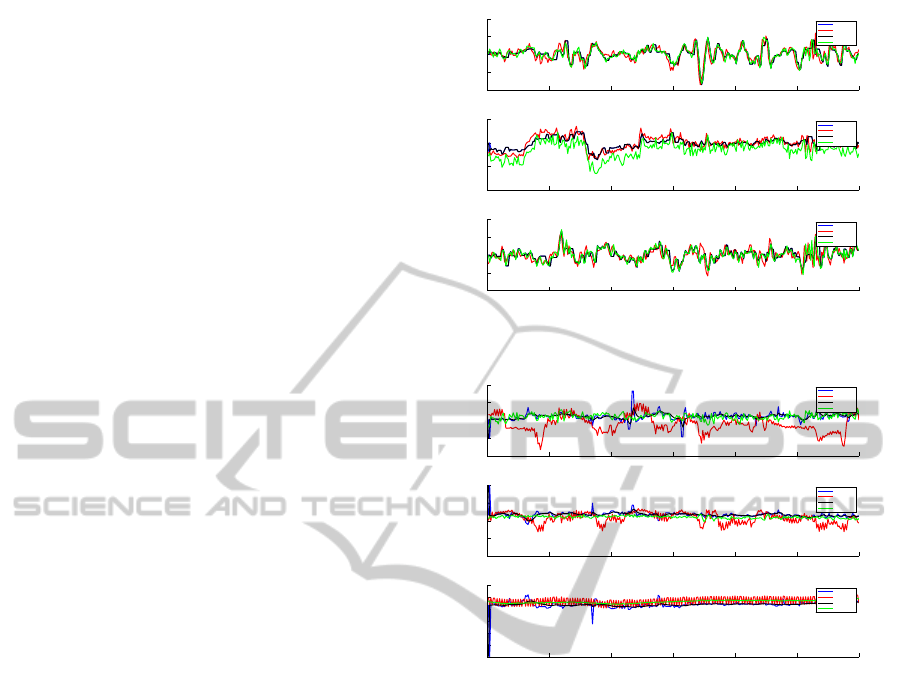
In ﬁgure 3 one can observe angular velocity esti-

mation from both IMU and LIBVISO, together with

6dp-RAW and EKF ﬁltered measurements. All vision

approaches obtained results are consistent with the In-

ertial Measurement Unit, but the 6dp-EKF displays a

better performance in what respects the angular veloc-

ities. These results are stated in table (1), where root

0 50 100 150 200 250 300

−2

−1

Angular Velocity Wx

Frame Index

Wx degree/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

0 50 100 150 200 250 300

−1

−0.5

0.5

Angular Velocity Wy

Frame Index

Wy degree/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

0 50 100 150 200 250 300

−2

−1

Angular Velocity Wz

Frame Index

Wz degree/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

Figure 3: Angular Velocity Estimation Results.

0 50 100 150 200 250 300

−0.1

0.1

0.2

0.3

Linear Velocity Vx

Frame Index

Vx m/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

0 50 100 150 200 250 300

−0.8

−0.6

−0.4

−0.2

Linear Velocity Vy

Frame Index

Vy m/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

0 50 100 150 200 250 300

Linear Velocity Vz

Frame Index

Vz m/s

6dp−RAW

IMU

6dp−EKF

LIBVISO

Figure 4: Linear Velocity Estimation Results.

mean square error between IMU and LIBVISO, 6DP-

EKF estimation are displayed. Both methods display

considerable low standard deviation results, but with

6DP-EKF displaying 50% less than LIBVISO for the

angular velocities estimation.

Although not as good as the angular velocities, the

6dp-EKF method also displays a stable performance

in obtaining linear velocity estimates using the sparse

feature approach based on SIFT features combined

with Procrustes Absolute Orientation method, as dis-

played in ﬁgure 4.

4 CONCLUSIONS AND FUTURE

WORK

In this paper, we developed a novel method for con-

ducting 6D visual odometry based on the use of dense

Probabilistic Egomotion estimation approach. We

also complemented this method with a sparse feature

approach for estimating image depth. We tested the

proposed algorithm against a state-of-the-art 6D vi-

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

364

Table 1: Standard Mean Squared Error between IMU and Visual Odometry (LIBVISO and 6dp-EKF).

Ω

LIBVISO 0.0674 0.7353 0.3186 0.0127 0.0059 0.0117

6DP-EKF 0.0884 0.0748 0.7789 0.0049 0.0021 0.0056

sual Odometry Library such as LIBVISO.

The presented results demonstrate that 6DP per-

forms accurately when compared to other techniques

for 6-DOF visual Odometry estimation, yielding ro-

bust motion estimation results, mainly in the angular

velocities estimation results.

In future work, we want to extend our dense prob-

abilistic method to developed a standalone approach

for ego-motion estimation that can cope with motion

scale estimation, by using other type of multiple view

geometry parametrization.

ACKNOWLEDGEMENTS

This work is ﬁnanced by the ERDF

a European Re-

gional Development Fund through the COMPETE

Programme (operational programme for competitive-

ness) and by National Funds through the FCT Funda-

cao para a Ciencia e a Tecnologia (Portuguese Foun-

dation for Science and Technology) within project

FCOMP - 01-0124-FEDER-022701 and under grant

SFRH / BD / 47468 / 2008 .

REFERENCES

Alcantarilla, P., Bergasa, L., and Dellaert, F. (2010). Vi-

sual odometry priors for robust EKF-SLAM. In IEEE

International Conference on Robotics and Automa-

tion,ICRA 2010, pages 3501–3506. IEEE.

Civera, J., Grasa, O., Davison, A., and Montiel, J. (2010). 1-

Point RANSAC for EKF ﬁltering. Application to real-

time structure from motion and visual odometry. Jour-

nal of Field Robotics, 27(5):609–631.

Comport, A., Malis, E., and Rives, P. (2007). Accurate

Quadri-focal Tracking for Robust 3D Visual Odom-

etry. In IEEE International Conference on Robotics

and Automation, ICRA’07, Rome, Italy.

Domke, J. and Aloimonos, Y. (2006). A Probabilistic

Notion of Correspondence and the Epipolar Con-

straint. In Third International Symposium on 3D

Data Processing, Visualization, and Transmission

(3DPVT’06), pages 41–48. IEEE.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: A paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6):381–395.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Huang, J., Zhu, T., Pan, X., Qin, L., Peng, X., Xiong, C.,

and Fang, J. (2011). A high-efﬁciency digital image

correlation method based on a fast recursive scheme.

Measurement Science and Technology, 21(3).

Kitt, B., Geiger, A., and Lategahn, H. (2010). Visual odom-

etry based on stereo image sequences with ransac-

based outlier rejection scheme. In IEEE Intelligent Ve-

hicles Symposium (IV), 2010, pages 486–492. IEEE.

Lagarias, J. C., Reeds, J. A., Wright, M. H., and Wright,

P. E. (1998). Convergence properties of the nelder–

mead simplex method in low dimensions. SIAM J. on

Optimization, 9(1):112–147.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Maimone, M. and Matthies, L. (2005). Visual Odometry on

the Mars Exploration Rovers. In IEEE International

Conference on Systems, Man and Cybernetics, pages

903–910. Ieee.

Moreno, F., Blanco, J., and Gonz

alez, J. (2007). An efﬁcient

closed-form solution to probabilistic 6D visual odom-

etry for a stereo camera. In Proceedings of the 9th

international conference on Advanced concepts for

intelligent vision systems, pages 932–942. Springer-

Verlag.

Ni, K., Dellaert, F., and Kaess, M. (2009). Flow separation

for fast and robust stereo odometry. In IEEE Interna-

tional Conference on Robotics and Automation ICRA

2009, volume 1, pages 3539–3544.

Nist

er, D. (2004). An efﬁcient solution to the ﬁve-point rel-

ative pose problem. IEEE Trans. Pattern Anal. Mach.

Intell., 26:756–777.

Nist

er, D., Naroditsky, O., and Bergen, J. (2006). Visual

odometry for ground vehicle applications. Journal of

Field Robotics, 23(1):3–20.

Scaramuzza, D. and Fraundorfer, F. (2011). Visual odom-

etry [tutorial]. Robotics Automation Magazine, IEEE,

18(4):80 –92.

Scaramuzza, D., Fraundorfer, F., and Siegwart, R. (2009).

Real-time monocular visual odometry for on-road ve-

hicles with 1-point ransac. In Robotics and Automa-

tion, 2009. ICRA ’09. IEEE International Conference

on, pages 4293 –4299.

Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.

(1995). A robust technique for matching two uncal-

ibrated images through the recovery of the unknown

epipolar geometry. Artiﬁcial Intelligence Special Vol-

ume on Computer Vision, 78(2):87 – 119.

6DVisualOdometrywithDenseProbabilisticEgomotionEstimation

365