Face Recognition using Modiﬁed Generalized Hough Transform

and Gradient Distance Descriptor

Marian Moise, Xue Dong Yang and Richard Dosselmann

Department of Computer Science, University of Regina, 3737 Wascana Parkway, Regina, Saskatchewan, Canada

Keywords:

Face Recognition, Generalized Hough Transform, Image Descriptors.

Abstract:

This research uses a modiﬁed version of the generalized Hough transform based on a new image descriptor,

known as the gradient distance descriptor, to tackle the problem of face recognition. Thus, in addition to

the position of the edges in a sketch of a face, this approach also takes into consideration the value of the

corresponding descriptors. Individual descriptors are compared against one another using the matrix cosine

similarity measure. This enables the technique to identify the region of a query face image that best matches a

target face image in a database. The proposed technique does not require any training data and can be extended

to general object recognition.

1 INTRODUCTION

One of the most important problems in computer vi-

sion is that of face recognition (Li and Jain, 2011).

This paper addresses the problem using a modiﬁed

form of the generalized Hough transform (Ballard,

1981) (GHT), along with a new image descriptor

(Goshtasby, 2012), known as the gradient distance

descriptor (GDD). This method therefore combines

the ability of the GHT to ﬁnd shapes with the power

of descriptors to describe features that may be ob-

scured by deformations or varying illumination con-

ditions. And, because any descriptor may ultimately

be used, the performance of this approach will con-

tinue to improve as descriptors become more discrim-

inative. This combination of techniques further en-

ables the method to capture both the global and local

structure of a face. What’s more, unlike many other

approaches, this method does not require any training

data. Additionally, it can be further extended to gen-

eral object recognition. As part of a preliminary study,

the new approach is tested on the Yale face database

(Yale, 1997). This particular database allows one to

avoid, for the moment, problems of face alignment,

cropping and background removal. The foremost ap-

plication of this work is that of video surveillance in

situations in which there is a given database of target

individuals. Note that the ideas outlined in this paper

were ﬁrst presented in (Moise, 2012).

The GHT has been previously employed in other

tasks, such as the recognition of handwritten Chinese

characters (Li and Dai, 1995), template-based image

matching (Li and Zhang, 2005) or sketch-based im-

age retrieval (Anelli et al., 2007). In (Schubert, 2000),

real-time face detection and tracking is performed us-

ing the GHT. As part of a more elaborate approach

(Barinova et al., 2012), Hough forests (Gall and Lem-

pitsky, 2009) are trained on image patches to detect

multiple faces, such as pedestrians in crowded places.

Among the earliest methods in the ﬁeld of face recog-

nition are those of Eigenfaces (Turk and Pentland,

1991) and Fisherfaces (Belhumeur et al., 1997). Of

these two, Fisherfaces is generally perceived as being

superior given that it reduces intra-class differences

between faces of the same individual. As well, it ap-

pears to be the better of the two at handling variations

in lighting, changes in facial expressions and the pres-

ence of glasses.

Several additional descriptors are considered in

this work. The ﬁrst of these is the locally adaptive re-

gression kernel (Seo and Milanfar, 2011) (LARK) de-

scriptor. It is derived from other descriptors via prin-

cipal component analysis (Duda et al., 2001) (PCA).

In another approach (Seo and Milanfar, 2009), a query

image is divided into a set of overlapping patches

that are compared with those of a target image us-

ing the matrix cosine similarity (Seo and Milanfar,

2010) (MCS) measure. Two additional descriptors

examined in this paper are the self similarities local

descriptor (Shechtman and Irani, 2007) (SSLD) and

one based on the discrete cosine transform (Gonzalez

and Woods, 2002) (DCT).

Moise M., Yang X. and Dosselman R. (2013).

Face Recognition using Modiﬁed Generalized Hough Transform and Gradient Distance Descriptor.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 5-10

DOI: 10.5220/0004198000050010

 SciTePress

2 METHOD

First proposed in (Ballard, 1981), the GHT is a

method of ﬁnding an arbitrary, non-analytic shape

in an image using predeﬁned boundary information.

Together, these boundaries, or edges (Gonzalez and

Woods, 2002), make up a sketch of a shape. The

GHT creates a template of a sketch of a shape us-

ing this edge information. This template, also called

an R-table (Ballard, 1981), stores the locations of the

edge points relative to a reference point, which can be

thought of as the origin of the system of coordinates.

During the recognition process, each edge point in a

query sketch votes for the location of this reference

point. The resulting maximum accumulated value

represents the assumed reference point of the shape.

This method works even when a sketch becomes dis-

continuous due to noise, minor deformations or par-

tial occlusions (Ballard, 1981).

2.1 Modiﬁed GHT

This section describes the modiﬁed GHT, the name

given to the new approach deﬁned in this paper. The

modiﬁed GHT, like the conventional GHT, compares

a sketch of the face in a query image against sketches

of target faces in a database. All sketches are gener-

ated using a Canny (Canny, 1986) edge detector. An

individual edge point in a sketch is denoted x, while

the complete set of all of the edge points in a sketch

is denoted E. The direction (Gonzalez and Woods,

2002) of a given edge x is denoted φ. The vector be-

tween an edge x and the reference point y is denoted

~r. Note that the reference point y = (x

, y

) of a query

sketch is taken to be the center of mass of all of the

edges in that sketch. Lastly, the descriptor of a given

edge x is denoted D. Note that D may be any image

descriptor, including the GDD of Section 2.2. Just

as in (Ballard, 1981), individual edges x are clustered

into an R-table. The R-table employed in the modiﬁed

GHT is similar to that of the traditional GHT, with the

exception that it includes the individual descriptors D

computed for each of the edges x in a sketch. This

modiﬁed table is shown in Table 1. The R-table is or-

ganized into a number of rows or bins. An individual

bin i contains all edges x with a gradient angle that is

equal, when rounded, to i∆φ, for some step size ∆φ.

Just as with the conventional GHT, when a query

sketch is to be checked against a target sketch, the

modiﬁed GHT compares the descriptors of the in-

dividual edges in the query sketch against those in

the appropriate bin in the R-table of the target im-

age. This comparison of the descriptors is carried

out using the robust matrix cosine similarity measure.

Table 1: Modiﬁed R-table.

i φ

0 0 ~r | φ(x) = 0 D | φ(x) = 0

1 ∆φ ~r | φ(x) = ∆φ D | φ(x) = ∆φ

2 2∆φ ~r | φ(x) = 2∆φ D | φ(x) = 2∆φ

Note that the MCS measure was chosen over the com-

peting correlation (Gonzalez and Woods, 2002) mea-

sure for reasons of accuracy (Schneider and Borlund,

2007). If there is a match between the two descriptors,

then the two are said to represent the same point in a

shape. Accordingly, the matching entry in the Hough

accumulator (Ballard, 1981) array, as usual, is incre-

mented. And, just as always, the entry that receives

the most votes is taken to be the reference point of

the target sketch. In the end, the target image that re-

ceives the highest overall vote count is selected as the

best match to the face in the query image. Pseudocode

of the complete modiﬁed GHT algorithm is presented

in Algorithm 1 of Section 2.2, immediately after the

discussion of the new GDD measure.

Two separate accumulator arrays are visualized in

Figure 1. In both instances, brighter colors corre-

spond to higher vote totals, while darker shades rep-

resent smaller totals. The array shown in Figure 1(a)

was obtained by comparing two images of the same

individual, one in which the person is wearing glasses

and one in which the person is not. One will notice

that there are only a few “signiﬁcant” values in this

array, speciﬁcally those in the range of 3 × 10

and

6 × 10

, with the largest value representing the best

overall position of the reference point. On the other

hand, the various totals in the array of Figure 1(b),

which relates to the comparison of two different in-

dividuals, are noticeably lower, with most lying be-

tween 1.5 × 10

and 3 × 10

. The sizeable gap be-

tween the largest values in the two arrays of Figures

1(a) and 1(b) enables the new algorithm to discrimi-

nate between individuals.

2.2 Gradient Distance Descriptor

Image descriptors characterize an image using at-

tributes such as shape, orientation, edges, luminosity,

color and texture. They can also be used to remove

unwanted parts of an image, including backgrounds,

blurred regions and outlying pixels. Moreover, many

descriptors are invariant to scaling, rotation, shear-

ing, translation, lighting variations and small defor-

mations. Although image descriptors require addi-

tional memory and increase the overall computational

complexity of a problem, they are preferable to raw

pixel intensities as they better represent the features

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

(a)

(b)

Figure 1: Accumulator arrays (originals in color); (a) same

person with and without glasses; (b) two different persons.

of an image than do single pixels.

The new GDD is based on the LARK descriptor.

It was ultimately chosen over the three other compet-

ing measures due to its slightly better performance.

It is the weighted average of the horizontal and verti-

cal image gradients G

and G

(Gonzalez and Woods,

2002), denoted

and

, respectively, of an edge

x, over the pixels in a patch surrounding that edge x.

Formally, for a p × p patch centered on an edge x, the

GDD is given as

GDD(x) =







1,1

1,2

··· d

1,p

2,1

2,2

··· d

2,p

p,1

p,2

··· d

p,p







, (1)

where

m,n

= exp



−



· dx

m,n

· dy

m,n





. (2)

To give more weight to those pixels that are closest to

the center of the descriptor, the average gradients

and

of each entry d

m,n

are scaled by the horizontal

and vertical distances, dx

m,n

and dy

m,n

, respectively,

of a pixel q

m,n

∈ GDD(x) from the center of the de-

scriptor, where

m,n

= n −

p + 1

(3)

and

m,n

= m −

p + 1

. (4)

Lastly, the weighted averages

and

are calcu-

lated using the MatLab

 circular averaging ﬁlter,

denoted here as C

p×p

. Formally,

∑

i=1

∑

j=1

i, j

· G

), (5)

and

∑

i=1

∑

j=1

i, j

· G

), (6)

for weights a

i, j

∈ C

p×p

During the face recognition process, the descrip-

tor D of each edge point x, with a direction of φ, in

a query face sketch is compared, using the matrix co-

sine similarity measure, with those of the edges in the

bin corresponding to this angle φ in the R-table of the

target face sketch. The overall degree of similarity

between two descriptors, as determined via the MCS

measure, is given by δ. Two descriptors are said to

match if δ < ε, for a threshold ε. If a given descriptor

cannot be matched to any of those in a target sketch,

then that descriptor is discarded, and, as a result, the

associated edge point does not take part in the ensuing

voting process. This is captured in the pseudocode of

the complete modiﬁed GHT algorithm, given in Al-

gorithm 1. Note that other descriptors may be substi-

tuted for the GDD in Algorithm 1. As well, C

is an

added constant.

3 RESULTS AND DISCUSSION

The modiﬁed GHT is ﬁrst compared with the popular

Eigenfaces and Fisherfaces approaches. All tests are

performed on the Yale face database. This database

is comprised of 15 subjects, including both males and

females, in 11 different environments, giving a total

of 15 · 11 = 165 images. Each of these 165 images is

individually compared against the other 164 images

in the database. A search is deemed to be successful

if the current image is matched to one of the other ten

images corresponding to the individual in the current

image. In each of the experiments, ε is taken to be

0.05 and C

is set to 10

The plot of Figure 2 shows the overall recognition

rate obtained using Eigenfaces and Fisherfaces.

FaceRecognitionusingModifiedGeneralizedHoughTransformandGradientDistanceDescriptor

A ← 0 {initialize accumulator array A to 0}

R ←

0 {initialize R-table R to empty}

for all x ∈ E do

φ ← direction of x

~r ← x −y {get vector between x and y}

D ← GDD(x)

R ← R ∪ {~r, D}

for all x

∗

∈ R | φ(x) = φ(x

∗

) do

∗

← GDD(x

∗

)

δ ← MCS (D, D

∗

)

if δ < ε then

∗

← x −~r {y

∗

is estimate of y}

A(y

∗

) ← A (y

∗

) + round(C

(ε − δ)) + 1

end if

end for

y ← get max accumulator array vote count(A)

return

y {

y is best estimate of y}

Algorithm 1: Modiﬁed GHT.

0.50

0.55

0.60

0.65

0.70

0.75

5 10152025303540

NUMBER OF EIGENVECTORS

RECOGNITION RATE

Eigenfaces Fisherfaces

Figure 2: Performance comparisons of Eigenfaces and Fish-

erfaces (original in color).

Training for these two techniques was carried out

using 60 of the 165 images in the database, with

the remaining 105 used for testing. The Fisherfaces

procedure, as expected, outperforms the competing

Eigenfaces method. The modiﬁed GHT, not explic-

itly shown in this plot, achieves recognition rates

above 0.94, thereby signiﬁcantly outperforming both

of these classic approaches.

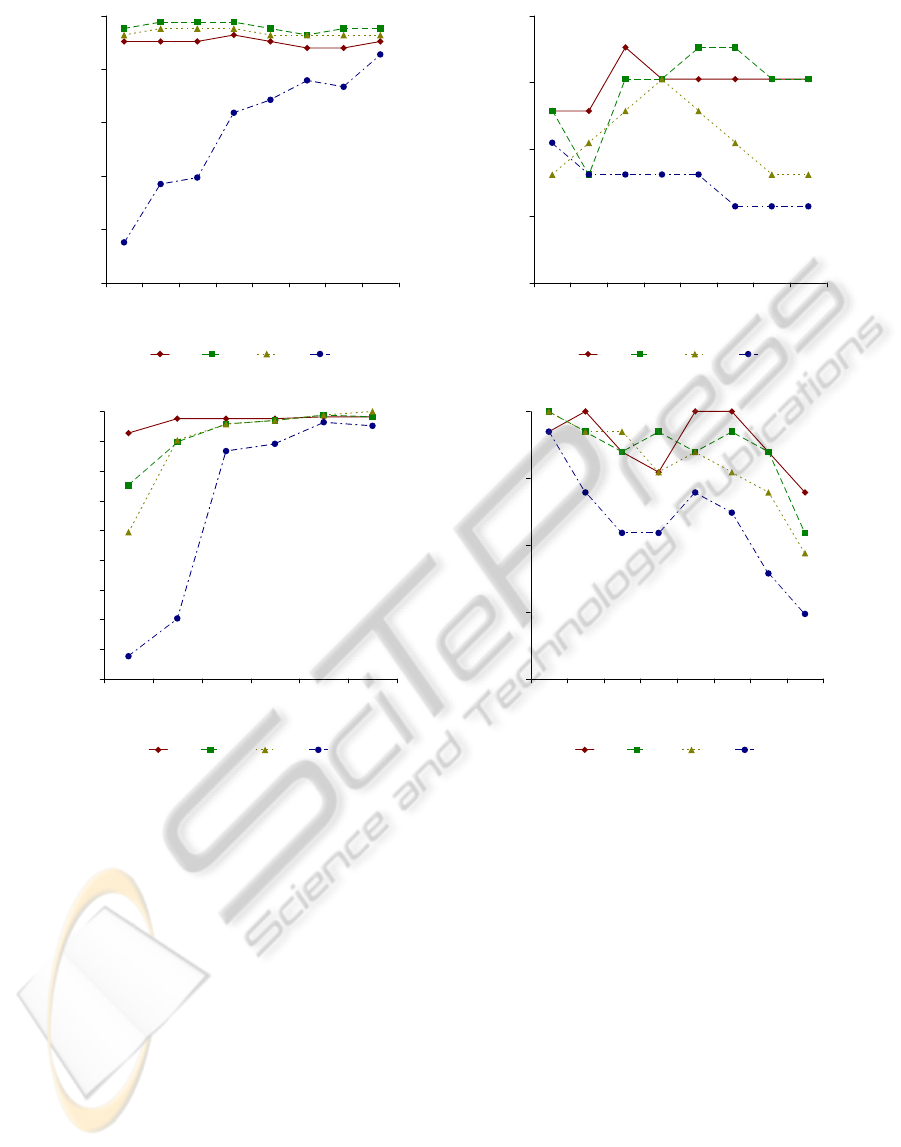
As part of a second experiment, the new GDD is

tested against the LARK, SSLD and DCT descriptors

in four different scenarios, the results of which are

seen in Figure 3. In each test, the three competing

descriptors are each individually substituted for the

GDD in the modiﬁed GHT algorithm.

The four descriptors are ﬁrst tested over the 165

images of the database using different patch sizes. Ex-

act patch sizes range from 7×7 to 35×35. The results

of this ﬁrst test are depicted in the plot of Figure 3(a).

The recognition rate of each of the GDD, LARK and

SSLD descriptors is more or less constant, regardless

of the patch size. The performance of the DCT, con-

versely, improves as the patch size increases.

In the second scenario, the results of which are

seen in Figure 3(b), the Canny edge threshold (Canny,

1986) is progressively increased. This threshold indi-

rectly determines the number of face traits that are

retained. As the threshold drops, more details are re-

tained. All four descriptors show varying degrees of

performance as this threshold changes, with the GDD

showing generally the best performance. The perfor-

mance of the LARK descriptor appears to improve

as the threshold increases. Conversely, the perfor-

mance of the DCT descriptor drops as the threshold

rises. Lastly, the SSLD seems to work best for a sin-

gle threshold, namely 0.35, with poorer performance

observed for both larger and smaller thresholds.

There are noticeable differences in the perfor-

mance of each of the three competing descriptors

as the epsilon threshold ε changes, as one can see

from Figure 3(c). Perhaps most exciting, the GDD

shows similar performance regardless of the partic-

ular choice of ε. The other three generally show

lower performance for smaller thresholds. Should the

threshold be lowered too much, however, it will often

be the case that δ 6< ε. This means that there will be

far fewer votes, thereby resulting in a lower recogni-

tion rate, regardless of the descriptor used.

Lastly, the performance of the four descriptors is

compared as the number of bins changes. The results

of this ﬁnal experiment are seen in Figure 3(d). The

recognition rate of the GDD is slightly above those

of the others. In all cases, though, the recognition

rate more or less falls as the number of bins increases.

When there are too many bins, the exact measure of

the gradient angle φ tends to play a very important

role. When there are fewer such bins, the recognition

rate is noticeably higher, as small variations in this an-

gle become more or less negligible. In the example of

Figure 3(d), a value of 20 leads to very good recogni-

tion rates. As a rule, the number of bins determines

the maximum allowable difference between the an-

gles φ of the edges in a given bin. If there are, again,

20 bins, then the maximum allowable difference is

equal to 360

◦

/ 20 = 18

◦

. If, however, there are many

more bins, 180 perhaps, then this difference decreases

to only 360

◦

/ 180 = 2

◦

. Having fewer bins has the

advantage of making the method more robust to de-

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

0.75

0.80

0.85

0.90

0.95

1.00

7 11151923273135

PATCH SIZE

RECOGNITION RATE

GDD LARK SSLD DCT

(a)

0.92

0.94

0.96

0.98

1.00

0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55

CANNY THRESHOLD

RECOGNITION RATE

GDD LARK SSLD DCT

(b)

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.80

0.90

1.00

0.0001 0.0010 0.0050 0.0100 0.0500 0.1000

EPSILON THRESHOLD

RECOGNITION RATE

GDD LARK SSLD DCT

(c)

0.92

0.94

0.96

0.98

1.00

15 30 45 60 75 90 120 180

NUMBER OF BINS

RECOGNITION RATE

GDD LARK SSLD DCT

(d)

Figure 3: Performance comparisons of GDD, LARK, SSLD and DCT descriptors under varying conditions (originals in

color); (a) varying patch size; (b) varying Canny threshold; (c) varying epsilon ε threshold; (d) varying number of bins.

formations and afﬁne transformations. On the other

hand, it increases the computational complexity as

there are more descriptors in each bin, which means

that more comparisons between descriptors have to be

performed.

4 CONCLUSIONS

This research uses a modiﬁed variant of the GHT to

address the problem of face recognition. It also makes

use of a new image descriptor. One of the most signif-

icant advantages of the modiﬁed GHT is the fact that

it does not require any training data. Moreover, it has

the ability to handle partial occlusions, changes in il-

lumination and small deformations. Additionally, this

algorithm can be upgraded as new descriptors become

available.

A number of future directions are presently being

explored. First, the method will be tested over sev-

eral additional databases, such as the well-known la-

beled faces in the wild (Huang et al., 2007) database.

These databases present new challenges, speciﬁcally

ones relating to image alignment, cropping and back-

ground removal. As well, the modiﬁed GHT will be

compared with other techniques beyond just Eigen-

faces and Fisherfaces. Enhancements include, for ex-

ample, adding a set of attribute classiﬁers (Kumar

et al., 2009) to reduce the number of images in a

database that need to be considered. These classiﬁers

would allow the method to rule out certain faces based

on gender, race, age, hair color or other attributes. En-

suring the proper alignment of faces in a database is

another major concern. In addition to the GDD, one

FaceRecognitionusingModifiedGeneralizedHoughTransformandGradientDistanceDescriptor

might also look at the Weber local descriptor (Chen

et al., 2010) (WLD). It is based on the Weber-Fechner

law (Winkler, 2005), which states that humans per-

ceive patterns according not only to changes in the

intensity of a stimuli, but also the initial intensity of

a stimuli. Additional descriptors worthy of study in-

clude those based on image histograms, ones that cap-

ture local shape information. Another powerful de-

scriptor is presented in (Cheng et al., 2008). It is

robust to non-rigid, afﬁne and other synthetic defor-

mations. With different descriptors having their own

unique advantages, it might also be useful to com-

bine multiple descriptors, with each encoding differ-

ent characteristics of a face image. Lastly, the task

of identifying multiple faces in an image could be

tackled using the Hough forests method described in

(Barinova et al., 2012). Another means of handling

multiple faces is to employ a face detection algorithm

as part of a preprocessing stage. Later, only those

faces actually detected would be considered by the

modiﬁed GHT.

REFERENCES

Anelli, M., Cinque, L., and Sangineto, E. (2007). Deforma-

tion tolerant generalized Hough transform for sketch-

based image retrieval in complex scenes. Image and

Vision Computing, 25(11):1802–1813.

Ballard, D. (1981). Generalizing the Hough transform to de-

tect arbitrary shapes. Pattern Recognition, 13(2):111–

122.

Barinova, O., Lempitsky, V., and Kohli, P. (2012). On detec-

tion of multiple object instances using Hough trans-

forms. Proc. IEEE Conf. Computer Vision and Pattern

Recognition, pages 2233–2240.

Belhumeur, P., Hespanha, J., and Kriegman, D. (1997).

Eigenfaces vs. Fisherfaces: Recognition using class

speciﬁc linear projection. IEEE Trans. Pattern Analy-

sis and Machine Intelligence, 19(7):711–720.

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Trans. Pattern Analysis and Machine

Intelligence, 8(6):679–698.

Chen, J., Shan, S., He, C., Zhao, G., Pietik

a, M., Chen,

X., and Gao, W. (2010). WLD: A robust local image

descriptor. IEEE Trans. Pattern Analysis and Machine

Intelligence, 32(9):1705–1720.

Cheng, H., Liu, Z., Zheng, N., and Yang, J. (2008). A de-

formable local image descriptor. Proc. IEEE Conf.

Computer Vision and Pattern Recognition, pages 1–8.

Duda, R., Hart, P., and Stork, D. (2001). Pattern Classiﬁca-

tion. John Wiley & Sons, 2nd edition.

Gall, J. and Lempitsky, V. (2009). Class-speciﬁc Hough

forests for object detection. Proc. IEEE Conf. Com-

puter Vision and Pattern Recognition.

Gonzalez, R. and Woods, R. (2002). Digital Image Process-

ing. Prentice Hall, 2rd edition.

Goshtasby, A. (2012). Image Registration: Principles,

Tools and Methods. Springer-Verlag.

Huang, G., Ramesh, M., Berg, T., and Learned-Miller, E.

(2007). Labeled Faces in the Wild: A Database for

Studying Face Recognition in Unconstrained Environ-

ments. Retrieved November 14, 2012, from http://vis-

www.cs.umass.edu/lfw/.

Kumar, N., Berg, A., Belhumeur, P., and Nayar, S. (2009).

Attribute and simile classiﬁers for face veriﬁcation.

Proc. IEEE Int. Conf. Computer Vision, pages 365–

372.

Li, M.-J. and Dai, R.-W. (1995). A personal handwritten

Chinese character recognition algorithm based on the

generalized Hough transform. Proc. Int. Conf. Docu-

ment Analysis and Recognition, 2:828–831.

Li, Q. and Zhang, B. (2005). Image matching under gen-

eralized Hough transform. Proc. IADIS Int. Conf. Ap-

plied Computing, pages 45–50.

Li, S. and Jain, A., editors (2011). Handbook of Face

Recognition. Springer-Verlag, 2nd edition.

Moise, M. (2012). A New Approach to Face Recogni-

tion Based on Generalized Hough Transform and Lo-

cal Image Descriptors. Master’s thesis, University of

Regina, Regina, Saskatchewan, Canada.

Schneider, J. and Borlund, P. (2007). Matrix comparison,

Part 1: Motivation and important issues for measuring

the resemblance between proximity measures or ordi-

nation results. Jour. American Society for Information

Science and Technology, 58(11):1586–1595.

Schubert, A. (2000). Detection and tracking of facial

features in real time using a synergistic approach

of spatio-temporal models and generalized Hough-

transform techniques. Proc. IEEE Int. Conf. Auto-

matic Face and Gesture Recognition, pages 116–121.

Seo, H. and Milanfar, P. (2009). Nonparametric detection

and recognition of visual objects from a single exam-

ple. Workshop on Defense Applications of Signal Pro-

cessing.

Seo, H. and Milanfar, P. (2011). Face veriﬁcation using

the LARK representation. IEEE Trans. Information

Forensics and Security, 6(4):1275–1286.

Seo, H. J. and Milanfar, P. (2010). Training-free, generic

object detection using locally adaptive regression ker-

nels. IEEE Trans. Pattern Analysis and Machine In-

telligence, 32(9):1688–1704.

Shechtman, E. and Irani, M. (2007). Matching local self-

similarities across images and videos. IEEE Conf.

Computer Vision and Pattern Recognition, pages 1–8.

Turk, M. and Pentland, A. (1991). Eigenfaces for recogni-

tion. Jour. Cognitive Neuroscience, 3(1):71–86.

Winkler, S. (2005). Digital Video Quality: Vision Models

and Metrics. John Wiley & Sons.

Yale (1997). Yale Face Database. Retrieved July

4, 2012, from http://cvc.yale.edu/projects/yalefaces/

yalefaces.html.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods