
The State of the Art in the Development of a Versatile Argumentation
System based on the Logic of Multiple-valued Argumentation
Satoru Tannai
1
, Shogo Ohta
1
, Takeshi Hagiwara
2
, Hajime Sawamura
2
and Jacques Riche
3
1
Graduate School of Science and Technology, Niigata University, Niigata, Japan
2
Institute of Science and Technology, Niigata University, Niigata, Japan
3
Department of Computer Science, Katholieke Universiteit Leuven, Leuven, Belgium
Keywords:
Multiple-valued Argumentation, Neural Net Argumentation, Eastern argumentation, Syncretic Argumenta-
tion, Argument Mining, Argument Animation.
Abstract:
This paper reports on the state of the art in the development of a versatile argumentation system in which
various auxiliary features for argumentation are incorporated. Such an argumentation system was built on our
underlying argumentation system, LMA: the Logic of Multiple-valued Argumentation, aiming at promoting
our understanding of argumentation processes. We in particular present some very new and unique aspects of
computational argumentation: the syncretic argumentation, the argument mining and frequent sub-argument
discovery, the argument metamorphosis from symbol to animation via natural language, Easternargumentation
based on Indian logic, and the argumentation based on symbolism and connectionism. Such a hybridization
of various features would broaden the scope of the applications of computational argumentation in various
ways.
1 INTRODUCTION
Argumentation is a dialectical process of knowing
things (inquiry) and justifying them (advocacy) in
general. Significances of argumentation have been
recently recognized, and logical models of it have
emerged as a promising paradigm for modeling agent
reasoning and communication in light of interac-
tion with other agents and arguments. Among other
things, it has such a nature that closely mirrors the
way humans reason and hence provides us a general
framework for inference and decision making in the
presence of inconsistent, uncertain and incomplete in-
formation.
We have developed a computational argumenta-
tion framework that basically consists of EALP and
LMA (Takahashi and Sawamura, 2004). EALP (Ex-
tended Annotated Logic Programming) is an expres-
sive logic programming language we formalized for
argumentation. The basic language constituents are
literals associated with annotations as truth-values
or epistemic states of agents. LMA is a Logic of
Multiple-valued Argumentation constructed on top of
EALP. It has three notions of negation to yield a mo-
mentum or driving force for argumentation. LMA
is a generic logic of multiple-valued argumentation
that allows us to specify various types of truth val-
ues depending on application domains, and to deal
with uncertain arguments. Such a feature brings us
the extensive applicability of LMA that is considered
the most advantageous point in comparison to other
approaches to argumentation (Rahwan and Simari,
2009).
This paper reports on the state of the art in the
development of a versatile argumentation system in
which various auxiliary features for argumentation
are incorporated on top of EALP/LMA, aiming at
promoting our understanding of argumentation pro-
cesses. We in particular present some very new and
unique aspects of computational argumentation: the
syncretic argumentation, the argument mining and
frequent sub-argument discovery, the argument meta-
morphosis from symbol to animation via natural lan-
guage, Eastern argumentation based on Indian logic,
and the argumentation based on symbolism and con-
nectionism. Such a hybridization of various features
would broaden the scope of the applications of com-
putational argumentation in various ways.
The paper is organized as follows. In the next sec-
tion, we briefly illustrate part of EALP and LMA.
In Section 3, we present an overall picture of IAE
(Integrated Argumentation Environment) for arguing
217
Tannai S., Ohta S., Hagiwara T., Sawamura H. and Riche J..
The State of the Art in the Development of a Versatile Argumentation System based on the Logic of Multiple-valued Argumentation.
DOI: 10.5220/0004198902170224
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 217-224
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

agents on the Internet, augmented with various aux-
iliary features: the syncretic argumentation, the ar-
gument mining and frequent sub-argument discov-
ery, the argument metamorphosis from symbol to an-
imation via natural language, Eastern argumentation
based on Indian logic, and the argumentationbased on
symbolism and connectionism. In the succeeding sec-
tions, we briefly describe those features one by one.
The final section includes concluding remarks and fu-
ture work.
2 OUTLINE OF EALP AND LMA
2.1 Knowledge Representation and
Argument in EALP and LMA
EALP (Extended Annotated Logic Programming) is
an extended version of the Annotated Logic Program-
ming (ALP) (Schweimeier and Schroeder, 2005) by
introducing the extra negations below. Suppose the
followings are knowledge bases that agent A and B
have for argumentation respectively.
AgentA :
climb(satoru, mountain) : 0.9 ← reflesh(satoru) : 0.8.
reflesh(satoru) : 0.9 ← true.
AgentB :
∼ climb(satoru, mountain) : 0.6
← not ∼ get tired from(satoru, walking) : 0.8.
Real values are annotations for literals. They rep-
resent degrees of agents’ beliefs. For example, we
could read climb(satoru, mountain) : 0.9 as ‘Satoru
surely climb mountain.’ The symbol ∼ stands for
explicit negation (Takahashi and Sawamura, 2004).
We could read ∼ climb(satoru, mountain) : 0.6
as ‘Satoru possibly does’t climb mountain.’ The
symbol not stands for default negation (Takahashi
and Sawamura, 2004). We could read not ∼
get tired f rom(satoru,walking) : 0.8. as ‘There is no
evidence for now to show that Satoru does’t get tired
from walking.’
An argument is a list of rules (knowledge). For
example, the following Arg can be an argument, since
the truth degree 0.9 is greater than 0.8, or put it differ-
ently, the truthfood of reflesh(satoru) : 0.9 includes
that of reflesh(satoru) : 0.8.
Arg = [climb(satoru,mountain) : 0.9← reflesh(satoru) :
0.8., reflesh(satoru) : 0.9 ← true.]
The head of a rule is called a conclusion of the rule,
and the annotated default literals in the body of the
rule is called assumptions of the rule. We write
concl(Arg) for the set of conclusions and assm(Arg)
for the set of assumptions of the argument Arg.
An argumentation is a finite nonempty sequence
of moves move
i
= (Player
i
, Arg
i
)(i > 0) that meets
the following conditions.
1. Player
i
= P iff i is odd; and Player
i
= O iff i is
even.
2. If Player
i
= Player
j
= P and i 6= j, then Arg
i
6=
Arg
j
.
3. If i ≥ 2, then Arg
i
defeats Arg
i−1
.
2.2 Judgement of Winning Dialogues
In LMA, whether an agenda of argumentation is justi-
fied or not is judged based on the grounded semantics
in Dungean semantics (Dung, 1995). In particular,
the results of argumentation are displayed as dialogue
trees based on the dialectical proof theory that corre-
sponds to the grounded semantics (Schweimeier and
Schroeder, 2005). A dialogue tree is a tree in which
the node of the tree represents an argument and the
branch of the tree represents an attack relation (Taka-
hashi and Sawamura, 2004). A winning dialogue tree
is a kind of dialogue tree in which every path in it is
ended by the proponent’s move (P), and an agenda is
justified if and only if at least one winning dialogue
tree exists.
3 A VERSATILE IAE
3.1 Integrated Argumentation
Environment (IAE)
From this section, we will propose a more versatile
argumentation system in which various auxiliary fea-
tures for argumentation are incorporated on top of
LMA. For this, the following features are considered
and realized to support or extend the past LMA argu-
mentation (see Fig. 2 for the overall architecture of
the integration).
(1) The hybrid argumentation based on symbolism
and connectionism (Makiguchi and Sawamura, 2007)
(Gotou et al., 2011)
We constructed a neural network that can compute
the full Dungean semantics such as the stable, pre-
ferred, complete extension in addition to the grounded
extension (Dung, 1995) which the original LMA only
dealt with.
In Section 4, we briefly outline our neural network
argumentation.
(2) The Eastern argumentation (Sawamura et al.,
2005)
We considered a significant specialization of
LMA to Tetralemma F O U R = {⊥, t,f, ⊤} with an
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
218

Figure 1: Argumentation graph of TPP, where the blue and red boxes denote arguments put forward, with the blue ones by
the proponent side and the red ones by opponent side. The contents of the actual arguments pop up by clicking the nodes.
Figure 2: An overall picture of LMA-based argumentation
system integrated with various auxiliary features.
Eastern mind, and confirm its expressiveness and ap-
plicability by applying it to arguments involving in
Eastern thought and philosophy. We showed that
LMA allows for a kind of pluralistic argumentation,
or a fusion of Eastern and Western argumentation
through cultural argument examples.
In Section 5, we, in particular, describe another
kind of the Eastern argumentation and its seman-
tics computation by the neural network argumentation
mentioned (1) above.
(3) The syncretic argumentation based on LMA
(Maruyama et al., 2012)
The syncretic argumentation framework is one
that agents with different epistemology can engage in
argumentation, taking into account the Golden Rule
in the ethics of reciprocity and Confucius’s Golden
Rule. For example, back to the ancient, let us con-
sider such a scene that Aristotle and Lao Tzu en-
counter, and argue about a proposition p. Perhaps,
Aristotle might say p is definitely true with his two-
valued epistemology T W O = {f, t}, and Lao Tze
might say p may hold with truth degree ⊥ with his
four-valued epistemology F O U R = {⊥, t, f, ⊤}. Af-
ter all, they turn out to know that they can not com-
municate with each other. This is not just a matter of
difference of knowledge, but difference of a way of
recognizing things (epistemology), world-view, logic,
and so on.
For the syncretic argumentation, we devised three
kinds of lattice operations: homomorphism, fusion
and sum that are to be described in Section 6.
(4) The frequentsub-argument mining and discov-
ery (Seino et al., 2011)
Frequent sub-tree mining is useful since it enables
agents to prepare or discover meaningful knowledge
to be used for argumentation (Seino et al., 2011).
For this, we employed the frequent subtree mining
algorithm SLEUTH (Zaki, 2005) since it allows to
mine embedded and induced subtrees which turn out
to bring useful and meaningful substructures (sub-
arguments) from argument databases to us. More in
Section 7.
(5) Argument animation: the argument metamor-
phosis from symbol to animation via natural language
(Narita and Sawamura, 2008)
Imaging of information is an effective way to as-
sist us in easy and quick acquisition and understand-
ing of information with personal sense organ. We
demonstrated the way for imaging arguments among
agents using the outcomes of LMA. It starts from a
simple argument scenario with logical formulas pro-
duced by the dialectical proof theory of LMA. Then, it
transforms to the natural language representation that
is augmented with action and emotion of agents, and
finally to a moving image of the resulting natural lan-
guage scenario. Such an attempt might lead to a new
approach to an electronic scenario writer and auto-
matically creating moving images content. More in
Section 8.
There has been no argumentation system so far
like our versatile one in which those features con-
cerned with argumentation are considered and inte-
grated. In what follows, we will describe these fea-
tures in more detail one by one.
3.2 Case Studies
We applied IAE to a somewhat realistic social issue:
‘Should we join TPP:Trans-Pacific Partnership’. The
TheStateoftheArtintheDevelopmentofaVersatileArgumentationSystembasedontheLogicofMultiple-valued
Argumentation
219

result of the argumentation is displayed as a dialogue
tree (see Fig. 1). This is not a winning dialogue tree.
However, we may analyze our argument and build a
winning dialogue tree through this dialogue tree, that
is, by knowing weak points of our argument, supple-
menting more knowledge to agents, and so on. Later
we will describe how to do it by our argument mining
techniques.
4 NEURAL NETWORK
ARGUMENTATION
The past IAE computed only the grounded semantics
for argumentation (Takahashi and Sawamura, 2004).
In order to allow to compute other Dungean se-
mantics, we constructed a simple but versatile neu-
ral network for neural network argumentation, so
that it can decide which argumentation semantics
(admissible, stable, semi-stable, preferred, complete,
and grounded semantics) a given set of arguments
falls into, and compute argumentation semantics via
checking (Gotou et al., 2011). Furthermore, we
showed that such a neural network allows for the
opposite direction from neural network computation
to symbolic argumentation/dialogue (Gotou et al.,
2011). In fact, We dealt with the question how various
argumentation semantics can have dialectical proof
theories, and described a possible answer to it by ex-
tracting or generating symbolic dialogues from the
neural network computation under various argumen-
tation semantics.
We will not describe the technical details for con-
structing a neural network for argumentation and its
computing method in this paper (see (Goto et al.,
2011) for them). Instead, we illustrate our basic
ideas by using a simple argumentation graph and il-
lustrating a neural network translated from it. We
assume readers are familiar with the Dungean se-
mantics such as admissible, stable, semi-stable, pre-
ferred, complete, and grounded semantics (Caminada,
2006)(Dung, 1995).
4.1 Example of the Dungean Semantics
Computed by the Neural Network
in IAE
Figure 3 shows a financial argument example com-
puted by the neural network argumentation from the
following arguments, where the first argument, for
example, is a counterpart of the statement ’Spain is
not Greece’, asserting that Spain blames that Greece’s
financial situation is not sound as Spain believes that
there is no evidence to show it’s ill financial situation.
A = [∼ greece : 1.0 ← not ∼ spain : 1.0]
B = [∼ greece : 1.0 ← not ∼ portugal : 1.0]
C = [∼ ireland : 1.0 ← not ∼ greece : 1.0]
D = [∼ ireland : 1.0 ← not ∼ spain : 1.0], [∼
portugal : 1.0 ← not ∼ spain : 1.0]
E = [∼ greekterritory : 1.0 ← not ∼ ireland : 1.0]
F = [∼ ireland : 1.0 ← not ∼ spain : 1.0& not ∼
portugal : 1.0]
G = [∼ spain : 1.0 ← not ∼ italy : 1.0]
H = [∼ uganda : 1.0 ← not ∼ spain : 1.0]
I = [∼ spain : 1.0 ← not ∼ uganda : 1.0]
Figure 3: Financial argument by the neural network argu-
mentation.
The argument engine constructed by the neural
network has been shown to be useful since it allows to
compute every Dungean semantics in a uniform man-
ner. It is not simply a yet another alternative engine
for argumentation. It plays an important role as the
IAE argument engine.
5 EASTERN ARGUMENTATION
BASED ON INDIAN-LOGIC
Truth is relative to culture (pluralism in philosophy)
and can be brought through argumentation which is a
true figure of logic (argumentation vs. logic). On the
basis of this view or recognition, we have taken into
account not only Western argumentation and logic but
also Eastern argumentation and logic. In this sec-
tion, we give an Eastern argumentation model and its
adaptation to IAE. In particular, we adopt a typical
way of thinking in the Indian logic, ”five-membered
syllogism (argument schema)” (Ganeri, 2001)(Ma-
halakshmi and Geetha, 2009), to our argumentation
model. It is expected that it results in arguments
with higher persuasion than western argumentation
and logic only.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
220

5.1 Five-membered Syllogism
According to the ancient Indian logic, the proper for-
mulation of the inference should have five parts. It
is technically known as the five-membered inference
or argument schema. According to Nyaya Sastra, an
inferential proof is made up from the following mem-
bers:
1. The statement
2. The cause or reason for the statement
3. The example (metaphor expression)
4. The application of that example
5. The conclusion
An example of the five-membered syllogism is as fol-
lows. (1) This hill has fire (statement), (2) Because, it
has smoke (reason), (3) Since whatever has smoke has
fire, e.g. an oven (example), (4) This hill has smoke,
which is associated with fire (application), (5) There-
fore, this hill has fire (conclusion)
5.2 Eastern Argumentation Model
Taking into account the five-membered syllogism,
we construct an Eastern argumentation model in
which attack relations are redefined so that the five-
membered syllogism may stand on predominance
compared with other argument by considering ‘per-
suasive power of statement’. In doing so, we in-
troduce ‘inductive clause’ that can be included only
in Eastern knowledge, and also specifies that the de-
gree of predominancechanges with examples used for
Eastern arguments.
5.2.1 An Inductive Clause (Indian Induction)
The five-membered syllogism can be captured in
terms of EALP as follows.
A : µ
3
← invariable(B, A) : µ
2
&
B : µ
1
.
invariable(B, A) : µ
2
← ind(example) : α.
B : µ
1
← true.
Then the example of the five-membered syllogism
mentioned above is expressed as follows.
has(hill, fire) : 1.0 ← invariable(smoke, fire) : 1.0
&
has(hill, smoke) : 1.0.
invariable(smoke, fire) : 1.0 ← ind(oven) : α.
has(hill, smoke) : 1.0 ← true.
where, the inductive clause, ind(oven) : α plays the
roles of the third member of the five-membered syl-
logism: The example (metaphor expression) and the
fourth member of the five-membered syllogism: The
application of that example. Accordingly to the spe-
cific notations introduced, attack relations for argu-
ments deserve to be changed so that eastern argu-
ments may become advantageous by the relation be-
tween this α and annotations as truth values µ of other
literals. The details are, however, omitted in this pa-
per.
5.2.2 Illustrative Example
We illustrate a simple example of an Eastern argu-
ment. Suppose we have the following argumentation
framework:
AF
1
=< {A, B,C, D, E, F, G, H, I, J}, {(A, E), (B,C),
(C, A), (C, D), (D,C), (E, A)} > .
Then we have the following extensions.
− Complete extension : {B, D, F, G, H, I, J},
{A, B, D, F, G, H, I, J}, {B, D, E, F, G, H, I, J}
− Stable extension : {A, B, D, F, G, H, I, J},
{B, D, E, F, G, H, I, J}
− Grounded extension : {B,D, F, G, H, I, J}.
However, if we have the following framework in
which the attack relation (E, A) in AF
1
is blocked by
the Eastern attack relation,
AF
2
=< {A, B,C, D, E, F, G, H, I, J}, {(A, E), (B,C),
(C, A), (C, D), (D,C)} >
then, we turn to have the following extensions.
− Complete extension : {A, B, D, F, G, H, I, J}
− Stable extension : {A, B, D, F, G, H, I, J}
− Grounded extension : {A,B, D, F, G, H, I, J}.
These computations have been done by the neural
network argumentation of IAE.
6 SYNCRETIC
ARGUMENTATION
We considered a novel approach to argumentation,
called syncretic argumentation that allows agents to
participate in argumentation even if they have knowl-
edge bases with their own annotations as truth-values
that reflect agents epistemic states of propositions.
For the syncretic argumentation,we devised three
methods: the lattice homomorphism, the fusion of lat-
ices, and the sum of lattices.
6.1 The Lattice Homomorphism
The mathematical structure of annotations in LMA is
a complete lattice and the homomorphism is a mathe-
matical apparatus convenient to syncretize the differ-
ence of epistemic states of propositions. It guarantees
agents to retain agents’ epistemic structure when em-
bedding one lattice to the other. We also considered
the bi-directional homomorphism on lattices since it
allows for a fair, unbiased and pluralistic argumenta-
tion, prohibiting unilateral one.
TheStateoftheArtintheDevelopmentofaVersatileArgumentationSystembasedontheLogicofMultiple-valued
Argumentation
221

Let us consider two typical lattices: the two-
valued complete lattice T W O and the four-valued
one F O U R . The former is typical in the West,
and the latter in the early philosophical litera-
ture and text of Buddhism (Sawamura and Mares,
2004). T W O =< { f, t}, ∨, ∧, ≤>, where f ≤ t,
and F O U R =< {⊥, t, f, ⊤}, ∨, ∧, ≤>, where ∀x,y ∈
{⊥, t, f, ⊤} x ≤ y ⇔ x = y ∨ x = ⊥ ∨ y = ⊤. Note
that we associate the suffix with annotations to avoid
ambiguity of the same annotation names, that is, t
2
represents the annotation t in T W O and t
4
represents
the annotation t in F O U R , for example.
Figure 4: Lattice homomorphism.
6.2 The Fusion of Lattices
It is induced through the lattice product, and can be
considered as providing a natural way to syncretize
the difference of epistemic states of propositions. The
fusion of lattices is formally defined(Maruyama et al.,
2012).
Our approach to syncretic argumentation has such
advantages as majority principle, order preserving
and commutativity. Fig. 5 shows the fusion of T W O
and F O U R .
Figure 5: Fusion of T W O and F O U R .
6.3 The Horizontal Sum of Lattices
The following is one of the lattice sum operations,
called the horizontal sum of lattices (Davey and
Priestley, 2002).
The syncretism by the lattice sum keeps the lat-
tice structure of each agent intact, only identifying the
minimal and maximal elements of it with those of the
common ground. This better serves to act as a brake
on excessive conflicts among agents. It is so-called a
peaceful syncretic argumentation. Fig. 6 is the hori-
zontal sum of T W O and F O U R .
Using either of these methods for the syncretic
argumentation, agents get to communicate and enter
their argumentation process.
Figure 6: Horizontal sum of T W O and F O U R .
7 ARGUMENT MINING
The roles of argument mining for IAE development
are twofold. As illustrated in Fig2, it helps the knowl-
edge preparation in the process of IAE as agents want
to collect their own knowledge for argumentation that
are hopefully more efficient and persuasive, and fur-
thermore generally approved. The other is that when
an argument has not been justified, agents might want
to analyze and turn it to a justified one with help of
mined arguments that are resistant enough for coun-
terarguments. Fortunately we now live in the world
full of information, in particular, information of argu-
ment form, which are ceaselessly produced every day
of our lives not only in the traditional media but also
in the social WEB like Twitter, Facebook, SNS and
many others. Such a ‘Big Data’ has become so valu-
able that it is deemed a new class of economic asset,
such as oil.
7.1 Argument Data Preparation
A (reasonable) argument is a tree whose top leaves
are premises and assumptions, and root is a conclu-
sion, just like a (formal) proof. The argument data
for argument mining consists of such argument trees.
Contemporary argument data source largely comes
from the social Web such as SNS, Blog, Twitter, etc.,
and are written in natural languages. So, we em-
ployed Araucaria (Reed and Rowe, 2004)(Araucaria,
2008) which is an argument mapping tool for ana-
lyzing, diagramming and representing arguments, for
the data preparation of our argument mining. One
of the unique features in Araucaria is that analyzed
arguments can be saved in a portable format called
AML (Argument Markup Language) that is a special
XML stipulated in the document type definition, ar-
gument.dtd, particularly designed for arguments.
7.2 Frequent Subtree Mining
The frequent subtree mining is in general one of NP
problems. The number of induced or embedded sub-
trees for a labeled tree T grows exponentially with
the size of T. Various frequent subtree mining algo-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
222
rithms, therefore, have been proposed so far, corre-
sponding with targeted tree database types and sub-
structure types to be discovered. In this paper, we
employed SLEUTH algorithm (Zaki, 2005) for our
purpose since the input of this algorithm is a set of
unordered trees, the output is embedded subtrees, and
it has the option for induced subtrees as well.
In our former paper (Seino et al., 2011), we
showed that the so-called proof by contradiction
(PBC, reductio ad absurdum) is mined from a formal
proof data base. The assumption and conclusion of
PBC are in the ancestor relationship.
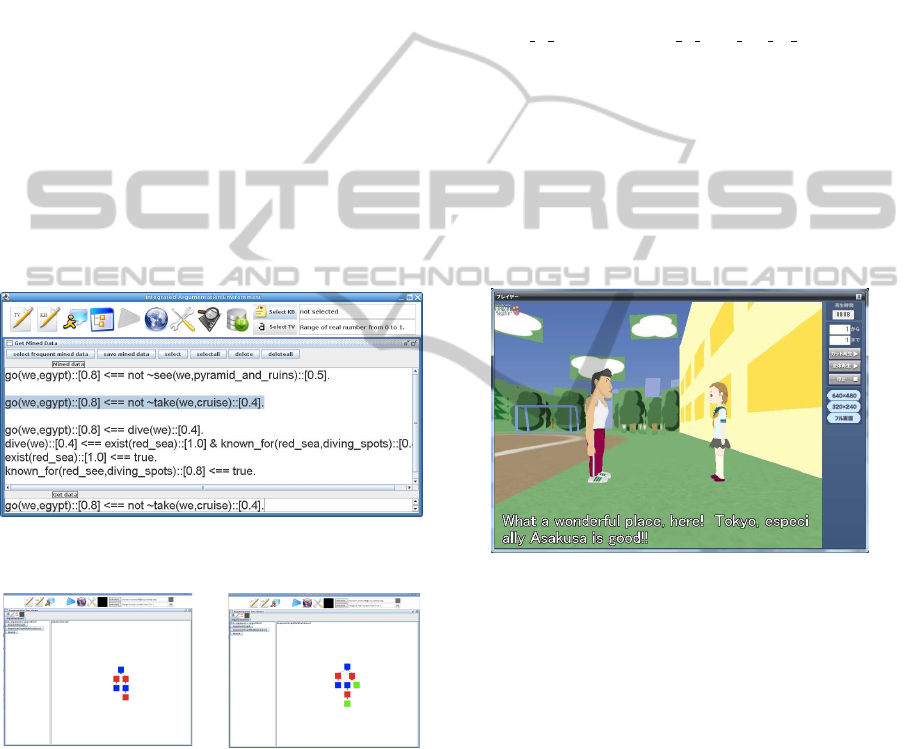
In addition, we applied the frequent argument
mining to the knowledge discovery for unjustified ar-
guments. Fig. 7 is a screenshot of IAE that dis-
plays mined knowledge on the upper pane and se-
lected knowledge from among it by a user on the
lower pane. Fig 8 is a screenshot of an argument
graph on an argument at the top node in which it is
not justified, and Fig 9 is a screenshot of an argument
graph with some arguments added by the argument
mining, where the argument turns out to be justified.
Figure 7: Knowledge extraction by the frequent argument
mining.
Figure 8: Argument graph
without justification.
Figure 9: Argument graph
with justification by argu-
ment mining.
8 ARGUMENT ANIMATION
IAE can be viewed as a scenario writer since it
can produce an argumentative dialogue done among
agents. We have been further promoting this observa-
tion to argument animation (Narita and Sawamura,
2008), (DMD, 2008). The way to this consists of three
phases.
1. Producing a dialogue process in logical formulas
by IAE
2. Translating it to a natural language dialogue by a
simple language translation
3. Generating an animation script from it with the
help of humans.
For example, the following unscientific and em-
pirical but persuasive phrase in EALP
weather is good : 0.7 ← sky is dyed red by sunset : 0.8
is almost directly translated to
If the sky is considerably dyed red by sunset, the weather is
surely good
in the preparation of a corresponding list of annota-
tions and adverbs or adjectives. The third phrase can
be semi-automatically accomplished by using an an-
imation generation software that usually has a script
language proper to animation generation. Figure 10
shows one shot of an argument animation of an argu-
ment on a trip to Egypt.
Figure 10: A slot of an argument animation generated by
DMD.
9 CONCLUSIONS
In this paper,we have reported on the state of the art in
the development of a versatile argumentation system
based on the logic of multiple-valued argumentation.
The distinctive features of it are two-fold. One is that
its underlying theory is the logic of multiple-valued
argumentation with which uncertain arguments can be
dealt with under uncertain knowledge for argumenta-
tion. Such an argumentation model has been and still
is rare in the community of argumentation. The other
is that our argument system is versatile in the sense
that it is equipped with the following unexemplified
apparatuses:
• Hybrid argumentation based on symbolism and
connectionism
TheStateoftheArtintheDevelopmentofaVersatileArgumentationSystembasedontheLogicofMultiple-valued
Argumentation
223

• Eastern argumentation based on Indian logic
• Syncretic argumentation
• Argument mining based on the frequent sub-
argument mining and argument discovery
• Argument animation
These are aspects of argumentation in our argument
activities we meet in our daily life as well except the
first. Now we could say we have developeda very rich
argument system, compared with other works (Rah-
wan and Simari, 2009).
We will further develop the system to incorpo-
rate the shift from argumentation to dialogue and the
learning triggered by argumentation.
REFERENCES
Araucaria (2008). Araucaria version3.1-USER MANUAL-.
Caminada, M. (2006). Semi-stable semantics. In Dunne,
P. E. and Bench-Capon, T. J. M., editors, Computa-
tional Models of Argument: Proceedings of COMMA
2006, volume 144 of Frontiers in Artificial Intelli-
gence and Applications, pages 121–130. IOS Press.
Davey, B. A. and Priestley, H. A. (2002). Introduction to
Lattices and Order. Cambridge.
DMD (2008). Digital Movie Director.
http://www.
movie-school.org/
.
Dung, P. (1995). On the acceptability of arguments and its
fundamental role in nonmonotonic reasoning, logics
programming and n-person games. Artificial Intelli-
gence, 77:321–357.
Ganeri, J. (2001). Indian Logic. Curzon Press.
Goto, Y., Hagiwara, T., and Sawamura, H. (2011). Neural
networks computing the dungean semantics of argu-
mentation. In NCTA 2011 - Proceedings of the Inter-
national Conference on Neural Computation Theory
and Applications, pages 5–14.
Gotou, Y., Hagiwara, T., and Sawamura, H. (2011). Ex-
tracting argumentative dialogues from the neural net-
work that computes the dungean argumentation se-
mantics. In 7th International Workshop on Neural-
Symbolic Learning and Reasoning(NESY2011). IEEE.
Mahalakshmi, G. S. and Geetha, T. V. (2009). An in-
dian logic-based argument representation formalism
for knowledge-sharing. Logic Journal of the IGPL,
17(1):55–76.
Makiguchi, W. and Sawamura, H. (2007). A hybrid ar-
gumentation of symbolic and neural net argumenta-
tion (part i, part ii). In Rahwan, I., Parsons, S., and
Reed, C., editors, ArgMAS, volume 4946 of Lecture
Notes in Computer Science, pages 197–215/216–233.
Springer.
Maruyama, Y., Hasegawa, T., Hagiwara, T., and Sawamura,
H. (2012). Syncretic argumentation for multi-agents
by lattice homomorphism, fusion and sum. In Argu-
mentation in Multi-Agent Systems, 8th International
Workshop, ArgMAS 2011, Revised Selected and In-
vited Papers, volume 7543 of Lecture Notes in Com-
puter Science, pages 46–65. Springer.
Narita, T. and Sawamura, H. (2008). An attempt to ar-
gument metamorphosis from symbols to moving im-
ages. In Proceedings of 2008 Joint Agent Symposium
(JAWS2008).
Rahwan, I. and Simari, G. R. E. (2009). Argumentation in
Artificial Intelligence. Springer.
Reed, C. and Rowe, G. (2004). Araucaria: Software for
argument analysis, diagramming and representation.
International Journal on Artificial Intelligence Tools,
13(4):983–.
Sawamura, H. and Mares, E. (2004). How agents should
exploit tetralemma with an eastern mind in argumen-
tation. In Mike Barley and Nik Kasabov (eds.): In-
telligent Agents and Multi-Agent Systems VII, Lec-
ture Notes in Artificial Intelligence, Springer, volume
3371, pages 259–278.
Sawamura, H., Takahashi, T., and Matsunaga, K. (2005).
An eastern specialization of logic of multiple-valued
argumentation to tetralemma originated in india. In
Prasad, B., editor, IICAI, pages 1274–1291. IICAI.
Schweimeier, R. and Schroeder, M. (2005). A parame-
terised hierarchy of argumentation semantics for ex-
tended logic programming and its application to the
well-founded semantics. TPLP, 5(1-2):207–242.
Seino, Y., Sawamura, H., and Hagiwara, T. (2011). Towards
argument mining. In Proceedings of 2011 Interna-
tional Conference on Data Engineering and Internet
Technology (DEIT 2011), pages 27–34. IEEE.
Takahashi, T. and Sawamura, H. (2004). A logic of
multiple-valued argumentation. In Proceedings of the
third international joint conference on Autonomous
Agents and Multi Agent Systems (AAMAS’2004),
pages 800–807. ACM.
Zaki, M. J. (2005). Efficiently mining frequent embedded
unordered trees. Fundam. Inform., 66(1-2):33–52.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
224
