3D Model Retrieval using Density-based Silhouette Descriptor
Qi Tang and Xin Yang
Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, Shanghai, China
Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China
Keywords:
Shape Matching, Retrieval, Silhouette, Probability Density Function, Kernel Density Estimation, Invariance.
Abstract:
In this paper we present a new content-based retrieval descriptor, density-based silhouette descriptor (DBS).
It characterizes a 3D object with multivariate probability functions of its 2D silhouette features. The new
descriptor is computationally efficient and induces a permutation property that guarantees invariance at the
matching stage. Also, it is insensitive to small shape perturbations and mesh resolution. The retrieval per-
formance on several 3D databases shows that the DBS provides state-of-art discrimination over a broad and
heterogeneous set of shape categories.
1 INTRODUCTION
With an increasing number of 3D repositories avail-
able on the Internet, effective retrieval from large
databases has become a hot spot (Marini et al.,
2007; Li et al., 2012). Text-based systems, requir-
ing manual annotation of the shapes, is severely lim-
ited in describing complicated 3D models (Tangelde
and Veltkamp, 2008). Content-based systems, on
the other hand, only require a shape descriptor that
can automatically extract shape features (Min et al.,
2004).
Among many content-based systems, Silhouette
descriptor (SIL) (Vranic, 2004) and Density-Based
Frame (DBF) (Akgul et al., 2009) have high retrieval
accuracy on a large number of databases. By intro-
ducing DBF into SIL, we proposed a new shape de-
scriptor, density-based silhouette descriptor (DBS). It
uses multivariate probability density functions to de-
scribe the feature distributions of a given 3D object’s
2D silhouettes. Like DBF, DBS is computationally ef-
ficient and enjoys a permutation property that guaran-
tees invariance to a certain class of 3D transformation
at the shape matching stage. Similar to SIL, DBS is
relatively insensitive to small shape perturbations and
mesh resolution. Consequently, DBS can be adapted
to a broad and heterogeneous set of shape categories.
The rest of this paper is organized as follows: Sec-
tion 2 describes the steps of DBS and its invariance
properties in detail. Following that, Section 3 under-
takes an exhaustive campaign of retrievalexperiments
and illustrates the effectiveness of DBS on several 3D
model databases. We draw conclusions in Section 4.
2 DENSITY-BASED SILHOUETTE
Let P
i
,i = 1, 2, 3 be the model’s one projection and
f(•|P
i
) be the probability density function of feature
distribution on projection P
i
. Let S be the random fea-
ture defined on the model’s 2D silhouettes and take
values within R
S
. The source set

s
i
k
∈ R
S

K
i
k=1
is fea-
ture values, computed on the projection P
i
, and is
used to estimate the probability function. Further-
more, we specify a finite set of N evaluation points,
{t
n
∈ R
S
}
N
n=1
, called target set. Thus, for an object O,
its density-based silhouette descriptor of feature S is
f
S|O
= [ f
S
(t
1
|P
1
),... , f
S
(t
N
|P
1
), f
S
(t
1
|P
2
),... ,
f
S
(t
N
|P
2
), f
S
(t
1
|P
3
),... , f
S
(t
N
|P
3
)] (1)
Density-based Silhouette consists of four main stages
(see Figure 1):
1. In the silhouette extraction stage, we extract 2D
silhouettes from a given 3D model and demon-
strate DBS’s insensitivity towards low mesh reso-
lution.
2. In the feature calculation stage, we choose silhou-
ette features that are easy to compute and locally
discriminative.
3. In the target selection stage, we choose an appro-
priate target set over which the probability density
function is evaluated.
4. In the matching stage, we estimate f(•|P
i
) at the
designated targets t
n
, using KDE technique cou-
pled with the fast Gauss Transform (FGT) (Yang
et al., 2003).
267
Tang Q. and Yang X. (2013).
3D Model Retrieval using Density-based Silhouette Descriptor.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 267-270
DOI: 10.5220/0004201602670270
Copyright
c
 SciTePress

Figure 1: The design process of the density-based silhouette.
2.1 Silhouette Extraction
In (Vranic, 2004), the author gives details about the
silhouette extraction. The projection of a 3D model is
formed through the union of projections of all trian-
gles in the mesh-model.
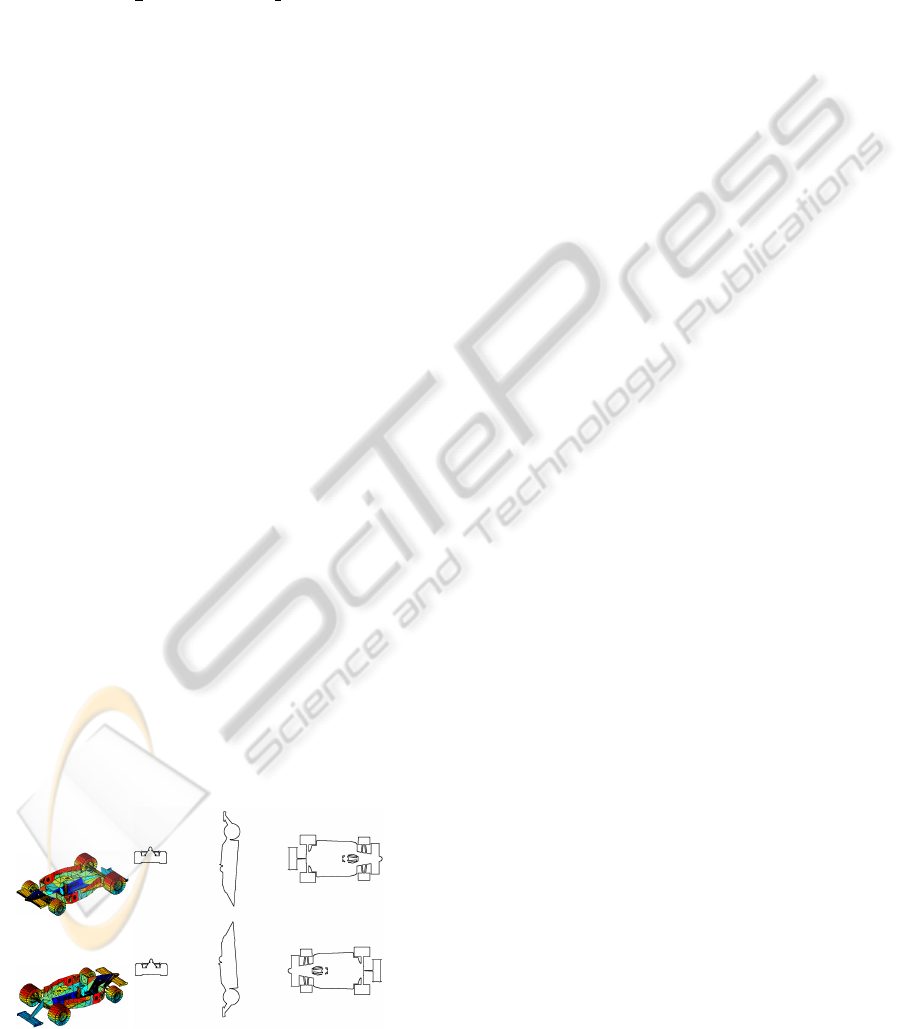
We use ”centaur0” from TOSCA (Bronstein et al.,
2006) to demonstrate DBS’s insensitivity towards
mesh resolution, see Figure 2:
Figure 2: DBS’s insensitivity towards low mesh resolution.
The model on the first row has 31532 faces and
15768 vertices, but the model on the second row only
has 1996 faces and 1000 vertices. However, their 2D
silhouettes change very little.
2.2 Local Silhouette Features
1. Zero-order Features
We use the radial distance R and the unit radial
direction
~
R as zero-order features to describe the
basic information of a silhouette. The two features
may not be effective all by themselves, but they
can be very useful in computing other features.
2. First-order Features
The unit tangent direction
~
T and the distance D
T
standing for the distance between the tangent di-
rection and the origin are considered as the first-
order features.
3. Second-order Features
The differential d
~
T of the tangent field, denoted as
~
SI and its distance, D
SI
, from the origin are con-
sidered as the second-order features.
We can construct a feature (R,
~
R,D
T
,
~
T, D
SI
,
~
SI) to
give a thorough characterization of the model’s 2D
silhouettes. However, the dimension of this feature
vector is too high, which brings in problems such as
pdf estimation accuracy, high computation time and
huge storage size. Thus, we adopt the strategy in
(Akgul et al., 2009) using multivariate pdf-based de-
scriptor with manageable dimension:
• R-descriptor, f
R|O
, represent the probability de-
scription of (R,
~
R).
• T-descriptor, f
T|O
, represent the probability de-
scription of (T,
~
T).
• SI-descriptor, f
SI|O
, represent the probability de-
scription of (SI,
~
SI).
Density-based silhouette descriptor is a combination
of the three descriptors,
DBS = a
1
∗ f
R|O
+a
2
∗ f
T|O
+a
3
∗ f
SI|O
,a
1
+a
2
+a
3
= 1
(2)
2.3 Target Selection
For scalar features, we use R as an exam-
ple. For a database containing M mod-
els, we find R
min
m
i
(m = 1, ..., M) for each
model’s projection P
m
i
and construct a vector
R
min
= (R
min
1
1
,R
min
1
2
,R
min
1
3
,...,R
min
M
1
,R
min
M
2
,R
min
M
3
).
R
lower
=
min(R
min
)+median(R
min
)
2
and R
upper
can be
obtained in the same way. Note that too small or
too large values can be eliminated. The interval
I
R
= R
upper
− R
lower
. We choose the target points of
R by partitioning the interval into N
I
R
equally spaced
subintervals and by taking the middle points.
For directional vector
~
R,
~
T and
~
S, the correspond-
ing target points should lie on the unit circle. In
the every quadrant, we partition the unit circle into
N
C
subintervals uniformly and take the middle point
of every arc. This leads a uniform partitioning of
the circle and guarantees invariance to a certain class
of 3D transformation in the matching stage. Conse-
quently, the total number of the target points should
be N = 4∗ N
I
∗ N
C
.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
268

2.4 Kernel Density Estimation
We prefer the nonparametric KDE methodology with
a Gaussian kernel, as it is flexible and computation-
ally efficient, to describe the probability density func-
tions. For a random feature S,
f
S
(t
n
|P
i
) = ((2π)
m
2
|H|)
−1
K
i
∑
k=1
w
k
e
−
1
2
(t−s
i
k
)
T
H
−2
(t−s
i
k
)
(3)
where n = 1,...,N, i = 1,2, 3
Source set

s
i
k
∈ R
S

K
i
k=1
are feature values com-
puted on the 2D silhouettes. K
i
is the total points of
the silhouettes extracted from projection P
i
.
Target set {t
n
∈ R
S
}
N
n=1
are the pdf evaluation
points.
Bandwidth H models the degree of uncertainty
about the observation and controls the smoothing be-
havior of the KDE. Appropriate bandwidth is essen-
tial for applications using KDE scheme. Computation
of the bandwidth can be seen in (Akgul et al., 2009).
2.5 Invariance of DBS
The ”continuous PCA” (Vranic, 2004) is one of uni-
versal tools for pose normalization. However, the
method does not align all models in an ideal way. As
there are 3! = 6 possible coordinate axis relabeling
and 2
3
= 8 possible polarity assignments, the admissi-
ble transformation is 6∗ 8 = 48. Each transformation
corresponds to one shape descriptor, but DBS can de-
duce the other 47 descriptors from any descriptor. We
use R-descriptor as an example.
P
1
represents the x-projection, P
2
represents the y-
projection, and P
3
represents the z-projection. When
we change x axis with y axis, the new R-descriptor is
f
′
R|O
= [ f
R
(t
1
|P
2
),... , f
R
(t
N
|P
2
), f
R
(t
1
|P
1
),... ,
f
R
(t
N
|P
1
), f
R
(t
1
|P
3
),... , f
R
(t
N
|P
3
)] (4)
When we change the polarity of x axis,the new
projections can be seen in Figure 3.
Figure 3: The effect of the change of x axis polarity on the
model’s 2D silhouettes.
As the target set is concentric circles which is
symmetric with respect to x axis and y axis, the new
R-descriptor can be obtained simply by permuting the
component of vector f
R|O
(Akgul et al., 2009), The
other descriptors can be obtained in the same way.
3 EXPERIMENTAL RESULTS
3.1 Databases and Evaluation Tools
We test the retrieval potential of DBS on two 3D
databases selected from different domains.
Princeton Shape Benchmark (PSB) (Shilane et al.,
2004) consists of a training set (907 models in 90
classes) and a test set (907 models in 92 classes). In
general, PSB meshes have low resolution and they
are non-regular, non-smooth, and contain degenera-
cies such as non-manifold, non-connectedtriangles of
varying size and shape.
GWSB2010 (Vanamali et al., 2010) contains 3168
models in 43 classes. The reason to choose this
benchmark as testing environment is that it has very
large number of 3D models, which greatly challenges
the 3D shape retrieval research community.
In order to make a thorough evaluation of a
3D shape retrieval algorithm, we employ a num-
ber of common evaluation measures (Shilane et al.,
2004) used in the retrieval community: Precision-
Recall curve, Nearest Neighbor (NN), First-tier (FT),
Second-tier (ST), E-measure (E), Discounted Cumu-
lative Gain (DCG) and Normalized DCG (NDCG).
3.2 Selection of Coefficients of DBS
As there are three coefficients in DBS, we fix one co-
efficient and observe the changes of the other coeffi-
cients on the retrieval result of DBS.
DBS = a
1
∗ f
R|O
+a
2
∗ f
T|O
+a
3
∗ f
SI|O
,a
1
+a
2
+a
3
= 1
(5)
From Table 1 we see that DBS = 0.25 ∗ f
R|O
+
0.45 ∗ f
T|O
+ 0.35∗ f
SI|O
performs the best. The rea-
son for SI-descriptor playing a less important role in
DBS is that the computation of SI-feature is not as
accurate as the computation of T-feature. This is also
the reason that we do not use higher-order features.
3.3 Retrieval Comparisons
and Performance Analysis
In this section, we first compare the retrieval perfor-
mance of DBS against some other representative 3D
3DModelRetrievalusingDensity-basedSilhouetteDescriptor
269

Table 1: DCG (Percent) Performance of DBS with different
coefficients on PSB test.
a2/a3 0.0 0.1 0.2 0.3 0.4 0.5
0.0 61.2 62.7 64.0 65.1 65.5 65.7
0.1 62.5 63.9 65.2 66.1 66.6 66.6
0.2 63.6 64.9 66.1 66.9 67.3 67.1
0.3 64.4 65.7 66.7 67.5 67.6 67.4
0.4 65.1 66.2 67.1 67.7 67.6 67.1
0.5 65.5 66.5 67.2 67.4 67.3 66.4
0.6 65.6 66.6 67.0 67.1 66.4
0.7 65.6 66.2 66.6 66.3
0.8 65.3 65.7 65.9
0.9 64.8 64.9
1.0 63.9
Table 2: Retrieval statistics (Percent) of state-of-art 3D
shape descriptors on PSB test.
Descriptor NN DCG NDCG
DBS 70.5 67.8 8.7
CRSP 67.9 66.8 7.1
DSR 66.5 66.5 6.6
DBF 68.6 65.9 5.7
SWD 46.9 65.4 4.9
LFD 65.7 64.3 3.1
DBI 60.9 61.4 -1.6
REXT 60.2 60.1 -3.7
SIL 55.7 59.7 -4.3
RISH 55.6 58.4 -6.4
3DHT 58.8 57.7 -7.5
SHIST 54.6 54.5 -12.6
model retrieval algorithms on PSB. The other statis-
tics given in Table 2 are taken from the study in
(Akgul et al., 2009).
From Table 2 we see that though PSB is one of
the most challenging databases, DBS is among the top
cluster. The reason is that low resolution and degen-
eracies can be avoided in computing DBS and these
are main characters of models in PSB.
The other statistics in Table 3 are taken from the
study in (Vanamali et al., 2010). From Table 4 we see
that DBS can also perform well on a large database.
Compared to SIL, DBS has a better performance.
4 CONCLUSIONS
In this work, we have introduced a new 3D shape
descriptor, Density-Based Silhouette descriptor. The
new descriptor inherits advantages from both DBF
and SIL and shows high retrieval accuracy on several
3D databases with varying mesh resolution, semantic
content and classification granularity. On PSB, one of
Table 3: Retrieval statistics (Percent) of state-of-art 3D
shape descriptors on GWSB2010.
Descriptor NN FT ST E DCG
DSR472 87.1 49.8 63.9 35.6 83.1
LFD 86.4 48.0 61.3 33.6 81.6
DBS 80.9 41.5 56.0 30.1 78.2
SIL300 80.7 41.2 54.8 30.0 78.0
DSR438 80.9 40.7 53.2 30.6 77.0
RSH136 78.3 38.5 50.8 27.5 75.8
the most challenging database, its DCG is nearly two
percent higher than DBF’s. On GWSB2010 which
has more than 3000 models, DBS also has a high re-
trieval accuracy. The retrieval experiments on two
databases show that DBS can be adapted to a broad
and heterogeneous set of shape categories.
REFERENCES
Akgul, C., Sankur, B., Yemez, Y., and Schmitt, F. (2009). 3d
model retrieval using probability density-based shape
descriptors. IEEE Trans on Pattern Analysis and Ma-
chine Intelligence, 31(6):1117–1133.
Bronstein, A., Bronstein, M., and Kimmel, R. (2006). Effi-
cient computation of isometry-invariant distances be-
tween surfaces. In SIAM J. Scientific Computing, vol-
ume 28, pages 1812–1836.
Li, B., Godil, A., Aono, M., and Bai, X. (2012). Shrec’12
track: Generic 3d shape retrieval. Eurographics Work-
shop on 3D Object Retrieval.
Marini, S., Paraboschi, L., and Biasotti, S. (2007). Shape
retrieval contest 2007: Partial matching track. In Proc.
SHREC in Conjunction with Proc. Intl Conf. Shape
Modeling and Applications, pages 13–16.
Min, P., Kazhdan, M., and Funkhouser, T. (2004). A com-
parison of text and shape matching for retrieval of on-
line 3d models. In Proc. European conference on dig-
ital libraries, pages 209–220.
Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T.
(2004). The princeton shape benchmark. In Proc.
Shape Modeling Int’l, pages 167–178.
Tangelde, J. and Veltkamp, R. (2008). A survey of content
based 3d shape retrieval methods. Multimedia Tools
and Applications.
Vanamali, T., Godil, A., Dutagaci, H., Furuya, T., Lian, Z.,
and Ohbuchi, R. (2010). Shrec’10 track: Generic 3d
warehouse. Eurographics Workshop on 3D Object Re-
trieval.
Vranic, D. (2004). 3D Model Retrieval. PhD dissertation,
Univ. of Leipzig.
Yang, C., Duraiswami, R., Gumerov, N., and Davis, L.
(2003). Improved fast gauss transform and efficient
kernel density estimation. In Proc. Int’l Conf. Com-
puter Vision, volume 1, page 464.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
270