
The Distribution of Short Word Match Counts
between Markovian Sequences
Conrad J. Burden
1
, Paul Leopardi
1
and Sylvain For
ˆ
et
2
1
Mathematical Sciences Institute, Australian National University, Canberra, ACT 0200, Australia
2
Research School of Biology, Australian National University, Canberra, ACT 0200, Australia
Keywords:
Word Matches, Biological Sequence Comparison.
Abstract:
The D
2
statistic, which counts the number of word matches between two given sequences, has long been
proposed as a measure of similarity for biological sequences. Much of the mathematically rigorous work
carried out to date on the properties of the D
2
statistic has been restricted to the case of ‘Bernoulli’ sequences
composed of identically and independently distributed letters. Here the properties of the distribution of this
statistic for the biologically more realistic case of Markovian sequences is studied. The approach is novel
in that Markovian dependency is defined for sequences with periodic boundary conditions, and this enables
exact analytic formulae for the mean and variance to be derived. The formulae are confirmed using numerical
simulations, and asymptotic approximations to the full distribution are tested.
1 INTRODUCTION
The D
2
statistic, defined as the number of short word
matches of pre-specified length k between two se-
quences of letters from a finite alphabet A . This statis-
tic (Lippert et al., 2002), and its many variants (Vinga
and Almeida, 2003; Reinert et al., 2009; G
¨
oke et al.,
2012; Jing et al., 2011) have been proposed as a
measures of similarity between biological sequences
in cases where the more commonly used alignment
methods may not be appropriate. The distributional
properties of the D
2
statistic under the null hypothesis
of sequences composed of independently and identi-
cally distributed (i.i.d.) letters have been studied ex-
tensively (Lippert et al., 2002; For
ˆ
et et al., 2006; Kan-
torovitz et al., 2006; For
ˆ
et et al., 2009b; For
ˆ
et et al.,
2009a; Burden et al., 2012).
Analysis of the k-mer spectra of the genomes of
several species provides strong evidence that genomic
sequences are more approptriately modelled as hav-
ing a Markovian dependence (Chor et al., 2009). In
the current work existing exact analytic results results
for the mean, variance and an empirical distribution
of D
2
for i.i.d. sequences is extended to the case of
Markovian sequences.
A previous study of this problem, with some ap-
proximations, has been carried out by Kantorovitz et
al. (Kantorovitz et al., 2007) in the process of devel-
oping a method for detecting regulatory modules in
genomic sequences. The current study differs in that
we consider sequences with periodic boundary condi-
tions (PBCs), for which we introduce a new definition
of Markovian sequences. The restriction to periodic
sequences simplifies calculations of the mean and
variance, enabling an exact analytic formula for the
variance for first order Markovian sequences which is
rapidly computable to double precision accuracy for
arbitrary sequence lengths. In biological aplications
of the analogous results for i.i.d. sequences (For
ˆ
et
et al., 2009a; Burden et al., 2012) we have found gen-
erally that the PBCs are not an impediment, as they
can simply be imposed on the sequences prior to cal-
culating D
2
without without seriously affecting its ef-
ficacy as a measure of sequence similarity.
2 DEFINITIONS
Consider a sequence x = x
1
,x
2
... of letters from an
alphabet A of size d. We say that x has periodic
boundary conditions (PBCs) and is of length m if
x
i+m
= x
i
for all i = 1,2,.. ..
A sequence X = X
1
,X
2
... of random letters has an
ω-th order Markovian dependence if
Prob ((X
i+ω
= b|(X
i
,... ,X
i+ω−1
= (a
1
,... ,a
ω
))
= M(a
1
,... ,a
ω
;b), (1)
25
J. Burden C., Leopardi P. and Forêt S..
The Distribution of Short Word Match Counts between Markovian Sequences.
DOI: 10.5220/0004203700250033
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 25-33
ISBN: 978-989-8565-35-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

for a specified d
ω
× d matrix M satisfying
0 ≤ M(a
1
,... ,a
ω
;b) ≤ 1;
∑
b∈A
M(a
1
,... ,a
ω
;b) = 1,
(2)
for all a
1
,... ,a
ω
,b ∈ A. As a shorthand notation, we
will write a string of length ω with an arrow above:
~x = (x
1
,... x
ω
), (3)
and write any substring of X of length ω in a similar
fashion, labelled by the index of the first element:
~
X
i
= (X
i
,... X
i+ω−1
), (4)
Thus Eq.(1) is written more compactly as
Prob (X
i+ω
= b|
~
X
i
=~a) = M(~a;b). (5)
Following the notation of ref. (Reinert et al., 2005),
define a d
ω
× d
ω
square matrix M as
M(~a,
~
b) =
(
M(~a; b
ω
) if (a
2
,...,a
ω
) = (b
1
,...b
ω−1
),
0 otherwise.
(6)
Then the Markovian dependency can be written as
a first order Markovian dependency as
Prob (
~
X
i+1
=
~
b|
~
X
i
=~a) = M(~a,
~
b). (7)
2.1 Markovian Sequences with PBCs
Given an order ω Markovian matrix M, we first at-
tempt to define a periodic random sequence X =
X
1
,X
2
..., X
n
of length n via the following algorithm:
Algorithm 1.
Step 0: Choose a probability distribution on the set
of strings of length ω:
Prob (
~
X
1
= ~x) = π(~x), where 0 ≤ π(~x) ≤ 1 and
∑
~x∈A
ω
π(~x) = 1.
Step 1: Generate
~
X
1
= X
1
,... X
ω
from this distribu-
tion.
Step 2: Generate X
ω+1
,... ,X
ω+n
using Eq. (7).
Step 3: If
~
X
n+1
=
~
X
1
, accept the sequence X =
X
1
,X
2
..., X
n
, otherwise repeat from Step 1 until
an accepted sequence is obtained.
Clearly this algorithm entails that
Prob (X = x) = (8)
π(~x
1
)M(~x
1
,~x
2
),M(~x
2
,~x
3
)... M(~x
n
,~x
1
)
∑
~u
1
,...,~u
n
∈A
ω
π(~u
1
)M(~u
1
,~u
2
),M(~u
2
,~u
3
)... M(~u
n
,~u
1
)
.
The idea behind PBCs is that there should be no priv-
ileged position along the sequence from which to be-
gin numbering. Thus we further impose a condition
that the sequence should have no privileged starting
point, that is, for each i = 1,... ,n,
Prob (X = x
i+1
x
i+2
...x
n
x
1
...x
i
) = Prob (X = x).
(9)
Eqs. (8) and (9) imply that π(~x
i+1
) = π(~x
1
) for each i
and for very sequence x ∈ A
n
, which can only happen
if
π(~x) =
1
d
ω
∀~x ∈ A
ω
. (10)
This leads to the following definition:
Definition 1. Given a Markovian matrix M of or-
der ω, a random Markovian sequence with PBCs of
length n is one generated by Algorithm 1 with the ini-
tial distribution π in Step 0 equal to the uniform dis-
tribution Eq. (10).
It follows from Eq. (8) that for a random Marko-
vian sequence X of length n, the probability of the
configuration x = (x
1
..., x
m
) occuring is
Prob (X = x) =
M(~x
1
,~x
2
)M(~x
2
,~x
3
)... M(~x
m
,~x
1
)
tr (M
m
)
.
(11)
3 THE D
2
STATISTIC
Definition 2. Given random Markov sequences X and
Y with PBCs of length m and n respectively, the D
2
statistic is defined as the number of k-word matches,
including overlaps, between X and Y:
D
2
=
m
∑
i=1
n
∑
j=1
I
i j
, (12)
where I
i j
is the word match indicator random variable
for words length k positioned at site i in sequence X
and site j in sequence Y:
I
i j
=
(
1 if (X
i
,... ,X
i+k−1
) = (Y
j
,... ,Y
j+k−1
),
0 otherwise.
(13)
3.1 D
2
Mean for Arbitrary ω
Define the Hadamard product A ◦ B of two matrices
A and B as the matrix whose (α,β)-th element is
(A ◦ B)
αβ
= A
αβ
B
αβ
. (14)
The mean of D
2
is
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
26

E(D
2
) =
mn
tr (M
m
)tr (M
n
)
×
tr [(M
m−k+ω
◦ M
n−k+ω
)(M ◦ M)
k−ω
]
if k ≥ ω,
mn
tr (M
m
)tr (M
n
)
×
∑
u,v∈A
k−ω
∑
w∈A
k
M
m
((wu),(wu))M
n
((wv),(wv))
if k < ω,
(15)
where (wu) means the ω-tuple (w
1
...w
k
u
1
...u
ω−k
)
and similarly for (wv).
Proof. We have that
E(D
2
) =
m
∑
i=1
n
∑
j=1
E(I
i j
) =
m
∑
i=1
n
∑
j=1
Prob (I
i j
= 1), (16)
where
Prob (I
i j
= 1) =
∑
w∈A
k
Prob (X
i
...X
i+k−1
= w)×
Prob (Y
j
...Y
j+k−1
= w). (17)
To calculate Prob (X
i
...X
i+k−1
= w) we must con-
sider separately the cases k ≥ ω and k < ω
Consider first the case where k ≥ ω. The required
probability is calculated by summing Eq.(11) over all
sequences x such that (x
i
...x
i+k−1
) = w. The defini-
tion of the matrix M, Eq.(6), ensures that it is suffi-
cient to restrict only those ω-tuples ~x
i
located within
the word w, since contributions to the sum from any
partially overlapping ω-tuples will be zero unless the
overlap letters match those of w (see Fig. 1(a)). Thus
Prob (X
i
...X
i+k−1
= w) =
M
m−k+ω
(~w
k−ω+1
,~w
1
)M(~w
1
,~w
2
)...M(~w
k−ω
,~w
k−ω+1
)
tr (M
m
)
(18)
where the ω-tuples~x
1
,... ,~x
i−1
,~x
i+k−ω+1
,... ,~x
m
have
been summed over. Similarly we have
Prob (Y
j
...Y
j+k−1
= w) =
M
n−k+ω
(~w
k−ω+1
,~w
1
)M(~w
1
,~w
2
)...M(~w
k−ω
,~w
k−ω+1
)
tr (M
n
)
.
(19)
The definition of the matrix M ensures that
the sum over the k-word w in Eq. (17) is equiv-
alent to a sum over a set of independent ω-tuples
w
1
w
2
w
k–ω+1
...
w
x
i+k-ω+1
x
i+k-ω+2
...
x
i-2
x
i-1
...
X:
k
ω
(a)
w
x
i+1
x
i+2
...
x
i-2
x
i-1
X:
k
(b)
w u
ω
...
Figure 1: Covering of the sequence X with ω-tuples for the
calculation of Prob (X
i
...X
i+k−1
= w) (a) in the case where
k ≥ ω, and (b) in the case where k < ω.
~w
1
,... ,~w
k−ω+1
. Thus substituting Eqs. (18) and (19)
into Eq. (17) gives
Prob (I
i j
= 1) =
tr [(M
m−k+ω
◦ M
n−k+ω
)(M ◦ M)
k−ω
]
tr (M
m
)tr (M
n
)
(20)
Eq. (16) then gives the required result for the case k ≥
ω.
For the case k < ω, the Prob (X
i
...X
i+k−1
= w)
is again calculated by summing Eq.(11) over all se-
quences x such that (x
i
...x
i+k−1
) = w. In this case
it is sufficient to restrict any one of ω-tuples overlap-
ping w to equal w on the overlap, and the structure of
M will ensure that only terms in which the other over-
lapping ω-tuples match w will contribute to the sum.
Accordingly set ~x
i
= (w
1
...w
k
u
1
...u
ω−k
), where the
u
1
...u
ω−k
are not fixed (see Fig. 1(b)). Then
Prob (X
i
...X
i+k−1
= w) =
1
tr (M
m
)
∑
u∈A
ω−k
M
m
((wu),(wu)), (21)
and similarly
Prob (Y
j
...Y
j+k−1
= w) =
1
tr (M
n
)
∑
v∈A
ω−k
M
n
((wv),(wv)). (22)
Substituting these two probabilities into Eqs.(17) and
(16) gives the required result.
TheDistributionofShortWordMatchCountsbetweenMarkovianSequences
27

3.2 D
2
Variance for ω = 1
The exact variance of D
2
for Markovian sequences
with PBCs requires an extensive calculation. The
case ω > 1 remains intractable, essentially for the
same reason that it was necessary to treat the k < ω
case separately for the above derivation of the mean;
namely that probabilities must be calculated for se-
quence configurations that cannot be covered with ω-
tuples conveniently lying within certain specified seg-
ments. Nevertheless, the variance can be calculated
for the ω = 1 case. Here we give a summary of the
result, which is valid for m,n ≥ 2k. Full technical de-
tails of the derivation will be published elsewhere.
We have
Var (D
2
) = E(D
2
2
) − E(D
2
)
2
. (23)
The second term can be calculated from Eq.(15). The
first term is a sum of contributions obtained from
Eq.(12) by partitioning a sum over words beginning
at positions i and i
0
in sequence X and beginning at j
and j
0
in sequence Y,
E(D
2
2
) =
m
∑
i,i
0
=1
n
∑
j, j
0
=1
E(I
i j
I
i
0
j
0
)
=
m
∑
i,i
0
=1
n
∑
j, j
0
=1
Prob (I
i j
= 1, I
i
0
j
0
= 1)
= V
0
+V
1
+V
2
+V
3
+V
4
. (24)
The partitioning reflects the degree of overlap be-
tween words in each of the two sequences, and is il-
lustrated in Fig. 2. We assume m, n ≥ 2k, which will
almost certainly be the case in any biological applica-
tion.
We will write a Hadamard product of q factors,
M ◦ ... ◦ M, using the shorthand notation M
◦q
. With
this notation, the contributions to the variance are:
V
0
=
mn
tr (M
m
)tr (M
n
)
×
m−2k
∑
r=0
n−2k
∑
s=0
tr
h
(M
r+1
◦ M
s+1
)(M ◦ M)
k−1
×
(M
m−2k−r+1
◦ M
n−2k−s+1
)(M ◦ M)
k−1
i
,
(25)
V
1
=
mn
tr (M
m
)tr (M
n
)
×
(
n−2k
∑
s=0
h
tr {[(M ◦ M ◦ M)
k−1
◦ (M
s+1
)
T
]×
(M
m−k+1
◦ M
n−2k−s+1
)}
+2
k−1
∑
r=1
tr {(M ◦ M)
r
×
[(M ◦ M ◦ M)
k−r−1
◦ (M
s+1
)
T
] ×
(M ◦ M)
r
(M
m−k−r+1
◦ M
n−2k−s+1
)
oi
+ the same with m and n interchanged.
)
,
(26)
V
2
=
mn
tr (M
m
)tr (M
n
)
×
(
tr [(M
m−k+1
◦ M
n−k+1
)(M ◦ M)
k−1
]
+2
k−1
∑
t=1
tr [(M
m−k−t+1
◦ M
n−k−t+1
) ×
(M ◦ M)
k+t−1
]
)
,
(27)
V
3
=
2mn
tr (M
m
)tr (M
n
)
×
k−1
∑
t=1
t−1
∑
s=0
tr
(M ◦ M)
s
Q(M ◦ M)
s
×
(M
m−k−t+1
◦ M
n−k−s+1
+
M
n−k−t+1
◦ M
m−k−s+1
)
,
(28)
where
Q =
(M
◦(2ν+3)
)
ρ−1
◦ [(M
◦(2ν+1)
)
t−s−ρ+1
]
T
if ρ > 0,
(M
◦(2ν+1)
)
t−s−1
◦ (M
◦(2ν−1)
)
T
if ρ = 0,
(29)
and
ν =
k − s
t − s
, ρ = (k − s) mod (t − s). (30)
Finally,
V
4
=
2mn
tr (M
m
)tr (M
n
)
k−1
∑
r,t=1
tr U, (31)
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
28

–k + 1, … , –1, 0, 1, … , k – 1
t
–k + 1
0
k – 1
s
V
4
V
4
V
3
V
3
V
3
V
3
... ...
V
2
(i, j)
m
n
2k − 1
2k − 1
V
1
V
1
V
1
V
1
V
0
V
0
V
0
V
0
i’
j’
Figure 2: Contributions to Var (D
2
) via the sum in Eq. (24). The left-hand diagram shows the (i
0
, j
0
)-plane for a fixed value of
(i, j), shown as the black square. The right-hand diagram is an expanded view of the ‘accordion’ region −k + 1 ≤ s,t ≤ k − 1,
where t = i
0
− i and s = j
0
− j up to PBCs.
where
U =
n
(M
◦(2ν+1)
)
t−1
◦ (M
m−k−t+1
)
T
o
M
◦2ν
×
n
(M
◦(2ν+1)
)
r−1
◦ (M
n−k−r+1
)
T
o
M
◦2ν
if ζ = 0,
n
(M
◦(2ν+1)
)
r−ζ+1
◦ M
m−k−t+1
o
×
(M
◦(2ν+2)
)
ζ−1
×
n
(M
◦(2ν+1)
)
t−ζ+1
◦ M
n−k−r+1
o
×
(M
◦(2ν+2)
)
ζ−1
if 0 < ζ ≤ r,t,
n
(M
◦(2ν+3)
)
ζ−r−1
◦ (M
m−k−t+1
)
T
o
×
(M
◦(2ν+2)
)
r
n
(M
◦(2ν+1)
)
t−ζ+1
◦ M
n−k−r+1
o
×(M
◦(2ν+2)
)
r
if r < ζ ≤ t,
{as above with m and n interchanged
and r and t interchanged}
if t < ζ ≤ r,
n
(M
◦(2ν+3)
)
ζ−r−1
◦ (M
m−k−t+1
)
T
o
×
(M
◦(2ν+2)
)
t+r−ζ+1
×
n
(M
◦(2ν+3)
)
ζ−t−1
◦ (M
n−k−r+1
)
T
o
×
(M
◦(2ν+2)
)
t+r−ζ+1
if r,t < ζ,
and
ν =
k
r +t
, ζ = k mod (r +t). (32)
4 NUMERICAL SIMULATIONS
For short sequences and small alphabets the distribu-
tion of the D
2
statistic can be computed by enumer-
ating all possible sequences. We have confirmed the
accuracy of the formulae for the mean and variance
given in Section 3 to 11 significant figures by generat-
ing the complete distribution of D
2
using double pre-
cision arithmetic for sequences up to length m = n = 9
for k = 3, d = 2 and up to length m = n = 7 for k = 2,
D = 3. The Markov matrices M are generated ran-
domly by choosing each element from a uniform dis-
tribution on the interval [0, 1] and then normalising
each row sum to 1. Two examples of the exact D
2
distribution are shown in Figure 3. Note that the in-
troduction of random Markov matrices is to enable an
efficient check of the above formulae for a range of
M, and is not intended to have any biological mean-
ing. Maximum likelihood estimates of Markov ma-
trices from various genomes have been published, for
instance, by Chor et al. (Chor et al., 2009), which can
be used in biological applications.
For longer sequences of realistic biological length,
the distribution of D
2
can be estimated from a Monte
Carlo ensemble of random sequences generated from
the algorithm described in Section 2.1. Examples of
cumulative distribution functions for d = 4, k = 4 es-
timated from ensembles of 10,000 pairs of indepen-
dently generated random sequences of length m = n =
100 and 400 are shown in Figures 4 and 5 respec-
tively. The Markov matrix is again generated ran-
domly, and it is interesting to note that the mean of
the distribution can vary considerably with M. We
TheDistributionofShortWordMatchCountsbetweenMarkovianSequences
29
0 10 20 30 40 50
0.00 0.05 0.10 0.15
nA = 7 nB = 7 d = 3 k = 2
x
Prob(D
2
= x)
M =
0.338 0.343 0.319
0.349 0.427 0.223
0.258 0.312 0.43
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
x
Prob(D
2
≤ x)
0 20 40 60 80
0.00 0.02 0.04 0.06
nA = 9 nB = 9 d = 2 k = 3
x
Prob(D
2
= x)
M =
0.758 0.242
0.58 0.42
0 20 40 60 80
0.0 0.2 0.4 0.6 0.8 1.0
x
Prob(D
2
≤ x)
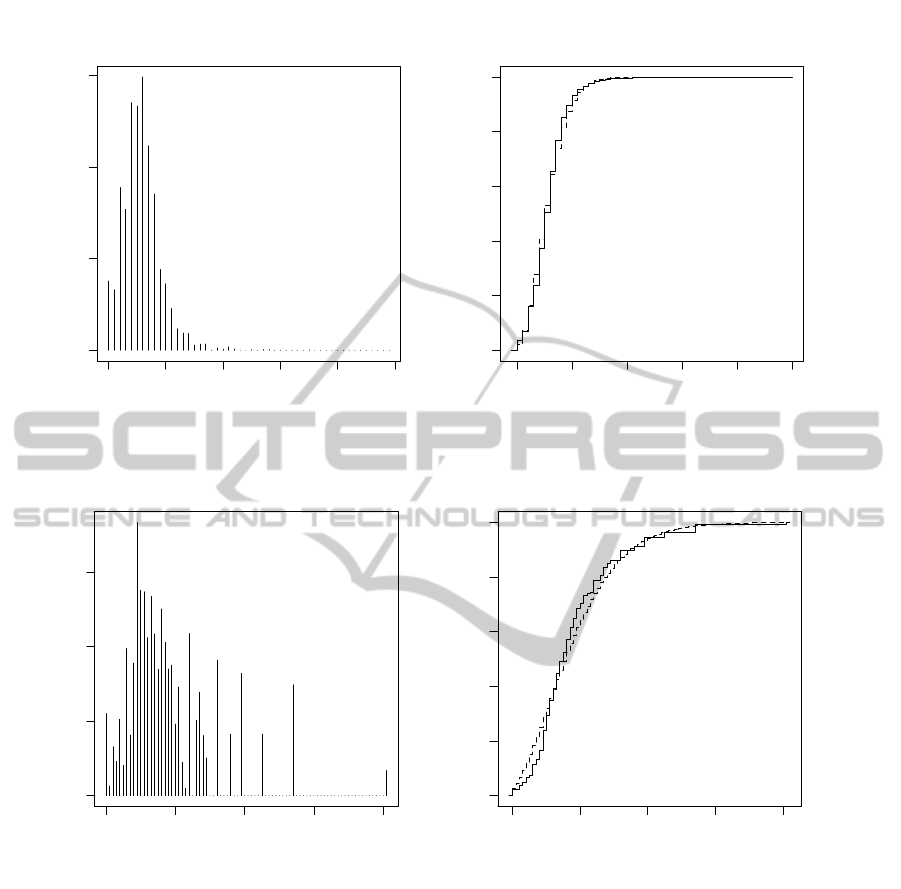
Figure 3: The exact distiribution of the D
2
statistic for short sequences of length m, n and words of length k from an alphabet
of size d. The Markov matrix M has been generated randomly in each case. Also shown (dashed curve) is the cumula-
tive distribution of the P
´
olya-Aeppli distribution with mean and variance set to the theoretical values using the formulae of
Section 3.
have made a number of simulations, and find that in
roughly the expected proportion of times the mean
and variance calculated from the formulae of Sec-
tion 3 lie within the 95% confidence intervals com-
puted from the ensemble.
For the case of sequences composed of i.i.d. letters
certain rigorous results are known for the asymptotic
distribution of D
2
as the sequence lengths m,n → ∞.
For m = n, it has been shown that the limiting dis-
tribution is normal in the regime k < 1/2 log
b
n +
const. (Burden et al., 2008) and P
´
olya-Aeppli in the
regime k > 2 log
b
n + const. (Lippert et al., 2002).
Here b = 1/
∑
a∈A
p
2
a
where p
a
is the probability of
occurrence of letter a. A P
´
olya-Aeppli random vari-
able is the sum of a Poisson number of geometric ran-
dom variables, and is therefore an example of a com-
pound Poisson random variable. It often arises in the
study of random word counts as a Poisson number of
clumps of overlapping words, each clump containing
a geometric number of k-words (Reinert et al., 2005).
Although the asymptotic results for D
2
are not proved
for Markovian sequences, it is a reasonable experi-
ment to compare our numerical simulations with these
distributions as they may potentially provide an accu-
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
30
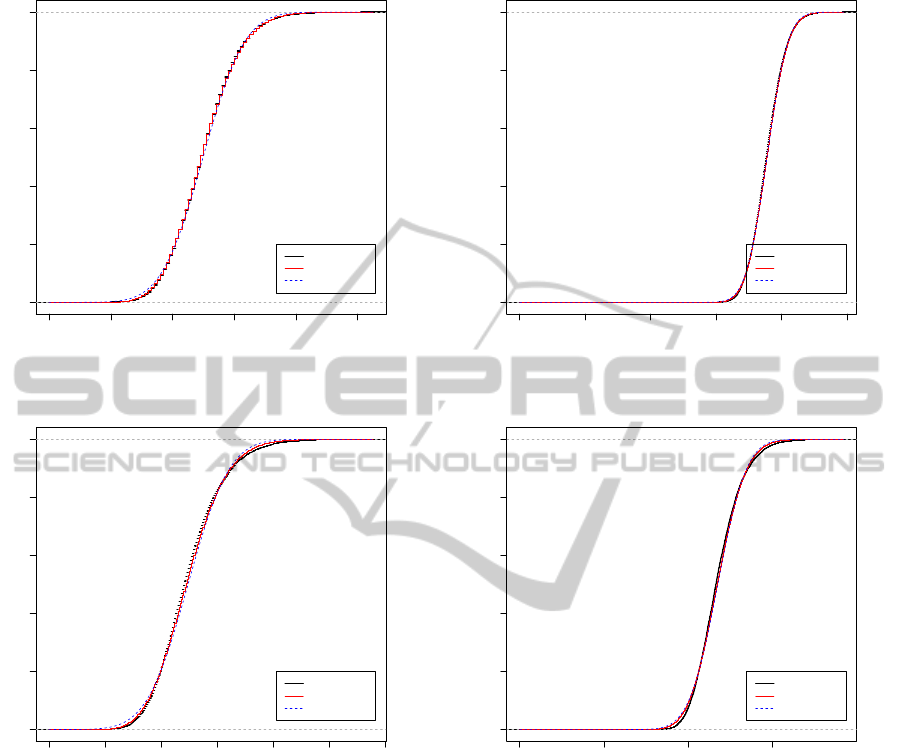
0 20 40 60 80 100
0.0 0.2 0.4 0.6 0.8 1.0
n = 100 k = 4
M =
0.344 0.087 0.283 0.286
0.245 0.226 0.254 0.275
0.16 0.181 0.309 0.35
0.187 0.34 0.267 0.207
D2
Polya−Aeppli
Normal
0 50 100 150 200 250 300
0.0 0.2 0.4 0.6 0.8 1.0
n = 100 k = 4
M =
0.432 0.315 0.074 0.179
0.193 0.011 0.27 0.526
0.317 0.208 0.196 0.279
0.542 0.339 0.117 0.002
D2
Polya−Aeppli
Normal
Figure 4: Two examples of empirical cumulative distri-
bution of the D
2
statistic estimated from 10,000 indepen-
dently generated random sequences of length m = n = 100
for words of length k = 4 and an alphabet of size d = 4.
The Markov matrix M has been generated randomly in each
case. Also shown are the cumulative distribution of the nor-
mal and P
´
olya-Aeppli distributions with mean and variance
set to the theoretical values using the formulae of Section 3.
rate estimate of p-values in biological applications.
One would not expect the asymptotic distributions
to be an accurate fit for the short sequences considered
in Figure 3. Nevertheless we have included the P
´
olya-
Aeppli distribution function and find it to be surpris-
ingly close for the d = 3 case. Disagreement arises in
the tail of the distribution because, for combinatoric
reasons, certain values of D
2
within the range 0 to mn
do not occur, whereas the P
´
olya-Aeppli has support
over the whole range (and also out to ∞, albeit with
very low probability).
0 200 400 600 800 1000
0.0 0.2 0.4 0.6 0.8 1.0
n = 400 k = 4
M =
0.305 0.27 0.171 0.254
0.338 0.308 0.136 0.218
0.152 0.199 0.298 0.351
0.188 0.273 0.253 0.286
D2
Polya−Aeppli
Normal
0 500 1000 1500
0.0 0.2 0.4 0.6 0.8 1.0
n = 400 k = 4
M =
0.281 0.382 0.256 0.082
0.201 0.42 0.104 0.275
0.316 0.18 0.27 0.233
0.065 0.435 0.211 0.289
D2
Polya−Aeppli
Normal
Figure 5: The same as Figure 4, except m = n = 400.
If one were dealing with i.i.d. sequences with a
uniform letter distribution, then the parameters m =
n = 100 or 400, k = 4 used for the simulations in Fig-
ures 4 and 5 would inhabit the region between the nor-
mal and P
´
olya-Aeppli asymptotic regimes described
above. Both asymptotic distributions are superim-
posed on the empirical distribution functions in Fig-
ures 4 and 5. We observe that the normal and P
´
olya-
Aeppli do not differ greatly from one another, though
the P
´
olya-Aeppli does appear to give a better fit, par-
ticularly in the important tail of the distribution rele-
vant to estimating p-values.
TheDistributionofShortWordMatchCountsbetweenMarkovianSequences
31

5 CONCLUSIONS
This paper introduces the concept of periodic bound-
ary conditions for Markovian sequences as an ele-
gant mathematical construct which avoids the incon-
venience of boundary effects in analytic calculations.
We have demonstrated that the mean and variance of
the D
2
word match statistic can be calculated analyt-
ically and readily computed to any desired accuracy
through formulae involving only traces of products
of matrices. Calculation of the mean and variance
is fast as powers of Hadamard products need only
be calculated once for a given Markovian model, and
only need to be calculated up to the point of conver-
gence. For biological applications such as measuring
sequence similarity or identifying regions of regula-
tory motifs, sequences lengths tend to be of at least
a few hundred letters. In these cases loss of infor-
mation about boundary effects is unlikely to be a se-
rious impediment. For instance, in previous studies
of a database of cis-regulatory modelled as a set of
i.i.d. sequences was successfully studied using the D
2
statistics simply by imposing PBCs on the sequences
prior to calculating the D
2
(For
ˆ
et et al., 2009a; Burden
et al., 2012).
The current work is a preliminary study designed
to illustrate the computational effectiveness of im-
posing periodic boundary conditions when calculat-
ing the D
2
statistic. In ongoing work we are test-
ing the agreement between the theoretical Markovian
distributions studied herein and empirical distribu-
tions from genomic DNA. In general, we find that the
empirical distribution tends to have heavier left and
right tails, suggesting the existence of a subset of k-
mers which are over- or under-represented within the
genomes studied.
Further work also needs to be done on extending
the results to more viable variants of the D
2
statistic.
It has been argued that a potential shortcoming of the
D
2
statistic is that the signal of sequence similarity
one is trying to detect maybe hidden by its variability
due to noise in each of the single sequences, and that
to overcome this problem one should instead calcu-
late a ‘centred’ version of D
2
in which word count
vectors are replaced with those centred about their
mean (Lippert et al., 2002; Reinert et al., 2009). There
also exist ‘standardised’ versions of D
2
(Liu et al.,
2011; G
¨
oke et al., 2012) designed to account for bi-
ases arising from the fact that some words are natu-
rally over-represented, and ‘weighted’ versions (Jing
et al., 2011) designed to account for higher substitu-
tion rates of chemically similar amino acids in protein
sequences. Extension of the mathematical formalisms
developed herein to these D
2
variants, as well as a
more compete study of the accuracy of approximat-
ing p-values with asymptotic distributions, will be the
subject of future work.
ACKNOWLEDGEMENTS
This work was funded in part by ARC Discovery
grants DP0987298 and DP120101422.
REFERENCES
Burden, C. J., Jing, J., and Wilson, S. R. (2012). Alignment-
free sequence comparison for biologically realistic se-
quences of moderate length. Statistical Applications
in Genetics and Molecular Biology, 11(1):Article 3.
Burden, C. J., Kantorovitz, M. R., and Wilson, S. R. (2008).
Approximate word matches between two random se-
quences. Annals of Applied Probability, 18(1):1–21.
Chor, B., Horn, D., Goldman, N., Levy, Y., and Massing-
ham, T. (2009). Genomic DNA k-mer spectra: models
and modalities. Genome Biology, 10:R108.
For
ˆ
et, S., Kantorovitz, M. R., and Burden, C. J. (2006).
Asymptotic behaviour and optimal word size for ex-
act and approximate word matches between random
sequences. BMC Bioinformatics, 7 Suppl 5:S21.
For
ˆ
et, S., Wilson, S. R., and Burden, C. J. (2009a). Charac-
terizing the D2 statistic: Word matches in biological
sequences. Stat. Appl. Genet. Mo. B., 8(1):Article 43.
For
ˆ
et, S., Wilson, S. R., and Burden, C. J. (2009b). Empir-
ical distribution of k-word matches in biological se-
quences. Pattern Recogn., 42:539–548.
G
¨
oke, J., Schulz, M., Lasserre, J., and Vingron, M. (2012).
Estimation of pairwise sequence similarity of mam-
malian enhancers with word neighbourhood counts.
Bioinformatics, 28(5):656–663.
Jing, J., Wilson, S. R., and Burden, C. J. (2011). Weighted
k-word matches: A sequence comparison tool for pro-
teins. ANZIAM J., page To appear.
Kantorovitz, M. R., Booth, H. S., Burden, C. J., and Wilson,
S. R. (2006). Asymptotic behavior of k-word matches
between two uniformly distributed sequences. J. Appl.
Probab., 44:788–805.
Kantorovitz, M. R., Robinson, G. E., and Sinha, S. (2007).
A statistical method for alignment-free comparison of
regulatory sequences. Bioinformatics, 23(13):i249–
55.
Lippert, R. A., Huang, H., and Waterman, M. S. (2002).
Distributional regimes for the number of k-word
matches between two random sequences. Proc. Natl.
Acad. Sci. USA, 99(22):13980–9.
Liu, X., Wan, L., Li, J., Reinert, G., Waterman, M. S., and
Sun, F. (2011). New powerful statistics for alignment-
free sequence comparison under a pattern transfer
model. J. Theoret. Biol., 284:106–116.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
32

Reinert, G., Chew, D., Sun, F., and Waterman, M. S. (2009).
Alignment-free sequence comparison (i): statistics
and power. J. Comput. Biol., 16(12):1615–1634.
Reinert, G., Schbath, S., and Waterman, M. (2005). Statis-
tics on words with applications to biological se-
quences. In Lothaire, M., editor, Applied Combi-
natorics on Words, chapter 6. Cambridge University
Press.
Vinga, S. and Almeida, J. (2003). Alignment-free sequence
comparison-a review. Bioinformatics, 19(4):513–23.
TheDistributionofShortWordMatchCountsbetweenMarkovianSequences
33
