
A Combinatorial Optimization Approach for the Electrical Energy
Management in a Multi-source System
Yacine Gaoua
1,2,3
, St´ephane Caux
1
and Pierre Lopez
2,3
1
LAPLACE UMR 5213 CNRS, INPT, UPS, 2 rue Camichel, F-31071 Toulouse, France
2
CNRS, LAAS, 7 avenue du colonel Roche, F-31400 Toulouse, France
3
Univ de Toulouse, LAAS, F-31400 Toulouse, France
Keywords:
Energy Management, Modeling, Combinatorial Optimization, Off-line Optimization, Dynamic Programming,
Quasi-Newton Method, Branch-and-Cut Method, Operating Point, Energy Losses, Linearization.
Abstract:
Minimizing the consumption of hydrogen by a fuel cell system in a hybrid vehicle can reduce its environmen-
tal impact and increase its autonomy. However an intelligent management of power distribution is essential to
meet the demand of the powertrain. The characteristics of the sources constituting the energy chain of the hy-
brid vehicle (efficiency and energy losses) make the mathematical model nonlinear. Solution methods such as
Dynamic Programming and Quasi-Newton which have so far been developed in previous works give satisfac-
tory results but with very large computation times. In this paper, a new combinatorial model is proposed and
a Branch-and-Cut method is developed to solve the problem to optimality. This approach leads to drastically
reduced computation times.
1 INTRODUCTION
Hybrid vehicles use at least two energy sources to
fuel their engines. The energy chain of the vehicle
concerned is composed of a Fuel Cell System (FCS)
which uses hydrogen to produce electrical energy
through the chemical reaction with oxygen, superca-
pacitors for energy storage characterized by their en-
ergy losses, and an electric motor (powertrain). The
challenge is to intelligently manage the power dis-
tribution by the two energy sources to meet the de-
mand of the powertrain with the goal of minimizing
the consumption of hydrogen by the FCS while re-
specting operational and safety constraints (Bernard
et al., 2010) (Caux et al., 2011). Several methods and
approaches such as dynamic programming (Brahma
et al., 2000) using Bellman principle, or the quasi-
Newton method (Guemri et al., 2012) have been de-
veloped on this subject. These methods give subopti-
mal results with very large computing time due to the
complexity of the underlying nonlinear problem and
discretization required. The objective of this study is
to improve the results obtained in previous work and
provide a decision as quickly as possible to start the
mission.
In the first part of this paper, the necessary back-
ground is given to highlight the model and solution
approaches developed in previous works. The sec-
ond part presents the new model and an application of
the Branch-and-Cut method on the problem. Finally
a third part is dedicated to the presentation of results
to evaluate the performance of the proposition.
2 THE ENERGY CHAIN
The energy chain is composed of a FCS connected to
the electric bus by an unidirectional converter, a pack
of supercapacitors connected in series and in paral-
lel to store energy which is also connected to the bus
via a bidirectional converter. The supercapacitor pro-
vides energy when the vehicle is in traction and stores
it when the vehicle brakes (principle of the transfor-
mation of kinetic energy into electrical energy).
The converter is an electronic power module
which generates a regulated output voltage. It serves
to maintain the bus voltage to its reference, despite
the power demands of the electric motor and changes
in voltage of the FCS and the supercapacitor. Its effi-
ciency is often very high ranging from 93% to 97%.
In reality, the FCS consists of the fuel cell itself
and its ancillaries (air compressor, pumps of tempera-
ture control and humidification). The power absorbed
253
Gaoua Y., Caux S. and Lopez P..
A Combinatorial Optimization Approach for the Electrical Energy Management in a Multi-source System.
DOI: 10.5220/0004203900550059
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 55-59
ISBN: 978-989-8565-40-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
by the air compressor depends on the power provided
by the FCS which represents 80% of the total power
consumed by the ancillaries.
0 10 20 30 40 50 60 70
0
5
10
15
20
25
30
35
40
45
50
FCS efficiency (%)
Power (kW)
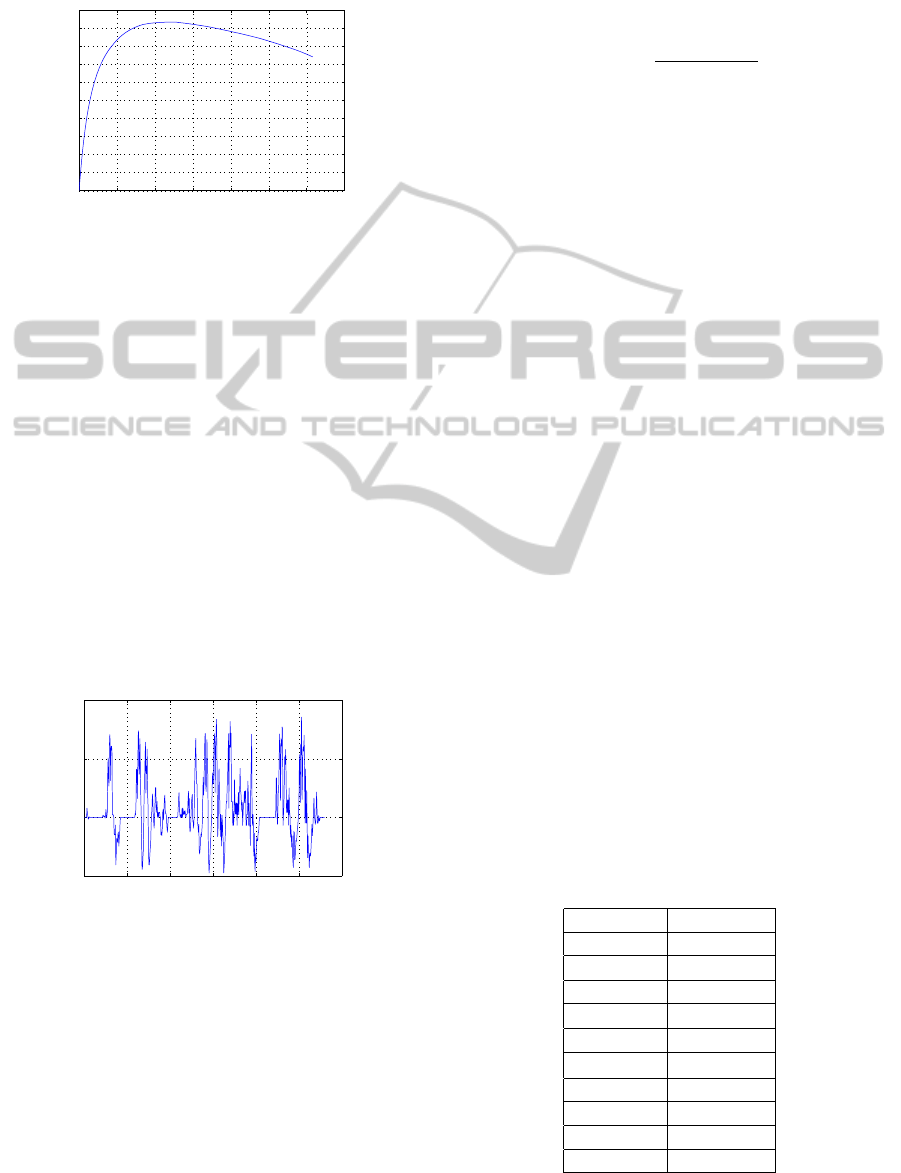
Figure 1: FCS efficiency.
Simulations and experiments (Caux et al., 2011)
showed that the maximum efficiency of the FCS used
with controlled pressure, temperature and humidity is
equal to 46.53% for a power of 22.28 kW, as shown
in Figure 1.
3 MATHEMATICAL
FORMULATION
To minimize the hydrogen consumption by the FCS
off-line, a mission profile provided by INRETS (Na-
tional REsearch Institute on Transport and their Secu-
rity) which corresponds to the instantaneous demand
required by the electric motor P
req
of a hybrid vehi-
cle in urban area on a period of T = 560s, is given in
Figure 2.
0 100 200 300 400 500 600
−50
0
50
100
Power demand (kW)
Time (s)
Figure 2: INRETS Mission profile.
The objective function is to minimize the hydro-
gen consumption P
h
, modeled as:
Minimize
T
∑
t=1
P
h
(t) ∆t (1)
where ∆t is a sampling time between two consecutive
instants.
The objective function can also be written in terms
of FCS efficiency η
fcs
whose function is determined
by a polynomial approximation and power supplied
P
fcs
, as shown in Equation 2. The nature of the FCS
efficiency function makes the objective function non-
linear (Figure 1).
Minimize
T
∑
t=1
P
fcs
(t)
η
fcs
(P
fcs
(t))
∆t (2)
The power provided by the FCS P
fcs
and the su-
percapacitor P
se
must meet the demand of the electric
motor when it is in traction, defined in Equation 3.
P
fcs
(t) + P
se
(t) = P
req
(t) (3)
Forcing the supercapacitor to recover all braking
energy can sometimes lead the FCS to work with a
poor efficiency, hence the importance of Constraint 4.
P
req
(t) ≤ P
se
(t) ≤ 0 (4)
The FCS is seen as a productionsource. It can pro-
vide a maximum power of P
max
fcs
(see Table 1) without
recovering in braking phases.
0 ≤ P
fcs
(t) ≤ P
max
fcs
(5)
The advantage of the supercapacitor is that it can
provide power and recover braking energy in the limit
of its capacity defined in Equation 6:
P
min
se
≤ P
se
(t) ≤ P
max
se
(6)
For energy storage, the state of charge of the su-
percapacitor SOC
se
at a given time is calculated based
on the previous state of charge and power provided
during this period of time:
SOC
se
(t) = SOC
se
(t) − P
s
(t)∆t (7)
The state of charge of the supercapacitor at each
time must not exceed its storage capacity defined by
an upper and lower bound (SOC
max
se
, SOC
min
se
):
SOC
min
se
≤ SOC
se
(t) ≤ SOC
max
se
(8)
Table 1: Input parameters of the model.
Parameter Value
SOC
se
(0) 900 kW.s
SOC
min
se
400 kW.s
SOC
max
se
1600 kW.s
P
min
se
−60 kW
P
max
se
60 kW
P
max
fcs
70 kW
T 560 s
∆t 1 s
I
fcs
601
J
se
2
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
254
By integrating the energy losses of the superca-
pacitor, the following constraint is imposed
P
s
(t) = P
se
(t) + Loss
se
(P
se
(t)) (9)
where P
s
is the real power supplied or recovered by
the supercapacitor and Loss
se
its energy losses func-
tion as shown in Figure 3.
−60 −40 −20 0 20 40 60
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Power (kW)
SE energy losses (kW)
Figure 3: Energy losses of the supercapacitor.
To allow the sequence of tasks in off-line opti-
mization without charging the supercapacitor artifi-
cially at the end of each mission, a condition is im-
posed on its final state of charge
SOC
se
(T) = SOC
se
(0) (10)
where SOC
se
(0) is the initial state of charge of the
supercapacitor.
4 BACKGROUND ON SOLVING
METHODS
In this section, the solution methods previously de-
veloped and applied to the energy management model
are presented.
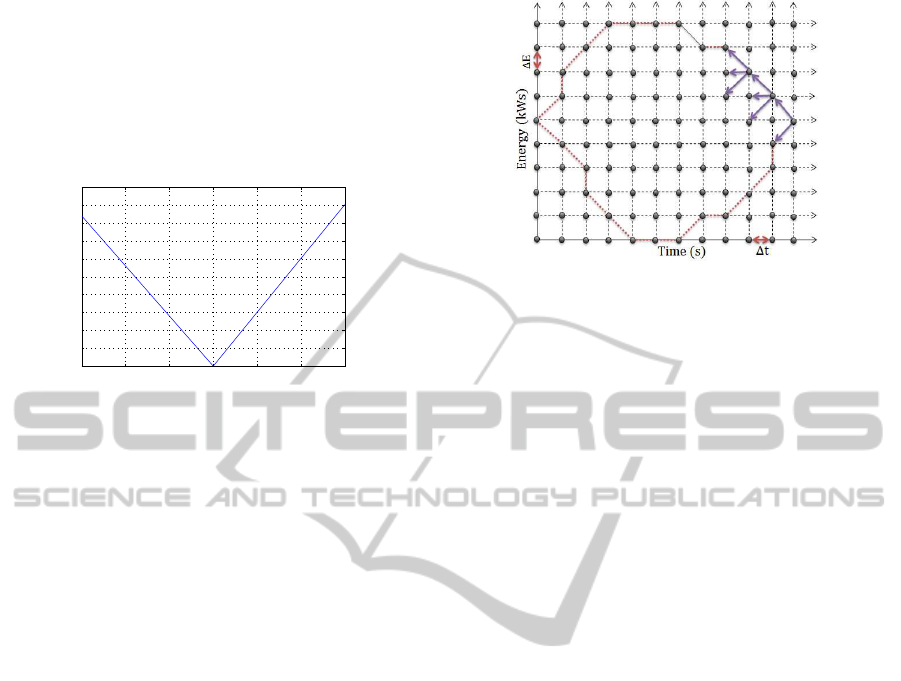
4.1 Dynamic Programming
Dynamic programming is a sequential combinatorial
optimization method for finding the optimal solution
using the Bellman principle: A sequence of decisions
is optimal if, regardless of the point considered, sub-
sequent decisions are a result of optimal decisions for
the sub-dynamic problem with this point as starting.
The discretization of the time horizon and the energy
space of the storage element (supercapacitor) are re-
quired to apply dynamic programming on the model
of the electric power management (P´erez et al., 2006).
The weakness of the application of dynamic pro-
gramming on the model of power management, is re-
lated to the discretization of the supercapacitor energy
space in N points of ∆E stepsize. Indeed, increasing
Figure 4: Dynamic Programming principle.
the number of possible states of charge of the super-
capacitor causes more choices and calculations to de-
termine the optimal sequence that minimizes the cri-
terion of hydrogen consumption. For a discretization
of the time horizon in ∆t =1 s and the energy space of
the supercapacitor in 1 kW.s, the optimal solution is
10131 kW.s, which corresponds to the hydrogen con-
sumed by the FCS on INRETS profile with a compu-
tation time of 22 hours. By decreasing the stepsize of
the supercapacitor energy space energy, the solution
will be improved but the computing time explodes.
4.2 Quasi-Newton Method
In numerical optimization, Quasi-Newton algorithm
is an iterative method for solving nonlinear prob-
lems by using Karush-Kuhn-Tucker conditions and
the calculation of the Hessian and the second deriva-
tive of the Lagrangian. The local minimum is found
when the gradient is zero. The solution found by
this method using fmincon function integrated in Mat-
lab Optimization toolbox, is a local optimum. After
the polynomial approximation of the two nonlinear
functions (FCS efficiency and supercapacitor energy
losses) by polynomials of degree 15 in order to reduce
errors of approximations, the consumption of hydro-
gen used by the FCS is 8750 kW.s, with a computation
time of 23 min (Guemri et al., 2012).
5 COMBINATORIAL MODELING
In the previous model, the objective function and the
function of the energy losses of the supercapacitor are
nonlinear and this makes finding an optimal solution
not guaranteed. The principle of this new modeling is
to work with the original data without using the ap-
proximations of the objective function and the energy
losses function.
Consider the operating point of the FCS i charac-
ACombinatorialOptimizationApproachfortheElectricalEnergyManagementinaMulti-sourceSystem
255

terized by its efficiency η
fcs
(i) and its energy supplied
P
fcs
(i), and I
fcs
the number of operating points of the
fuel cell system.
The decision variables used in the combinatorial
model are:
• X(t, i): Binary variables, activation or not of the
operating point i at time t,
• Y(t, j): Binary variables, activation or not of the
losses energy equation j at time t,
• P
se
(t): Power supplied or recovered by the super-
capacitor at time t,
• SOC
se
(t): State Of Charge of the supercapacitor
at time t,
• Elos
se
(t): Energy losses by the supercapacitor at
time t.
By integrating the operating points in the model,
the objective function becomes:
T
∑
t=1
I
fcs
∑
i=1
X(t, i)
P
fcs
(i)
η
fcs
(i)
∆t (11)
The capacity constraint of the FCS (Equation 5)
is removed, and the satisfaction demand constraint
when the vehicle is in traction (Equation 3) is replaced
by:
P
se
(t) +
I
fcs
∑
i=1
X(t, i)P
fcs
(i) = P
req
(t) (12)
knowing that one FCS operating point is actived at
each time t:
I
fcs
∑
i=1
X(t, i) = 1 (13)
Supercapacitor energy losses function is piece-
wise linear convex function (Figure 3) and can be
written as:
Elos
se
(t) = α
j
P
se
(t) + β
j
, P
se
(t) ∈ [γ
j
, γ
′
j
] (14)
where α
j
is the gradient of the line j and β
j
its inter-
cept over the interval [γ
j
, γ
′
j
]
To avoid the polynomial approximation, a formu-
lation using the max function is presented:
Elos
se
(t) =
J
se
max
j=1
α
j
P
se
(t) + β
j
(15)
where J
se
is the number of linear functions and j ∈ J
se
its index. This function can also be modeled as linear
equations system using binary variables and a big-M
constant:
Elos
se
(t) ≤ α
j
P
se
(t) + β
j
+ M(1− y( j, t)) (16)
Elos
se
(t) ≥ α
j
P
se
(t) + β
j
(17)
J
se
∑
j=1
y( j, t) = 1 (18)
The energy losses constraint (Equation 9) is re-
placed by:
P
s
(t) = P
se
(t) + ELos
se
(t) (19)
6 SOLVING AND SIMULATIONS
The branch-and-cut algorithm (Winston, 1994) used
to solve the model of energy management is an exact
hybrid method for combinatorial optimization. It inte-
grates cutting planes and branch and bound methods.
This method solves NP-hard problems effectively.
The principle of this method is to solve the relax-
ation of the integer linear problem using Simplex al-
gorithm. If the solution X
∗
found is feasible for the
integer linear problem then, this solution is optimal;
if not, a cutting plane method is applied (Papadim-
itriou and Steiglitz, 1982). The cutting plane method
consists of iteratively adding cuts violated by the so-
lution of the relaxed problem until no further cuts are
violated. The purpose of this method is to try to find
an integer optimal solution or reduce the domain of
non-integer values to start the branch-and-bound al-
gorithm (Rardin, 1998).
The branch-and-boundmethod is used to solve the
linear integer problem by separating the relaxed prob-
lem into two subproblems and evaluating their solu-
tions. The separation principle is to choose a non-
integer variable in the optimal solution of the relaxed
problem and separate it into two sub-problems by
adding the constraint x
i
≤ ⌊x
∗
i
⌋ to the first subprob-
lem, the constraint x
i
≥ ⌈x
∗
i
⌉ to the second, and solve
them with the Simplex method. This process is re-
peated until the optimal solution is found.
For solving, an exact branch-and-cut method is
applied using IBM − Ilog Cplex 12.4 and the optimal
solution was found, as shown in the following figures.
The consumption of hydrogen used by the fuel cell
system is 8750 kW.s with a computation time of 2.59
s.
The FCS supply power to the electric motor,main-
tains storage of the supercapacitor between its bounds
and recharges to its initial level at the end of the mis-
sion. As shown in Figure 5, the FCS is generally used
with high efficiency to minimize energy losses and
this explains the low consumption of hydrogen.
The supercapacitor recovers power to supply it
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
256
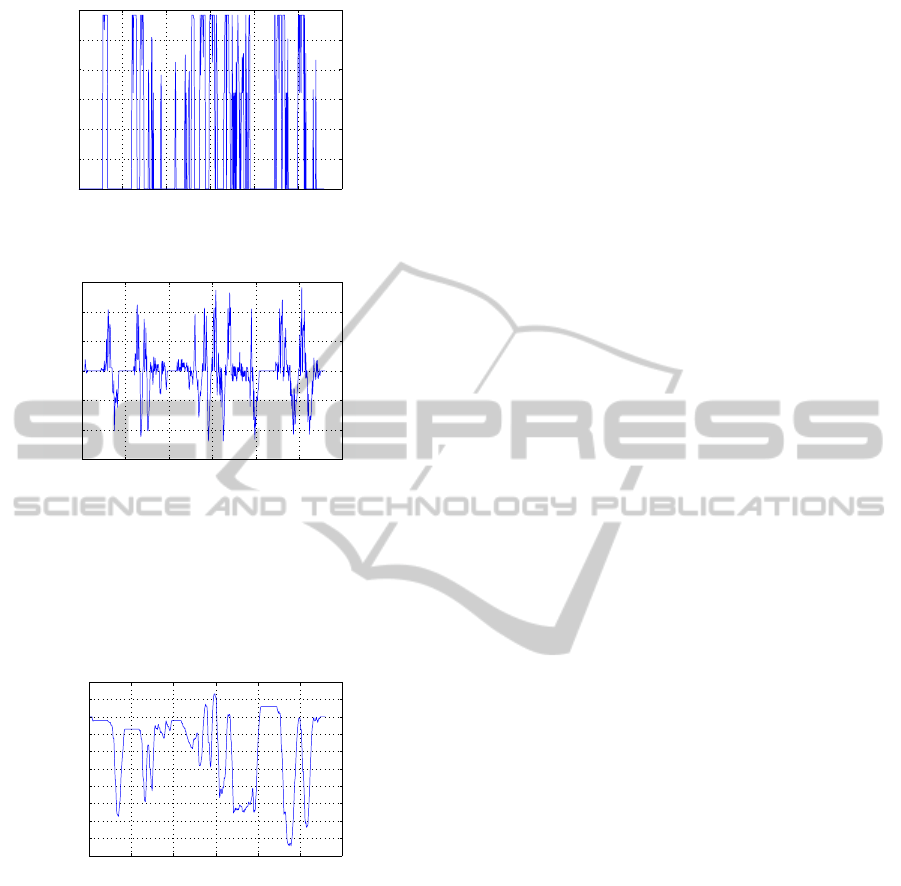
0 100 200 300 400 500 600
0
5
10
15
20
25
30
Time (s)
FCS power (kW)
Figure 5: Power provided by the FCS.
0 100 200 300 400 500 600
−60
−40
−20
0
20
40
60
Time (s)
SE power (kW)
Figure 6: Power provided/recovered by the SE.
when the vehicle is in traction (see Figure 6). Some-
times recovering all the braking energy is not a good
strategy because it forces the FCS to supply the rest
of the required power with low efficiency involving
energy losses.
0 100 200 300 400 500 600
500
550
600
650
700
750
800
850
900
950
1000
Time (s)
SE state of charge (kW.s)
Figure 7: State of charge of the SE.
In Figure 7, the storage capacity is respected and
the supercapacitor is reloaded to its original capacity
at the end of the mission.
7 CONCLUSIONS
The aim of managing distribution of electrical energy
is to meet the demand of the electric motor and also
to minimize the consumption of hydrogen by the fuel
cell. The methods previously developed can find sat-
isfactory solutions (suboptimal) but with very large
computation times. In reality, to start a multi-source
system such as a hybrid vehicle on a known trajec-
tory or mission profile, it is important to give quick
decisions to manage its energy distribution. The new
combinatorial model is efficient and it can find the op-
timal solution of the problem in a very short time.
REFERENCES
Bernard, J., Delprat, S., Guerra, T. M., and B¨uchi, F. N.
(2010). Fuel efficient power management strategy
for fuel cell hybrid powertrains. Control Engineering
Practice, 18(4):408–417.
Brahma, A., Guezennec, Y., and Rizzoni, G. (2000). Opti-
mal energy management in series hybrid electric vehi-
cles. In Proceedings of the American Control Confer-
ence, pages 60–64, Chicago, lllinois, USA.
Caux, S., Wanderley-Honda, D., Hissel, D., and Fadel, M.
(2011). On-line energy management for HEV based
on particle swarm optimization. The European Physi-
cal Journal Applied Physics, 54:1–9.
Guemri, M., Caux, S., and Ngueveu, S. U. (2012). Us-
ing quasi-Newton method for energy management in
electrical multi source systems. In 11th International
Conference on Environment and Electrical Engineer-
ing (EEEIC), pages 194–199, Venice, Italy.
Papadimitriou, C. H. and Steiglitz, K. (1982). Combi-
natorial Optimization: Algorithms and complexity.
Prentice-Hall.
P´erez, L. V., Bossio, G. R., Moitre, D., and Garc´ıa, G. O.
(2006). Optimization of power management in an
hybrid electric vehicle using dynamic programming.
Mathematics and Computers in Simulation, 73:244–
254.
Rardin, R. L. (1998). Optimization in operations research.
Prentice-Hall.
Winston, W. L. (1994). Operations research: Applications
and algorithms. Wadsworth.
ACombinatorialOptimizationApproachfortheElectricalEnergyManagementinaMulti-sourceSystem
257
