
Research of Classification Algorithms for Recognition of Digits
in Mechanical Counters
Dirk Benyoucef, Pirmin Held and Philipp Klein
Digital Communications & Signal Processing Lab, Furtwangen University,
Robert-Gerwig-Platz 1, 78120 Furtwangen, Germany
Keywords:
Electromechanical Counter, Pattern Recognition, Gray Scale Recognition, Classification, Bayes Classifier,
Support Vector Machine, Electricity Meter.
Abstract:
Mechanical counters are still very popular for their protection against manipulation and low costs. In the past
automatic readout of mechanical counters required complex and expensive image processing methods. The
system proposed in this paper is a cheaper alternative which does not require modifications to the mechanics
of the counter. The proposed system makes use of different light reflectivity parameters of the numbers shown
on the number wheels. In this paper the different approaches are shown and analyzed.
1 INTRODUCTION
Presently mechanical counters are very common
when a high degree of protection against manipula-
tion is required such as in counters for water, gas
or electricity consumption. Furthermore mechanical
counters are commonly used in cash and gaming ma-
chines. Since the costs are very high if persons have
to read out the counter value manually, methods for
automation of this process were developed in the past
years.
2 STATE OF ART
One system uses an electronic counter which has to
be fitted to the mechanical one. Unfortunately this
does not read out the actual value of the counter which
lessens the protection against manipulation.
There are different methods for the evaluation of
the optically sampled counter value. The method pro-
posed in this paper makes use of a pattern recognition
in gray scale values. It was described in (Benyoucef
et al., 2012). The emphasis of the paper (Benyoucef
et al., 2012) was on external influences such as scat-
tered light or temperature drifts. In contrast this paper
concentrates on the pattern recognition and enhance-
ments of the method.
Additionally other references committed to the
readout task are discussed in the following. As an
example Otsu proposed an evaluation method which
analyzed the resulting histograms of several images
(Otsu, 1979). A similar application is shown in
(Martinez-Carballido et al., 2011). In (Qian et al.,
2006) tried to detect the figures on banknotes. The
correct mapping of the measured gray values to the
figures is a classic problem of pattern recognition
which can be solved in different ways. While there are
several simple approaches such as distance or Bayes
classification there are also some more complex ones
such as support vector machines (SVM).
In 2010 Zhang et al. proposed a portable system
which allows for automatic readout of counter values.
The pattern recognition applies e.g. including mor-
phology, grayscale conversion, edge detection and the
Hough transformation (Zhang et al., 2010). Although
the system is able to read out the counter values a per-
son has to carry out the measurement by placing the
system on the counter because the system is very ex-
pensive.
Another system for automatic readout was pro-
posed by Shu et al. in 2007 (Shu et al., 2007). It
uses a digital image processing system for character
recognition.
The disadvantages of all methods discussed before
are that they are expensive, that they require modifica-
tion of the counter mechanics and that some of them
also require persons to carry out the readout manually.
The system proposed in this paper is much
cheaper because it consists of simple optoelectronic
parts and therefore allows for real automated process-
ing without requiring a person to start the readout.
522
Benyoucef D., Held P. and Klein P. (2013).
Research of Classification Algorithms for Recognition of Digits in Mechanical Counters.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 522-525
DOI: 10.5220/0004204305220525
Copyright
c
SciTePress

Furthermore it reads the actual counter value rather
than parallel counting with an electronic counter.
3 SYSTEM ANALYSIS
A test setup was built for a type of counters in or-
der to show that the proposed method is applicable.
Each figure wheel is illuminated by two LEDs. The
reflected light is measured by three photo transistors.
This setup results in a vector of measured values con-
sisting of nine dimensions.
Measurements showed how different external in-
fluences negatively affect the accuracy of the clas-
sification. Additionally to mechanical tolerances of
the counters temperature fluctuation or scattered light
have a negative effect on the classification. As shown
in (Benyoucef et al., 2012) temperature drifts and
scattered light intensity can be held as low as to al-
low for a correct classification of the figures on the
figure wheels.
The influence of mechanical tolerances during
production of the counters and printing of the figures
are much more critical because they result in char-
acteristic patterns for each figure, figure wheel, and
counter. Those patterns have to be trained to a classi-
fication algorithm which is a laborious task to do.
One important task is therefore to generalize the
measured values in order to require only one set of
training data for each type of counter.
For this generalization the classification results of
a distance classifier, a Bayes classifier assuming a sin-
gle or a double normal distribution, and an SVM in
a strongly vibrating environment, resulting in maxi-
mum mechanical play, are analyzed in section 5.
4 CLASSIFICATION METHODS
We now assume that a set of data containing known
pairs of figure wheel value and measured value is
available. This data is used to analyze different classi-
fication methods with respect to complexity and com-
putational efforts. For the latter efforts for training
and classification have to be analyzed separately. The
a priori information contained in our data set allows
for performance analysis of the algorithms.
Distance Classifier. The simplest approach is based
on a distance classifier. In Figures 1 (a) and (b)two
of the nine available dimensions of a measurement
of one figure are shown together with their respective
histograms. The plot in red shows a single normal dis-
tribution fitted to the data. The plot in green shows the
(a) Normal environment. (b) Vibrating environment.
Figure 1: Distribution of the figure 0 in two dimensions.
distribution function computed by the kernel density
estimation method (KDE).
Based on the fact, that the measured values show
either a single or double normal distribution (as
shown in Figures 1 (a) and (b)), and the assumption,
that the use of a double normal distribution leads to
only small errors when instead the data form a single
normal distribution, we always use the double normal
distribution.
The estimations of the distribution parameters is
done using the expectation maximization algorithm
(EM algorithm) (Dempster et al., 1977).
After analyzing all clusters a newly measured
value can be assigned to a figure by finding the min-
imum distance from the measured value to the sub-
cluster of the distributions of each figure.
Bayes Classifier with Single Normal Distributions.
Because of the disturbing influences described in
section 3 the variances of the individual clusters and
dimensions may differ. A distance classifier as de-
scribed before does not respect this fact which leads
to errors in heavily disturbed environments. In order
to improve the performance in this case we now ana-
lyze a Bayes classifier assuming a single normal dis-
tribution.
In contrast to the distance classification the Bayes
classifier includes the statistical characteristics of the
feature vector for the classification of the figures.
Starting point for the analysis is the feature vector x
m
which has to be classified. The Bayes classifier de-
cides in favor of the figure that maximizes its a poste-
riori probability
Bayes Classifier with Double Normal Distribu-
tions. In addition to the single normal distribution
we take a double normal distribution into account for
our analyzes. This is to improve classification results
of distributions like the one shown in Fig. 1 (b).
Support Vector Machines. Support vector ma-
chines are used for classification as well as for regres-
sion tasks. They are a mathematical method for pat-
ResearchofClassificationAlgorithmsforRecognitionofDigitsinMechanicalCounters
523

tern recognition developed by Cortes and Vapnic in
1995 (Cortes and Vapnik, 1995). The goal is to place
a separation plane between two clusters such that they
are separated by the largest distance possible.
In order to solve nonlinear classification problems
with this linear separation plane the data can be trans-
formed into a higher-dimensional space (theoretically
up to infinite dimensions) using a kernel function.
The advantage of SVM compared to Bayes classi-
fier is that they do not need to assume a distribution
function. The separation plane is placed such that the
distance of the measured values of each cluster closest
to the plane is maximal.
SVMs are only suitable for two-cluster situations.
The decision between 10 clusters, as it is the case for
counters, requires higher computation efforts. The ex-
tension to from two to 10 clusters was done using the
one against one (OAO) and the one against all (OAA)
methods. In the OAA case a radial basis function
(RBF) was used as a kernel function. In the OAO
case a linear, a polynomial and a radial basis func-
tion yielded equal results. Therefore the simple linear
kernel function was used.
5 EXPERIMENTAL RESULTS
In this section the results of the different classification
algorithms are shown. Figures 2 (a) and (b) show the
resulting errors. The horizontal axis is scaled in num-
bers of used dimensions. Since there are many differ-
ent ways of leaving some dimensions unanalyzed the
mean of all possibilities is plotted. The vertical axis
represents the classification error. The distance clas-
sifier is shown by the blue curve, the Bayes classifier
with a single normal distribution in green, the Bayes
classifier with a double distribution in red, the SVM
with OAA in turquoise, and the SVM with OAO in vi-
olet. The red bar marks the error level of 10
−4
which
can be achieved by the given number of training data.
First 25 training values were used for each figure.
The resulting number of errors is shown in Figure 2
(a). When the number of training values is increased
the number of errors decreases for all classifiers (Fig-
ure 2 (b)).
It can be seen that the SVM with the OAA method
produces more errors when using only few dimen-
sions than the other classifiers. The reason for this
is that the areas that cannot be classified nonambigu-
ously by the OAA method become relatively large. If
a measured value lies in this area it is marked as an
error. This is a disadvantage compared to the Bayes
classifier which does not apply a sharp separation line.
The best results are achieved by the SVM with the
(a) 25 training values. (b) 250 training values.
Figure 2: Resulting errors.
OAO method. This is more distinct when dealing with
few training values because the few values do not con-
tain enough statistical a priori information.
6 GENERALIZATION
6.1 Iterative Method using Gray Values
Until now the problem to solve was to assign gray val-
ues to a number considering only one measurement.
This leads to errors when training and test values re-
sult from different measurements. To demonstrate
this the number detection system is modeled as a Hid-
den Markov Model (HMM). The iterative method re-
quires the movement (increment or decrement) of the
figure wheel to be recognized. This movement can be
detected by computing the euclidean distance of two
measurements and applying a threshold detection af-
terwards. This movement detection is not part of this
paper; it is considered working correctly.
Usually the sequence of figures is known and
identical among different types of counters. This
knowledge can be used for the classification of mea-
sured gray values. Although the sequence of figures
is determined this model does not describe the value
change events as these depend on the actual system
the counter is used in. After a first measurement the
probability that the measured gray values describes a
figure can be computed. Once a movement of the fig-
ure wheel is detected, this process is repeated yielding
in a series of probabilities. In contrast to the methods
described before the iterative method then classifies
the counter value according to the maximum of the
product of this probability sequence.
6.2 Iterative Method using Differences
of Gray Values
Another way to improve the classification accuracy
is to use differences of reflectivity values. This way
offsets due to severals reasons including ambient tem-
perature can be eliminated. This is especially advan-
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
524
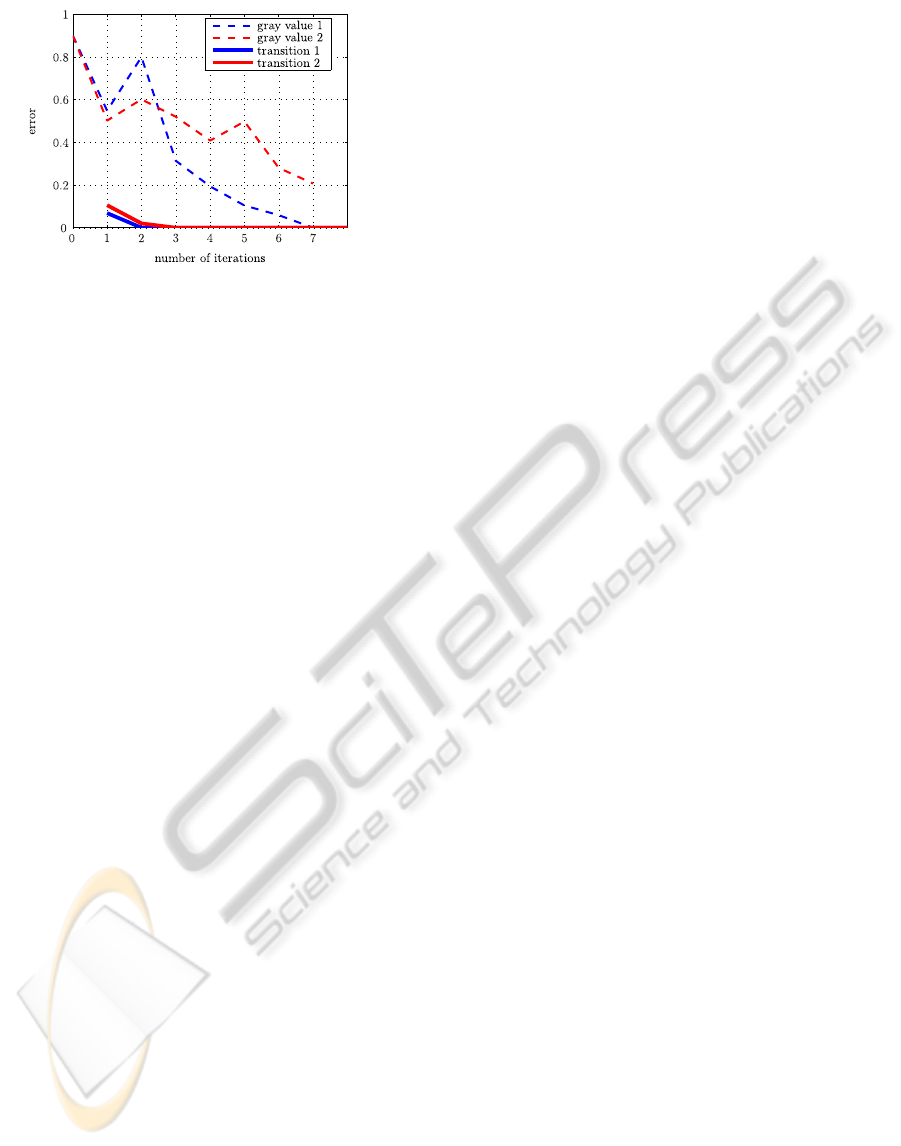
Figure 3: Resulting errors vs. sequence length for two
counter wheels.
tageous for the generalization of the training values
for different types of counters. The difference is di-
rectly computed in the 9-dimensional feature space.
In order to classify a figure sequence the reflectiv-
ity values of at least two consecutive figures are re-
quired. A longer sequence will lead to a higher prob-
ability of correct classification of this sequence.
In Figure 3 the resulting errors are plotted against
the sequence length for two different figure wheels.
The dashed lines represent the errors of the direct
gray value classification. The errors of the classifica-
tion of transitions are shown by the continuous lines.
For this example 5000 reflectivity values measured at
an ambient temperature of 20
◦
C were analyzed. The
4000 training values were measured at 0
◦
C on a dif-
ferent counter. It can easily be seen that the error rate
decreases with increasing sequence length. Also the
difference between the direct gray value classification
and the classification of reflectivity value differences
is directly visible. This effect is especially distinc-
tive due to the combination of test and training val-
ues described above. The temperature difference be-
tween training and test measurement leads to an offset
which is eliminated by computing the differences of
gray values.
In conclusion the direct gray value classification
yields good results when good-natured training and
test values are used (cf. the sections above). If though
training and test measurements are subject to differ-
ent ambient conditions the analysis of differences of
reflectivity values is advantageous.
7 CONCLUSIONS
In this paper a system for reading out a mechanical
counter automatically was presented. It is based on
the fact that different counter values have different
light reflectivity coefficients. The main advantage is
that the counter does not have to be modified and that
the simple electronics are very cheap. This method
can also be applied during the manufacturing of the
counters in order to do a quality control test. The in-
fluence of external parameters can be reduced to such
levels that a very precise classification of the figures
can be achieved.
The different classification methods can be chosen
according to desired application and available compu-
tation resources. The iterative method opens another
application area. It allows for the analysis of different
counters using one set of training data. An increas-
ing number of counter value changes increases the
chances of its correct recognition. If, instead of direct
gray values, differences of reflectivity values are used
offsets due to temperature and other influences can be
eliminated. Since this method is especially useful for
recognition of different counters of the same type this
may be interesting for counter manufactures for post-
production testing.
REFERENCES
Benyoucef, D., Held, P., and Bier, T. (2012). Icounter - de-
velopment of an optical readout method for mechan-
ical counters. International Conference on Pattern
Recognition Applications and Methods (ICPRAM).
Cortes, C. and Vapnik, V. (1995). Support-vector networks.
Machine Learning.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum Likelihood from Incomplete Data via the
EM Algorithm. Blackwell Publishing.
Martinez-Carballido, J., Alfonso-Lopez, R., and Ramirez-
Cortes, J. (2011). License plate digit recognition us-
ing 7x5 binary templates at an outdoor parking lot en-
trance. In Electrical Communications and Computers
(CONIELECOMP), 2011 21st International Confer-
ence. IEEE.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Transactions on systems, man
and cybernetic.
Qian, J., Qian, D., and Zhang, M. (2006). A digit recogni-
tion system for paper currency identification based on
virtual instruments. In ICIA 06. IEEE.
Shu, D., Ma, S., and Jing, C. (2007). Study of the automatic
reading of watt meter based in image processing tech-
nology. In Industrial Electronics and Applications,
2007. ICIEA 2007. 2nd IEEE Conference. IEEE.
Zhang, Z., Chen, G., Li, J., Ma, Y., and Ju, N. (2010). The
research on digit recognition algorithm for automatic
meter reading system. In Intelligent Control and Au-
tomation (WCICA), 2010 8th World Congress. IEEE.
ResearchofClassificationAlgorithmsforRecognitionofDigitsinMechanicalCounters
525
