
Visualizing Temporal Behavior in Multifield Particle Simulations
T. S. Reis Santos
1
, F. V. Paulovich
1
, V. Molchanov
2
, L. Linsen
2
and M. C. F. de Oliveira
1
1
Instituto de Ci
ˆ
encias Matem
´
aticas e de Computac
˜
ao, University of S
˜
ao Paulo, S
˜
ao Carlos, Brazil
2
School of Engineering and Science, Jacobs University, Bremen, Germany
Keywords:
Volume-based Particle Visualization, Time-varying Visualization, Multidimensional Projection.
Abstract:
Particle-based simulations generate time-varying multifield volumetric datasets. Visualizations of such vol-
umes traditionally focus on the physical space, displaying particles as glyphs or with volume rendering tech-
niques. In this paper we deal specifically with the issue of helping users to observe and interpret the multidi-
mensional feature space and its temporal behavior, as a complement to existing spatial views. Our approach
combines multiple visualizations to assist analysis of time-varying data generated by particle simulations. Co-
ordinated views of both feature and physical spaces allow the observation of particle behavior over specific
time periods or the whole temporal domain, rather than describing a single simulation time step. Temporal
behavior in the physical space is depicted as pathlines, whereas the temporal behavior of the underlying mul-
tidimensional feature space is depicted in a so-called streamfeature visualization. Streamfeatures are pathlines
describing changes in feature space along time, obtained by projecting the feature vectors. Direct interaction
with these line representations is difficult. Thus, two supporting views are supplied for user interaction, which
show 2D projections of both the pathlines (pathline projection view) and the streamfeatures (streamfeature
projection view), obtained by projecting geometric features extracted from the lines. By linking all visual-
izations, users may interact with these views to identify and select representative clusters of lines that reflect
similar behavior of particle features. We use data from two particle simulations to illustrate the framework and
its potential to support analysis of global temporal behavior and relationships between multiple variables.
1 INTRODUCTION
Computer simulations allow the study of phenom-
ena that cannot be observed in real life, e.g., nu-
clear simulations or simulations of collisions between
stars. Particle-based techniques are widely employed
in many domains, describing real-world phenomena
as systems of discrete particles that have certain prop-
erties. Millions of particles may be required to ac-
curately capture system behavior, thus generating
very large datasets that are typically time-varying and
multi-attribute, as multiple simulation variables de-
scribe each particle.
Assisting data analysis in this scenario is challeng-
ing, and several high-quality visualization techniques
and approaches have been proposed. Most existing
solutions focus on representing particles in the physi-
cal space, i.e., in the spatial domain of the simulation,
at specific time steps. They usually rely on volume
rendering solutions, or display particles as glyphs,
and temporal behavior is observed from a sequence
of such representations. In multivariate simulations,
it is likely that users also want to observe the feature
(or attribute) space defined by the multiple variables
describing particle behavior. A multidimensional fea-
ture space may be visualized with techniques such
as Parallel Coordinates (Inselberg, 1985), scatterplot
matrices or multidimensional projections (Joia et al.,
2011; Poco et al., 2011; Paulovich et al., 2010), which
have been employed to complement spatial views in
multifield volume rendering (Blaas and Post, 2008;
Linsen et al., 2008; Linsen et al., 2009; Akiba and
Ma, 2007).
In this work we focus on tools for visualizing
the feature space in particle simulations, employ-
ing multidimensional projections in a framework that
allows observing how the underlying feature space
evolves. Central to this framework is a line glyph
called a streamfeature, designed to convey temporal
behavior of a particle and reveal meaningful changes
in its defining feature space. The streamfeature
line is obtained by concatenating particle projections
generated for a sequence of simulation time steps.
By displaying views of the streamfeatures, we con-
tribute an approach to observe time-varying volumet-
ric datasets derived from multifield particle simula-
573
S. Reis Santos T., V. Paulovich F., Molchanov V., Linsen L. and C. F. de Oliveira M..
Visualizing Temporal Behavior in Multifield Particle Simulations.
DOI: 10.5220/0004207705730582
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (IVAPP-2013), pages 573-582
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

tions in which: (i) particle behavior is observed by co-
ordinating views of both feature and physical spaces
(streamfeatures and pathlines, respectively); (ii) sim-
ilarly to the well-known pathlines in fluid visualiza-
tion, the streamfeature glyph conveys the global tem-
poral behavior of each particle, as observed in its
defining attribute space. Thus, both physical and fea-
ture space visualizations embed multiple simulation
time steps.
This paper is organized as follows. Section 2 dis-
cusses related work on visualizing time-varying data
generated by particle simulations. Section 3 provides
a short background on multidimensional projection
techniques used in this work. The computation of
the streamfeature glyph is explained in Section 4.
Section 5 describes the framework that incorporates
the streamfeature visualization, how it is linked with
alternative views and functionalities for data explo-
ration. Section 6 describes usage of the framework to
explore data from two particle simulations, and finally
Section 7 presents conclusions and further work.
2 RELATED WORK
(Gribble et al., 2006) introduce a GPU-based ap-
proach to generate visualizations of very large particle
simulation datasets, focusing on generating 3D views
on desktop computers at interactive rates. Their so-
lution renders high quality particle glyphs using point
sprite rendering and software-based acceleration tech-
niques. It supports several data exploration functions
and is fast enough to handle multiple time-varying
volumes, but apart from interactivity it offers no spe-
cific support for analysis over the temporal domain.
(Falk et al., 2010) also propose an efficient solu-
tion for rendering the physical space. They imple-
ment a method of sliced ray casting with on-demand
volume reconstruction that combines texture slicing,
ray casting and splatting. The density field is recon-
structed from the particles in screen space at viewport
resolution and at the sampling depths used by the vol-
ume ray casting. This solution requires less memory
than an object-space ray casting and achieves supe-
rior image quality and comparable rendering perfor-
mance.
(Co et al., 2004) are interested in interactive ex-
ploratory tools for simulation data in the domain of
particle accelerator physics, seeking for solutions ca-
pable of depicting views of the feature space. Their
suite of tools integrate 2D and 3D scatterplots and a
representation of the particles as 3D-shaped glyphs
aimed at conveying shape and trends in particle dis-
tributions affected by multiple electromagnetic fields.
Animation conveys temporal behavior. Authors em-
phasize that the combination of familiar small mul-
tiple scatterplots for rapid multidimensional data ex-
ploration with selection and linked views to facilitate
visual correlation of similarity results in an effective
system for exploratory tasks.
Recent contributions specifically address visual-
ization of time-varying multivariate data and exploit
the idea of integrating visualizations of both the phys-
ical (object) space and the feature (attribute) space.
This is the case of the system by (Jones et al., 2008)
to handle time-varying multivariate point-based data
from gyrokinetic simulations. The feature space visu-
alization, called variable visualization, shows the re-
lationships and trends among the multiple simulation
variables and provide an intuitive interface for select-
ing data items. The object space, or physical visual-
ization, shows a spatial representation of the particles
as spherical glyphs (with point sprite rendering) at a
single time step, and as illuminated pathlines along a
range of time steps, with line color and opacity map-
ping a user selected variable. The variable view is
based on an optimized implementation of Parallel Co-
ordinates with brushing and alternative locking modes
as enhanced facilities for users to specify selections in
multidimensional space. All views are linked, so user
selections on the Parallel Coordinates reflect in the
physical and other views. The Parallel Coordinates
view depicts variable relations at a single time step
– for multiple time steps authors use 2D x −y plots
of the different variables, with the x-axis representing
time.
Our work has many elements in common with
that of (Wei et al., 2012), who propose a dual-space
visualization approach for studying particle combus-
tion simulation data. By ”dual space” they refer to
a combination of the 3D simulation domain in which
the particles are advected, referred to as the physical
space, and the attribute domain, in which the particle
attributes evolve, called the phase space. The parti-
cle’s spatial movement in physical space is called its
trajectory, and its attribute variation in phase space is
called its attribute evolution curve. The system incor-
porates user-driven semi-supervised learning to deal
with the difficulties of handling and interacting with
the large bulk of lines. The attribute evolution curves
are clustered using a polynomial regression mixture
model, and users can interact with groups to identify
and categorize interesting behavior.
We also employ trajectory lines to depict parti-
cle behavior in both physical and attribute spaces, in-
spired by the approach adopted by (Poco et al., 2012)
to handle brain fiber tracking data. Authors extract
shape features from the 3D lines describing the fibers
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
574

in order to generate 2D layouts which separates the
lines based on similarity of their global shape. The
layout provides an alternative visual interface that fa-
cilitates interaction with the fiber lines: by linking
both views, bundles of lines with similar behavior
may be user selected and further inspected. We gener-
ate line icons that summarize particle behavior in at-
tribute space over time, as well as projections of such
lines to help users to identify and interact with rele-
vant groups of lines. The same approach is applicable
to pathlines that describe particle behavior in physical
space.
3 BACKGROUND
Our framework relies on dimension reduction with
multidimensional projection. Let X be a set of n
data points defined in a d-dimensional space, i.e.,
X = {x
0
, x
1
, ..., x
n
}, with x
i
= {x
i
1
, x
i
2
, ..., x
i
d
} ∈ R
d
.
Let Y denote the projection of X in a visual space (R
2
or R
3
). s(·, ·) is a dissimilarity function criterion be-
tween two data points in R
d
and ˆs(·, ·) is their dissimi-
larity function criterion defined in the projected space.
A multidimensional projection is a technique that ob-
tains Y from X, given s(·, ·), usually while attempting
to minimize some error measure defined in terms of s
and ˆs.
Many approaches may be applied to project high-
dimensional data, e.g., one may obtain visual repre-
sentations with classical dimension reduction tech-
niques such as Principal Component Analysis (Jol-
liffe, 2002) or Fastmap (Faloutsos and Lin, 1995) on-
sidering the 2 or 3 best ranked principal components,
or projecting the data points x
i
∈ X in p mutually or-
thogonal directions with p = {2, 3}.
The Force Scheme (FS) (Tejada et al., 2003)
projection adapts the classical Force-Directed Place-
ment (FDP) strategies. It reduces computational cost
by considering the pairwise distances between data
points, rather than computing forces on a mass-spring
model. An initial layout – random or computed with
another projection method – is iteratively modified to
separate data points projected too close and bring to-
gether those placed too far apart, according to an error
measure given by the difference between s and ˆs, i.e.,
the ideal and the actual pairwise point distances.
Handling time-varying volumes requires tech-
niques capable of handling large datasets and
generating temporally coherent projections. The
Part-Linear Multidimensional Projection (PLMP)
(Paulovich et al., 2010) and the Local Affine Multidi-
mensional Projection (LAMP) (Joia et al., 2011) are
recent solutions that meet such requirements.
The mathematical formulation of PLMP may be
seen as a generalization of PCA. A linear transforma-
tion mapping to obtain Y from X is inferred from a
mapping previously applied to a subset of representa-
tive data points. Representatives should be chosen to
reflect data density and distribution. According to the
authors taking
√
n random samples is usually a rea-
sonable choice, as the technique is robust to the choice
of representatives. PLMP has complexity O(n) and
good precision measured by stress values computed
for layouts generated for several datasets. Moreover,
because its transformation mapping is computed from
a reduced subset of points, PLMP is applicable as a
streaming projection, as not all data points need to be
known a priori.
LAMP also relies on selecting and projecting a
subset of samples, known as control points, from
which it builds a family of orthogonal mappings, one
for each data point. Users can manipulate the place-
ment of the control points to obtain a satisfactory
layout. A reduced number of control points usually
suffices to obtain good visual mappings, and albeit
slower than PLMP and Fastmap LAMP is also com-
petitive in terms of computational times.
Deciding the best technique to project a dataset
is not straightforward, and several quantitative mea-
sures help to assess the quality of a layout. They usu-
ally attempt to capture to which extent a layout re-
tains the distance distribution observed in the input
data space. The well-known Kruskal stress measure
(Kruskal, 1964), given by equation (1), attempts to
quantify the information loss incurred in the projec-
tion mapping.
Kruskal =
s
∑
i< j
( ˆs(x
i
, x
j
) −s(x
i
, x
j
))
2
∑
i< j
ˆs(x
i
, x
j
)
(1)
One may alternatively inspect a scatterplot of the
original distances × pro jected distances for all data
point pairs, known as stress curve (Joia et al., 2011).
A hypothetically ideal projection that achieves 100%
distance preservation would produce a stress curve
with all points plotted along the main diagonal line
in the scatterplot.
The Neighborhood Preservation (NP) curve
(Paulovich et al., 2008), on the other hand, displays
the percentage of neighboring points in the input
space that remain in the same neighborhood after the
projection, for a varying number of neighbors. This
value is computed for each data point and averaged
over all data points (see Figure 4).
VisualizingTemporalBehaviorinMultifieldParticleSimulations
575
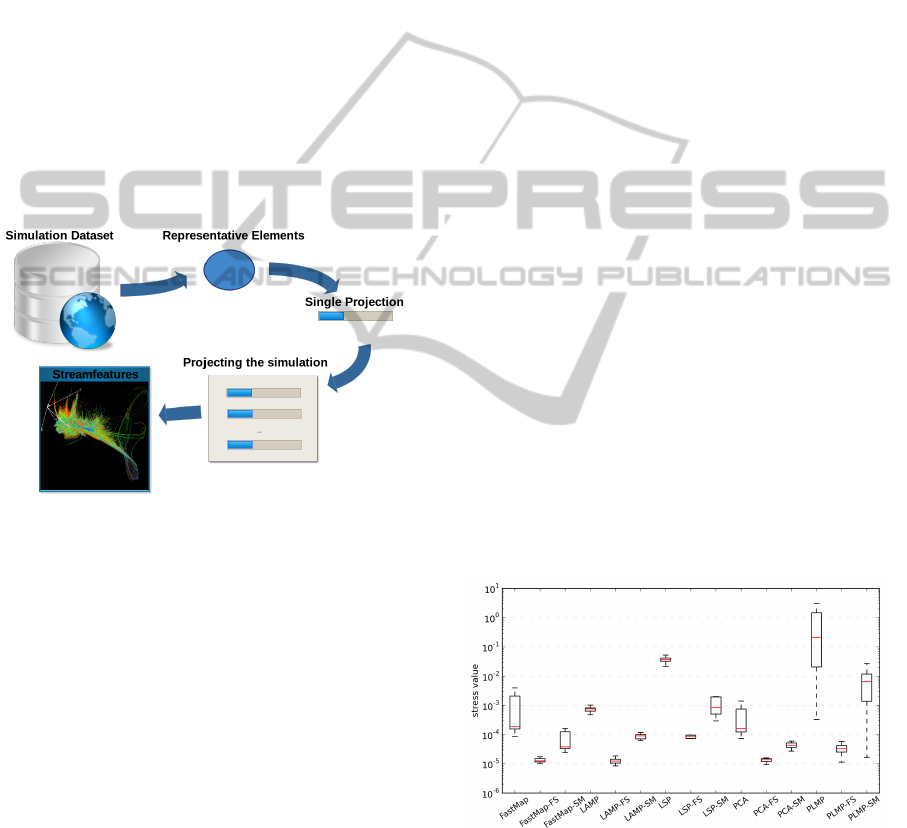
4 GENERATING PARTICLE
STREAMFEATURES
A streamfeature is created for a particle by projecting
its feature vectors extracted from a temporal sequence
of volumes and connecting the projected points into a
line. This line describes the particle’s temporal evolu-
tion, as observed in its defining feature space. Projec-
tion may be performed with either PLMP or LAMP,
as both have the capability of preserving temporal and
spatial coherence when handling time series data. As
discussed in Section 3, both techniques require se-
lecting and projecting a representative subset of data
points, and the quality of this initial projection af-
fects the quality of the overall result. We thus em-
pirically investigate multiple alternatives, taking the
quality measures described in Section 3 as guides to
identify the potentially best choice, given a dataset.
Figure 1: Pipeline of the streamfeature generation process.
Generating streamfeatures comprises three stages,
illustrated in Figure 1. Initially, it may be necessary
to downsample the volumes for the sequence to fit the
primary memory available. This is done by random
sampling. The subset of representative data points
(required by both PLMP and LAMP) is obtained by
taking a random sample from each volume. The rep-
resentatives’ feature vectors must be then projected
with a precise technique. Several techniques and dis-
tance functions may be considered for this initial pro-
jection, and we compare the quality of different lay-
outs to make an informed choice.
We projected the representatives with the classi-
cal techniques PCA, Fastmap, Sammon’s Mapping
and the Force Scheme (Tejada et al., 2003), as well
as with recent ones known to be fast and precise,
namely LAMP, PLMP and LSP (the Least Squares
Projection) (Paulovich et al., 2008). Both Sammon’s
Mapping and Force gradually optimize an initial lay-
out based on an error criterion, so alternative initial
layouts may be considered. Overall we investigated
15 projection or dimension reduction techniques and
variations – Fastmap, Fastmap with Force Scheme
(meaning the former provided an initial layout for the
latter), Fastmap with Sammon’s mapping, PCA, PCA
with Force Scheme, PCA with Sammon’s mapping,
LAMP, LAMP with Force Scheme, LAMP with Sam-
mon’s mapping, PLMP, PLMP with Force Scheme,
PLMP with Sammon’s mapping, LSP, LSP with Force
Scheme, LSP with Sammon’s mapping – and distance
functions, Euclidean and Mahalanobis, as approxi-
mations to dissimilarity s(·,·). Euclidean is a usual
choice, and Mahalanobis is known to be effective in
normally distributed data with multiple correlated at-
tributes (Tan et al., 2005).
We compare the layouts obtained regarding stress
function values, stress curves and neighborhood
preservation capability, in order to select the best
projection of the representatives for either PLMP or
LAMP. In the final stage the remaining particles (the
non-representatives) at each time step are projected in
3D, and the projected points relative to a single par-
ticle are connected into a line to obtain its streamfea-
ture.
Figures 2 and 3 show box plots of the mean stress
values computed for the layouts generated to obtain
the streamfeatures for a dataset analyzed in Section 6,
considering the Euclidean and the Mahalanobis dis-
tances, respectively. The Euclidean layouts with low-
est stress are Fastmap with Force Scheme, LAMP
with Force Scheme and PCA with Force Scheme;
for Mahalanobis are Fastmap, Fastmap with Force
Scheme and Fastmap with Sammon’s Mapping have
the lowest values. Notice that the layouts obtained
with Mahalanobis have lower stress values in general.
Figure 2: Kruskal stress of 15 layouts computed with dis-
tinct techniques and Euclidean distance, for a particular
dataset. Best: LAMP-FS, Fastmap-FS and PCA-FS.
The stress curves of the best layouts obtained with
both Euclidean and Mahalanobis distances, not shown
due to space constraints, indicate that they all do a
very good job of preserving original distances, with a
slight superiority of the Mahalanobis layouts on this
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
576
Figure 3: Kruskal stress of 15 layouts (same dataset and
techniques) now with the Mahalanobis distance. Best:
Fastmap, Fastmap-FS and Fastmap-SM.
Figure 4: Neighborhood preservation curves of the best lay-
outs (best stress values) computed with Euclidean (top) and
Mahalanobis (bottom).
particular dataset.
Figure 4 shows the Neighborhood Preservation
curves for the three best (according to stress values)
layouts, with the Euclidean (a) and the Malahanobis
distances (b). We actually compared the curves for
all the layousts, and observed that the techniques with
best stress values also display the best behavior re-
garding neighborhood preservation.
All in all, the layout created with Fastmap with
Force Scheme and the Mahalanobis distance attained
the best stress and better neighborhood preservation,
and is thus a good choice as the initial layout of the
representatives in computing the particle streamfea-
tures for this dataset. A similar comparative analysis
should be conducted for any dataset. Streamfeature
visualizations generated for different simulations are
illustrated in Section 6.
5 VISUALIZATION
FRAMEWORK
The framework developed integrates four distinct
views to assist interpretation of temporal data. Two of
them are the streamfeature and pathline views, both il-
lustrated in Figures 7 and 11, in Section 6, for two dis-
tinct simulations. The high density of lines makes it
difficult to interact directly with those views, however.
We employ multidimensional projections of both the
streamfeatures and the pathlines as complementary
views to support user interaction, as illustrated in Fig-
ure 6. Users may interact with those views to iden-
tify and select groups of streamfeatures or pathlines
for further inspection, as illustrated in the case stud-
ies discussed in Section 6. The projections convey
similarity relations over the temporal domain and,
as such, help identification of temporal clusters and
trends. They also afford interactions such as selection
of one or multiple streamfeatures or pathlines. All
four views are linked, so that interaction in a projec-
tion view, e.g., a selection is reflected in the remaining
views.
Projecting the streamfeatures or pathlines requires
describing them as multidimensional feature vectors.
As our goal is to highlight paths with similar global
and local shapes and geometric properties – e.g., start-
ing point, size – so as to reveal similar behavior in fea-
ture space, features must be chosen that encode such
information. Following the same rationale adopted
by (Poco et al., 2012), our feature vectors are formed
by low and high frequency coefficients of the Fast
Fourier Transform (FFT) of the 3D line (Reddy and
Chatterji, 1996), in each principal direction (x, y, z),
plus the line’s initial and final positions, its size and
its center of mass.
The resulting vector is described by 40 attributes:
30 Fourier coefficients (15 low-frequencies in x, y and
z; 15 high-frequencies in x, y and z,) plus 10 geo-
metrical coefficients, namely the (x, y, z) coordinates
of the starting point, idem for the final point and the
center of mass point, plus the line size. This choice
places a dominance of shape attributes (Fourier coef-
ficients) over the geometric ones. A more balanced
distribution of shape and geometric attributes may be
desirable depending on the goals, e.g., if the goal is to
favour perception of similar line shapes in nearby re-
gions. It is thus possible to vary the weights assigned
to the features prior to projection. In the examples
discussed in Section 6 the line features were projected
VisualizingTemporalBehaviorinMultifieldParticleSimulations
577

with LAMP.
Users may select individual elements or groups in
the projection views, and track the selection in the
pathline and streamfeature views. They can manu-
ally identify groups of particles with similar behavior
by delimiting visual clusters in the projection, or al-
ternatively an X-means clustering (Pelleg and Moore,
2000) may be applied to identify clusters automati-
cally. This is an extension of k-means clustering that
finds the optimal number of clusters that best models
the data, within a given range. Once obtained, clusters
are color coded in the projection, as illustrated in Fig-
ure 6. Users may select one or multiple clusters and
inspect their behavior in the pathline or streamfeature
feature projection views. The ability to interact with
groups is particularly useful, as the original line views
are typically very cluttered. Users may also choose to
observe behavior over a time range, rather than over
the whole simulation time.
6 EXPLORING SIMULATION
DATA
We illustrate the techniques on data derived from
Smoothed Particle Hydrodynamics (SPH) simula-
tions (Linsen et al., 2011) and made available by
collaborators, identified as the Merging Stars and
the Exploding Stars datasets. Both datasets rep-
resent binary star systems consisted of two White
Dwarfs each. Simulations include thousands of time
steps, of which only a small part is used for analy-
sis and visualization. Several scalar and vector fields
are recorded, including physical quantities (velocity,
gravity, mass, etc.), chemical fractions and computa-
tional parameters (radius of influence of particle, arti-
ficial viscosity coefficient and others).
6.1 Merging Stars
In this simulation one of the modeled objects (the
donor star) is being destroyed when its mass gradually
flows to the second star (accretor) under strong grav-
itational force. Two White Dwarfs are discretized by
means of 2.5M particles carrying the following scalar
quantities: radius of influence, density, temperature,
and artificial viscosity.
As discussed in Section 4, the streamfeatures view
for these data have been created using Fastmap with
Force Scheme to project the representatives, LAMP
and the Mahalanobis distance. The streamfeatures
view relative to the whole simulation is shown in
Figure 5. The multidimensional axes describing the
streamfeature space are shown displaced. In this and
Figure 5: Streamfeatures for the whole simulation and axes
in 9-dimensional attribute space (Exploding Stars).
Figure 6: X -means clusters in the projection view. The pink
cluster has been selected and its elements are shown high-
lighted (thicker borders).
in the following figures that adopt the rainbow scale,
color mapping indicates time evolution: blue corre-
sponds to initial stages of the simulation, and red in-
dicates final stages. The Cartesian axes in the four-
dimensional attribute space have undergone the same
projection transformation applied to the data, and pro-
vide a visual hint of the attributes undergoing domi-
nant changes in the temporal domain and the direc-
tion of change – from the figure one observes that at-
tributes density (axis 2) and artificial viscosity (axis
4) are dominant in the temporal domain.
The streamfeatures and pathlines were projected
with LAMP using the Mahalanobis distance, but the
resulting layouts are very dense and cluttered, ham-
pering perception of groups of similar elements. The
result of applying an X-means clustering to both pro-
jections can be seen in Figure 6, which depicts the
5 clusters identified – we input a range [5, 50] for
the number of clusters to be sought for by X-means.
We computed the silhouette coefficients of the result-
ing clusterings. This is a measure of cluster qual-
ity (Tan et al., 2005) that takes values in the range
[−1.0, 1.0], where values closer to 1.0 indicate well
separated and highly cohesive groups. Silhouette val-
ues of 0.416 and 0.799 were obtained for the pathline
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
578
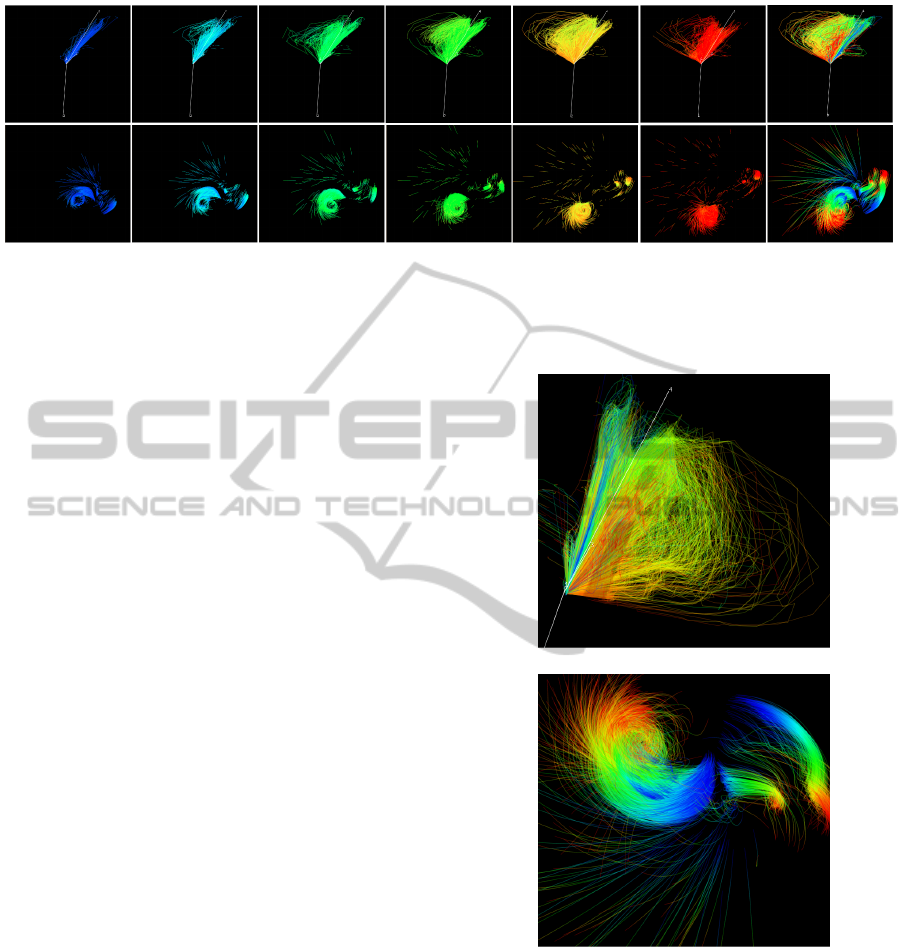
Figure 7: Merging Stars simulation: top row images show the streamfeatures describing the behavior of a selected cluster of
particles, bottom row images show the corresponding pathlines. The rightmost images cover the whole simulation (59 time
steps), whereas the previous ones show streamfeatures and pathlines computed over a sequence of size 10 time windows,
namely 0-10, 10-20, 20-30, 30-40, 40-50 and 50-59. Most particles are moving towards the center of the two stars, and one
observes little variation occurring in the direction of attribute density (axis 2, the long vertical line in the central region).
and the streamfeature clusters, respectively. The sec-
ond value indicates well-formed clusters that group
similar-shaped streamfeature lines, as measured by
the Mahalanobis distance. Thus, they likely depict
similar particle trajectories in feature space.
Figure 7 shows evolution of the particles in the
pink cluster selected in Figure 6, with blue to red map-
ping time evolution. This particular cluster has 2,007
particles, or 1.61% of the total particles tracked. The
top row shows images of the streamfeatures and the
bottom row shows the corresponding pathlines, com-
puted over different simulation time periods. Inter-
preting a visualization that covers the whole temporal
domain is not straightforward, it may thus be inter-
esting to observe behavior over shorter time intervals,
e.g., as shown in the figure, over windows of size 10,
corresponding to 10 simulation time steps.
The pathlines in Figure 7 indicate that particles in
this group are being attracted to the center of the two
stars. In the streamfeature views we notice that major
changes occur in the directions associated to attributes
radius (axis 1), temperature (axis 3) and artificial vis-
cosity (axis 4), while no major changes are observed
in the direction associated to attribute density (axis
2) for this particular cluster. Furthermore, notice that
changes were initially localized around the direction
defined by attribute artificial viscosity (4), but then
from time interval 40-50 the attributes radius (1) and
temperature (3) start playing a more dominant role
in particle behavior. Figure 8 shows rotated views of
the rightmost images in Figure 7, illustrating possible
user interactions with these 3D representations.
6.2 Exploding Stars
In the second simulation, extremely high tempera-
tures are reached during stars interactions. This serves
as an indicator for the start of nuclear burning that
(a) Streamfeatures view.
(b) Pathlines view.
Figure 8: Rotated views of the visualizations in the last col-
umn of Figure 7 (Merging Stars).
later will – although this phase has not been simu-
lated and is not presented in the data – lead to the
explosion of stars. This simulation tracks 39,200 par-
ticules and the number of attributes is 13, of which 9
were chosen for analysis. They are: radius of influ-
ence, internal energy, temperature, several chemical
components, and the mean number of nucleons per
isotope (“abar”).
The streamfeatures have been generated employ-
VisualizingTemporalBehaviorinMultifieldParticleSimulations
579
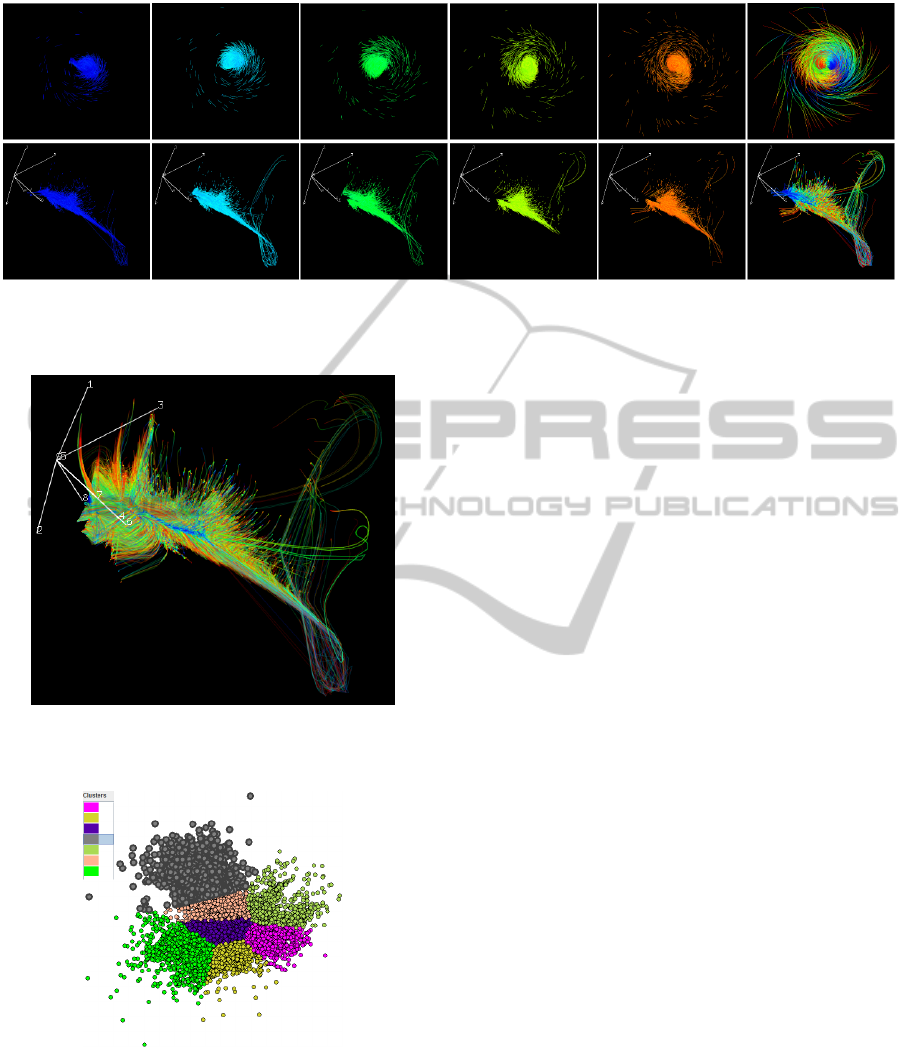
Figure 11: Pathlines (top) and streamfeatures (bottom) of a selected cluster in the Exploding Stars simulation. The rightmost
images display the streamfeatures and pathlines computed over the whole simulation (200 time steps). Left to right: a
sequence of streamfeatures and pathlines for time windows of size 20, namely 0-20, 40-60, 80-100, 120-140 and 160-180.
Figure 9: Streamfeatures for the whole simulation, shown
with axes in 9-dimensional attribute space (Exploding
Stars).
Figure 10: X-means clusters in the streamfeature feature
projection, with a cluster selected and highlighted.
ing Fastmap with Force Scheme, LAMP and the Ma-
halanobis distances as the dissimilarity functions, af-
ter considering several alternatives and conducting an
analysis similar to that detailed for the Merging Stars
data. The resulting streamfeatures for the whole sim-
ulation are shown in Figure 9.
The projection of the features extracted from the
streamfeatures, computed with LAMP and Maha-
lanobis, appears in Figure 10, with clusters color
coded. X -Means identified 7 clusters as the best con-
figuration (searching in the range [5, 50]). The com-
pued silhouette coefficient is 0.482, indicating clus-
ters not as well-formed as in the previous example.
Figure 11 shows the evolution of the cluster se-
lected in Figure 10, which includes 6,883 particles,
17.56% of the total. Images in the top row depict
the particle pathlines and in the bottom row the corre-
sponding streamfeatures are shown. One notices that
some particles in this group are trapped in the gravita-
tional field of the star, those seen in the central circular
shape in the pathline views, whereas others seem to
escape the star attraction and are lost to space, shown
by the pathlines tangent to the circular shape. As
the simulation starts the major directions of change
seem to be associated with attributes Helium, Neon
and Magnesium (axes 4, 6 and 7, respectively), at-
tributes radius and temperature apparently start play-
ing a major role as it evolves (notice the outgoing lines
at the right region of the streamfeature views).
An interface widget is provided for users to filter
the pathlines to be displayed according to their size,
by setting lower and upper size thresholds. This al-
lows them to focus, e.g., on analyzing a subset of par-
ticles with greater (or smaller) displacement in the ob-
ject space. Visualizations after such filtering are illus-
trated in Figure 12: they cover the whole simulation,
but shown are only lines that survived the filtering.
Each column shows a view of the pathlines (top) and
the corresponding streamfeatures (bottom).
From left to right, images in the first column dis-
play the object and feature space behavior of 3 par-
ticles, then 12, 441 and 1,880 particles, respectively:
the first three views show only particles with high dis-
placement, whereas the last one shows particles with
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
580
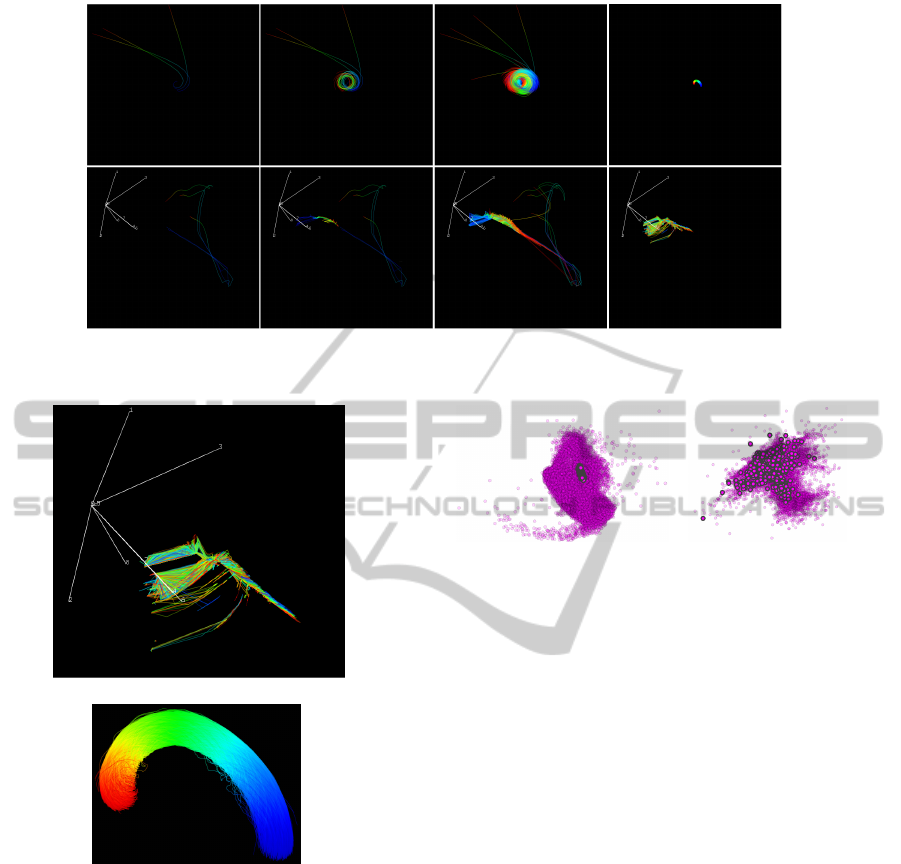
Figure 12: A view of the pathlines (top) and streamfeatures (bottom) filtered by their size. From left to right, images display
the object and feature space behaviors of 3, 12, 441 and 1,880 particles, respectively, along the Exploding Stars simulation.
(a) Streamfeatures.
(b) Pathlines.
Figure 13: Observing behavior of 1,880 particles filtered
based on their spatial displacement: particles with small
displacement.
low displacement. One observes that most particles
show reduced spatial displacement, highly concen-
trated in the central region, whereas the three parti-
cles with higher displacement wander away from this
central area.
Behavior of the 1,880 particles with small spatial
displacement in the simulation is better observed in
the views in Figure 13. Figure 14 shows projected
views of the features extracted from the pathlines and
the streamfeatures, highlighting the particles filtered.
(a) Pathline projection. (b) Streamfeature projec-
tion.
Figure 14: Projections of the streamfeature and pathline
features: 1,880 low-displacement particles highlighted.
7 CONCLUSIONS
We developed a framework to support the exploratory
visualization of data generated by multifield particle
simulations. This is a challenging problem that re-
quires handling a temporal sequence of multi-attribute
volumes and assessing and interpreting time-varying
multidimensional information. Our framework inte-
grates visualizations of both the spatial (physical) and
the feature space domains, and includes functional-
ities for users to observe and interpret particle tem-
poral behavior in both spaces simultaneously. This
is achieved by combining multiple coordinated views
of both feature and physical spaces to allow the ob-
servation of particle behavior over the whole tempo-
ral domain or over selected time windows, rather than
restricting users to handling a single simulation time
step.
The feature space visualization relies on an ana-
log of the well-known pathlines for visualizing fluid
behavior. This view suffers with overcrowding as
the number of particles increases, quickly aggravated
when handling simulations over many time steps.
This is handled with clustering and filtering function-
alities and with projected representations of feature
VisualizingTemporalBehaviorinMultifieldParticleSimulations
581

vectors extracted from the lines. Usage of the frame-
work has been illustrated on data from two SPH sim-
ulations in astrophysics. We intend to investigate fur-
ther the feature extraction procedures adopted to gen-
erate the projection views of pathlines and stream-
features, as other alternatives might produce differ-
ent outcomes. Distortion errors are likely introduced
in the projection processes, and how they affect ex-
ploration of temporal behavior also deserves a careful
investigation, in line with validation of the framework
in cooperation with domain experts.
ACKNOWLEDGEMENTS
Authors acknowledge the financial support of
FAPESP, CNPq, CAPES-DAAD-PROBRAL, DFG
under contract number LI 1530/6-2 and are grateful
to S. Rosswog and M. Dan, from Jacobs University,
Bremen, Germany, for the simulation datasets.
REFERENCES
Akiba, H. and Ma, K.-L. (2007). A tri-space visualization
interface for analyzing time-varying multivariate vol-
ume data. In Proc. Eurographics/IEEE VGTC Symp.
Visualization, pages 115–122.
Blaas, J. and Post, C. P. B. F. (2008). Extensions of par-
allel coordinates for interactive exploration of large
multi-timepoint data sets. IEEE Trans. Vis. Computer
Graphics, 14(6):1436–1451.
Co, C. S., Friedman, A., Grote, D. P., Vay, J.-L., Bethel,
Wes, E., and Joy, K. I. (2004). Interactive methods for
exploring particle simulation data. Lawrence Berkeley
National Laboratory.
Falk, M., Grottel, S., and Ertl, T. (2010). Interactive image-
space volume visualization for dynamic particle sim-
ulations. In SIGRAD.
Faloutsos, C. and Lin, K.-I. (1995). FastMap. In Proc. ACM
SIGMOD Int. Conf. Management of Data, pages 163–
174, New York, New York, USA. ACM Press.
Gribble, C. P., Stephens, A. J., Guilkey, J. E., and Parker,
S. G. (2006). Visualizing particle-based simulation
datasets on the desktop. In British HCI Works. on
Combining Visualization and Interaction to Facilitate
Scientific Exploration and Discovery, pages 111–118.
Inselberg, A. (1985). The plane with parallel coordinates.
The Visual Computer, 1(2):69–91.
Joia, P., Paulovich, F. V., Coimbra, D., Cuminato, J. A.,
and Nonato, L. G. (2011). Local affine multidimen-
sional projection. IEEE Trans. Vis. Computer Graph-
ics, 17(12):2563–71.
Jolliffe, I. T. (2002). Principal Component Analysis.
Springer.
Jones, C., Ma, K.-L., Ethier, S., and Lee, W.-L. (2008). An
integrated exploration approach to visualizing multi-
variate particle data. Computing in Science and Engi-
neering, 10(4):20–29.
Kruskal, J. B. (1964). Multidimensional scaling by opti-
mizing goodness of fit to a nonmetric hypothesis. Psy-
chometrika, 29(1):1–27.
Linsen, L., Long, T. V., and Rosenthal, P. (2009). Linking
multi-dimensional feature space cluster visualization
to surface extraction from multi-field volume data.
IEEE Comp. Graph. and Applications, 29(3):85–89.
Linsen, L., Molchanov, V., Dobrev, P., Rosswog, S., Rosen-
thal, P., and Long, T. V. (2011). Hydrodynamics -
Optimizing Methods and Tools, chapter SmoothViz:
Visualization of Smoothed Particles Hydrodynamics
Data. inTech.
Linsen, L., Van Long, T., Rosenthal, P., and Rosswog,
S. (2008). Surface extraction from multi-field parti-
cle volume data using multi-dimensional cluster vi-
sualization. IEEE Trans. Vis. Computer Graphics,
14(6):1483–90.
Paulovich, F. V., Nonato, L. G., Minghim, R., and Lev-
kowitz, H. (2008). Least square projection: a fast
high-precision multidimensional projection technique
and its application to document mapping. IEEE Trans.
Vis. Computer Graphics, 14(3):564–75.
Paulovich, F. V., Silva, C. T., and Nonato, L. G. (2010).
Two-phase mapping for projecting massive data sets.
IEEE Trans. Vis. Computer Graphics, 16(6):1281–90.
Pelleg, D. and Moore, A. (2000). X-means: Extending k-
means with efficient estimation of the number of clus-
ters. In Proc. 7th. Int. Conf. Machine Learning, pages
727–734. San Francisco.
Poco, J., Eler, D., Paulovich, F., and Minghim, R. (2012).
Employing 2d projections for fast visual exploration
of large fiber tracking. Comput. Graph. Forum,
31(3):1075–1084.
Poco, J., Etemadpour, R., Paulovich, F., Long, T., Rosen-
thal, P., Oliveira, M., Linsen, L., and Minghim, R.
(2011). A framework for exploring multidimensional
data with 3D projections. Comput. Graph. Forum,
30(3):1111–1120.
Reddy, B. S. and Chatterji, B. N. (1996). An FFT-based
technique for translation, rotation, and scale-invariant
image registration. IEEE Trans. Image Processing,
5(8):1266–71.
Tan, P.-n., Steinbach, M., and Kumar, V. (2005). Introduc-
tion to Data Mining. Addison Wesley, Boston, MA.
Tejada, E., Minghim, R., and Gustavo Nonato, L. (2003).
On improved projection techniques to support visual
exploration of multi-dimensional data sets. Informa-
tion Visualization, 2(4):218–231.
Wei, J., Yu, H., Grout, R., Chen, J., and Ma, K.-L. (2012).
Visual analysis of particle behaviors to understand
combustion simulations. IEEE Comput. Graph. Appl.,
32(1):22–33.
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
582
