A New Evaluation Framework and Image Dataset for Keypoint

Extraction and Feature Descriptor Matching

nigo Barandiaran

1,2

, Camilo Cortes

1,3

, Marcos Nieto

, Manuel Gra

and Oscar E. Ruiz

Vicomtech-IK4 Research Alliance, San Sebasti

an, Spain

Dpto. CCIA, UPV-EHU, San Sebasti

an, Spain

CAD CAM CAE Laboratory, Universidad EAFIT, Carrera 49 No 7 Sur - 50, Medell

ın, Colombia

Keywords:

Keypoint Extraction, Feature Descriptor, Keypoint Matching, Homography Estimation.

Abstract:

Key point extraction and description mechanisms play a crucial role in image matching, where several image

points must be accurately identiﬁed to robustly estimate a transformation or to recognize an object or a scene.

New procedures for keypoint extraction and for feature description are continuously emerging. In order to

assess them accurately, normalized data and evaluation protocols are required. In response to these needs, we

present a (1) new evaluation framework that allow assessing the performance of the state-of-the-art feature

point extraction and description mechanisms, (2) a new image dataset acquired under controlled afﬁne and

photometric transformations and (3) a testing image generator. Our evaluation framework allows generating

detailed curves about the performance of different approaches, providing a valuable insight about their be-

havior. Also, it can be easily integrated in many research and development environments. The contributions

mentioned above are available on-line for the use of the scientiﬁc community.

GLOSSARY

I : Set of images

: Image n of set I

: pixel position in I

of a keypoint in R

: Homography that maps pixels of I

to I

d(a, b) :

a − b

1 INTRODUCTION

Several computer vision-based applications rely on

keypoint matching. Depending on the nature of such

applications, the requirements for a speciﬁc keypoint

extractor and descriptor may vary. For example, ap-

plications related with self-navigation or simultane-

ous location and mapping (SLAM) require a fast key-

point extractor algorithm because of their real-time

restrictions. On the other hand, an application for ob-

ject or image recognition beneﬁts from a more robust

keypoint descriptor; even if this implies a higher com-

putation time.

A keypoint is a distinguished point in R

repre-

senting the projection of a particular structure of a 3D

scene. A feature descriptor is a vector in R

that

contains a set of attributes that intend to uniquely rep-

resent x

Currently, there is an increasing activity in the

development of new approaches for keypoint extrac-

tion, description and matching, pursuing robustness

and low computational complexity. In order to assess

these new approaches accurately, normalized data and

evaluation protocols are required.

Responding to the mentioned needs, in this paper

we present a new evaluation framework for the eval-

uation of the state-of-the-art keypoint extractors and

feature point descriptors.

Formally, the framework discussed here has the

following I/O speciﬁcation:

INPUTS: (1) A set I =

{

, I

, . . . , I

}

captured from

a particular scene. (2) A set of bijection functions



1,2

, f

1,3

, . . . , f

i, j

, . . .



, such that f

i, j

: I

→ I

es-

tablishes the real correspondence between pixels of

and I

, so that mapped pixels actually mark the

same 3D point. (3) A set of matching algorithms

A =

{

, A

, . . . , A

}

. Algorithm A

is an arbitrary

conﬁguration of a keypoint extraction approach and

a feature description technique. A

produce an alter-

native set of functions S

when applied on I, which

match the images of I among themselves. The set S

is the ground-truth data of I, since it is the set of map-

252

Barandiaran I., Cortes C., Nieto M., Graña M. and Ruiz O..

A New Evaluation Framework and Image Dataset for Keypoint Extraction and Feature Descriptor Matching.

DOI: 10.5220/0004211502520257

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 252-257

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

pings corresponding to reality. The set of functions

is considered imperfect, since it resembles the ac-

tual set S

OUTPUTS: A set of performance evaluations for the

matching algorithm A

(1 ≤ m ≤ w). These perfor-

mance evaluations obviously grade the quality of A

against the ground-truth data. This appraisal allows

measuring several algorithm’s features, such as re-

peatability, accuracy and invariance to afﬁne or pho-

tometric transformations.

In addition, this article reports the protocol for

producing a particular set I under controlled afﬁne

and photometric transformations. The capture has

been conducted using a methodology that allows to

ensure that only one kind of transformation occur for

a series of images. This permits to determine how

sensitive is A

to a speciﬁc factor. In order to supple-

ment the dataset of real images, we present an image

generator that allows producing images with afﬁne or

photometric transformations for testing purposes.

The research community and the practitioners on

computer vision applications can obtain valuable in-

formation from the mentioned contributions to im-

prove their approaches or to select the algorithm that

best suit their needs.

2 RELATED WORK

Tuytelaars et al. suggested that there are several

parameters of a point detector and feature descriptor

that can be measured to assess their performance

(Tuytelaars and Mikolajczyk, 2008). However, to

measure some of them, such as the point extrac-

tor accuracy, descriptor robustness or invariance

a normalized test protocol and test benchmark

are required. In this way, the seminal works of

Mikolajczyk et al. settled the basis for keypoint

extractor and feature description evaluations (Miko-

lajczyk and Schmid, 2005). Since then, several

new approaches for keypoint or region extraction

(Mikolajczyk et al., 2007) and for feature description

(Bay et al., 2006; Heikkil

a et al., 2009; Bellavia

et al., 2010; Leutenegger et al., 2011) were tested

against their dataset and evaluated with their corre-

sponding scripts, which are freely available online at

www.robots.ox.ac.uk/ vgg/research/afﬁne/index.html.

Recently, Gauglitz et al. proposed a dataset of sev-

eral videos of surfaces, with different types of textures

and different light conditions, which are used to eval-

uate keypoint matching strategies oriented to camera

tracking applications (Gauglitz et al., 2011). The au-

thors claim that due to restrictions of the hardware

they used to move the camera for the generation of

different points of view, they could not reproduce ex-

actly the same movements every time they changed

scene conditions. This implies that the evaluation of a

particular factor may not be performed given the dif-

ferences in the geometric transformations during the

acquisition of I.

Very recently, Alahi et al. (Alahi et al., 2012)

tested their descriptor approach with the dataset and

evaluation framework of Mikolajczyk and Schmid

(Mikolajczyk and Schmid, 2002). However, they also

tested their descriptor with a non-publicly accessi-

ble approach in computer-vision-talks.com, which is

similar to our evaluation framework proposal. This

framework allowed the authors to compare the ro-

bustness of their descriptor against different geomet-

ric transformation values, in the form of a ratio be-

tween correct and wrong matches. The authors afﬁrm

that this approach provides a very useful insight about

the tested descriptors.

Important contributions have been performed to

assess the performance of the extraction and match-

ing mechanisms using non-planar scenes. Fraun-

dorfer and Bischof (Fraundorfer and Bischof, 2005)

proposed an extension of the work of Mikolajczyk

and Schmid (Mikolajczyk and Schmid, 2005) by an-

alyzing keypoint repeatability for non-planar scenes.

They used tri-focal tensor geometric restriction for es-

timating the ground-truth data of their own dataset.

Other relevant works in this ﬁeld are presented by Gil

et al. (Gil et al., 2010) and Moreels et al. (Moreels

and Perona, 2007).

Our dataset and evaluation framework are inspired

by the developments of Mikolajczyk and Schmid

(Mikolajczyk and Schmid, 2005). In comparison to

that approach, our contribution comprises a higher

number of images, with higher resolution and with

better controlled conditions, and it is supplemented

with an image generator. For the acquisition of im-

ages we used different types of sensors, including mo-

bile devices. It is important to consider some features

of these devices, such as their low dynamic range, in

a testing data. To the best of our knowledge, this fea-

ture lacks in the available testing datasets. Our dataset

present variations in both geometric (e.g. similarities

and afﬁnities) and photometric transformations (e.g.

luminance and chrominance noise addition).

Finally, our evaluation framework is written in

C++, which makes its integration in development

environments straightforward, and allows generating

detailed curves about the performance of different ap-

proaches.

All presented material in this work, i.e., images,

code and binary executables will be freely available

on-line at www.vicomtech.tv/keypoints.

ANewEvaluationFrameworkandImageDatasetforKeypointExtractionandFeatureDescriptorMatching

253

3 EVALUATION FRAMEWORK

We have implemented an evaluation framework based

on the one present in the Open Source Computer

Vision Library (OpenCV) (Bradski, 2000). It uses

the class hierarchy implemented in OpenCV that de-

couples keypoint extraction from keypoint descrip-

tion and descriptor matching, allowing to try differ-

ent conﬁgurations of keypoint extractor, descriptors

and matchers. Whereas Mikolajczyk’s work (Miko-

lajczyk and Schmid, 2005), where the framework is

written in Matlab scripting, our approach is written

in C++, allowing its easy integration in a develop-

ment environment. Thus, is not necessary to ex-

port additional data to other platforms, as occurs with

the mentioned Matlab-based evaluation framework,

which can be can be cumbersome, especially when

developing commercial software. Nevertheless, our

approach also supports the reading of Mikolajczyk’s

ﬁle format, allowing the comparison with previous

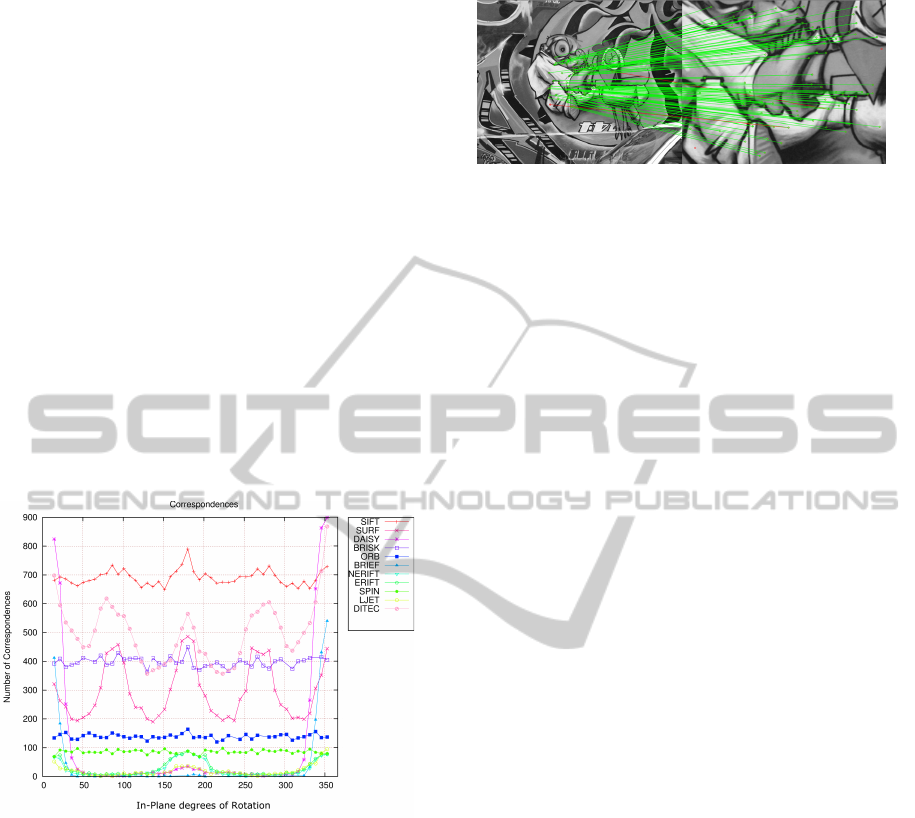
approaches or studies. Figure 1 shows partial results

Figure 1: Results of the evaluation of several feature de-

scriptors using the in-plane rotation.

of an evaluation conducted using our dataset and eval-

uation framework. In addition to the precision-recall

curves proposed by Mikolajczyk and Schmid (Miko-

lajczyk and Schmid, 2002), our framework generates

detailed performance curves based on the number of

correct matches given speciﬁc values of the evaluated

transformation. For example, Figure 1 shows the re-

sult of the number of correct matches of several fea-

ture descriptors against a dataset composed of several

in-plane rotations of an image. They suggest that, for

example, BRIEF descriptors are not robust against a

rotation larger than 35 degrees approximately. Also,

it can be observed that SURF approach is more sensi-

tive to orientations like 90, 180 and 270 degrees, pos-

sibly due to discretization effects related with the use

of box ﬁlters for approximating LoG ﬁltering. In this

Figure 2: Correct matches (in green), wrong matches (in

red) between two images.

way, a better insight of the behavior of a given ap-

proach can be obtained.

3.1 Matching Evaluation

An image formation process is usually represented as

in Equation 1 where Y

represents a point in R

and

corresponds to the projection of Y

in the image. P

represents the projection matrix, described in Equa-

tion 2, where K describes the transformation from the

camera reference frame to the image reference frame,

and [R|t] the composition of a translation and a rota-

tion transformation between world and camera coor-

dinate systems.

= PY

(1)

P = K[R|t] (2)

When either points Y

lie on a plane, or the images

are acquired with a camera rotating around its center

of projection, the transformation among points y

and

points Y

corresponds to a 2D linear projective trans-

formation or homography H (Hartley and Zisserman,

2004).

As in the dataset proposed by Mikolajczyk and

Schmid (Mikolajczyk and Schmid, 2002), a 2D ho-

mograhpy relate all images in our set I. This known

transformation is used as ground truth data, allowing

to know a priori where x

should be projected in I

by using Equation 3.

= H

(3)

Similarly, keypoints from I

can be projected back

to I

by using the inverse of H

. Let ˜x

be the esti-

mated match of x

obtained by a given A

. Then, H

is used to measure the accuracy and repeatability of a

point detector algorithm. This process is performed

by computing the error measure d

i j

of the estimated

and the ground truth keypoints of a pair of images, as

shown in Equation 4.

i j

= d( ˜x

, H

)

+ d(x

, H

−1

˜x

)

(4)

In order to estimate correct matches m

of key-

point pairs x

and ˜x

, as shown in Figure 2, we used

the overlap error deﬁned by equation 5 to reduce the

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

254

Figure 3: Image acquisition setup with Kuka robotic arm

and Canon 7D attached.

probability of occurrence of false positive matches

(Mikolajczyk and Schmid, 2002). Consider two el-

lipsoidal support regions R

and R

estimated by a

point extraction algorithm. The error in equation 5

measures how well the supporting regions correspond

under the geometric transformation H

= 1 −



∩ H

∪ H



(5)

We calculate the ellipses overlap by using the soft-

ware proposed by Hughes and Chraibi (Hughes and

Chraibi, 2011), which is available at www.chraibi.de.

If point pair x

and ˜x

present an error measure

i j

given by equation 4 and overlap error given by

equation 5 under some predeﬁned thresholds, then it

is considered as a correspondece.

4 IMAGE DATASET

4.1 Acquisition Setup

Our image acquisition setup is composed by a DSLR

Canon 7D and an iPad with a 5 Mega pixels built-in

camera. In the Canon 7D scenario we used a Tam-

ron 17-50mm f2.8 and a Canon 100mm f2.8 macro

lenses. In addition to the camera, we used two Canon

580EXII ﬂash with light diffuser, both operated wire-

lessly and synchronized with the acquisition. In the

case of the iPad setup we can not synchronize the light

with the acquisition, so we decided to use continuous

light source instead of ﬂashes.

4.2 Geometric Transformations

In order to generate a set of images with different val-

ues of perspective distortion, we used a Kuka robotic

arm with a Canon 7D attached with Tamron lens (see

ﬁgure 3) to obtain several points of view of a tar-

get scene by traversing circular trajectories (arcs), as

shown in Figure 4. The robot allowed us to gener-

ate known, repeatable and precise poses and trajec-

tories around the target scene, as an improvement to

the manual acquisition described by Gauglitz et al.

(Gauglitz et al., 2011). To generate and command

the follow up of the desired trajectories, we developed

an application in C++, which uses the Kuka Fast Re-

search Interface to interface with the robot.

We used a Wacom Cintiq screen for displaying

the target images, instead of using pictures placed in

a wall or in a table as performed by Gauglitz et al.

(Gauglitz et al., 2011). Our set of displayed images

covers different types of images with structured, un-

structured and low texture, as well as repeating pat-

terns. Several authors (Tuytelaars and Mikolajczyk,

2008; Heikkil

a et al., 2009; Gauglitz et al., 2011)

agree in the importance of evaluating keypoint extrac-

tors and descriptors in different conditions to truly test

their robustness.

The described trajectories are resampled accord-

ing to a desired number of points M, along them,

where images are to be taken. The set Q =

{

, Q

, . . . , Q

}

constitutes the resulting discretized

trajectory. Each Q

∈ Q is 3x4 matrix that describes

the i-th (1 ≤ i ≤ M) desired pose of the camera with

respect to the robot’s base coordinate system. This

means that the original circular path is approximated

in a piecewise linear way. Analogously, the orienta-

tion of the camera at each Q

is determined by per-

forming a linear interpolation of the total rotation ma-

trix R

, deﬁned by R

= R

)

−1

, where R

and R

correspond to the rotation parts of Q

and Q

respec-

tively. Therefore, R

is applied in M − 1 steps, which

can be done easily using quaternion notation.

Figure 4: Recovered trajectory from a circular sector of a

robot-driven image acquisition.

The set Q is traversed in order. When the camera

reaches a particular Q

, a signal is send to it in order to

take N pictures in a synchronous way. At any Q

the

ﬁrst picture to be taken corresponds to the calibration

pattern image; then N − 1 pictures of other images

shown on the Wacom Cintiq screen are taken. While

pictures are being taken the robot holds its position.

We used the calibration pattern image to calculate

the extrinsic and intrinsic parameters of the camera,

ANewEvaluationFrameworkandImageDatasetforKeypointExtractionandFeatureDescriptorMatching

255

Figure 5: Some images of exposure varying dataset compound of 15 different images.

and also to estimate the homographies between im-

ages accurately. This also allowed us to rectify the

distortion of the images.

This novel implementation guarantees that the ho-

mography that relate the images taken at Q

and Q

i+1

is the same for all pictures. Thus, this allows to under-

take the performance evaluations under the same ge-

ometric transformation and different image’s texture

patterns.

4.2.1 Image Focus

In addition to the capability of generating unfocused

images with our testing image generator, we also cap-

tured real scenes because unfocused images are not

only Gaussian smoothed versions of a correctly fo-

cused image. The shape of the lens diaphragm and the

value of the lens aperture, which determines depth of

ﬁeld, play an important role in the ﬁnal rendered im-

age; therefore it is not easy to simulate their effect

synthetically. We present an image dataset where the

focus point is progressively varying from a correct fo-

cus point, i.e., all objects in the scene are accurately

rendered in images as sharp, to a point where all ob-

jects appear blurred or unfocused.

In this subset of images, even if the camera was

not moved along the image sequence acquisition,

changes made in the camera focus required to com-

pute the homography between images.

4.3 Photometric Transformations

Photometric transformations are also involved in the

process of image formation. These ones are related

to the camera settings, light conditions and the nature

of the camera hardware (mainly the camera sensor).

Here we present a set of images that show a variation

in the light condition or light exposure, as shown in

Figure 5. The purpose of this subset is to be able to

evaluate the robustness of keypoint extractors repeata-

bility or feature descriptors robustness against illumi-

nation changes and noise.

Image acquisition was carried out by operating the

illumination equipment and the camera remotely, en-

suring that no geometric transformations were applied

and only photometric transformations occur between

the images that form this dataset. This implies that

the homography matrix that relates them geometri-

cally correspond to the identity matrix.

The use of ﬂashes to generate the illumination of

the scene allowed us to vary the amount of light with-

out changing any camera acquisition parameters, set-

ting ﬁxed the aperture value, the exposure time and

ISO speed. In this way, neither the depth of ﬁeld

(DOF) is varied along the images that constitute the

dataset, nor additional noise is added due to an in-

crease of ISO speed or sensor heat because of longer

exposure times. Every image in this dataset is con-

secutively reduced approximately an 1/3 of a f-stop,

starting with a correct exposure in the ﬁrst image.

This dataset is composed of 15 images resulting in

a difference of 4.5 f-stops between the ﬁrst and last

images.

Figure 6: Images from the exposure varying dataset taken

with a mobile device.

Figure 6 shows two images of the same scene

taken with an iPad in controlled illumination condi-

tions. Left image was captured with a correct value

of exposure, while the right image was captured with

approximately 2.5 f-stops less of exposure. For this

setup we used a continuous light source where light

intensity can be set manually. It is worth mention-

ing that the focus point, exposure metering point and

aperture were ﬁxed along the capturing of all images

in the dataset.

As expected, in both scenarios, as the amount of

light decreases, i.e., the signal-to-noise ratio (SNR)

decreases, the amount of digital noise increases. This

is clearly more noticeable in the case of the mobile

device, due to the smaller size of its image sensor,

and therefore a more limited dynamic range compared

with the DSLR camera.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

256

5 IMAGE GENERATOR

In addition to the proposed set of images, we imple-

mented a set of C++ functions and Python scripts that

allow the generation of several testing images by ap-

plying either random or systematic geometric trans-

formations, as well as photometric transformations.

The proposed testing image generator allows to

generate transformed views of a source image by

applying similarity transformations such as isotropic

scaling, as shown in Figure 7, or in-plane rotation, as

well as other afﬁne transformations in one or several

directions.

Digital image noise can be classiﬁed mainly in

two categories, luminance and chrominance. Our im-

age generator is able to create images contaminated

with luminance or chrominance noise, or with both

types simultaneously.

Figure 7: Scale transformed views of the ﬁrst image of

the Grafﬁti dataset proposed in (Mikolajczyk and Schmid,

2002).

6 CONCLUSIONS

We have presented a new set of images, as well as

an image generator and an evaluation framework that

allow evaluating approaches related with image key-

point extraction, description and matching for both

standard and mobile devices. Our framework can be

seen as an evolution of the extensively used evalua-

tion framework of Mikolajczyk and Schmid (Miko-

lajczyk and Schmid, 2002). Moreover, the presented

image dataset has a higher number of images, with

higher resolution and with better controlled geometric

and photometric conditions. The evaluation frame-

work is entirely written in C++, and therefore easily

integrable in many research and development envi-

ronments of this ﬁeld.

We are currently using and extending our pro-

posed framework for the evaluation of state-of-the-art

approaches for keypoint feature descriptors, such as

BRIEF, ORB, RIFF, sGLOH, FREAK, NERIFT, or

BRISK, among others, with real acquired images, as

well as with synthetically generated ones.

REFERENCES

Alahi, A., Ortiz, R., and Vandergheynst, P. (2012). Freak:

Fast retina keypoint. In IEEE Conference on Com-

puter Vision and Pattern Recognition (To Appear).

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. Computer Vision–ECCV

2006, pages 404–417.

Bellavia, F., Tegolo, D., and Trucco, E. (2010). Improv-

ing sift-based descriptors stability to rotations. In Pro-

ceedings of the 2010 20th International Conference on

Pattern Recognition, pages 3460–3463. IEEE Com-

puter Society.

Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-

nal of Software Tools.

Fraundorfer, F. and Bischof, H. (2005). A novel per-

formance evaluation method of local detectors on

non-planar scenes. In Computer Vision and Pat-

tern Recognition-Workshops, 2005. CVPR Work-

shops. IEEE Computer Society Conference on, pages

33–33. IEEE.

Gauglitz, S., H

ollerer, T., and Turk, M. (2011). Evaluation

of interest point detectors and feature descriptors for

visual tracking. International journal of computer vi-

sion, pages 1–26.

Gil, A., Mozos, O., Ballesta, M., and Reinoso, O. (2010). A

comparative evaluation of interest point detectors and

local descriptors for visual slam. Machine Vision and

Applications, 21(6):905–920.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Heikkil

a, M., Pietik

ainen, M., and Schmid, C. (2009). De-

scription of interest regions with local binary patterns.

Pattern recognition, 42(3):425–436.

Hughes, G. and Chraibi, M. (2011). Calculating ellipse

overlap areas. arXiv preprint arXiv:1106.3787.

Leutenegger, S., Chli, M., and Siegwart, R. (2011). Brisk:

Binary robust invariant scalable keypoints. In Com-

puter Vision (ICCV), 2011 IEEE International Con-

ference on, pages 2548–2555. IEEE.

Mikolajczyk, K. and Schmid, C. (2002). An afﬁne invariant

interest point detector. Computer Vision,ECCV 2002,

pages 128–142.

Mikolajczyk, K. and Schmid, C. (2005). A perfor-

mance evaluation of local descriptors. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

27(10):1615–1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., et al. (2007).

Afﬁne covariant features. Collaborative work be-

tween: the Visual Geometry Group, Katholieke Uni-

versiteit Leuven, Inria Rhone-Alpes and the Center for

Machine Perception.

Moreels, P. and Perona, P. (2007). Evaluation of features

detectors and descriptors based on 3d objects. Inter-

national Journal of Computer Vision, 73(3):263–284.

Tuytelaars, T. and Mikolajczyk, K. (2008). Local invariant

feature detectors: a survey. Foundations and Trends



in Computer Graphics and Vision, 3(3):177–280.

ANewEvaluationFrameworkandImageDatasetforKeypointExtractionandFeatureDescriptorMatching

257