Dense Multi-modal Registration with Structural Integrity using

Non-local Gradients

Sheshadri Thiruvenkadam

MIAL, GE Global Research, Bangalore, India

Keywords:

Multi-modal, Non-rigid Registration, Non-local Gradients.

Abstract:

In this work, the challenging problem of dense non-rigid registration [NRR] for multi-modal data is addressed.

We look at a class of differentiable metrics based on weighted L2 distance of non-local image gradients. For

intensity dependent choice of weights, the metric is seen to give enhanced multi-modal capability than using

just gradients. In a variational dense deformation setting, the metric is coupled with non-local regularization

to make the framework feature based. The above combination maintains the visual quality of the registered

image, and gives a good correspondence for features of similar geometry under the challenges of noise, large

motion, and presence of small structures. We also address computational speed ups of the energy minimization

using an approximation scheme. The proposed approach is demonstrated on synthetic and medical data, and

results are quantitatively compared with MI based, diffeomorphic NRR.

1 INTRODUCTION

Multi-modality and large non-rigid motion (relative

to scale of structures) are the primary challenges of

accurate image registration. Mutual information [MI]

based approaches and their extensions have been quite

successful for coarse non-rigid registration of multi-

modal data, see survey (Pluim et al., 2003). Re-

cent works have also extended MI to recover local

deformations (Likar and Pernus, 2001; Hellier and

Barillot, 2000; Loeckx et al., 2010; Lu et al., 2010).

Though MI has been demonstrated and widely used

as a popular multi-modal metric, the non-convexity

of the metric due to interpolation induced artifacts

makes it computationally challenging to use for dense

NRR. The above reason has motivated works to look

at alternative multi-modal metrics that are well be-

haved e.g Normalized gradients (Haber and Moder-

sitzki., 2007). Image gradients have also been widely

addressed in the vision literature e.g. (Lowe, 2004;

Mikolajczyk and Schmid, 2005) for many applica-

tions. Intuitively, match of gradients should give

some multi-modal capability (to spatially linear in-

tensity variations) since differences in relative inten-

sities are only penalized. While the above image gra-

dient based works capture only local intensity inter-

actions, we are motivated to look at non-local inter-

actions between intensities which should give better

robustness to noise and intensity variations. Specif-

Figure 1: Structural integrity and point correspondences.

ically we model intensity differences between pixel

pairs in a large neighborhood through non-local gra-

dients. We wish to note that a recent work (Heinrich

et al., 2011) has also looked at modelling non-local

intensity relationships to achieve promising results on

multi-modal data.

The other challenge of large deformations has

been addressed using multi-resolution strategies, ﬂuid

ﬂow regularization, and diffeomorphic frameworks;

for a recent survey see (Holden, 2008). These

works address the problem of spatial integrity (pre-

serving the topology of structures) under large defor-

mations. Another aspect which has not been carefully

addressed in the registration community is structural

integrity, i.e. the visual quality of the registered im-

age, which is challenged by noise, large motion, and

presence of small structures. To illustrate, in Fig. 1,

the registered T1 MR image (c) looks very similar in

intensity to the ﬁxed image (a), but has lost deﬁnitive

features of the moving image (b). Although it seems

difﬁcult to directly model and subsequently evaluate

the registered image’s visual quality, a key driver is

258

Thiruvenkadam S..

Dense Multi-modal Registration with Structural Integrity using Non-local Gradients.

DOI: 10.5220/0004211702580263

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 258-263

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

the quality of correspondences between key feature

points. Also in many applications such as motion

tracking, it is desirable that the computed map gives

a good correspondence of points of similar geometry.

In Fig. 1 (synthetic example), the registered image

(f) looks exactly like the ﬁxed image (d), but key fea-

ture points (Red ’+’) are incorrectly mapped on the

moving image (e). Feature based methods (Zitova

and Flusser, 2003) as against intensity based meth-

ods have been successful in achieving structural in-

tegrity atleast in neighborhoods of strong features. In

both intensity and feature based methods, the com-

puted maps follow the data near strong feature loca-

tions and are driven to homogeneous regions by local

regularization. As a result, one notices un-realistic

motion in homogeneous regions (e.g. in Fig. 1 (e),

the quality of correspondences are worse in homo-

geneous regions). One way to handle this issue is

through the use of patch based metrics, e.g. (Bruhn

et al., 2005), where the data term is effective in a

neighborhood of strong features as deﬁned by the

patch size. Another possibility is to use non-local reg-

ularization (Sun, 2010; Werlberger, 2010) of the de-

formation ﬁelds which gives increased robustness to

large motion/noise, compared to local approaches.

In this work, we contribute towards a variational

framework capable of dense NRR for Multi-modal

data. The framework also addresses the aspects of

structural integrity of the registered image and qual-

ity of correspondences. A class of differentiable met-

rics based on weighted L2 distance of non-local gradi-

ents is proposed. Intensity dependent weights within

the metric give enhanced multi modal capability sim-

ilar to mutual information based approaches. Since

minimizing the above energy is expensive due to non-

linearities, an approximation scheme for speed up is

proposed. Next, we couple our metric with non-local

regularization (Sun, 2010; Werlberger, 2010) to make

the framework feature based. The above combina-

tion maintains the visual quality of structures in the

registered image and also gives a correspondence of

similar features under challenges of noise, large mo-

tion, and presence of small structures. The approach

is demonstrated using experiments on synthetic and

medical data, and quantitative comparisons are shown

with MI based dense, diffeomorphic NRR.

2 FORMULATION

Given template(ﬁxed) and target(moving) images

f , m : Ω → ℜ, we want to recover transform t between

the image domains. As mentioned previously, the mo-

tivation is to look at intensity-relationships between

Figure 2: Map of level curves of f (Brown), m(Red) before

and after registration

pixel pairs in a larger neighborhood, thus improving

robustness to noise and intensity variations.

2.1 Metric using Non Local Gradients

Although there are many ways to deﬁne intensity-

relationships between pixels, in this work, we want to

preserve intensity differences between mapped pixel

pairs in the template and target domains. Let tx denote

the mapped location for pixel x. We look at a general

class of metrics deﬁned through non-local gradients:

E[t] =

Ω

w(x, y)



(m(ty)− m(tx)) − ( f (y) − f (x))



dydx

(1)

Here w is a weight function that deﬁnes the impor-

tance of the pixel-pair (x,y). For simplicity, assuming

that the weights do not depend on t, we arrive at the

following Euler Lagrange equation [EL] for E. De-

noting ¯w(x, y) =

w(x,y)

Ω

w(x,y) dy

, we have,



Ω

¯w(x, y)m(ty) dy − m(tx) −



Ω

¯w(x, y) f (y) dy − f (x)



∇m(tx) = 0 (2)

The choice of weights impacts multi-modal capa-

bility and computational expense. Obvious choices

of weight functions are w(x, y) = B

(|x − y|), where

is the indicator function for [0, R], and w(x, y) =

(|x − y|), G

is a Gaussian (0, σ). For these weight

functions, it is interesting to see that the descent equa-

tion of (2) is similar to that of SSD-intensity, after

intensity normalization of f and m in local neighbor-

hoods around each pixel. This gives some robustness

to intensity variations. Further, the integrals in (2) are

convolutions and hence fast to compute.

For better multimodal capability, we consider

intensity dependent weights, w(x, y) = δ(| f (x) −

f (y)|)G

(|x − y|), δ is the Dirac delta function. Now

the energy (1) becomes:

E[t] =

Ω

w(x, y)



m(ty) − m(tx)



dydx (3)

DenseMulti-modalRegistrationwithStructuralIntegrityusingNon-localGradients

259

With EL:



Ω

¯w(x, y)m(ty) dy − m(tx)



∇m(tx) = 0 (4)

Intuitively, the metric now maps level curves of f

to level curves of m locally at each pixel x, Fig. 2.

In fact, the descent of (4) would converge when for

each x, the level curve passing through f (x) maps to

a level curve through m(tx). Since the actual intensity

of the iso-contours of f and m is not taken into ac-

count while matching, we get better ﬂexibility to mul-

timodal data as compared to the gaussian choice of

weights. Here, the descent will not involve convolu-

tions, hence approximations for computational speed

up are needed, which would be dealt with shortly.

2.2 Non Local Regularization

In many registration applications, the visual quality of

the registered image and correspondence between fea-

tures that the computed map achieves are important.

Feature based methods (Zitova and Flusser, 2003;

Haber and Modersitzki., 2007) are partly successful

in preserving structure around features and also drive

the registration based on feature correspondence.

The proposed metric (1) is not yet feature based;

e.g. in a monomodal scenario, once the registered im-

age m·t (· denotes composition) matches the ﬁxed im-

age f , the geometry (e.g. gradients, hessian) would

match as well. Analogous to matching image gradi-

ents, we need to match ∇ f (x) and ∇m(tx) for fea-

ture based capability, and not ∇ f (x) and ∇(m · t)(x).

Representing tx = x + u(x), we want to match f (y) −

f (x) with m(y + u(x)) − m(x + u(x)), instead of with

m(y + u(y)) − m(x + u(x)). One possibility would be

to directly use a patch based metric of Non-Local

gradients taking the form

Ω

w(x, y)



m(y + u(x)) −

m(x + u(x)) − ( f (y) − f (x))



dydx. But this would

be expensive even for Gaussian weights, since the EL

would not involve convolutions. Secondly, the above

patch based metric intrinsically assumes rigid mis-

alignments, thus proving very restrictive while recov-

ering non-rigid motion. These issues are highlighted

in the Results section.

With this understanding, to make our energy (1)

feature based, we consider a penalty of the form

Ω

˜w(x, y)|u(y)−u(x)|

dydx with ˜w(x, y) as a weight

function. Adding the above penalty to (1) gives:

reg

[u] =

Ω

w(x, y)



(m(y + u(y)) − m(x + u(x)) − ( f (y) − f (x))



dydx

+λ

reg

Ω

˜w(x, y)|u(y) − u(x)|

dydx (5)

reg

is a parameter balancing the two terms. The

regularization term penalizes non-local gradients of

the deformation ﬁeld and has found recent interests

in optic ﬂow methods. For computational simplic-

ity, we have used a L2 metric for the regularization

term and a straight forward choice for the weight term

˜w(x, y) = G

(|x − y|). Alternatively, the regulariza-

tion term can be replaced with NL-TV and intensity

dependent weights for better results, e.g. (Sun, 2010;

Werlberger, 2010). The distinct advantage over patch

based methods is that the rigidity of matching can be

controlled through λ

reg

thus allowing better capture

of local deformations. Our approach also shows the

beneﬁts of patch based methods namely robustness to

noise, structural integrity, and match of features.

3 NUMERICAL

IMPLEMENTATION

To minimize (5), we use time descent given by the EL

and discretized using explicit ﬁnite differences. For

gaussian weights, the descent equation involves just

convolutions and is fast to compute. When the weight

is intensity dependent for better multimodal capabil-

ity, the integrals in the EL are no longer convolutions

and are expensive to compute. Below, an approxima-

tion scheme for speed up is proposed.

Consider the energy (3) with intensity dependent

weights, and EL given by 4. Using the co-area for-

mula for smooth functions (Jost and Li-Jost, 1998),

assuming |∇ f | > 0 a.e., it can be shown that (4) is

solved by the solutions of

ν(x, f (x))(m(tx) − µ(x, f (x)))∇m(tx) = 0,

where ν(x, λ) =

−1

(λ)

(|x − y|)d ˜s

µ(x, λ) =

−1

(λ)

(|x − y|)m(ty)d ˜s

ν(x, λ)

(6)

Here, d ˜s

|∇ f (x)|

, d ˜s

|∇ f (y)|

, and ds is the arc-

length differential. f

−1

(λ) denotes the level curve

corresponding to λ. We discretize the above equa-

tions with ﬁnite differences and solve using iterative

descent. The descent is analogous to that of the SSD

metric where the update equations seek a transform t

to match intensities of the moving image m and the

evolving ﬁxed image µ. The above arc-length inte-

grals can be reduced to region integrals by working

in a band around the level set λ. Also µ and ν are

’binned’ at discrete locations (x

, λ

) and interpolated

to get the value at (x, λ). Our experiments indicate

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

260

Figure 3: Quality of correspondences of key feature points

(Red ’+’) (a) ﬁxed image (b) Moving image with mapped

points using Approach (c) Registered image using Ap-

proach (d) moving image with mapped points using SSD

NRR (e) Registered image using SSD NRR

that µ and ν have to be updated only once in 10-20 it-

erations effectively making the cost of every iteration

as number of pixels.

4 RESULTS

Here we present results on synthetic and medical data

to illustrate the algorithm’s performance. The use of

non-local gradients for proposed choice of weights

gives computationally tractable dense NRR capability

for multi-modal data. Also, combination with non-

local regularization gives structural integrity of the

registered image (under noise/large motion/presence

of small structures), and gives a good quality of cor-

respondences.

4.1 Quality of Correspondences and

Robustness

In Fig. 3, we illustrate quality of correspondences

using the proposed approach. In the two examples

shown in Fig. 3, the ﬁxed image (a) is registered with

moving image (b). The objective is to see if key fea-

ture points (red ’+’ in (a)) are mapped to respective

locations on the moving image after NRR. In (d), re-

sults from SSD based NRR (SSD intensity metric +

local regularization of motion ﬁelds) shows incorrect

correspondences even in regions where the registered

image (e) is close to the ﬁxed image. Remarkably, our

approach maps points to correct geometric locations

even at homogeneous regions (b), and gives very good

visual quality for the registered image (c). Next, in

Fig. 4, we show capability of preserving small struc-

tures while recovering large motion, and robustness to

noise. In Fig. 4, (a), (b) are noisy, ﬁxed and moving

images (First row: synthetic, Second Row: PET phan-

tom data) with structures of different scales. (c) is the

overlay showing the mismatch, (d) is the result of our

approach. In both examples, the large motion of small

lesion-like structures is corrected under the presence

Figure 4: Quality of registered image with large motion

relative to scale of structures and noise (a) Fixed image

(b) Moving image (c) Overlay showing initial mismatch (d)

Registered image using approach.

Figure 5: Comparison of Approach with Patch SSD (a)

Fixed image (b) Moving image (c) Overlay showing initial

mismatch (d) Registered image using Patch SSD (f) Regis-

tered Result using approach.

Table 1: Timing of Methods.

Method Time (sec)

SSD NRR 27

Patch SSD 232

Approach with Gaussian weights 46

Approach with Intensity based weights 52

of noise. Local NRR approaches would not work here

since there is no overlap of the lesions in the ﬁxed and

moving images, and these methods would collapse

the lesions after NRR. Typical multi-resolution strate-

gies would also not work for large motion of small

structures, since (structure size to motion) ratio would

be preserved across resolutions.

4.2 Comparisons

In subsequent discussion, we compare our approach

with Patch based NRR (e.g. (Bruhn et al., 2005)) and

MI based NRR (e.g. (Lu et al., 2010)):

a) Patch based Methods. Starting with the work of

(Bruhn et al., 2005), there has been a lot of interest in

use of patch based methods within registration mainly

due their robustness to noise and ability to preserve

details of structures under large motion. In this sec-

tion we compare the results of our approach on some

monomodal images with Patch SSD (patch based SSD

metric + local regularization of motion). We wish to

DenseMulti-modalRegistrationwithStructuralIntegrityusingNon-localGradients

261

Figure 6: Synthetic MR comparisons with MI NRR. (a)

Ground truth T1 and T2 images, (b) moving image (c) result

using MI NRR (d) result using approach (e)Error plot (Blue

- before NRR, Cyan - MI NRR, Red - Approach).

comment that the metric used in [Bruhn et al.] is

a linear approximation to the patch based SSD met-

ric, and is suitable for recovering small deformations

only. In spite of the advantages patch based methods

offer, these methods are restrictive in recovering local

non-rigid deformations and are computationally ex-

pensive. Our method shows the advantages of patch

based methods without the above drawbacks. In Fig.

5, in the two examples shown, the ﬁxed image (a) is

non-rigidly deformed to generate the moving image

(b), (c) the overlay showing the mismatch. In (d), we

see that patch SSD has done quite well in recover-

ing deformations under noise. However, artifacts are

seen in the registered image since the metric is too re-

strictive to recover local non-rigid deformations. (e)

shows results using our Approach.

A note on the timing (Table. 1), for the T1 NRR

experiment (250x250 images) in Fig. 5. All runs were

in Matlab, on a 2.6 GHz laptop. It is noted that the

timing for our approach using intensity based weights

is comparable to that with gaussian weights due to

the approximation scheme. The main cost of our ap-

proach over SSD NRR is the use of non-local regular-

ization with a gaussian kernel of width (25x25). Patch

SSD is seen to be expensive since the EL does not in-

volve convolutions and also takes more iterations to

converge under local deformations.

b) Mutual Information [MI] based NRR. There has

been recent interest in extending MI based metrics for

dense NRR. In (Lu et al., 2010), an MI based exten-

sion to diffeomorphic Demon’s algorithm is imple-

mented in a multi-resolution framework [MI NRR].

The main challenge of MI based methods for dense

NRR is that the number of samples available to con-

struct the joint histograms at each point could be

less, resulting in interpolation artifacts. This would

mean optimizing a non-convex metric leading to sub-

optimal solutions, and giving un-realistic deforma-

tions due to over emphasis on regularization.

Now, quantitative comparisons with MI NRR for

MR synthetic data and gated PET-CT data are shown.

In Fig. 6, we consider two experiments, MR T1-T1

NRR and MR T1-T2 NRR. The ﬁrst row shows the

ground truth T1 and T2 images that are well aligned.

We then generated 10 T1(T2) images by applying in-

creasing ranges of random non-rigid motion to the

ground truth T1(T2) images. The 10 T1(T2) images

are then non-rigidly registered to the ground truth T1

image using MI NRR and our approach. A repre-

sentative example is shown in (a)-(c), (a) is the mov-

ing image, (b) is the result using MI NRR, and (c) is

the result using proposed approach. The plot (d) is

the maximum absolute difference error between the

ground truth T1(T2) image and the registered images.

The Blue curve is the error before NRR, the Cyan

curve is error using MI NRR, and the Red curve is

using proposed approach. As clearly indicated in the

error plots and in the examples, the motion recovery

and the quality of the registered images is better using

the proposed approach.

Next, we look at NRR for gated PET-CT. In gated

PET-CT, PET and Cine CT are synchronized across

breathing phases, using e.g. an external tracking de-

vice. The data consisted of 6 cases ( 3 clinical and

3 synthetic PET Phantoms). Each of the data cases

consisted of 6 PET gates (128x128x50), and 6 corre-

sponding in-phase CT gates (512x512x72). We then

picked the central coronal slices for our 2D experi-

ment and brought the CT images to PET resolution.

For each of the 6 data sets, a PET image and its corre-

sponding in-phase CT image were picked as the ref-

erence. Now, the other 5 CT images were non-rigidly

registered to the reference PET image resulting in 30

NRR computations for the 6 data cases. For valida-

tion, the reference CT image is compared with the

registered CT images for each of the data cases.

We illustrate on a clinical case in Fig. 7. Col-

umn (a) shows the PET reference image and the cor-

responding in-phase CT image (ground truth for com-

parison). Column (b) is the registered CT image, Col-

umn (c) is the overlay of the CT image (b) with the

reference PET image, Column (d) is the difference

image of (b) with the reference CT image. The ﬁrst,

second and third rows are the outputs before NRR, us-

ing MI NRR, and using the proposed approach. For

quantitative comparison (Fig. 8), we look at the ab-

solute difference errors between the registered image

and the reference CT image around 10 key landmark

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

262

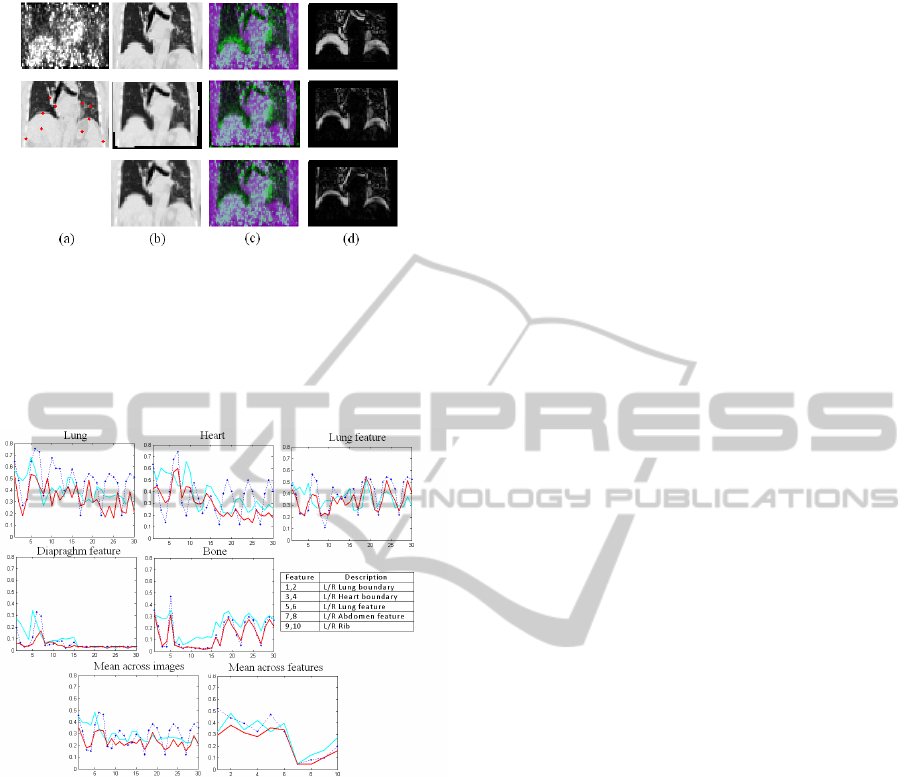
Figure 7: PET CT NRR for a clinical case. Column (a):

PET reference image and the CT reference image with key

landmarks (Red dots), First Row: Before NRR, Second

Row: after MI NRR, Third Row: using proposed approach.

Column (b): registered CT images, Column (c): Overlay of

the CT image (b) with the reference PET image, Column

(d): difference image of (b) with the reference CT image.

Figure 8: First and Second Rows: Error across individual

feature locations (errors due to LEFT/RIGHT feature pairs

have been aggregated for display), Last Row: Mean errors

shown. (Dotted blue - before NRR, Cyan - using MI NRR,

Red - using proposed approach).

locations (red dots shown on the reference CT image

in Fig. 7 (a)). We evaluate the maximum absolute dif-

ference in a 5x5 patch around every landmark point,

for each of the 30 registered images, before NRR (dot-

ted Blue), after MI NRR (Cyan), and after proposed

approach (Red). The errors at different landmark lo-

cations (for display purposes only, the errors due to

left and right landmark pairs are aggregated to save

space) are separately shown. The last row shows the

mean error across images, and across landmark loca-

tions. For the 30 test cases, the proposed approach is

clearly seen to give lesser error values than MI NRR

at key landmark locations.

5 CONCLUSIONS

A weighted L2 match of Non-Local gradients is pro-

posed as a metric for dense multi-modal NRR. The

coupling of NL-regularization gives good correspon-

dence between points of similar geometry in the ﬁxed

and moving images, and preserves the structural in-

tegrity of the registered image. Our method is also

seen to give robustness to noise and ability to preserve

small structures. The approach is demonstrated on

synthetic/medical data, and comparisons are shown

with MI based diffeomorphic NRR.

REFERENCES

Bruhn, A., Weickert, J., and Schnrr, C. (2005). Lu-

cas/kanade meets horn/schunck: Combining local and

global optic ﬂow methods. International Journal of

Computer Vision, 61:211–231.

Haber, E. and Modersitzki., J. (2007). Intensity gradient

based registration and fusion of multimodal images.

methods of information in medicine. Methods of in-

formation in medicine, 46(3):292–299.

Heinrich, M. P., Jenkinson, M., and et al. (2011). Non-

local shape descriptor: a new similarity metric for

deformable multi-modal registration. MICCAI’11,

pages 541–548.

Hellier, P. and Barillot, C. (2000). Multimodal non-rigid

warping for correction of distortions in functional mri.

MICCAI, pages 512–520.

Holden, M. (2008). A review of geometric transformations

fornonrigid body registration. IEEE Transactions on

Medical Imaging, 27(1).

Jost, J. and Li-Jost, X. (1998). Calculus of variations. Cam-

bridge Univ. Press.

Likar, B. and Pernus, F. (2001). A hierarchical approach to

elastic registration based on mutual information. Im-

age Vision Comput., 19(1-2):33–44.

Loeckx, D., Slagmolen, P., Maes, F., Vandermeulen, D., and

Suetens, P. (2010). Nonrigid image registration using

conditional mutual information. IEEE Transactions

on Medical Imaging, 29(1).

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. Int. J. Comput. Vision, 60(2).

Lu, H., Reyes, M., and et al. (2010). Multi-modal diffeo-

morphic demons registration based on point-wise mu-

tual information. ISBI, 27(1).

Mikolajczyk, K. and Schmid, C. (2005). A perfor-

mance evaluation of local descriptors. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

27(10):1615–1630.

Pluim, J. P. W., Maintz, J. B. A., and Viergever, M. A.

(2003). Mutual information based registration of med-

ical images: A survey. IEEE Trans. Med. Imaging,

22(8):986–1004.

Sun (2010). Secrets of optical ﬂow estimation and their

principles. CVPR, 12(1):234–778.

Werlberger (2010). Motion estimation with non-local total

variation regularization. CVPR, 13(1):234–778.

Zitova, B. and Flusser, J. (2003). Image registration meth-

ods:a survey. Image Vision Comput., 21(11):977–

1000.

DenseMulti-modalRegistrationwithStructuralIntegrityusingNon-localGradients

263