
Image Guided Cost Aggregation for Hierarchical Depth Map Fusion
Thilo Borgmann and Thomas Sikora
Communication Systems Group, Technische Universit
¨
at Berlin, Berlin, Germany
Keywords:
Multi View Stereo, Stereo Matching, Depth Estimation, Depth Map Fusion.
Abstract:
Estimating depth from a video sequence is still a challenging task in computer vision with numerous applica-
tions. Like other authors we utilize two major concepts developed in this field to achieve that task which are
the hierarchical estimation of depth within an image pyramid as well as the fusion of depth maps from different
views. We compare the application of various local matching methods within such a combined approach and
can show the relative performance of local image guided methods in contrast to commonly used fixed–window
aggregation. Since efficient implementations of these image guided methods exist and the available hardware
is rapidly enhanced, the disadvantage of their more complex but also parallel computation vanishes and they
will become feasible for more applications.
1 INTRODUCTION
Reconstructing a three–dimensional representation of
a scene from multiple images of a video sequence
is one of the most important topics in computer vi-
sion. It serves as an essential basis for numerous ap-
plication from different areas like robotics, medical
imaging, video processing and many more. Intense
research on this topic has been done for many years
and the state–of–the–art advances rapidly. Yet it is
still a challenging task to acquire high–quality 3D re-
constructions using image–based methods only.
The enormous amount of algorithms proposed to
accomplish this task use a wide variety of approaches.
The most important property to distinguish between
these algorithms is their scope of matching and opti-
mization, either locally or globally. This categoriza-
tion holds in general, even though there are some ap-
proaches in between. Algorithms utilizing a global
optimization tend to produce the most accurate re-
sults. Unfortunately, achieving this quality usually re-
quires complex computations and is therefore not al-
ways feasible with respect to the desired application.
Also, these algorithms usually provide limited capa-
bilities of parallelization. Thus even modern com-
puter hardware cannot compensate this drawback due
to their still limited computation of sequential parts of
these algorithms.
In contrast to these methods, algorithms based on
local matching approaches are much less complex and
offer the advantage of rapid computation. Although
they usually suffer from the ambiguities within their
local scope. Early approaches show a severe differ-
ence in quality compared to their globally optimized
counterparts. However, recent improvements to local
matching can significantly reduce the gap between the
two categories. Always considering a limited local
area only, these methods also offer excellent possibil-
ities for parallelization. Modern computer hardware
in turn provide a basis for such massive parallel com-
putation so that the number of high–quality real–time
capable algorithms permanently increase.
For a comprehensive overview of existing meth-
ods and their relative performance evaluation, we re-
fer to the publicly available benchmarks covering this
topic (Scharstein et al., 2001) (Seitz et al., 2006)
(Strecha et al., 2008).
Nevertheless, there is always the trade–off be-
tween quality and computational complexity. Given
a set of calibrated images from a video sequence,
we utilize two major concepts developed in this area,
which are the hierarchical estimation of depth maps
(Yang and Pollefeys, 2003) (Zach et al., 2004) (Cor-
nelis and Van Gool, 2005) (Nalpantidis et al., 2009)
and the fusion of depth maps from multiple views
(Zitnick et al., 2004) (Merrell et al., 2007) (Zach,
2008) (Zhang et al., 2009) (Unger et al., 2010).
The fusion of the depth maps allows to achieve
a high quality while the hierarchical structure of the
depth estimation helps to reduce complexity. We are
not the first to combine these approaches (McKinnon
et al., 2012). The authors evaluated the influence of
199
Borgmann T. and Sikora T..
Image Guided Cost Aggregation for Hierarchical Depth Map Fusion.
DOI: 10.5220/0004212901990207
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 199-207
ISBN: 978-989-8565-48-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

several parameters to their approach but the choice
of the initial depth map estimation and cost aggre-
gation is just roughly covered. The several authors
of the former contributions about hierarchical estima-
tion and depth map fusion do also not report compara-
tively about different estimation approaches. Thus, in
contrast to other methods, our contribution is to reveal
the relative performance of the applied cost aggrega-
tion used throughout the hierarchical estimation pro-
cess instead of focusing on a sophisticated process-
ing on or between the higher levels of the approach.
Although a global matching algorithm seems feasible
at that stage of the hierarchical processing, the rel-
ative overhead remains and we stick to local meth-
ods. We therefore implemented and compared the
performance of several well–known cost aggregation
methods that have already been proven their ability to
achieve high-quality estimation results as well as be-
ing computational efficient. We integrate them into a
rather simple hierarchical scheme for the applied cost
aggregation to be the dominant factor within this pro-
cess. This leads us to the relative performance of the
initial depth map and cost aggregation used in such a
hierarchical framework.
2 RELATED WORK
Common two–view disparity estimation algorithms
compute separate disparity maps for each of the
two views, postprocessed by a left–right consistency
check. By applying that, ambiguous matches and oc-
cluded pixels are detected. This approach has also
been transfered and adapted for depth estimation in
multi–view matching (Zitnick et al., 2004) (Merrell
et al., 2007).
Hierarchical disparity matching is also a common
approach in the field of stereo matching. In (Yang
and Pollefeys, 2003) (Zach et al., 2004) (Cornelis and
Van Gool, 2005) the authors successfully demonstrate
the real–time capabilities and efficiency of their ap-
proaches.
A combination of the former methods is pre-
sented in (McKinnon et al., 2012). The authors
describe an iterative approach of the fusion of
depth maps throughout their hierarchical estimation
scheme. Within each level of the hierarchy, the depth
map is further refined by an iterative application of
the connectivity constraint (Cornelis and Van Gool,
2005).
Many cost aggregation methods have been pro-
posed based on variable support regions (Tombari
et al., 2008a). Among many that dynamically select
different or multiple support windows (Hirschm
¨
uller
et al., 2002) or varying window sizes (Veksler, 2003),
we concentrate on those approaches that define the
support region based on the local surrounding within
the image like (Yoon and Kweon, 2006) (Tombari
et al., 2008b) (Zhang et al., 2009) (He et al., 2010).
We refer to these as image guided aggregation meth-
ods.
Cost aggregation methods are amongst the most
important things to consider for stereo matching algo-
rithms. According to the rapid development of these
algorithms, cost aggregation methods are also rapidly
enhanced. Next to benchmarks like (Scharstein et al.,
2001) (Strecha et al., 2008), which evaluate complete
algorithms, the bare cost initialization and aggrega-
tion methods have also been addressed by other con-
tributions.
In (Wang et al., 2006) the authors evaluate a set
of well–known cost initialization methods in combi-
nation with image guided and unguided cost aggrega-
tions. They use several sequences from the Middle-
burry stereo data set to compare the resulting dispar-
ity estimations. All methods are evaluated by being
incorporated into the same disparity estimator. Con-
cerning the evaluated image guided cost aggregation
methods they approve the expected gain in quality of
the disparity estimation. They also show the increas-
ing complexity when using these methods.
A very comprehensive evaluation of cost initial-
izations and cost aggregations as well as their rela-
tion to each other has been done in (Tombari et al.,
2008a). Many different image guided aggregation
methods have been evaluated also using the Middle-
burry stereo data set. They use a simplistic winner–
takes–all approach to generate their results for a clear
dependency on the incorporated initialization and ag-
gregation methods. We instead do not only cover the
quality of the generated depth map but also the in-
fluence of repeatedly applied depth map fusion and
refinement using the corresponding cost and aggrega-
tion methods.
3 HIERARCHICAL ALGORITHM
For our hierarchical implementation, we adopt several
techniques from previous approaches of (Cornelis and
Van Gool, 2005) and (McKinnon et al., 2012).
We iterate through an image pyramid. Each level
k of the pyramid holds frames of half the width and
height of the size of the succeeding level. In this im-
plementation, we reduce the resolution for the lowest
level of the pyramid to 1 / 64th of the full resolution.
Due to our hardware limitations, we have to restrict
the highest level of the pyramid to 1 / 4th of the full
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
200

resolution (1536x1024 pixels).
For the first level k = 0 of this hierarchy, we ap-
ply an initial plane–sweep based estimation. For each
succeeding level k > 0, we apply a refining depth map
based sweep adopted from (Cornelis and Van Gool,
2005). The depth estimates of the current level are
then processed by a depth map fusion before the algo-
rithm proceeds to the next level in the hierarchy. For
that, all depth estimates of the current level have to
be concurrently computed. After the first level k = 0
has been processed, the parameters r
k
and d
k
that in-
fluence the refining depth map sweep used in all lev-
els k > 0 are updated according to the current level.
This hierarchical approach can be seen as a simpli-
fied variant of the scheme presented in (McKinnon
et al., 2012) with just one refinement iteration within
the levels of the hierarchy.
The following pseudo code outlines the described
algorithm:
For all lev els k
For all ca m er as
If k = 0 then
Ini ti a l Dep t h E s ti ma ti on
Else
r
k
= k * r
0
d
k
= 1/2 * d
k−1
Dept h Map Swe ep
Fi
Dept h Map Fu sio n
End
End
In the following sections we briefly outline each
individual step and describe the influence of the pa-
rameters r
k
and d
k
.
3.1 Initial Depth Estimation
For each camera, we basically apply a fronto–parallel
plane–sweep approach (Collins, 1996). We divide
the sequence into two halves for the preceding and
succeeding views according to (Kang et al., 2001).
The number of views projected onto the sweep–
plane might vary, but we found using one view to
be sufficient. The sweep–plane is then projected into
the reference camera and for each depth the photo–
consistency function according to the applied cost and
aggregation methods is computed.
Throughout all depths we apply a simple winner–
takes–all approach to receive the minimal cost for
each pixel. A simple parabolic interpolation is applied
using the depth and cost values of the sweep–layers in
front and behind the minimum plane to achieve a con-
tinuous depth value.
A second sweep follows with the projecting view
used as the reference view to apply a standard
left–right consistency check to remove ambiguous
matches. This bidirectional sweeping procedure is ap-
plied using the preceding as well as the succeeding
views. The combination of both intermediate depth
maps D
i,L
, D
i,R
results in a continuous depth map
for each reference view D
i
= D
i,L
S
D
i,R
. Note that
one of these bidirectional sweeps can be reused for
the depth map estimation of the succeeding reference
view: D
i−1,R
= D
i,L
. Thus, for each camera pair of the
sequence just one bidirectional sweep has to be com-
puted. The initial depth estimation is followed by the
first depth map fusion that is equal to all levels.
3.2 Depth Map Sweep
The fused depth maps from the previous level k − 1
are swept again using the current resolution within a
small range d
k
around the current depth estimate (Cor-
nelis and Van Gool, 2005). This range around the esti-
mate is decreased to half the size of the previous level:
d
k
=
1
2
d
k−1
(1)
The respective window or kernel sizes s depend on
a given parameter r
k
, so that s = (2r
k
+ 1)
2
. For the
cross–based method of (Zhang et al., 2009), r
k
defines
the maximum arm length used. The value of r
k
is
linearly increased by the current level on basis of the
initial size:
r
k
= kr
0
(2)
For the image guided aggregation methods, a sec-
ond parameter e is required that controls the image
guided creation of the support region. This parame-
ter is fixed for all applications of the corresponding
aggregation but differs according to the method used.
However, for our simplified hierarchical approach we
rely on the refined sampling interval and the enforced
smoothness during the fusion stage to enhance the es-
timation and do not incorporate a connectivity con-
straint.
3.3 Depth Map Fusion
In this stage the depth maps of the surrounding views
generated in the same level are projected into the ref-
erence view. We apply only two simple validations to
reject outliers from being candidates for the fusion.
First, we accept only candidates that are within a
close distance ε to the reference estimation and there-
fore support its location (Merrell et al., 2007). Sec-
ond, the euclidean distance between the color vectors
of the reference pixel and the candidate pixel is tested
to be within another threshold θ. From the set of re-
maining candidates, we apply another winner–takes–
ImageGuidedCostAggregationforHierarchicalDepthMapFusion
201
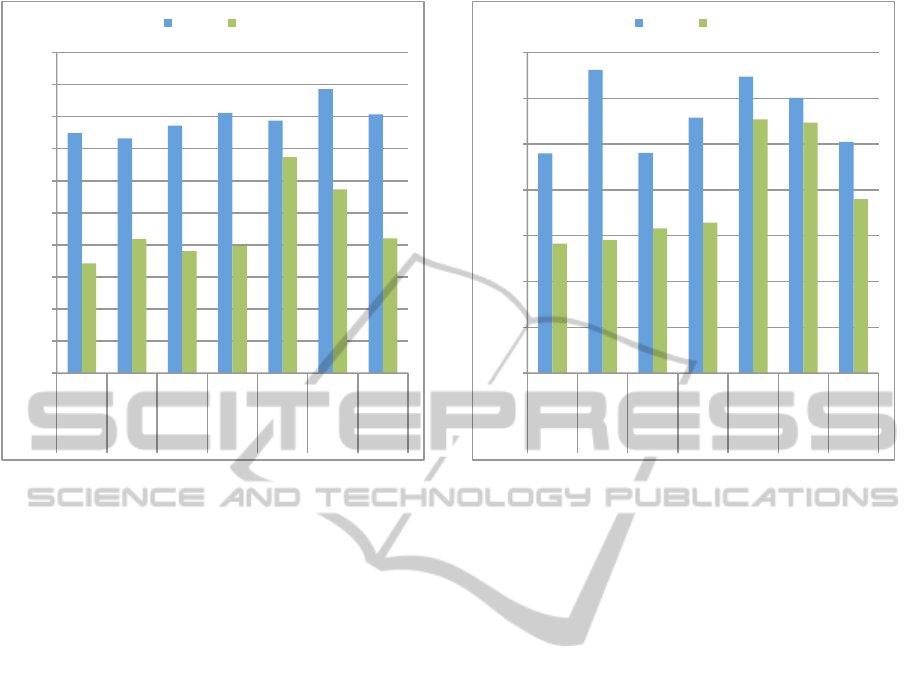
0%#
5%#
10%#
15%#
20%#
25%#
30%#
35%#
40%#
45%#
50%#
ADC#
OPT#
ADC#
OPT#
SAD#
SSD#
NCC#
CB#
CB#
GF#
GF#
Level#0#
Final#
Figure 1: Comparison of the fusion results of all combina-
tions using their respective best performing parameters for
‘Fountain’.
all approach to select the candidate with the smallest
cost value corresponding to its origin view.
The last step is to apply a mean filter to smooth
the fused depth maps. To preserve depth discontinu-
ities, we compute this filter within a cross–based sup-
port region generated by (Zhang et al., 2009) using
a small maximum arm length r
f
. The used parame-
ters θ, ε and r
f
are constant for all levels. The fused
depth maps are then passed to the next iteration on the
succeeding level.
4 EVALUATION
We compare several approaches for cost initializa-
tion and cost aggregation used to compute the photo–
consistency function during the plane-sweeps.
Some of the most common combinations are the
absolute intensity differences and the squared inten-
sity differences, aggregated within a fixed–window
to form the well–known sum of absolute differences
(SAD) and sum of squared differences (SSD) cost
functions. Next to these, there is also the normalized
cross–correlation (NCC) to be considered in this cat-
egory.
For the comparison with image guided cost func-
tions, we have chosen two state–of–the–art ap-
proaches. The first is the guided image filtering (GF)
approach presented in (He et al., 2010). The second is
the cross–based aggregation method (CB) of (Zhang
0%#
10%#
20%#
30%#
40%#
50%#
60%#
70%#
ADC#
OPT#
ADC#
OPT#
SAD#
SSD#
NCC#
CB#
CB#
GF#
GF#
Level#0#
Final#
Figure 2: Comparison of the fusion results of all combina-
tions using their respective best performing parameters for
‘Herz–Jesu’.
et al., 2009). Among many alternatives to these ag-
gregation methods, these two have proven to perform
very accurately in state–of–the–art stereo matching
algorithms (Rhemann et al., 2011) (Mei et al., 2011)
and also provide very efficient implementations using
integral images (Crow, 1984). In (Mei et al., 2011) the
cross–based aggregation is applied to a cost initializa-
tion based on a linear combination of the absolute dif-
ferences and the census transform called AD–Census
(ADC). In (Rhemann et al., 2011) a common cost ini-
tialization based on the absolute differences and gra-
dients (OPT) is used, well–known from many contri-
butions concerning the optical flow computation.
Therefore we include in our comparison both
these combinations (CB + ADC, GF + OPT) as well
as the combination of exchanged initialization and ag-
gregation methods (CB + OPT, GF + ADC). Thus, we
have a set of seven combinations to be evaluated in
our hierarchical framework.
We have chosen two well–known wide–baseline
outdoor sequences from the data set provided by
(Strecha et al., 2008) for our evaluation: ‘Fountain’
and ‘Herz-Jesu’. These sequences feature a ground–
truth 3D–model, acquired using a laser range scanner,
and ground-truth camera calibration. We measure the
quality of our results by projecting the ground–truth
model into all processed cameras of the sequence. For
each pixel the resulting depth value of that projection
is then compared to the depth values generated by our
hierarchical algorithm. We generate a histogram of
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
202
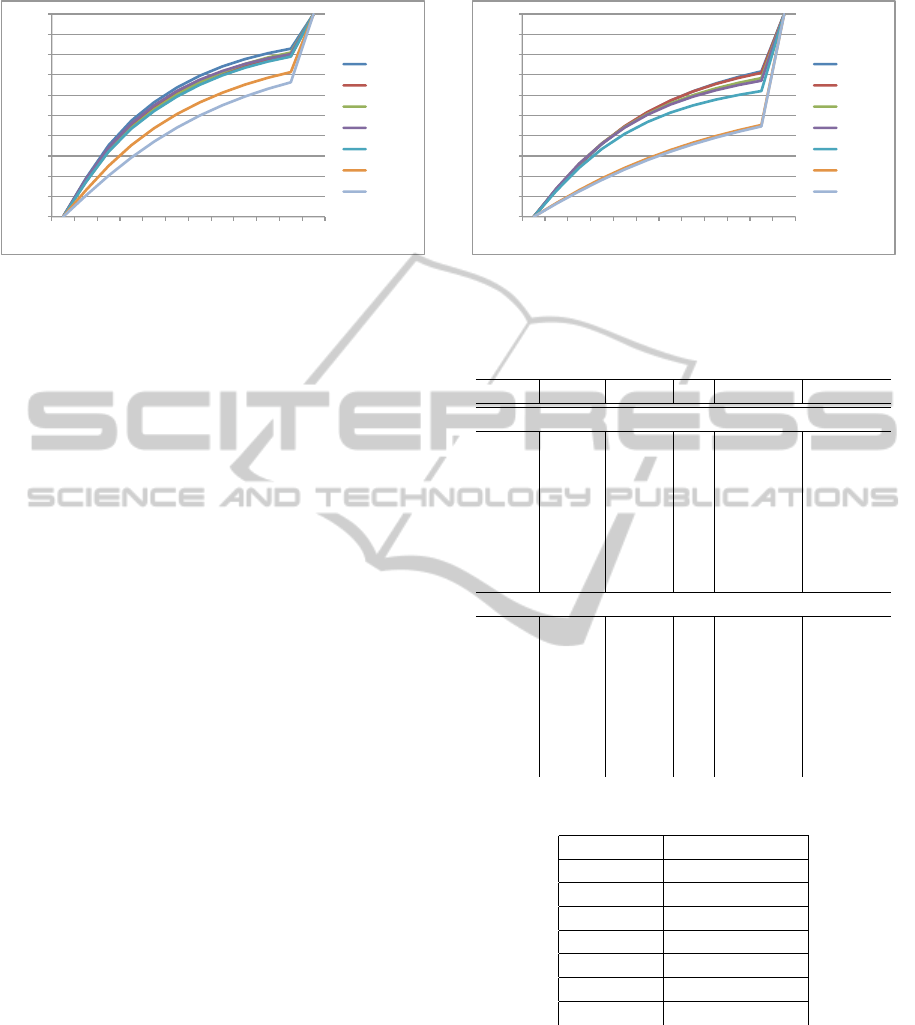
0%#
10%#
20%#
30%#
40%#
50%#
60%#
70%#
80%#
90%#
100%#
0#
1#
2#
3#
4#
5#
6#
7#
8#
9#
10#
11#
CB#+#ADC#
CB#+#OPT#
GF#+#ADC#
GF#+#OPT#
NCC#
SSD#
SAD#
Figure 3: Cumulative distribution of best performing com-
binations for sequence ‘Fountain’.
eleven bins to accumulate pixels according to their
depth difference. Like (McKinnon et al., 2012), we
define a threshold σ equivalent to 3mm for each bin of
the histogram. All estimates with a difference greater
than 10σ as well as all missing pixels according to
the ground–truth are accumulated in the last bin. This
histogram is closely related to the evaluation scheme
used in (Strecha et al., 2008) and (McKinnon et al.,
2012). It reveals the precision of the estimated pix-
els as well as the completeness in terms of the given
threshold of 10σ.
We compare the various combinations of cost and
aggregation methods primarily by their amount of
precisely estimated pixels. For that we can utilize
the last bin of the histogram. The lower that value
the more pixels have been estimated with a sufficient
precision and the better the aggregation method per-
forms. The values presented are given by percentage
of all pixels estimated. In figure 1 and figure 2 we
compare the best performing parameters for all seven
combinations applied to the according sequence. For
each combination, the result after the first depth map
fusion at level k = 0 and the result of the final depth
map fusion are shown. This illustrates the overall per-
formance as well as the benefits of the hierarchical
processing. The corresponding parameters are given
in table 1. In figure 3 and figure 4 we show the ac-
cording cumulative distribution to visualize the rel-
ative precision for these combinations, too. For the
best and worst performing image guided and fixed
methods, we show the color–coded differences to the
ground-truth for a subimage of both sequences in fig-
ure 5. The pixel–wise differences are color–coded ac-
cording to bins of the corresponding histogram, from
white for small differences less or equal to σ to black
for differences up to 10σ. All blue pixels represent
differences of more than 10σ.
We use the parameters given in table 2 for the
complete evaluation. The parameters r
0
and e in-
fluence the behavior of the aggregation methods and
0%#
10%#
20%#
30%#
40%#
50%#
60%#
70%#
80%#
90%#
100%#
0#
1#
2#
3#
4#
5#
6#
7#
8#
9#
10#
11#
CB#+#ADC#
CB#+#OPT#
GF#+#ADC#
GF#+#OPT#
NCC#
SSD#
SAD#
Figure 4: Cumulative distribution of best performing com-
binations for sequence ‘Herz–Jesu’.
Table 1: Best performing parameter values for each combi-
nation and sequence.
Agg. Cost e r
0
Level 0 Final
Fountain:
CB ADC 12 3 37,4383 17,1133
CB OPT 12 3 36,6367 20,8848
GF ADC 0,001 1 38,6234 19,0225
GF OPT 0,001 2 40,5867 19,8058
SAD 1 39,3672 33,6869
SSD 2 44,3056 28,6606
NCC 2 40,3505 21,0151
Herz–Jesu:
CB ADC 5 1 48,0009 28,2878
CB OPT 5 2 66,2230 29,0251
GF ADC 0,100 1 48,0823 31,6208
GF OPT 0,100 1 55,7852 32,8818
SAD 1 64,7667 55,4109
SSD 2 60,1193 54,7170
NCC 1 50,4895 37,9934
Table 2: Parameter values used for the parameter-sweep.
Parameter Value(s)
θ 0.2
r
f
r
0
d
1
0.3
ε 0.1
r
0
1, 2, 3, 4, 6
e(GF) 0.1,0.01, 0.001
e(CB) 5, 8, 12
are therefore assigned several values for a parameter–
sweep. Note that e depends on the image guided
method and has completely different values assigned.
For the guided image filter (He et al., 2010), this value
is similar to ε of the original implementation. For
the cross–based aggregation (Zhang et al., 2009), this
value corresponds to τ.
ImageGuidedCostAggregationforHierarchicalDepthMapFusion
203

(a) CB + ADC (b) GF + OPT (c) NCC (d) SAD
Figure 5: Subimages of both sequences showing the pixel–wise evaluation by color–coded differences to the ground–truth.
Differences range from ≤ 1σ (white) to ≤ 10σ (black). Blue color indicates a difference of > 10σ. Sequence ‘Fountain’
is shown in the upper row, sequence ‘Herz–Jesu’ is shown in the lower row. The best (a) and the worst (b) image guided
combinations as well as the best (c) and the worst (d) fixed methods are shown.
5 CONCLUSIONS
We can show in our evaluation that the applica-
tion of image guided methods generally produce a
more complete and precise result, see figures 1, 2,
3, 4 and 5. For the ‘Fountain’ sequence, the differ-
ence between the best performing image guided and
non–guided method is around 4%, and almost 10%
for ‘Herz–Jesu’. Although the normalized cross–
correlation performs almost as well as the image
guided approach (GF + OPT) on the ‘Fountain’ se-
quence, the difference becomes larger in a more
complex sequence like ‘Herz–Jesu’. Nevertheless, it
clearly outperforms the SAD and SSD approaches on
both sequences.
Thus, the application of image guided methods
has its benefits although they require a slightly more
complex computation. However, this disadvantage
vanishes due to the improving hardware capabili-
ties in terms of parallel computing. The normalized
cross–correlation offers a good trade–off between
quality and complexity for both sequences. These re-
sults encourage us to further investigate the applica-
tion of image guided methods in a more sophisticated
hierarchical estimation approach.
ACKNOWLEDGEMENTS
The authors like to thank David M
c
Kinnon, Ryan
Smith and Ben Upcroft for their most valuable sup-
port of various data and personal contact.
REFERENCES
Collins, R. (1996). A space-sweep approach to true
multi-image matching. In Computer Vision and Pat-
tern Recognition, 1996. Proceedings CVPR’96, 1996
IEEE Computer Society Conference on, pages 358–
363. IEEE.
Cornelis, N. and Van Gool, L. (2005). Real-time connec-
tivity constrained depth map computation using pro-
grammable graphics hardware. In Computer Vision
and Pattern Recognition, 2005. CVPR 2005. IEEE
Computer Society Conference on, volume 1, pages
1099–1104. IEEE.
Crow, F. (1984). Summed-area tables for texture mapping.
ACM SIGGRAPH Computer Graphics, 18(3):207–
212.
He, K., Sun, J., and Tang, X. (2010). Guided image filtering.
Computer Vision–ECCV 2010, pages 1–14.
Hirschm
¨
uller, H., Innocent, P., and Garibaldi, J. (2002).
Real-time correlation-based stereo vision with re-
duced border errors. International Journal of Com-
puter Vision, 47(1):229–246.
Kang, S., Szeliski, R., and Chai, J. (2001). Handling occlu-
sions in dense multi-view stereo. In Computer Vision
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
204

and Pattern Recognition, 2001. CVPR 2001. Proceed-
ings of the 2001 IEEE Computer Society Conference
on, volume 1, pages I–103. IEEE.
McKinnon, D., Smith, R., and Upcroft, B. (2012). A semi-
local method for iterative depth-map refinement. In
Proceedings of the IEEE International Conference on
Robotics and Automation (ICRA 2012). IEEE.
Mei, X., Sun, X., Zhou, M., Jiao, S., Wang, H., and Zhang,
X. (2011). On building an accurate stereo matching
system on graphics hardware. In Computer Vision
Workshops (ICCV Workshops), 2011 IEEE Interna-
tional Conference on, pages 467–474. IEEE.
Merrell, P., Akbarzadeh, A., Wang, L., Mordohai, P.,
Frahm, J., Yang, R., Nist
´
er, D., and Pollefeys, M.
(2007). Real-time visibility-based fusion of depth
maps. In Computer Vision, 2007. ICCV 2007. IEEE
11th International Conference on, pages 1–8. Ieee.
Nalpantidis, L., Amanatiadis, A., Sirakoulis, G., Kyriak-
oulis, N., and Gasteratos, A. (2009). Dense dispar-
ity estimation using a hierarchical matching technique
from uncalibrated stereo vision. In Imaging Systems
and Techniques, 2009. IST ’09. IEEE International
Workshop on, pages 427 –431.
Rhemann, C., Hosni, A., Bleyer, M., Rother, C., and
Gelautz, M. (2011). Fast cost-volume filtering for vi-
sual correspondence and beyond. In Computer Vision
and Pattern Recognition (CVPR), 2011 IEEE Confer-
ence on, pages 3017–3024. IEEE.
Scharstein, D., Szeliski, R., and Zabih, R. (2001). A tax-
onomy and evaluation of dense two-frame stereo cor-
respondence algorithms. In Stereo and Multi-Baseline
Vision, 2001. (SMBV 2001). Proceedings. IEEE Work-
shop on, pages 131 –140.
Seitz, S., Curless, B., Diebel, J., Scharstein, D., and
Szeliski, R. (2006). A comparison and evaluation
of multi-view stereo reconstruction algorithms. In
Computer Vision and Pattern Recognition, 2006 IEEE
Computer Society Conference on, volume 1, pages
519 – 528.
Strecha, C., von Hansen, W., Van Gool, L., Fua, P., and
Thoennessen, U. (2008). On benchmarking camera
calibration and multi-view stereo for high resolution
imagery. In Computer Vision and Pattern Recognition,
2008. CVPR 2008. IEEE Conference on, pages 1 –8.
Tombari, F., Mattoccia, S., Di Stefano, L., and Addimanda,
E. (2008a). Classification and evaluation of cost ag-
gregation methods for stereo correspondence. In Com-
puter Vision and Pattern Recognition, 2008. CVPR
2008. IEEE Conference on, pages 1–8. IEEE.
Tombari, F., Mattoccia, S., Di Stefano, L., and Addimanda,
E. (2008b). Near real-time stereo based on effective
cost aggregation. In Pattern Recognition, 2008. ICPR
2008. 19th International Conference on, pages 1–4.
IEEE.
Unger, C., Wahl, E., Sturm, P., Ilic, S., et al. (2010). Prob-
abilistic disparity fusion for real-time motion-stereo.
Citeseer.
Veksler, O. (2003). Fast variable window for stereo corre-
spondence using integral images. In Computer Vision
and Pattern Recognition, 2003. Proceedings. 2003
IEEE Computer Society Conference on, volume 1,
pages I–556. IEEE.
Wang, L., Gong, M., Gong, M., and Yang, R. (2006). How
far can we go with local optimization in real-time
stereo matching. In 3D Data Processing, Visualiza-
tion, and Transmission, Third International Sympo-
sium on, pages 129–136. IEEE.
Yang, R. and Pollefeys, M. (2003). Multi-resolution real-
time stereo on commodity graphics hardware. In
Computer Vision and Pattern Recognition, 2003. Pro-
ceedings. 2003 IEEE Computer Society Conference
on, volume 1, pages I–211. IEEE.
Yoon, K. and Kweon, I. (2006). Adaptive support-weight
approach for correspondence search. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
28(4):650–656.
Zach, C. (2008). Fast and high quality fusion of depth
maps. In Proceedings of the International Symposium
on 3D Data Processing, Visualization and Transmis-
sion (3DPVT), volume 1.
Zach, C., Karner, K., and Bischof, H. (2004). Hierarchi-
cal disparity estimation with programmable 3d hard-
ware. In Proc. of WSCG, Pilsen, Czech Republic,
pages 275–282.
Zhang, G., Jia, J., Wong, T., and Bao, H. (2009). Consis-
tent depth maps recovery from a video sequence. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 31(6):974–988.
Zitnick, C., Kang, S., Uyttendaele, M., Winder, S., and
Szeliski, R. (2004). High-quality video view interpo-
lation using a layered representation. In ACM Trans-
actions on Graphics (TOG), volume 23, pages 600–
608. ACM.
APPENDIX
The complete evaluation data is given in separate ta-
bles. There are two tables for each sequence, one for
fixed–window and one for image guided aggregation,
respectively. Tables 3 and 5 show the results for the
sequence ‘Fountain’ and tables 4 and 6 show the re-
sults for the sequence ‘Herz–Jesu’. The values given
in the columns ‘Level 0’ and ‘Final’ are the percent-
ages of pixels estimated with an insufficient precision
after the first and final depth map fusion, respectively.
ImageGuidedCostAggregationforHierarchicalDepthMapFusion
205

Table 3: Parameter–sweep of image guided aggregation for
the ‘Fountain’ sequence.
Agg. Cost e r
0
Level 0 Final
CB ADC 5 1 37,7922 21,3303
CB ADC 5 2 39,6136 20,5099
CB ADC 5 3 38,6625 19,3956
CB ADC 5 4 39,418 19,5801
CB ADC 5 6 39,617 17,6259
CB ADC 8 1 37,6795 21,4545
CB ADC 8 2 39,5631 19,9244
CB ADC 8 3 38,295 18,7349
CB ADC 8 4 39,2334 17,7528
CB ADC 8 6 40,1979 18,2764
CB ADC 12 1 37,4367 18,4192
CB ADC 12 2 39,2775 17,5535
CB ADC 12 3 37,4383 17,1133
CB ADC 12 4 39,6574 18,3329
CB ADC 12 6 41,2455 19,3537
CB OPT 5 1 40,0748 25,8658
CB OPT 5 2 38,81 22,9363
CB OPT 5 3 37,6746 21,7772
CB OPT 5 4 38,2792 22,32
CB OPT 5 6 38,0735 20,92
CB OPT 8 1 40,7023 25,9492
CB OPT 8 2 38,2409 21,7358
CB OPT 8 3 37,1505 21,1068
CB OPT 8 4 37,797 21,4484
CB OPT 8 6 39,1751 20,9398
CB OPT 12 1 41,4982 25,3186
CB OPT 12 2 37,9567 21,3778
CB OPT 12 3 36,6367 20,8848
CB OPT 12 4 38,15 21,4235
CB OPT 12 6 40,157 21,5007
GF ADC 0,100 1 40,3396 19,2574
GF ADC 0,100 2 41,895 21,2373
GF ADC 0,100 3 43,4714 24,6391
GF ADC 0,100 4 45,3187 27,7024
GF ADC 0,100 6 49,313 34,1429
GF ADC 0,010 1 39,8775 19,0698
GF ADC 0,010 2 41,4333 20,5663
GF ADC 0,010 3 42,659 23,2175
GF ADC 0,010 4 44,3367 25,9867
GF ADC 0,010 6 48,1713 31,8384
GF ADC 0,001 1 38,6234 19,0225
GF ADC 0,001 2 40,3896 19,2996
GF ADC 0,001 3 41,9276 21,7289
GF ADC 0,001 4 43,5808 24,1429
GF ADC 0,001 6 46,6741 28,7754
GF OPT 0,100 1 38,567 19,9531
GF OPT 0,100 2 43,6802 20,5242
GF OPT 0,100 3 45,5161 32,7966
GF OPT 0,100 4 47,1033 26,9157
GF OPT 0,100 6 50,8852 33,962
GF OPT 0,010 1 38,2503 20,3005
GF OPT 0,010 2 43,0723 20,2045
GF OPT 0,010 3 44,9116 22,2674
GF OPT 0,010 4 46,2428 25,172
GF OPT 0,010 6 49,1156 31,8687
GF OPT 0,001 1 38,4306 21,452
GF OPT 0,001 2 40,5867 19,8058
GF OPT 0,001 3 43,3264 20,8162
GF OPT 0,001 4 44,8305 23,0555
GF OPT 0,001 6 47,3774 28,2155
Table 4: Parameter–sweep of image guided aggregation for
the ‘Herz–Jesu’ sequence.
Agg. Cost e r
0
Level 0 Final
CB ADC 5 1 48,0009 28,2878
CB ADC 5 2 47,3767 28,2884
CB ADC 5 3 46,8367 28,5651
CB ADC 5 4 47,3276 28,7136
CB ADC 5 6 47,5468 28,5672
CB ADC 8 1 48,1184 29,9848
CB ADC 8 2 47,3707 29,2522
CB ADC 8 3 46,6911 29,4477
CB ADC 8 4 47,5492 29,4454
CB ADC 8 6 48,1225 29,5938
CB ADC 12 1 48,4898 30,3152
CB ADC 12 2 47,2583 29,5847
CB ADC 12 3 46,8833 29,7205
CB ADC 12 4 47,9632 30,0588
CB ADC 12 6 48,9818 30,7885
CB OPT 5 1 71,747 29,2853
CB OPT 5 2 66,223 29,0251
CB OPT 5 3 64,3264 29,3956
CB OPT 5 4 65,0884 29,6815
CB OPT 5 6 60,622 29,4952
CB OPT 8 1 73,0595 35,323
CB OPT 8 2 64,381 34,3963
CB OPT 8 3 62,5112 34,4801
CB OPT 8 4 62,9131 34,3226
CB OPT 8 6 58,353 29,7987
CB OPT 12 1 74,7221 35,5511
CB OPT 12 2 62,9915 34,6381
CB OPT 12 3 59,9426 34,7855
CB OPT 12 4 61,5115 34,746
CB OPT 12 6 57,2033 30,474
GF ADC 0,100 1 48,0823 31,6208
GF ADC 0,100 2 51,1138 33,5118
GF ADC 0,100 3 54,2877 36,0289
GF ADC 0,100 4 57,3762 38,4606
GF ADC 0,100 6 62,8878 40,9152
GF ADC 0,010 1 48,2435 32,5278
GF ADC 0,010 2 50,6403 33,9099
GF ADC 0,010 3 53,485 36,1495
GF ADC 0,010 4 56,2268 38,1879
GF ADC 0,010 6 61,3152 40,5947
GF ADC 0,001 1 48,3742 33,0063
GF ADC 0,001 2 49,9871 33,9849
GF ADC 0,001 3 52,6447 36,0113
GF ADC 0,001 4 55,4582 37,9339
GF ADC 0,001 6 60,3802 40,1883
GF OPT 0,100 1 55,7852 32,8818
GF OPT 0,100 2 53,0231 34,265
GF OPT 0,100 3 55,9169 36,6067
GF OPT 0,100 4 59,4258 38,9416
GF OPT 0,100 6 64,8294 41,5739
GF OPT 0,010 1 58,5235 33,8893
GF OPT 0,010 2 53,3666 34,6742
GF OPT 0,010 3 55,0431 36,8447
GF OPT 0,010 4 58,0632 38,7642
GF OPT 0,010 6 63,1551 40,9723
GF OPT 0,001 1 64,0341 34,0826
GF OPT 0,001 2 53,9388 34,7354
GF OPT 0,001 3 54,3004 36,3368
GF OPT 0,001 4 56,6877 38,252
GF OPT 0,001 6 61,6086 40,4988
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
206
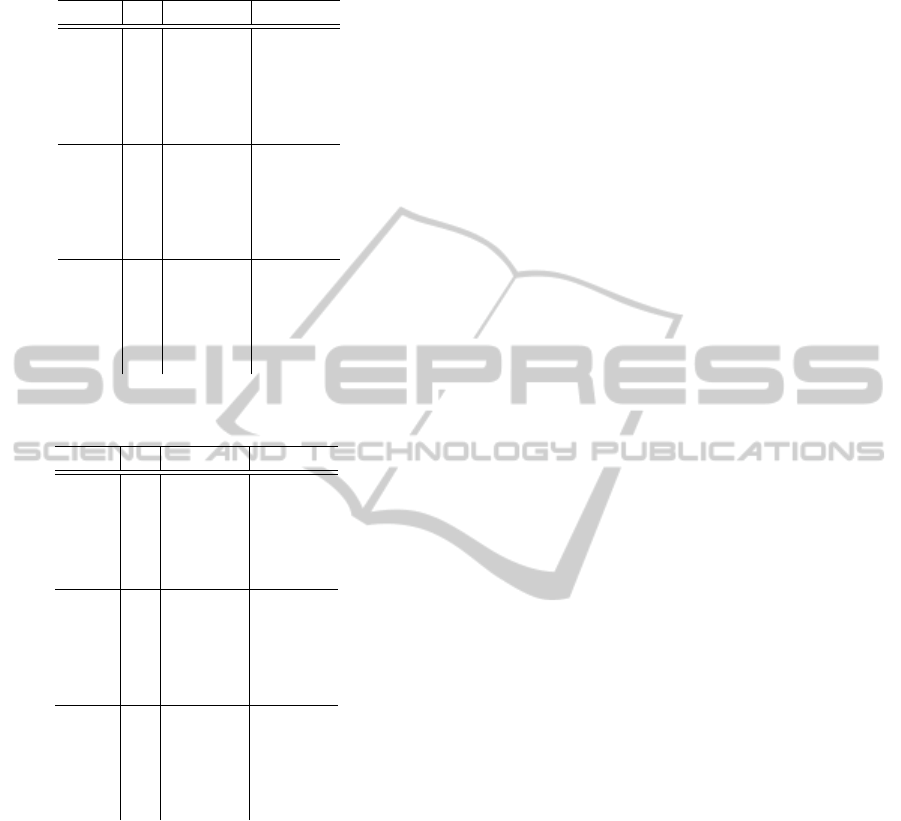
Table 5: Parameter–sweep of fixed–window aggregation for
the ‘Fountain’ sequence.
Cost r
0
Level 0 Final
SAD 1 39,3672 33,6869
SAD 2 44,57 33,7516
SAD 3 48,4126 35,219
SAD 4 51,3834 36,9954
SAD 6 57,1401 42,3865
SSD 1 39,407 31,9276
SSD 2 44,3056 28,6606
SSD 3 47,9115 31,4935
SSD 4 51,4584 36,0764
SSD 6 57,7117 43,349
NCC 1 37,5055 23,2568
NCC 2 40,3505 21,0151
NCC 3 43,9219 26,8657
NCC 4 47,4144 32,4665
NCC 6 55,3231 41,7527
Table 6: Parameter–sweep of fixed–window aggregation for
the ‘Herz–Jesu’ sequence.
Cost r
0
Level 0 Final
SAD 1 64,7667 55,4109
SAD 2 62,3676 57,3074
SAD 3 64,4764 58,7674
SAD 4 67,3589 60,8153
SAD 6 73,2592 63,8015
SSD 1 62,4588 55,9535
SSD
2 60,1193 54,717
SSD 3 63,1757 56,7857
SSD 4 67,0811 59,2385
SSD 6 73,7221 63,2108
NCC 1 50,4895 37,9934
NCC 2 45,292 41,0395
NCC 3 53,5491 44,9542
NCC 4 61,095 49,067
NCC 6 70,8198 53,7205
ImageGuidedCostAggregationforHierarchicalDepthMapFusion
207
