
Real-Time Estimation of Camera Orientation
by Tracking Orthogonal Vanishing Points in Videos
Wael Elloumi, Sylvie Treuillet and Rémy Leconge
Laboratoire Prisme, Polytech’Orléans, 12 rue de Blois, 45067 Orléans cedex2, France
Keywords: Vanishing Point Tracking, Camera Orientation, Video Sequences, Manhattan World.
Abstract: In man-made urban environments, vanishing points are pertinent visual cues for navigation task. But
estimating the orientation of an embedded camera relies on the ability to find a reliable triplet of orthogonal
vanishing points in real-time. Based on previous works, we propose a pipeline to achieve an accurate
estimation of the camera orientation while preserving a short processing time. Our algorithm pipeline relies
on two contributions: a novel sampling strategy among finite and infinite vanishing points extracted with a
RANSAC-based line clustering and a tracking along a video sequence to enforce the accuracy and the
robustness by extracting the three most pertinent orthogonal directions. Experiments on real images and
video sequences show that the proposed strategy for selecting the triplet of vanishing points is pertinent as
our algorithm gives better results than the recently published RNS optimal method (Mirzaei, 2011), in
particular for the yaw angle, which is actually essential for navigation task.
1 INTRODUCTION
In the context of navigation assistance for blind
people in urban area, we address the problem of the
pose estimation of an embedded camera. In man-
made urban environments, vanishing lines or points
are pertinent visual cues to estimate the camera
orientation, as many line segments are oriented
along three orthogonal directions aligned with the
global reference frame (Coughlan, 1999); (Antone
and Teller, 2000); (Kosecka and Zhang, 2002);
(Martins et al., 2005); (Förstner, 2010); (Kalantari et
al., 2011). Under this so-called Manhattan world
assumption, this approach is an interesting
alternative to structure and motion estimation based
on features matching, a sensitive problem in
computer vision. The orientation matrix of a
calibrated camera, parameterized with three angles,
may be efficiently computed from three noise-free
orthogonal vanishing points.
Since 30 last years, the literature is broad on the
subject of vanishing points (VP) computation. The
first approaches used the Hough transform and
accumulation methods (Barnard, 1983); (Cantoni et
al., 2001); (Boulanger et al., 2006). The efficiency of
these methods highly depends on the discretization
of the accumulation space and they are not robust in
presence of outliers. Furthermore, they do not
consider the orthogonality of the resulting VP. An
exhaustive search method may take care of the
constraint of orthogonality (Rother, 2000) but it is
off-side for real-time application.
Even few authors prefer to work on the raw
pixels (Martins et al., 2005); (Denis et al., 2008),
published methods mainly work on straight lines
extracted from image. According to the
mathematical formalisation of VP, some variants
exist in the choice of the workspace: image plane
(Rother, 2000); (Cantoni et al., 2001), projective
(Pflugfelder and Bischof, 2005); (Förstner, 2010);
(Nieto and Salgado, 2011) or Gaussian sphere
(Barnard, 1983); (Collins and Weiss, 1990);
(Kosecka and Zhang, 2002). Using Gaussian unit
sphere or projective plane allow to treat equally
finite and infinite VP, unlike image plane. This is
well suited representation for simultaneously
clustering lines that converge at multiple vanishing
points by using a probabilistic Expectation-
Maximisation (EM) joint optimization approach
(Coughlan and Yuille, 1999); (Antone and Teller,
2000); (Kosecka and Zhang, 2002) (Nieto and
Salgado, 2011). These approaches adress the mis-
classification and optimality issues but the
initialization and grouping are the determining
factors of their efficiency.
215
Elloumi W., Treuillet S. and Leconge R..
Real-Time Estimation of Camera Orientation by Tracking Orthogonal Vanishing Points in Videos .
DOI: 10.5220/0004214102150222
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 215-222
ISBN: 978-989-8565-48-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Recently, many authors adopt robust estimation
based on RANSAC, as the code is fast, easy to
implement, and requires no initialization. These
approaches consider intersection of line segments as
VP hypotheses and then iteratively clustering the
parallel lines consistent with this hypothesis
(Förstner, 2010); (Mirzaei and Roumeliotis, 2011).
A variant by J-Linkage algorithm has been used by
(Tardif, 2009). By dismissing the outliers, the
RANSAC-based classifiers are much more robust
than accumulative methods, and give a more precise
position of the VP, limited by the size of the
accumulator cell. They have been used to initialize
EM estimators to converge to the correct VP. Other
optimal solutions rely on analytical approach often
based on time-consuming algorithms (Kalantari et
al., 2011); (Mirzaei and
Roumeliotis, 2011); (Bazin et
al., 2012). In this last paper, it is interesting to note
that, even if they are non deterministic, the
RANSAC-based approaches hold comparable results
against exhaustive search for the number of
clustered lines. So, it remains a very good approach
for extracting the VP candidates, in addition with a
judicious strategy for selecting a triplet consistent
with the orthogonality constraint.
Indeed, the estimation of camera orientation
relies on the ability to find a robust orthogonal triplet
of vanishing points in a real image. Despite
numerous papers dedicated to the straight line
clustering to compute adequate vanishing points, this
problem remains an open issue for real time
application in video sequences. The estimation of
the camera orientation is generally computed in a
single image. Few works address the tracking along
a video sequence (Martins et al., 2005).
Based on previous works, we propose a
pragmatic solution to achieve an accurate estimation
of the camera orientation while preserving a short
processing time. Our algorithm pipeline relies on
two contributions: a novel sampling strategy among
finite and infinite vanishing points extracted with a
RANSAC-based line clustering, and a tracking along
a video sequence.
The paper is organized as follows. An overview
of the method is proposed in Section 2. The Section
3 presents experimental results and the Section 4
concludes the paper.
2 PROPOSED PIPELINE
The proposed pipeline is given in figure 1.
To achieve an accurate estimation of the camera
orientation based on three reliable orthogonal
vanishing points (VP), the pipeline is composed of
four steps. The first one consists on dominant line
extraction from the detected image edges. The
second one consists on selecting a triplet of
vanishing points by dominant line clustering with
RANSAC. At this step, we introduce a clever
strategy to select only three reliable orthogonal VP
that represent the orientation of the camera relative
to 3D world reference frame. Another contribution is
the vanishing point tracker performed along the
video sequences (step 3) to enforce the robustness of
the camera orientation computation (step 4). The
next sections give some details and justifications
about each bloc.
Figure 1: Overview of the proposed algorithm.
2.1 Dominant Line Detection
Some pre-processing are introduced to improve the
quality and the robustness of the detected edges in
case of embedded camera: first, an histogram
equalization harmonizes the distribution of
brightness levels in the image, secondly a geometric
correction of lenses distortion is done assuming that
the camera calibration matrix is known. To find the
dominant lines, we detect edges by using a Canny’s
detector. Then, edge points are projected into
sinusoidal curves in polar accumulation space by
applying a Hough Transform (HT), where peaks
correspond to the dominant clusters of line
segments. We use the probabilistic version of HT as
it is faster than the classic one. Only 10% or 20% of
the edges are randomly selected to obtain
statistically good results. Only the straight lines that
are long enough are selected as input to estimate
multiple VP in an image.
2.2 Vanishing Points Candidates
To provide three VP, each of them aligned with the
three main orthogonal directions of the Manhattan
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
216

world, the most intuitive method is to detect the
intersection of dominant lines in images. By
perspective projection, the parallel lines in 3D scene
intersect in the image plane in a so-called vanishing
points. If the image plane is parallel to one axis of
the 3D world, vanishing lines intersect very far from
the image center, that is called infinite vanishing
point, unlike the finite ones whose coordinates may
be determined in the image plan. Working directly in
the image plan is fast because it does not require a
projection in other bounded space like Gaussian
sphere. On the other hand, infinite VP need to be
detected separately from the finite ones, but we will
see that we can take advantage of this differentiation
in the good choice of orthogonal VP, with a fast and
robust sampling strategy.
Recently, numerous authors adopt RANSAC as a
simple and powerful method to provide a partition of
parallel straight lines into clusters by pruning
outliers. The process starts by randomly selecting
two lines to generate a VP hypothesis, then, all lines
consistent with this hypothesis are grouped together
to optimize the VP estimate. Once a dominant VP is
detected, all the associated lines are removed, and
the process is repeated to detect the next dominant
VP. The principal drawback of this sequential search
is that no orthogonality constraint is imposed for
selecting a reliable set of three VP to compute the
camera orientation. Very recent works propose
optimal estimates of three orthogonal VP by an
analytical approach based on a multivariate
polynomial system solver (Mirzaei and
Roumeliotis,
2011) or by optimization approach based on interval
analysis theory (Bazin et al., 2012), but at the
expenses of complex time-consuming algorithms.
In this work, we introduce a clever strategy to
extract a limited number of reliable VP while
enforcing the orthogonality constraint, in
conjunction with RANSAC.
2.3 VP Sampling Strategy
In the context of pedestrian navigation, the main
orthogonal directions in Manhattan world consist
generally in a vertical one (often associated with an
infinite VP) and two horizontal ones (associated
with finite or infinite VP). So we consider three
different possible configurations depending on the
alignment of the image plane with the 3D urban
scene: i) one finite and two infinite VP, ii) two finite
and one infinite VP, iii) three finite VP. The two
first configurations are common unlike the third.
More details about the computation of the camera
orientation depending on these three configurations
will be given in section 3.2.
For a robust selection of VP, we detect the three
finite candidates and two infinite ones that maximize
the consensus set. The criteria used in the consensus
score (1) for clustering lines by RANSAC are
different depending on each category. Unlike the
finite VP whose coordinates may be determined in
the image plan, the infinite VP are generally
represented as a direction. For finite VP, the
consensus score is based on a distance between the
candidate straight line and the intersecting point (2).
For infinite VP, it uses an angular distance between
the direction of the candidate straight line and the
direction representing the infinite VP (3).
,
(1)
,
1,
,
0,
(2)
where is the number of dominant lines and
,
is the Euclidian distance from the finite VP
candidate to the line
. All lines whose distance is
below a fixed threshold are considered as
participants (the threshold is equal to 4 pixels in
our experiments).
,
1, Min
,
,
,
0,
(3)
where ,
is the angle between the infinite VP
direction from the image center and the line
to test
in image space (the threshold is equal to 4° in our
experiments).
To avoid redundant VP candidates, we introduce
the supplementary constraint to be far enough from
each other: we impose on VP to have a minimum
angular distance between their directions from the
image center (threshold is set to 30° for finite VP
and 60° for infinite ones).
By separating finite from infinite VP, the
sampling strategy provides the most significant of
them without giving more importance to one or
other category (we enforce to have at least one
candidate finite). Furthermore, this clever strategy is
faster as we detect only five reliable VP candidates
against generally much more for the previous
published methods.
Among the five candidates selected before, only
three VP whose directions from the optical center
are orthogonal have to be accepted, included at least
one finite VP. We adopt the following heuristic: i)
choose the finite VP with the highest consensus
Real-TimeEstimationofCameraOrientationbyTrackingOrthogonalVanishingPointsinVideos
217

score, ii) select two other VP (finite or infinite)
based on their orthogonality to the first one, and
considering their consensus score as a second
criterion. Finally, we identify the vertical VP and the
two horizontal ones. In our application, we assume
that the camera is kept upright: we identify the
vertical VP as which presents the closest direction
with the vertical direction from the image center.
The two remaining VP are thus horizontal.
2.4 Vanishing Point Tracker
Once the whole described algorithm is processed for
the first frame of the video sequence 1, the
VP positions can be tracked from one frame to
another. Indeed, VP positions or directions are
slightly modified in video-sequences or even in a list
of successive frames. So we introduce a tracker to
check consistency between the positions of the
estimated VP in the frame and those estimated in
frame 1 . For this we use the distance between the
positions of the VP for the finite ones
,
,
and the angle between the VP directions for the
infinite ones
,
. When a VP is not coherent
with its previous position or direction, it is re-
estimated taking into account its previous position or
direction and using the remains of unclassified lines.
Hence, aberrant VP are discarded and replaced by
new VP that are, at the same time, consistent with
the previous ones and satisfy the orthogonality
constraint. This tracker is efficient since it makes our
algorithm much more stable and robust as will be
shown in the Experiments section. Once the three
most reliable VP are extracted in the image, the
camera orientation is computed frame-by-frame as
described in the next section.
2.5 Computation of the Camera
Orientation
This part is directly inspired from (Boulanger et al.,
2006) to compute the camera orientation from the
three VP supposed to be orthogonal.
We use the directions of the detected VP which
correspond to the camera orientation to compute the
rotation matrix
,,
. The vectors
,and
to
be found represent three orthogonal directions of the
scene, respectively the first horizontal direction, the
vertical direction and the second horizontal
direction. They need to satisfy the following
orthonormal relations:
.
.
.
0
‖
‖
‖
‖
‖
‖
1
(4)
The estimation of these vectors depends on the
VP configurations.
2.5.1 One Finite and Two Infinite VP
This situation is the most frequent one. It occurs
when the image plane is aligned with two axis of the
world coordinate frame. Let be the finite VP and
the focal length. The direction of can be expressed
as
,
,
whereas the directions of
the infinite VP, in image space, are
,
,0
and
,
,0
. The vectors of
the rotation matrix are given by the following
system of equations:
,
,
,
,
,
,
(5)
2.5.2 Two Finite and One Infinite VP
This situation happens when the image plane is
aligned with only one of the three axis of the world
coordinate frame. Let
and
be the two finite VP
of directions
,
,
and
,
,
. Since there are two finite horizontal
VP, we set
to the closest VP to the image center.
The vector is obtained by cross product as shown
in the system of equations below.
,
,
,
,
(6)
2.5.3 Three Finite VP
This last configuration is the least frequent one. It
occurs when there is no alignment between the
image plane and the world coordinate frame. Let
,
and
be the three finite VP of directions
,
,
,
,
,
and
,
,
. We start by setting to the
VP whose direction is closest to the vertical
direction. We then set
to the closest VP to the
image center. In the system of equations (7), we
assume that
is the vertical VP and
is closest to
the image center.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
218

,
,
,
,
,
,
(7)
3 EXPERIMENTAL RESULTS
This section presents the performance evaluation of
the proposed method.
3.1 Accuracy Study
For comparison purpose, we have tested our
algorithm facing the ground truth provided with the
public York Urban Database (YUD). This database
provides the original images, camera calibration
parameters, ground truth line segments, and the three
Euler angles relating to the camera orientation for
each image (Denis et al., 2008). Figure 2 illustrates
some orthogonal vanishing points and their
associated parallel lines extracted by our algorithm
on some images pulled out the YUD.
The Table 1 presents the angular distance from
Ground Truth (GT) of the camera orientation
computed with our method. The average and
standard deviation of the angular distance are
performed on a set of fifty images for the three
angles. The three last rows of the Table 1 give the
number of times the distance exceeds a fixed value
of 2, 5 and 10 degrees respectively. Our method
performs accurate estimates of the camera
orientation since the angular distance remains
inferior to 2 degrees for the most images. For
comparison purpose, the analytical method RNS
recently published by (Mirzaei and Roumeliotis,
2011), that provides optimal least-squares estimates
of three orthogonal vanishing points, performs an
average angular distance of 0.74 degree, 1.70 and
1.81 degrees for pitch, yaw, roll angles respectively.
The full results of the RNS method are available in a
technical report provided online by the authors
(http://umn.edu/~faraz/vp).
The RNS method gives the best result for the
pitch angle but it is interesting to note that our
method is significantly better for the yaw and roll
angles. The yaw is actually essential for a pedestrian
navigation task since it gives the camera viewing
direction. This may be explains by our clever
strategy for selecting orthogonal vanishing points
that are distant enough from each other without
confusion between finite and infinite points.
Table 1: Average and standard deviation of the angular
distance from the GT (in degrees).
Angular distance from GT
pitch yaw roll
Average
1,38 0,75 0,69
Standard deviation
1,57 0,60 0,65
> 2°
8 3 1
> 5°
2 0 0
> 10°
0 0 0
3.2 Tracking the Camera Orientation
To show the efficiency of our algorithm for tracking
the camera orientation, we acquire real video
sequences, with an embedded camera. Our
experimental prototype is composed of a camera
AVT GUPPY F-033C equipped with a 3.5mm lens
and a laptop. As we use a lens with a short focal
length, it is recommended to apply a geometric
distortion correction before extracting line segments.
The camera has been first calibrated using the tool:
http://www.vision.caltech.edu/bouguetj/calib_doc/, a
software proposed by Bouguet.
Figure 3 depicts some typical results of
vanishing point extraction for a video sequence. It is
composed of 350 frames (320x240 pixels) acquired
at 25 frames per second in the hallways of our
laboratory. Figure 4 compares the evolution of the
roll, pitch and yaw angles of the camera orientation
along the video sequence by applying our method
with and without the vanishing point tracker (VPT).
The VPT produces a smooth running and a more
reliable estimation for camera orientation along the
video sequence.
Since the VPT removes some
aberrant vanishing points, keeping only the points
that are consistent, we then obtain a more accurate
camera orientation.
Figure 2: Examples of some triplets of orthogonal vanishing points detected by our algorithm on images from the YUD.
Real-TimeEstimationofCameraOrientationbyTrackingOrthogonalVanishingPointsinVideos
219
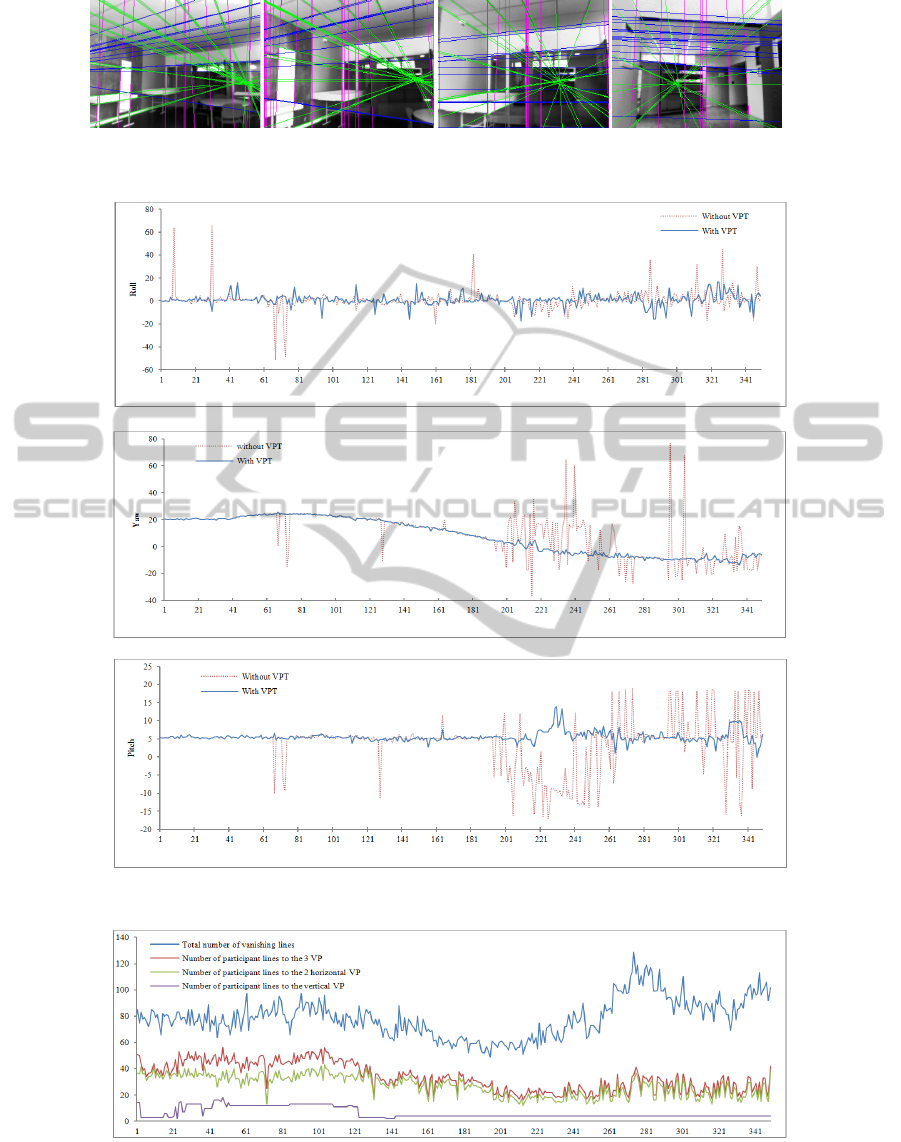
Figure 3: Examples of detection and tracking of triplets of orthogonal vanishing points and their associated lines.
Figure 4: Smoothing effect of the VPT on the estimation of the camera’s orientation (pitch, yaw and roll angles).
Figure 5: Evolution of the total number of lines extracted in images and the numbers of lines respectively associated to
horizontal and vertical VP along the video sequence.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
220

To illustrate the efficiency of the proposed
sampling strategy of vanishing points based on line
clustering with RANSAC, figures 5 shows the
evolution of the number of vanishing lines extracted
along the video sequence. The figure represents the
total number of vanishing lines together with the
number of participant lines to the 3 VP (inliers),
shared into the subset of lines associated to the 2
horizontal VP and the subset the lines associated to
the vertical VP. It is clear that by using RANSAC-
based classification of lines, the method removes the
outliers.
Our method has been implemented by using
visual c++ and opencv library. The full processing
time for estimating the camera orientation takes 16
milliseconds per image of size 320x240 pixels with
non-optimized code on a laptop (intel core 2 duo
2.66ghz/4096mb). Therefore, our algorithm is
suitable for real time applications, such as
navigation assistance for blind pedestrian.
4 CONCLUSIONS
We take advantage of three reliable orthogonal
vanishing points corresponding to the Manhattan
direction to achieve accurate estimation of the
camera orientation. Our algorithm relies on a novel
sampling strategy among finite and infinite
vanishing points and a tracking along a video
sequence. The performance of our algorithm is
validated using real static images and video
sequences. Experimental results on real images,
show that, even simple, the adopted strategy for
selecting three reliable distant and orthogonal
vanishing points in conjunction with RANSA
performs well in practice since the estimation of the
camera orientation is better than those obtained with
a state-of-art analytical method. Furthermore, the
tracker proved to be relevant to dismiss aberrant
vanishing points along the sequence, making
outmoded refinement or optimization later step and
preserving a short processing time for real-time
application. This algorithm is devoted to be a part of
a localization system that should provides navigation
assistance for blind people in urban area.
ACKNOWLEDGEMENTS
This study is supported by HERON Technologies
SAS and the Conseil Général du LOIRET.
REFERENCES
M. Antone and S. Teller, 2000. Automatic recovery of
relative camera rotations for urban scene. In: Proc. of
IEEE Conf. Computer Vision and Pattern recognition
(CVPR) 282-289.
S. T. Barnard, 1983. Interpreting perspective images.
Artificial Intelligence, 21(4), 435-462, Elsevier
Science B.V.
J. C. Bazin, Y. Seo, C. Demonceaux, P. Vasseur, K.
Ikeuchi, I. Kweon and M. Pollefeys, 2012. Globally
optimal line clustering and vanishing points estimation
in a Manhattan world. In: the IEEE Int. Conf. on
Computer Vision and Pattern Recognition (CVPR).
K. Boulanger, K. Bouatouch, and S. Pattanaik, 2006.
ATIP : A tool for 3D navigation inside a single image
with automatic camera calibration. In: EG UK Conf on
Theory and Practice of Computer Graphics.
V. Cantoni, L. Lombardi, M. Porta and N. Sicard, 2001.
Vanishing Point Detection: Representation Analysis
and New Approaches. In : Proc. of Int. Conf. on Image
Analysis and Processing (ICIAP), 90-94.
R. T Collins and R. S Weiss, 1990. Vanishing point
calculation as statistical inference on the unit sphere.
In: Proceedings of the 3rd Int. Conference on
Computer Vision (ICCV), 400-403.
J. M. Coughlan and A. L. Yuille, 1999. Manhattan World:
Compass direction from a single image by Bayesian
inference. In: Int. Conference on Computer Vision
(ICCV).
P. Denis, J. H. Elder and F. Estrada, 2008. Efficient Edge-
Based Methods for Estimating Manhattan Frames in
Urban Imagery. In: European Conference on
Computer Vision (ECCV), 197-210.
W. Förstner, 2010. Optimal vanishing point detection and
rotation estimation of single images from a legoland
scene. In: Proceedings of the ISPRS Symposium
Commision III PCV. S. 157-163, Part A, Paris.
M. Kalantari, A. Hashemi, F. Jung and J.P. Guédon, 2011.
A New Solution to the Relative Orientation Problem
Using Only 3 Points and the Vertical Direction.
Journal of Mathematical Imaging and Vision archive
Volume 39(3).
J. Kosecka and W. Zhang, 2002, Video Compass, In Proc.
of the 7th European Conf. on Computer Vision
(ECCV).
A. Martins, P. Aguiar and M. Figueiredo, 2005.
Orientation in Manhattan world: Equiprojective
classes and sequential estimation. In: the IEEE Trans.
on Pattern Analysis and Machine Intelligence, Vol. 27,
822-826.
F. M. Mirzaei and S. I. Roumeliotis, 2011. Optimal
estimation of vanishing points in a Manhattan world.
In: the Proc. of IEEE Int. Conf. on Computer Vision
(ICCV).
M. Nieto and L. Salgado, 2011. Simultaneous estimation
of vanishing points and their converging lines using
the EM algorithm. Pattern Recognition Letters, vol.
32(14), 1691-1700.
Real-TimeEstimationofCameraOrientationbyTrackingOrthogonalVanishingPointsinVideos
221

R. Pflugfelder and Bischof, 2005. Online auto-calibration
in man-made world. In: Proc. Digital Image
Computing : Techniques and Applications, 519-526.
C. Rother, 2000. A new approach for vanishing point
detection in architectural environments. In: Proc. of
the 11th British Machine Vision Conference (BMVC),
382-391.
J.-P. Tardif, 2009. Non-iterative approach for fast and
accurate vanishing point detection. In: Proc. Int.
Conference on Computer Vision (ICCV), 1250-1257.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
222
