
Identification of Pronation-supination Patterns on Runners
An Aplication of Functional Principal Component Analysis
E. Medina
1
, H. De Rosario
1
, J. Olaso
1
, A. Ballester
1
, J. Navarro
1
and A. Page
2,3
1
Instituto de Biomecánica de Valencia, Valencia, Spain
2
Departmento de física Aplicada,Universidad de Politécnica Valencia, Valencia, Spain
3
Grupo de Tecnología Sanitaria del IBV
CIBER de Bioingeniería, Biomateriales y Nanomedicina (CIBER-BBN), Zaragoza, Spain
Keywords: Running, Pronator, Functional Data Analysis, Functional Principal Component Analysis.
Abstract: The correct classification of runners according to their gait patterns is a relevant issue for the design of
sports footwear. Specifically, the classification of runners as neutral, pronators, and supinators is a problem
that is not yet fully solved, and requires expert observation, since current models based on the automatic
processing of kinematic measures are very limited. This work proposes a method based on Functional Data
Analysis (FDA) for automatically describing the morphology of the curves that represent ankle movement
patterns. By Functional Analysis of Principal Components, the information contained in each data stream is
reduced to a small set of variables, that allows an efficient classification of subjects.
1 INTRODUCTION
In recent years, there has been an increment in the
practice of running. In spite of the evident
advantages of sports practice, running has some
health risks, as any other physical activity. One of
the risk factors is the inadequacy of footwear to the
runner’s characteristics. Specifically, the excess of
pronation or supination has been described as one of
the most frequent causes of injury in urban races
(Hintermann and Nigg, 1998; Nester et al, 2003;
Branthwaite et al., 2004).
Classifying a runner as normal, pronator, or
supinator , currently requires the expert judgment of
a professional, and it is not easy to do automatically.
Most specialists use qualitative methods based on
observing the orientation of body parts during the
support stance (Kapandji, 1987; Stell and Buckley,
1998). Many research studies use video-
photogrammetry in order to measure pronation and
supination as the maximal inversion-eversion angle
during the support phase (Perry and Lafortune,
1995; McClay, 1998).
However, the attempts to develop automatic
systems for such a classification have not led to
good results. First, inversion-eversion measures
show a relevant dispersion, and it is difficult to
establish clear limits (Stacoff et al., 2000). Besides,
multivariate classification requires using many
variables, and such systems usually have robustness
issues (Stefanyshyn et al., 2003). Moreover,
defining the variables that characterize the gesture is
not a trivial task, since it is highly dependent on the
shape of the motion curves, which do not always
show easily identifiable patterns. Finally, the
parameterization of the curves implies a loss of
information, since any limited set of parameters
cannot convey the whole continuous information of
a function recorded over time.
One possibility to overcome those limitations is
Functional Data Analysis (FDA). Instead of
extracting scalar parameters from a curve (such as
maxima, minima, phase durations, etc.), this
statistical technique works with time functions that
consider each curve as a single datum (Ramsay and
Silverman, 2005). FDA has been used to generalize
many classic statistical techniques, such as principal
component analysis (FPCA) (Ramsay and Dalzell,
1991). FPCA allows describing the variability
associated to a set of curves, in order to reduce
continuous information into a small set of
independent variables, while maintaining all the
information of original curves (Epifanio et al.,
2008).
The goal of this study was to define a procedure
for classifying runners in three groups: neutral,
294
Medina E., de Rosario H., Olaso J., Ballester A., Navarro J. and Page A..
Identification of Pronation-supination Patterns on Runners - An Aplication of Functional Principal Component Analysis.
DOI: 10.5220/0004215102940297
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 294-297
ISBN: 978-989-8565-36-5
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
pronators and supinators by using video-
photogrammetry three-dimensional records of
continuous motion. The method uses Functional
Principal Component Analysis (FPCA) to obtain a
reduced set of principal factors as data, which are
used for characterizing the subject groups and for
defining a classification model of individuals.
2 METHODS
2.1 Sample of Study
The study sample consisted on 14 assiduous male
runners aged from 21 to 50. The runners were
selected from the competitors of the 32nd Valencia
marathon, and a Sports Society in Valencia called
‘Correcaminos’ (Road Runner), specialized in
athletics and trekking. These were all heel strikers,
and did not suffer any current injury.
2.2 Clinical Assessment
A footcare specialist performed a clinical evaluation
of the users’ lower limb, carrying out an anamnesis,
as well as a static assessment of the characteristics
and morphology of their legs, including ankles and
feet, using exploration techniques and a podoscope
for recording the shape of the foot’s plant. This
information was used to classify the runners into
three groups: normal, pronator and supinator
runners.
2.3 Biomechanical Analysis
Each runner performed four trials with two footwear
models, so that there were 112 observations in total.
During the study, subjects were asked to run at a
fixed and controlled speed of 5 minutes/km, that is,
12 km/h. In addition, the testing order of the
footwear models was randomized, so learning
effects were eliminated.
Motion of lower limb and footwear were
recorded by using videophotogrammetry
(Kinescan/IBV, Page et al 2009). A set of reflective
markers were placed at anatomical places according
to the protocol described in (Wu et al., 2002). The
gestures were recorded at 250 fps. The movement of
markers was analyzed to measure flexion-extension,
axial rotation, and inversion-eversion angles, using
the algorithm of kinematical analysis described in
Page et al. (2009). Three curves were taken for each
record, corresponding to the time functions of those
angles.
2.4 Data Processing and Statistical
Analysis
The support phase of each record was extracted by
trimming the original signal. The data streams were
smoothed by a base of B-splines, as described in
Ramsay et al. (2005), and time scales were linearly
adjusted in order to express the evolution of the
movement as a percentage of the support time.
FPCA was applied separately to the three angles
(flexion, rotation and inversion-eversion) using the
whole set of 112 observations for each angle. This
technique defines a base of independent functions
that can be combined some way to explain all the
observed variability. Thus, for the observed i-th
function f
i
(t),
f
i
(t) = F(t) + a
i1
PC
1
(t) + a
i2
PC
2
(t) +...
...a
i
m
PC
m
(t)
(1)
where F(t) is the functional average of f
i
(t) for all
observations, PC
j
(t) are the functional principal
components, and a
ij
are the scores of the i-th
observation for component PC
j
(t). The full
calculation procedure is described by Epifanio et al,
(2008).
These data were used to define a classification
model by linear discriminant analysis. The
independent variables were the a
ij
scores, whereas
the model was trained by the classification in three
levels (neutral, pronator, or supinator) of the
participants, according to the opinion of an expert.
All calculations were performed in MATLAB.
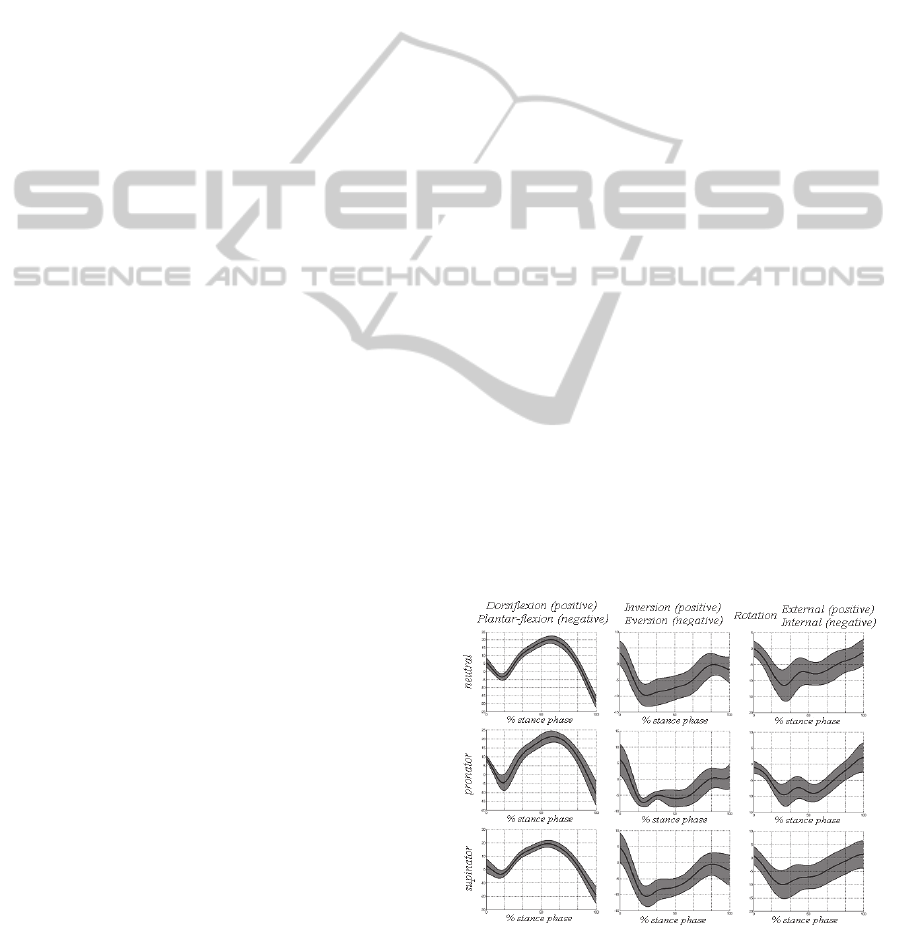
Figure 1: Movement patterns for each group.
IdentificationofPronation-supinationPatternsonRunners-AnAplicationofFunctionalPrincipalComponentAnalysis
295

Figure 2: Results of FPCA for the eversion angle. Each graphics represents the functional mean (solid black line) and the
mean plus or minus the sd(a
ij
) PC
j
(t).
3 RESULTS AND DISCUSSION
Figure 1 show the averages and standard deviations
of the three angles measured for each group. As can
be seen in the graphs, there are qualitative
differences between groups, although it is not easy
to quantify them, since each group has a different
number of local maxima and minima.
Figure 2 shows the results of the FPCA for the
eversion angle (EVE). This analysis was also
applied to the other angles, rotation (ROT) and
flexion (FE) but only the case of eversion is shown
because it is the most relevant one for the attempted
classification. Each plot represents the functional
mean (solid black line) and the mean plus or minus
the sd(a
ij
) PC
j
(t). This representation allows
assigning an intuitive meaning to each component.
Thus, PC1-EVE is an “offset” factor, related to
the general position of the whole curve in the Y-
axis. PC2-EVE is related to the range of the first
support phase, and the moment where maximal
eversion is seen. PC3-EVE indicates the differences
in the signal shape, so that high scores are associated
to lower ranges and two local minima, whereas
negative scores are related to broader ranges and just
one minimum. Finally, PC4-EVE is mainly related
to the final value of eversion before taking off.
The first four principal components explained
97.3% of the observed variance. Likewise, 4 factors
explained 97.5% of variance in flexion-extension
angles, and further 4 factors explained 96.2% of
axial rotation variance. Thus, FPCA allows
representing the whole information contained in the
curves with just 4 variables. This is an important
improvement with respect to classical methods,
which require identifying specific landmarks and use
many variables (Stacoff et al, 2000; Cheung and Ng,
2007)
Table 1 shows the coefficients of the two
discriminant functions (LD1, LD2) that were
obtained in the discriminant analysis, using PCj. as
independent variables. Figure 3 shows a scatter plot
of these functions for the observed values.
Table 1: Classification results.
PC
1FE
PC
3EVE
PC
2ROT
PC
2FE
PC
1EVE
PC
3FE
PC
4ROT
LD1 0.61 0.60 -0.37 -0.41 0.24 0.10 -0.12
LD2 -0.13 0.013 -0.48 0.09 0.07 -0.53 0.61
As can be seen in Figure 3, LD1 clearly separates
between pronators (high values) from the rest of
subjects; and this function specially depends on the
first and third components of eversion, (PC1-EVE,
PC3-EVE) the first component of flexion-extension
(PC1-FE), and the second component of axial
rotation (
PC2-ROT) (see Table 1).
The distinction between supinators and neutrals
is less clear, and it depends on a combination of LD1
and LD2. This function is associated to the fourth
and second component of axial rotation angle, and to
the third component of flexion-extension.
Figure 3: Scatterplot of observations for discriminant
function coefficients.
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
296

Finally, Table 2 shows the results of the
classification obtained by a “leave-one-out” cross-
validation. The classification is fairly good for
pronators, who are clearly discriminated from the
rest, but not that good for the supinators.
These results show that it is possible to classify
runners from kinematical variables by means of
FDA, in contrast with the lack of correspondence
between clinical and biomechanical criteria that has
been reported in previous works (Stefanyshyn,
2003).
Table 2: Classification results.
Prediction
Group P N S Success
P (24) 21 2 1 88%
N (64) 1 57 6 89%
S (24) 0 9 15 63%
4 CONCLUSIONS
Using functional data is advantageous for the
statistical treatment of time functions. FPCA in
particular allows reducing the information of a
family of curves to a small set of scalar variables,
automatically and without loss of the original
information that is contained in the raw signals.
This technique has been applied to the
classification of runners as neutral, pronators, or
supinators. The scores of the principal components
allowed to distinguish clearly between pronators and
the result of population, whereas the separation
between neutrals and supinators will require further
data processing, like analyzing the movement of the
distal part of the foot.
This technique has clear advantages for the
extraction of scalar variables form curve
characteristics: it does not require a pre-processing
of the function, and it allows using curves of
different morphologies, since that information is
already included in the principal components.
ACKNOWLEDGEMENTS
This research has been partially supported by
Seventh Framework Program of the EC (Project
Fit4U, NMP2-SE-2009-229336), and by the
Spanish Government with co-financiation of UE
FEDER funds (Grant DPI2009-138030-C02 01 and
02 and IMPIVA IMDEEA/2011/93 and
IMDEEA/2011/50).
REFERENCES
Branthwaite, H. R. Payton, C. J., Chockalingam, N.
(2004). The effect of simple insoles on three-
dimensional foot motion during normal walking.
Clinical Biomechanics, 19(9), pp 972–977.
Cheung, R. T. H, Ng, G. Y. F. (2007). Efficacy of motion
control shoes for reducing excessive rearfoot motion
in fatigued runners. Physical Therapy in Sport, 8(2),
pp 75–81.
Epifanio, I., Ávila, C., Page, A. and Atienza, C. (2008).
Analysis of multiple waveforms by means of
functional principal component analysis: normal
versus pathological patterns in sit-to-stand movement.
Medical and Biological Engineering and Computing,
46, pp 551–561.
Hintermann B., Nigg, B. M. (1998). Pronation in
Runners: Implications for Injuries . Sports Medicine,
26(3), pp. 169-176.
Kapandji, I. A. (1987). Physiology of the joints. The lower
limb. Churchill Livingstone Ed.
McClay, I., Manal, K., (1998). A comparison of three-
dimensional lower extremity kinematics during
running between excessive pronators and normals.
Clinical Biomechanics, 13(3), pp 195-203.
Nester, C. J., M. L van der Linden, M. L., P Bowker, P.
(2003). Effect of foot orthoses on the kinematics and
kinetics of normal walking gait. Gait and Posture,
17(2), pp 180–187.
Page, A., de Rosario, H., Mata, V., Atienza, C., (2009).
Experimental analysis of rigid body motion. A vector
method to determine finite and infinitesimal
displacements from point coordinates. Journal of
Mechanical Design 131, 031005 (8 pp.).
Perry,S. D., MA Lafortune, M. A. (1995). Influences of
inversion/eversion of the foot upon impactloading
during locomotion. Clinical Biomechanics, 10(5), pp
253–257.
Ramsay J, Dalzell C (1991) Some tools for functional data
analysis. J R Stat Soc Ser B Methodol 3(3):539–572.
Ramsay J. O., Silverman B. W. (2005) Functional data
analysis. Springer, New York.
Stacoff, A., Reinschmidt, C., Nigg, B. M., van den Bogert,
A.J., Lundberg, A., Denoth, J., Stüssi, E. (2000).
Effects of foot orthoses on skeletal motion during
running. Clinical Biomechanics, 15(1), pp 54–64.
Stefanyshyn DJ, Stergiou P, Nigg BM, et al. (2003). Do
pronators pronate? 6th Symposium on Footwear
Biomechanics, Queenstown, New Zealand, July 2003.
Stell, J. F., Buckley, J. G. (1998). Controlling excessive
pronation: a comparison of casted and non-casted
orthoses. The Foot, 8(4), pp. 210–214.
Wu, G. et al. (2002) ISB recommendation on definitions
of joint coordinate system of various joints for the
reporting of human joint motion. Part I ankle, hip and
spine. Journal of Biomechanics 35, pp: 543-548.
IdentificationofPronation-supinationPatternsonRunners-AnAplicationofFunctionalPrincipalComponentAnalysis
297
