
A Statistical Model for Coupled Human Shape and Motion Synthesis
Alina Kuznetsova
1
, Nikolaus F. Troje
2
and Bodo Rosenhahn
1
1
Institute for Information Processing, Leibniz University Hanover, Hannover, Germany
2
Bio Motion Lab, Queen’s University, Kingston, Canada
Keywords:
Animation, Shape and Motion Synthesis, Statistical Modeling.
Abstract:
Due to rapid development of virtual reality industry, realistic modeling and animation is becoming more and
more important. In the paper, we propose a method to synthesize both human appearance and motion given
semantic parameters, as well as to create realistic animation of still meshes and to synthesize appearance based
on a given motion. Our approach is data-driven and allows to correlate two databases containing shape and
motion data. The synthetic output of the model is evaluated quantitatively and in terms of visual plausibility.
1 INTRODUCTION
Emerging interest in 3D technologies and virtual real-
ity introduced a need for realistic computer modeling
and animation. It is a rapidly developing area and yet
there are many unresolved problems, such as fast and
realistic character creation. In this paper, we propose
a statistical model to solve the latter problem.
In general, character creation is a challenging
task. The character generation problem is addressed
either by manual editing and 3D modeling or by
data-driven approaches; a well-known example of ap-
pearance creation is the SCAPE model (Anguelov
et al., 2005). Motion simulation is usually con-
sidered as a separate topic, where three types of
methods exist: manual motion editing, physics-based
approaches and data-driven approaches. The old-
est approach is manual motion editing, such as key
frame animation. However, manual editing is not
able to provide enough level of motion detailization
and is very time-consuming, therefore data-driven ap-
proaches emerged recently, as well as physics based
and control-based methods. Unfortunately, data-
driven approaches usually produce physically incor-
rect results and the question of fitting generated mo-
tion to the concrete character (motion retargeting) is
not solved completely; physics-based approaches are
usually very computationally-intensive and complex,
do not provide enough variability and, as experiments
showed, physical fidelity of motion does not imply vi-
sual plausibility. Another way to animate a new char-
acter is to transfer motion from another character, but
when the characters have different parameters (such
as proportions, height, etc), such transfer can produce
unrealistic results (so-called retargeting problem), as
shown on the Fig 1. Here, the same shape was an-
imated using different motions, one of which comes
from a person with similar biometric parameters and
the other is the motion of the person with completely
different biometric parameters. Even from a sequence
of images it is possible to see a mismatch between the
shape and the motion.
The other disadvantage of the approaches de-
scribed above is that they are difficult to apply, when
the task is to animate many characters at once.
In this work, we propose a model for character ap-
pearance creation and animation by combining a sta-
tistical model of human motion with one for character
appearance. In this way we address the problems de-
scribed above. We are able to generate both the char-
acter’s appearance and motion simultaneously, there-
fore avoiding the retargeting problem and extensive
computations, while still producing visually plausi-
ble animations. Semantic parameters, such as weight,
height and proportions of the character, serve as a link
between shape and motion, and are integrated in our
model, allowing excellent control over the generation
process. Since our model is stochastic, it can be used
for random character generation.
Our paper is organized in the following way. In
Section 2, we give a short overview of existing meth-
ods for character generation and animation. In Sec-
tion 3, we give technical details about data collection
and processing. In Section 4 we explain the model we
use for generation. In Section 5, we provide an eval-
uation of our approach in terms of visual perception
227
Kuznetsova A., Troje N. and Rosenhahn B..
A Statistical Model for Coupled Human Shape and Motion Synthesis.
DOI: 10.5220/0004215602270236
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (GRAPP-2013), pages 227-236
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b)
Figure 1: Example of motion retargeting problem: (a) red figure unrealistically bends backwards, while green figure has
correct balance; (b) red figure has its shoulders set backwards, as is typical for slimmer person.
of generated characters and their motions, as well as
a quantitative assessment of an appearance-to-motion
fit.
2 RELATED WORKS
In this section, we revise already existing works on
motion and shape modeling. Since standard ap-
proaches to this problem separate creation of charac-
ter and creation of its motion, we first provide a short
review of methods proposed for both problems.
Motion Simulation Techniques. Many techniques
address the motion simulation problem. A purely
data-driven approach for motion simulation was in-
troduced by (Wang et al., 2008) and is based on Gaus-
sian process models for motion generation; (Li et al.,
2002) proposed to use linear dynamic systems with
distribution of the dynamic system parameters to con-
trol the generation; (Brand and Hertzmann, 2000)
used style machines to create variations in one type
of motion. Finally, (Troje, 2002) used Principal Com-
ponent Analysis (PCA) analysis to build a manifold
of cyclic motions.
Another approach to motion synthesis is in com-
bining already existing motions without usage of any
statistical models, for example, in (Sidenbladh et al.,
2002), no motion is synthesized, but the closest real
motion in the database of motions is found based on
predefined metrics.
Physics-based models of human motion, such as
proposed in (Liu et al., 2005), are used to make mo-
tion physically plausible, which is often required for
animation of interactions. More frequently, however,
different types of controllers are used to refine al-
ready generated motion, for example as proposed in
(da Silva et al., 2008; Lee et al., 2009; Popovic and
Witkin, 1999; Sok et al., 2007).
Mesh Simulation Techniques. The traditional way
of creating character appearance is manual modeling.
Recently, automated approaches were presented, such
as the SCAPE model (Anguelov et al., 2005), that is
now state-of-the-art technique. A slightly different
statistical model is presented in (Hasler et al., 2009).
Here, the use of semantic “handles” is also proposed
to achieve variability of shapes.
Our Contribution. In contrast to the above men-
tioned works, where mesh and motion are clearly sep-
arated, we propose to combine appearance creation
with motion simulation, therefore avoiding many
problems of motion retargeting. To our knowledge,
there are no previous works bringing motion simula-
tion and shape creation together. We apply the model
to generate joint realistic human shape and motion.
We also see our contribution in developing
a method to find dependencies in two separate
databases and building a model, that allows to unite
the data from both databases, using the dependencies
found.
In general, we can imagine many applications
of the model, for example, crowd simulation, au-
tomatic animation of already existing characters or
appearance-from-motion reconstruction. In mathe-
matical sense, our model is inspired by variational
models, proposed in (Cootes et al., 2001). However,
we include a random component and therefore allow
for more loose coupling of motion and shape, as well
as for variability in sampled characters.
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
228

40 50 60 70 80 90 100 110
0
10
20
(a) Weight
150 160 170 180 190
0
5
10
(b) Height
10 20 30 40 50 60
0
10
20
30
(c) Age
40 50 60 70 80 90 100 110
0
10
20
(d) Weight
150 160 170 180 190
0
5
10
(e) Height
10 20 30 40 50 60
0
10
20
30
(f) Age
Figure 2: Distribution of the semantic parameters (weight, height, age) of females in the databases. The upper row shows
parameter distribution for the shapes dataset; the lower row shows parameter distribution for the motion dataset.
3 DATA PREPARATION
3.1 Data Preprocessing
Since our model is purely data-driven, we first give
insights of data preprocessing.
To train the model we need two sources of data:
body scans to learn human appearance, or shape,
and motion data, collected during recording session.
These two databases contain shapes and motions,
recorded from the different people, although the dis-
tribution of their semantic parameters are approxi-
mately the same.
The shape database (Hasler et al., 2009) contains
body scans of 114 different subjects. Body scans were
previously registered, such that aligned meshes, con-
taining N = 1002 vertices, were produced.
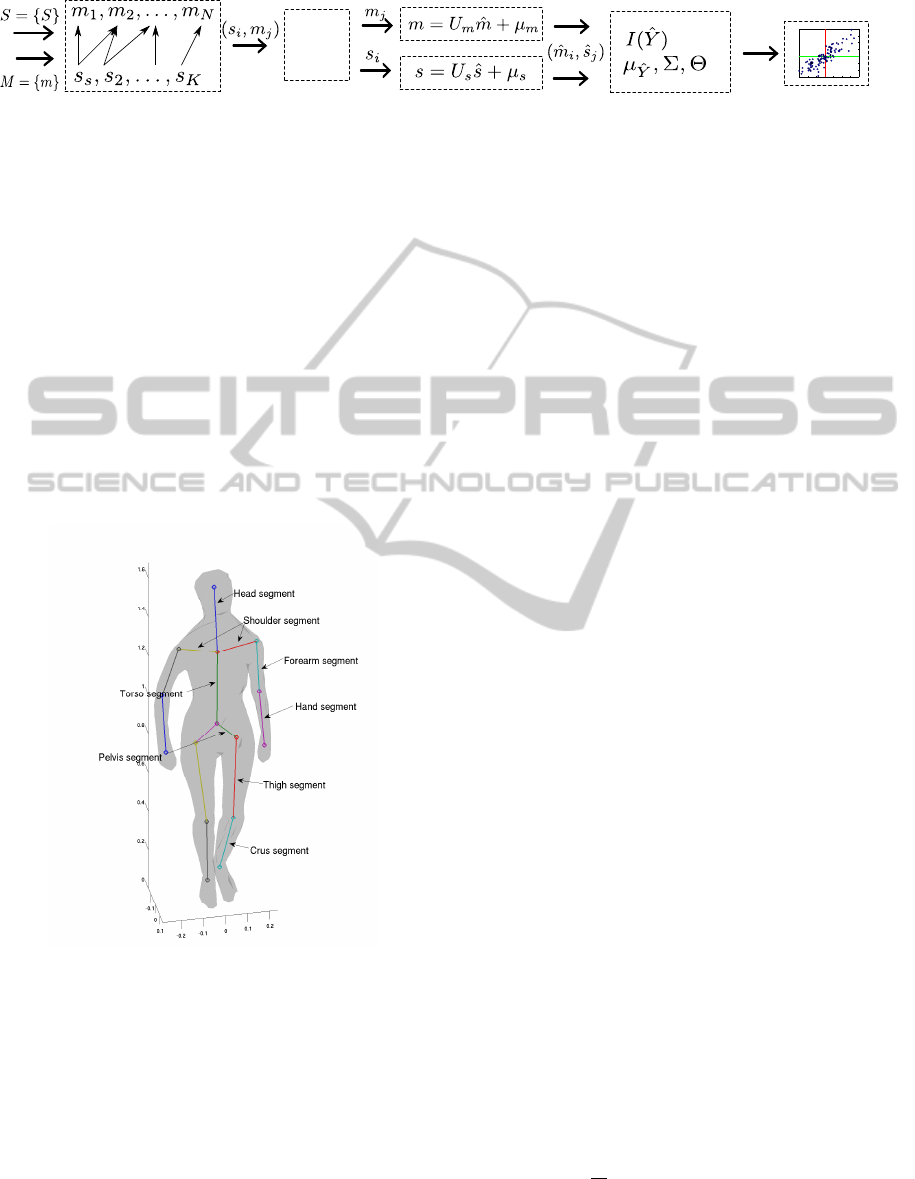
Into each mesh we embed a skeleton (see Fig. 4),
consisting of K = 15 joints, and morph meshes in such
a way, that the skeletons of these meshes are exactly
in the same pose. This is done to exclude variability in
shapes due to slight differences in pose. We compute
the skeleton’s joints’ positions as a linear combination
of nearby vertices:
s
k
=
N
∑
i=1
ω
ik
v
i
, (1)
where weighs ω
ik
were derived manually based on the
procedure, that was used to place markers on the body
during the creation of the motion database.
As a source of motion data, we used the motion
database, described in (Troje, 2002); the database
contains recordings of gait motion of 100 individu-
als. Firstly, motion was acquired using MoCap sys-
tem with 45 markers. From 45 physical markers
K = 15 virtual markers were derived; these mark-
ers correspond to the placement of skeleton joints in-
side the mesh. For each motion 4 so-called eigenpos-
tures are extracted. Each motion is then represented
as a linear combination of eigenpostures, where the
coefficients are periodical functions, that depend on
time. The walk cycle parameter is individual for
each person and therefore is stored separately. That
means, that all together each motion is represented
with K ·3 ·(4 + 1) + 1 coordinates.
Moreover, for each person semantic data, such as
gender, weight, heights, age, was stored. We denote
semantic attributes, connected to each recorded shape
s or motion m, as v(s) or v(m). Firstly, we separated
male from female subjects in both databases, since
variation between male and female meshes is much
greater then the variation within the female (or male)
part of the database itself and such separation makes
our model able to better capture variation within both
groups. Each group has the same number of mem-
bers, i.e 55 females and 59 males in the mesh database
and 50 females and 50 males in the motion database.
The distributions of the semantic parameters of fe-
males are presented in Fig. 2. For our experiments,
we took weight and height as the most varying pa-
rameters across our data sets, but in general any set
of parameters could have been taken, as long as it has
significant influence on shape appearance and on mo-
tion.
3.2 Binding a Skeleton to a Mesh
Since the motion data we obtained is represented us-
ing positions of joints depending on time, we chose to
use a skeleton-based approach to animate the model.
Several methods are proposed to solve the problem of
skeleton-based character animation. As mentioned in
the previous subsection, we embedded a skeleton into
each mesh. To morph a mesh in accordance with a
given skeleton position, we chose to use linear skin-
ning (Jacka et al., 2007), since the technique is both
fast and robust, while providing sufficiently good re-
sults. To summarize the implementation, we first as-
sign weights w
i j
to each vertex of the mesh, that char-
acterize how much bone b
j
influences the vertex v
i
.
Let a coordinate system be attached to each bone,
AStatisticalModelforCoupledHumanShapeandMotionSynthesis
229
PCA
matching
scale
Gaussian
model
regression
−3 −2 −1 0 1 2 3 4
−3
−2
−1
0
1
2
3
4
Figure 3: Block diagram of the algorithm; starting from the initial sets of motions (M) and shapes (S), Gaussian model is
built.
then transformation matrix T
j
transforms vertex co-
ordinates from bone coordinate system to world coor-
dinate system. For the new position of the bone,
ˆ
T
j
denotes the new transformation matrix. Then the new
position of the vertex is given by the formula:
ˆv
i
=
K
′
∑
j=1
w
i j
ˆ
T
j
T
−1
j
v
i
,
N
∑
i=1
w
i j
= 1 (2)
where K
′
= K −1 is the number of bones (see Fig.
4). The weights are generated using the solver for the
heat equation, where heat is propagated from each of
the bones (Baran and Popovi
´
c, 2007) until heat equi-
librium is reached, and weights are set equal to the
normalized temperatures.
Figure 4: Alignment of a skeleton and a mesh.
4 APPEARANCE MORPHABLE
MODEL
In this section, we explain our shape-motion model
and its constraints and limitations.
The algorithm for model preparation and training
is given in the Fig. 3. The main idea of our model
is to correlate shape and motion based on semantic
parameters. To achieve better alignment and to avoid
the retargeting problem, we first match and align the
meshes with the motions. A rough match is done
based on semantic parameters, i.e. we create a set
of shape-motion pairs (s
p
, m
q
), such that the values
of the semantic parameters for each pair differ less
than a given threshold ε : P = {(s
p
, m
q
), ∥v(s
p
) −
v(m
q
)∥ < ε} (this procedure corresponds to the first
block in the Fig. 3). In the next step, we morph each
shape s
p
in the way, that its skeleton corresponds ex-
actly to the skeleton of the motion m
q
. To implement
scaling, we modify Eq. (2) by adding a transforma-
tion matrix that represents relative scaling:
ˆv
i
=
K
′
∑
j=1
w
i j
ˆ
T
j
S
j
T
−1
j
v
i
,
N
∑
i=1
w
i j
= 1, (3)
S
j
=
s
j
0 0
0 s
j
0
0 0 s
j
(4)
where s
j
is a scaling factor. After scaling, we fit the
skeleton again using Eq. (1). We iterate between
these two steps several times before the bone lengths
of the newly fitted skelton converge to the desired
values. Since the scaling coefficients, i.e. ratio be-
tween corresponding bone lengths, are in the inter-
val of [0.85, 1.15], it does not affect the realistic look
of the shapes. After scaling, the bone lengths of the
mesh skeleton correspond exactly to those of motion
skeleton.
Since the dimensionality of the data is still high
after this preprocessing step, we first reduce the di-
mensions by performing Principal Component Anal-
ysis (PCA) on both shape and motion coefficients sep-
arately and converting our data into PCA space of
smaller dimensions. PCA transformation consists of
finding orthogonal directions in space (called basis),
corresponding to the maximal variance of the sample.
Then, given a set of vectors x
j
∈ X ⊂ R
l
, N
x
size of
the set X , and the found basis U
x
= [u
1
x
, .. . , u
k
x
], the
original vectors can represented as:
x
j
= U
x
ˆx
j
+ µ(X), j = 1 . . . N
x
(5)
where µ(X) =
1
N
x
∑
N
x
i=1
X
i
is the mean of the set X and
ˆx
j
is a vector of coordinates of x
j
in PCA space, di-
mensionality of ˆx
j
is smaller than the dimensionality
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
230

of x
j
. Then,
ˆx
j
= U
T
x
(x
j
−µ(X)) (6)
is the reverse transformation from ˆx
j
to x
j
.
To apply PCA on our data, we firstly stretch the
matrices, representing shapes and motions, into vec-
tors; therefore we produce two sets: the set of vectors
representing shapes S ⊂ R
3N
and the set of vectors
representing motion M ⊂ R
15K+1
. Than we perform
PCA as described above (see the third block in the Fig
3). We denote the PCA coordinates of smaller dimen-
sionality as ˆm ∈R
ˆ
N
and ˆs ∈R
ˆ
K
accordingly. Dimen-
sionality of the space is chosen in such a way, that
leaves 95% of variance of the sample in both cases.
Now we bind mesh and motion coordinates to learn
a joint Gaussian distribution over a set [ ˆs, ˆm], depend-
ing on the semantic parameters v. In this sense, our
model is close to Active Appearance Models (AAM,
(Cootes et al., 2001)), although in contrast to AAM,
the relation between two sets of PCA coordinates in
our model is probabilistic, i.e. they are not firmly cou-
pled together.
Since each pair has common semantic parameters,
i.e. to each pair of PCA coordinates ˆy = ( ˆs, ˆm) ⊂
ˆ
Y ∈ R
ˆ
N+
ˆ
K
a vector of semantic parameters v is as-
signed, we can now derive control ’handles’ over
our model. For that, we use linear regression in the
space of joint PCA coordinates. Since not all coor-
dinates are correlated with semantic parameters, we
first perform standard correlation significance anal-
ysis and find significant coefficients: I(
ˆ
Y )
r
= {i ∈
[1, . . . ,
ˆ
N +
ˆ
K] : P(ρ(ˆy
i
, v) = 0) < γ}, where ρ( ˆy
i
, v)
is thecorrelation between the i-th coordinate of vector
y and semantic values, γ = 0.05 is p-value for testing
the hypothesis that no correlation exists (Kendall and
Stuart, 1973). We then use coordinates from I(
ˆ
Y )
r
to
build the joint regression model:
ˆy
I(
ˆ
Y )
r
= Θv + ε, (7)
where Θ is a matrix of regression coefficients and
ε ∼ N (0, Σ
I
) is a normally distributed random vari-
able with covariance matrix Σ
I
.
For the rest of the coordinates we assume a joint
Gaussian distribution N (0, Σ
f
), where Σ
f
is the joint
covariance and can be easily estimated from the data.
The full joint model (the construction of the joint
model corresponds to the last two blocks in Fig. 3)
is described by the following equations:
ˆy = µ
ˆ
Y
+
√
Σξ, ξ ∼ N (0, I), (8)
(µ
ˆ
Y
)
i
=
{
(Θv)
k
, i ∈ I(
ˆ
Y ),
0, otherwise
(9)
(a)
(b)
Figure 5: Two examples of conditional sampling of motion:
(a) motion sampled with correlation analysis; (b) motion
sampled without correlation analysis.
Here (Θv)
k
denotes the corresponding coordinate,
obtained from Eq. (7). Without loosing generality,
we can reorder indices in such a way, that indices in
the sets I(
ˆ
S)
r
are put in the beginning, followed by
indices of the elements, which are independent from
semantic parameters. Then, the full covariance matrix
can be written as:
Σ =
(
Σ
I
0
0 Σ
f
)
(10)
Using the proposed model for generating a char-
acter based on semantic parameters is straightfor-
ward: firstly, semantic parameters are chosen to de-
termine the parameters of Gaussian distribution using
Eq (7),(8),(10); then a random point in PCA space is
sampled according to a normal distribution with de-
termined parameters. Finally, the coordinates of the
point are converted into shape-motion space using Eq
(5).
Another useful property of the model is the ability
to animate a given mesh, i.e. create the corresponding
motion, given as well as create a well-fitting appear-
ance, i.e. mesh, based on a motion. Let an input shape
s be given. Firstly, the mesh is transformed in PCA
space. Secondly, we derive a sampling distribution in
the PCA space of ˆs by applying Bayes theorem. We
assume normal distributions and therefore are able to
sample from the conditional distribution to derive the
AStatisticalModelforCoupledHumanShapeandMotionSynthesis
231

mesh coordinates, corresponding to the motion and
vice verse:
P( ˆm|ˆs) =
P( ˆm, ˆs)
P( ˆs).
(11)
Since we assume a parametrized normal distributions
we can write:
µ
ˆm|ˆs
= µ
ˆm
+ Σ
ˆm ˆs
Σ
−1
ˆm ˆm
( ˆs −µ
ˆs
) (12)
Σ
ˆm|ˆs
= Σ
ˆs ˆs
−Σ
ˆs ˆm
Σ
−1
ˆm ˆm
Σ
ˆm ˆs
(13)
ˆm = µ
ˆm|ˆs
+ Σ
ˆm|ˆs
ξ, ξ ∼ N (0, I) (14)
Afterwards, we convert the PCA coordinates of the
generated motion to the original motion space. One
can apply the similar procedure to derive the mesh
coordinates from a given motion.
As mentioned above, we separate coordinates,
correlated with semantic parameters. We do it to
avoid false dependencies between coordinates and to
be able to use free coordinates to our model to in-
troduce more variability into the generation process.
To show the importance of separating correlated co-
ordinates, we perform the following experiment: we
divide the databases into two disjoint parts - test and
train parts, train our model using train parts of each
of the databases and then perform motion sampling
conditioned on a mesh from the test part of the mesh
database using the model with correlation analysis
and without correlation analysis. As can be seen in
the Fig. 5, the model that uses all coordinates for
the regression (i.e. the model trained without correla-
tion analysis) fails to generate suitable motion, while
the model with correlation analysis produces realistic
motion. We explain that by the fact, that coordinates
of the mesh from the test set possibly are far from
the coordinates of the meshes in train set, and there-
fore false dependencies introduced by regression on
all coordinates have strong influence and produce im-
plausible results.
5 EVALUATION
As stated above, our model allows to generate
highly realistic shape-motion correlation with rela-
tively small afford. In this section, we evaluate sim-
ulated sequences in terms of motion fidelity, and also
provide quantitative evaluation to show how our ap-
proach allows to avoid the motion retargeting prob-
lem.
There is a number of methods for visual fidelity
evaluation proposed in the literature. They can be di-
vided into interrogation approaches and automatic ap-
proaches.
Interrogation-based approaches can be applied on
very different problems. In (Reitsma and Pollard,
2003), experiments with human observers were con-
ducted to determine the sensitivity of human percep-
tion to physical errors in motions and (Hodgins et al.,
1998) investigated, which types of anomalies added
to the motion disturb human perception the most. In
(Pra
ˇ
z
´
ak and O’Sullivan, 2011) and (McDonnell et al.,
2008) human crowd variety was investigated and in-
fluence of either motion or shape clones on the whole
crowd perception was investigated.
As an example of the automated motion evalua-
tion approaches, (Ren et al., 2005) proposed and eval-
uated automated data-driven method for assessing un-
naturalness of the human motion; in (Ahmed, 2004)
motion is evaluated in terms of feet sliding and gen-
eral smoothness, while in (Jang et al., 2008) phys-
ical plausibility of motion was evaluated. Unfortu-
nately, as also mentioned by (Ren et al., 2005), these
approaches depend a lot on the type of distortion, ap-
plied to motion, and therefore are directed on the eval-
uation of a specific type of motion generation.
Interrogation-based approaches provide more
general results and are more reliable and more suit-
able for our goal.
Therefore, we performed two experiments de-
signed as questionnaires and one additional experi-
ment for quantitative evaluation. 13 male and 10 fe-
male subjects took part in our experiment. The exper-
imental setup is described below.
5.1 Interrogation-based Evaluation
Experiment 1. In the first experiment, we asked
the participants to compare two animations, one of
which was generated using the model and the second
one was generated by choosing motion and mesh ran-
domly from our databases. We prepared 3 pairs of
videos of 10 s. length. The parameters of the gen-
erated (or selected) characters are given in the Table
1. To diminish bias due to greater attractiveness of
one figure in comparison to another, we chose appear-
ances, that have approximately the same semantic pa-
rameters, e.g. compared two fat humans, or two thin
humans etc.
The perspective and surroundings for the ani-
mated figures, as well as textures of the figures were
the same. The participants were asked to indicate,
which animation from the pairs looked more realis-
tic; they also had the opportunity to state, that both
animations looked equally bad or equally good. The
results of the experiment are summarized in the Table
2.
As the results show, the mesh-to-motion fit de-
livers in general better results then just combining
mesh and motion without taking into account param-
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
232
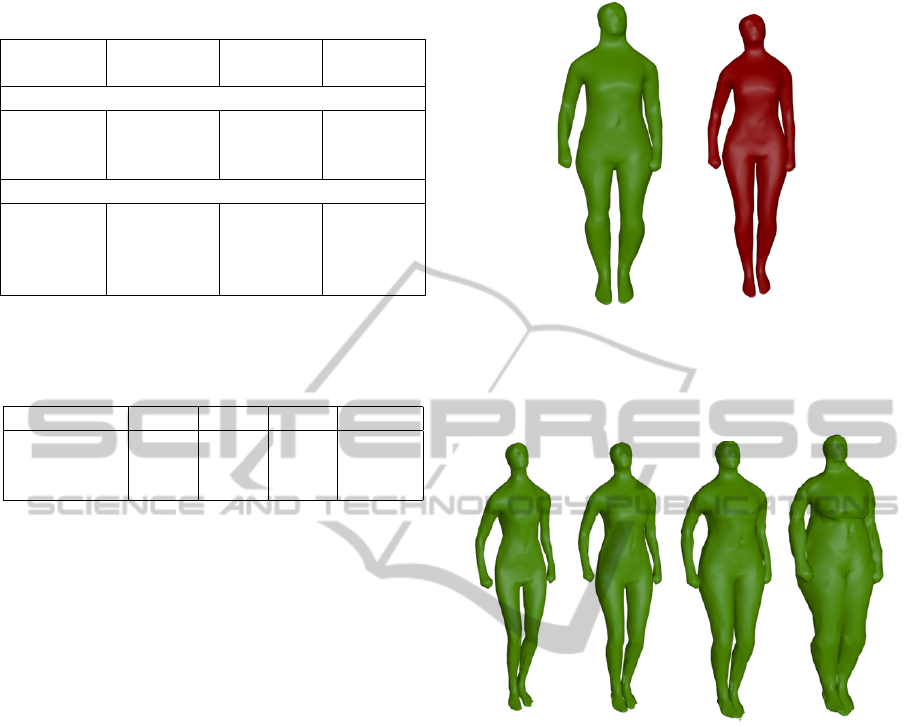
Table 1: Semantic parameters (weight in kg., height in cm.)
of the samples used in the experiments.
our model selected
mesh
selected
motion
Experiment 1
pair 1 (40, 169) (53, 173) (86, 176)
pair 2 (70, 155) (44.7, 150) (75.2, 186)
pair 3 (110, 170) (120, 176) (49, 168)
Experiment 2
question 1 (90, 176) (102, 176) (86.3, 176)
question 2 (45, 169) (49, 169) (49.5168)
question 3 (77.9, 179) (77.9, 176) (77.9, 181)
question 4 (75, 178) (75.6, 178) (74.5, 179)
Table 2: Percentage of the participants, that accepted the
sequence generated with our model as more realistic, less
realistic and percentage of people, having difficulty to eval-
uate one of the motions as more natural.
pair 1 pair 2 pair 3 average
positive (%) 65.00 30.00 80.00 58.33
neutral (%) 15.00 15.00 10.00 13.33
negative (%) 20.00 55.00 10.00 28.33
eters of combined mesh and motion. We explain fail-
ure in the second pair of sequences due to generally
lesser attractiveness of the appearance sampled from
the model (see Fig. 6). In general, we observed, that
mismatch between mesh and motion due to difference
in weight is a lot easier to detect then mismatch due
to difference in height, because in the latter case pro-
portions of the person, unless some extreme cases are
taken (e.g. a six-year child and a tall adult) are the
same and therefore motion can fit quite well. Some
more examples of subjects, sampled using our model,
are given in the Fig 7.
Taking into account, that during artificial charac-
ter animation it is usually difficult to find real motion
data that fits exactly to the animated shape, our ap-
proach is beneficial in terms of delivered result.
Experiment 2. In the second experiment, we asked
our participants to evaluate several sets of videos. In
each set, four videos were presented. The videos in
each set were produced as follows:
• A
1
: an animation was generated by matching
mesh and motion based on semantic parameters;
• A
2
: an animation was generated by sampling
mesh and motion from the model with the same
semantic parameters;
• A
3
: a mesh was taken from the database of meshes
and a motion was sampled from our model given
the mesh;
• A
4
: an animation, where a motion was taken from
(a) (b)
Figure 6: Shapes used in the second pair of sequences in ex-
periment 1 for comparison of visual fidelity (a) mesh sam-
pled from the model (b) mesh from the original database.
(a) weight:40kg,
height:169cm
(b) weight:61kg,
height:171cm
(c) weight:77kg,
height:178cm
(d) weight:110kg,
height:170cm
Figure 7: Examples of simulated characters.
the database of motion and a mesh was sampled
from our model given the motion.
The parameters of the samples are given in Table 1.
The participants should grade each video with marks
from 1 to 4, where 1 means very visually plausible
and 4 mean completely unrealistic. In Table 3, the
results are given in the form of percentage of partic-
ipants, that evaluated sequences with 1, 2, 3 or 4 re-
spectively.
As the results show, that our model produces
slightly better results as match of semantic parame-
ters, which is a doos result given that the two data
bases were only matched via semantic parameters
during training.The second most realistic animation
is delivered by motion sampling, conditioned on the
mesh, while appearance sampling (i.e. mesh sam-
pling) based on motion generates the same or even
slightly lower results, then semantic matching. We
AStatisticalModelforCoupledHumanShapeandMotionSynthesis
233

Table 3: Percentage of the participants, given marks from
1 to 4 and mean note for each algorithm. The notes can
vary in the interval [1, 4], where 1 means very realistic, and
4 means not visually plausible.
alg. 1 2 3 4 average
note
A
1
15.00 30.00 42.50 12.50 2.52
A
2
33.75 51.25 13.75 1.25 1.82
A
3
20.00 40.00 28.75 11.25 2.31
A
4
18.75 25.00 33.75 22.50 2.60
attribute this to the fact that motion still does not pro-
vide enough information to sample appearance accu-
rately.
We explain the superiority of our sampling meth-
ods with several arguments: firstly, mesh and mo-
tion sampled with our model are aligned better to
each other, and secondly, due to smoothing on the
PCA stage, small artifacts, appearing occasionally in
matched sequences, are smoothed away, and therefore
visually plausible result can be produced.
5.2 Quantitative Evaluation
There exist several approaches to solve the motion re-
targeting problem, and none of them is perfect. How-
ever, we can avoid this problem by generating mesh
and motion simultaneously. We evaluate the mesh-
motion fit by comparing bone lengths of the mesh
skeleton b
s
j
and corresponding bone lengths of the
motion skeleton b
m
j
in terms of amount of scaling
needed:
s
j
= 1 −
b
s
j
b
m
j
(15)
Here j corresponds to a body part and s
j
denotes
the amount of scaling required to fit mesh to motion.
For the motion and mesh from the same person, i.e.
when no scaling is required, the amount of scaling
equals zero. As shown in the Figure 8, the model cap-
tures dependencies in bone lengths in mesh with bone
lengths in motion and allows to generate pairs of mesh
and motion already scaled properly, so that no scaling
is required afterwards. We also evaluate mesh-motion
fit in terms of conditional mesh sampling, when mo-
tion is given, and conditional motion sampling, when
mesh is given. We create pairs from the real data us-
ing semantic matching and for the same range of se-
mantic parameters we sample pairs from the model.
The results (Fig. 8) confirm, that mesh and motion in
the pairs, sampled from the model, are already prop-
erly aligned to each other.
hand forearm shoulder torco crus thigh pelvis
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
s is scale factor for the bones
model−gen. data, on sem. param
model−gen. data, cond. on mesh
model−gen. data, cond. on motion
sem.−matched real data
Figure 8: The mean amount of scaling required for each of
the body parts; green color corresponds to the pairs sampled
from the model, red color corresponds to the matched pairs.
When no scaling is required, the amount of scaling equals
0.
5.3 Using the Model in Crowd
Simulation
As mentioned above, we also propose to use the
model for automatic character appearance and mo-
tion simulation of crowds. We leave out of scope of
this paper the question of crowd behavior simulation,
since it is an active area of research and numerous ap-
proaches exist (see, for example, (Guy et al., 2010),
(Narain et al., 2009)). By controlling the distribution
of the semantic parameters, it is possible to generate
a set of character meshes, that is specific to the scene.
In our example, we generate the crowd by randomly
placing sampled characters in space. For creating the
crowd in Fig. 9 and 10, we used a uniform distribution
of the semantic parameters weight and height. How-
ever, one can consider more advanced ways of setting
semantic parameters, if some specific distribution of
shapes and motions is required.
More demonstrations are provided in the supple-
mentary material.
6 FUTURE WORK
As our experiments have shown, there are several lim-
itations of our model. First of all, our model was ap-
plied to a cyclical motion, so its extension to arbi-
trary type of motion can represent some difficulties.
Secondly, the model can be used to generate samples
based on semantic parameters, when the semantic pa-
rameters are not very far from the range of the param-
eters used for training. However, when it is not the
case, produced results can look unrealistic. We hope,
that increasing size and variability of the datatbases
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
234

Figure 9: Example of crowd generation with semantic parameters weight and height uniformly distributed on [40, 70] and
[150, 180] accordingly. The animation itself can be viewed in additional materials.
Figure 10: Example of crowd generation with semantic parameters weight and height uniformly distributed on [50, 100] and
[150, 200] accordingly. The animation itself can be viewed in additional materials.
will help to generate characters with a wider range of
semantic parameters.
Therefore, in future we are planning to extend
our work on more complex motions, as well as
achieve better mesh-motion fitting in the model train-
ing phase. More complex motions should firstly be
aligned using techniques such as time warping (Hsu
et al., 2007) and then the similar procedures as in
(Troje, 2002) should be applied to produce vector-
based representation of motions, suitable for analysis.
Another interesting topic is the use of more ad-
vanced stochastic models for mesh-motion coordi-
nates coupling to be able to capture non-linear depen-
dencies.
7 CONCLUSIONS
In our work, we proposed a parametrized model com-
bining shape and motion, that can be applied to gener-
ate realistic characters together with appropriate mo-
tion. While providing enough variability, the model
allows tight control over the generation process with
the help of semantic parameters, and has a probabilis-
tic formulation.
Although the usage of two independent databases
can be seen as a weakness of our approach, we want
to stress that the method was suggested to find de-
pendencies in the initially unrelated databases and use
them to bridge these databases. Such an approach can
be advantageous when it is not possible or difficult to
collect motion and shape data together from the same
subjects.
Our model can be used to generate completely
new meshes and motion, as well as to generate a spe-
cific motion for a given mesh or a specific shape using
an existing motion.
We also evaluated our model in three experiments,
that showed superiority of the proposed model in
terms of visual plausibility of created samples in com-
parison to simple matching based on semantic param-
eters. We furthermore avoid the retargeting problem,
since our model already contains necessary depen-
dencies in it.
The model can be easily extended to bigger
datasets, since all the algorithms used here in general
are computationally inexpensive.
Possible applications of our model include ani-
mating existing characters, creating appearance based
on motion, as well as creating a visually plausible
crowd.
ACKNOWLEDGEMENTS
We would like to thank Prof D. Fleet for the very help-
ful discussions and good advice.
AStatisticalModelforCoupledHumanShapeandMotionSynthesis
235

REFERENCES
Ahmed, A. A. H. (2004). Parametric synthesis of human
animation.
Anguelov, D., Srinivasan, P., Koller, D., Thrun, S., Rodgers,
J., and Davis, J. (2005). Scape: shape completion and
animation of people. ACM Trans. Graph, 24:408–416.
Baran, I. and Popovi
´
c, J. (2007). Automatic rigging and
animation of 3d characters. In ACM SIGGRAPH 2007
papers, SIGGRAPH ’07, New York, NY, USA. ACM.
Brand, M. and Hertzmann, A. (2000). Style machines.
In Proceedings of the 27th annual conference on
Computer graphics and interactive techniques, SIG-
GRAPH ’00, pages 183–192, New York, NY, USA.
ACM Press/Addison-Wesley Publishing Co.
Cootes, T. F., Edwards, G. J., and Taylor, C. J. (2001). Ac-
tive appearance models. IEEE Trans. Pattern Anal.
Mach. Intell., 23(6):681–685.
da Silva, M., Abe, Y., and Popovi
´
c, J. (2008). Interactive
simulation of stylized human locomotion. In ACM
SIGGRAPH 2008 papers, SIGGRAPH ’08, pages
82:1–82:10, New York, NY, USA. ACM.
Guy, S. J., Chhugani, J., Curtis, S., Dubey, P., Lin, M., and
Manocha, D. (2010). Pledestrians: a least-effort ap-
proach to crowd simulation. In Proceedings of the
2010 ACM SIGGRAPH/Eurographics Symposium on
Computer Animation, SCA ’10, pages 119–128, Aire-
la-Ville, Switzerland, Switzerland. Eurographics As-
sociation.
Hasler, N., Stoll, C., Sunkel, M., Rosenhahn, B., p. Seidel,
H., and Informatik, M. (2009). A statistical model of
human pose and body shape. computer graphics fo-
rum28.
Hodgins, J. K., O’Brien, J. F., and Tumblin, J. (1998).
Perception of human motion with different geomet-
ric models. IEEE Transactions on Visualization and
Computer Graphics, 4(4):101–113.
Hsu, E., da Silva, M., and Popovi
´
c, J. (2007). Guided time
warping for motion editing. In Proceedings of the
2007 ACM SIGGRAPH/Eurographics symposium on
Computer animation, SCA ’07, pages 45–52, Aire-la-
Ville, Switzerland, Switzerland. Eurographics Associ-
ation.
Jacka, D., Merry, B., and Reid, A. (2007). A comparison of
linear skinning techniques for character animation. In
In Afrigraph, pages 177–186. ACM.
Jang, W.-S., Lee, W.-K., Lee, I.-K., and Lee, J. (2008). En-
riching a motion database by analogous combination
of partial human motions. Vis. Comput., 24(4):271–
280.
Kendall, G. and Stuart, A. (1973). The Advanced Theory of
Statistics. Vol.2: Inference and: Relationsship. Grif-
fin.
Lee, Y., Lee, S. J., and Popovi
´
c, Z. (2009). Compact charac-
ter controllers. In ACM SIGGRAPH Asia 2009 papers,
SIGGRAPH Asia ’09, pages 169:1–169:8, New York,
NY, USA. ACM.
Li, Y., Wang, Y. L. T., and yeung Shum, H. (2002). Mo-
tion texture: A two-level statistical model for charac-
ter motion synthesis. In ACM Transactions on Graph-
ics, pages 465–472.
Liu, C. K., Hertzmann, A., and Popovic, Z. (2005). Learn-
ing physics-based motion style with nonlinear inverse
optimization. ACM Trans. Graph, 24:1071–1081.
McDonnell, R., Larkin, M., Dobbyn, S., Collins, S., and
O’Sullivan, C. (2008). Clone attack! perception of
crowd variety. In ACM SIGGRAPH 2008 papers, SIG-
GRAPH ’08, pages 26:1–26:8, New York, NY, USA.
ACM.
Narain, R., Golas, A., Curtis, S., and Lin, M. C. (2009). Ag-
gregate dynamics for dense crowd simulation. In ACM
SIGGRAPH Asia 2009 papers, SIGGRAPH Asia ’09,
pages 122:1–122:8, New York, NY, USA. ACM.
Popovic, Z. and Witkin, A. P. (1999). Physically based mo-
tion transformation. In SIGGRAPH, pages 11–20.
Pra
ˇ
z
´
ak, M. and O’Sullivan, C. (2011). Perceiving human
motion variety. In Proceedings of the ACM SIG-
GRAPH Symposium on Applied Perception in Graph-
ics and Visualization, APGV ’11, pages 87–92, New
York, NY, USA. ACM.
Reitsma, P. S. A. and Pollard, N. S. (2003). Per-
ceptual metrics for character animation: sen-
sitivity to errors in ballistic motion. In ACM
SIGGRAPH 2003 Papers, pages 537–542.
http://www.odysci.com/article/1010112995491572.
Ren, L., Patrick, A., Efros, A. A., Hodgins, J. K., and Rehg,
J. M. (2005). A data-driven approach to quantifying
natural human motion. ACM Trans. Graph, 24:1090–
1097.
Sidenbladh, H., Black, M. J., and Sigal, L. (2002). Implicit
probabilistic models of human motion for synthesis
and tracking. In In European Conference on Computer
Vision, pages 784–800.
Sok, K. W., Kim, M., and Lee, J. (2007). Simulating
biped behaviors from human motion data. ACM Trans.
Graph., 26(3).
Troje, N. F. (2002). Decomposing biological motion: A
framework for analysis and synthesis of human gait
patterns. In Journal of Vision, volume 2, pages 371–
387.
Wang, J. M., Fleet, D. J., and Hertzmann, A. (2008). Gaus-
sian process dynamical models for human motion.
IEEE Trans. Pattern Anal. Mach. Intell., 30(2):283–
298.
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
236
