
How to Use Information Theory for Image Inpainting and Blind Spot
Filling-in?
J. M. Berthomm
´
e, T. Chateau and M. Dhome
Institut Pascal - UMR 6602, Universit
´
e Blaise Pascal, 24 Avenue des Landais, 63177 Aubi
`
ere Cedex, France
Keywords:
Image Inpainting, Information Theory, Blind Spot.
Abstract:
This paper shows how information theory can both drive the digital image inpainting process and the optical
illusion due to the blind spot. The defended position is that the missing information is padded by the “most
probable information around” via a simple filling-in scheme. Thus the proposed algorithm aims to keep the
entropy constant. It cares not to create too much novelty as well as not to destroy too much information.
For this, the image is broken down into regular squares in order to build a dictionary of unique words and to
estimate the entropy. Then the occluded region is completed, word by word and layer by layer, by picking
the element which respects the existing image, which minimizes the entropy deviation if there are several
candidates, and which limits its potential increase in the case where no compatible word exists and where a
new one must be introduced.
1 INTRODUCTION
The eye’s blind spot has been discovered in 1660 by
Edme Mariotte, a French physicist, whose experi-
ment seemed magical when it was first presented to
Louis XIV ’s court. Today, despite three-and-a-half
centuries of progress, this demonstration still resists
interpretation.
From the 19
th
century until now naturalists then
neuroscientists have remarkably well investigated the
visual system. However, despite tons of observations
they do not fully understand yet its functioning. Brain
modelling remains a real challenge.
On the other hand, the relatively recent commu-
nity of computer vision, clearly based on hard sci-
ence, has a lot to do to solve its own problems, e.g.
segmentation, 3D reconstruction or tracking. It looks
for good algorithms, not laws. As a result it has regu-
larly claimed that it has nothing to do with medicine,
perceived as too experimental.
Whatever these clich
´
es, some pieces seem to
match. Image Inpainting experiments can precisely
simulate the illusion of the blind spot and more funda-
mentally Information Theory can simply explain the
principle underlying the phenomenon.
2 THE BLIND SPOT
2.1 Demonstration
Let us start by showing an experiment that ophtal-
mologists know well. Look at the top part (a) of
figure 1 with the big dot and the cross. Close your
right eye and force your left eye to stare at the cross
slightly sidelongly. Slowly move your head closer
to the screen. When the image of the dot hits your
blind spot it disappears. Note that as soon as you let
your left eye directly look at the dot it immediatly
reappears. Then use the same distance in case (b).
The hole of the horizontal line is now completed so
that it appears continuous. These two examples have
demonstrated the existence of your blind spot.
2.2 Partial explanation
Neuroscientists half understand the phenomenon.
They see why information is missing but not why it
is completed. As shown in figure 2 it occurs where
the optic nerve leaves the eye. The axons of the retinal
ganglion cells concentrate at one point and go through
the retina, preventing any presence of photoreceptors.
In human beings the blind spot is large, about 4
o
of
the view field. It is located at slightly different angles
in each eye, probably to facilitate their mutual filling.
Finally, some invertebrates like cephalopods do not
97
Berthommé J., Chateau T. and Dhome M..
How to use Information Theory for Image Inpainting and Blind Spot Filling-in?.
DOI: 10.5220/0004216300970100
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 97-100
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Two experiments that demonstrate the existence of the blind spot. To make the black dot in (a) or the white hole in
(b) disappear, close your right eye and force your left eye to look at the cross with a slight angle, then slowly move your head
back and forth at about 25 cm from the screen.
have a blind spot. Their nerve fibers route behind the
retina and do not block light.
Figure 2: In the eyes of the vertebrates, the nerve fibers
route before the retina, blocking some light and creating a
blind spot where the fibers pass through the retina and out
of the eye. (i) human retinography, (ii) diagram of human
eye, and (iii) photoreceptor density highlight the blind spot.
2.3 Emulation
We are almost always unaware of our natural blind
spots. So how are they naturally filled in? One radi-
cal solution would be to experiment with a conscious
patient full of instruments in his eye and his cortex.
To the best of our knowledge, this is not yet feasible.
Beyond ethics, there are still technical issues.
Other people have made the parallel with Image
Processing and tried to model the phenomenon in or-
der to emulate the filling-in process. That is the per-
spective we have adopted. But, from what we read,
and whatever the community, they have talked about
“visual interpolation” (Durgin, 1995) and have ap-
plied variational approaches (Liu et al., 2007) (Arias
et al., 2011) to constrained Partial Differential Equa-
tion (Satoh, 2011) (PDE) problems. We contest this
interpretation. Why? To make it short, simply be-
cause interpolation can fast create unexpected things,
i.e. disorder, in other words entropy.
In the following section this idea is reformulated
within the Information Theory framework. Based
on that principle we describe an inpainting algorithm
that aims to keep the entropy constant. It can not
only reproduce the blind spot experiments (a) and
(b) but also complete any damaged image. We have
provided MATLAB implementations able to inpaint
binary, grayscale or RGB images of any bit depth
at: http://wwwlasmea.univ-bpclermont.fr/Personnel/
Jean-Marc.Berthomme/.
3 ENTROPY INPAINTING
Inpainting is the process that replaces undesired in-
formation by contextual information without altering
the global consistency of the signal. It is not necessar-
ily restricted to image restoration as it can also apply
to sounds or videos. In all cases it relies on digital
signals.
3.1 Formulation
Inpainting should not make unexpected things arise
or disappear. So, in the Information Theory frame-
work, we state that: “Inpainting must neither create
nor destroy information“. By defining X
u
, the un-
known part of an image, and X
k
, its known part, the
ideal goal is to get: H(X
u
,X
k
) = H(X
k
), which is
equivalent to (MacKay, 2003): H(X
u
/X
k
) = 0. Thus
the proposed algorithm aims to keep the entropy of
the growing known region constant. As long as there
are n
u
unknown bits there are 2
n
u
possible subimages
so H(X
u
) = n
u
bits. Concerning H(X
k
) its estimation
requires to divide X
k
into pieces in order to specify
a dictionary D and therefore propagate the filling-in
process. Anyway, inpainting can be reformulated as
an optimization problem looking for an unknown sig-
nal X
∗
u
and an unknown dictionary D
∗
so that:
minimize |H
D
(X
u
,X
k
) − H
D
(X
k
)|
subject to X
k
3.2 Building the Dictionary &
Estimating the Entropy
When the unwanted information is removed from the
damaged image the method first breaks down the re-
maining known region. The partition possibilities are
huge, from blocks of 1 x 1 pixels to the size of the
image itself. Whatever the choice, the goal is to fetch
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
98

the redundant patterns, so all the shapes are not rel-
evant. Note that 1 x 1 cutting makes an exception
because it loses the spatial consistency, so it is never
used. Similarly, a sliding windowing is applied to the
image in order not to miss any stitching between the
patches. Though precise, this exhaustive enumeration
is expensive. So, to shorten it, exclusive or even ran-
dom windowing strategies could be considered. The
counting of the broken blocks leads to the building of
a dictionary D. It is composed of unique words asso-
ciated with their frequencies p
i
. These latter allow to
estimate the entropy H of the image.
3.3 Filling in the Selection
Based on such a dictionary, any missing pixel can be
replaced by looking for the patch - or the word fol-
lowing the point of view - that best fits the selection
around. Three cases can occur. There can be one, sev-
eral or no compatible words in the dictionary. Note
that the compatibility is checked on the known pixels
of the selection. It is calculated with the logic func-
tions NOT, XOR and AND as each piece of image is
stored as a set of Boolean. So, if there is only one
word, it is always taken. If there are several, the se-
lected one must minimize the absolute entropy devia-
tion. Finally, if no compatible word exists a new one
is created. It does not challenge the known part of the
selection. It only retains the consensus within the dic-
tionary concerning the unknown part. To conclude,
the whole process is summarized in algorithm 1 be-
low.
4 EXPERIMENTAL RESULTS
Our implementation has investigated dictionaries of
square patches. It can emulate the blind spot com-
pletion described in section 2 with an image of size
25x100 and patches of any size between 2x2 to 25x25
in this case. The results, grouped in figure 3 below,
correspond to a filling in with words of size 3x3.
We have also explored characteristic patterns like
crosses in order to see how to constrain the novelty
creation. This work has started with binary images
and was then extended to grayscale and RGB images
of any bit depth. Random images have equally pro-
cured a deep reflection. We first wanted to minimize
the entropy, not its absolute deviation. So we encoded
redundancy and thus destroyed information. As ran-
dom images are already at maximum entropy, regard-
less of their breaking down, we must maintain their
entropy constant to be able to reproduce their pattern.
Algorithm 1: Entropy Inpainting Algorithm.
input : unknown signal X
u
and known signal
X
k
such that X
u
∩ X
k
= ∅
output: X
u
completed so that
H
D
(X
u
,X
k
) ≈ H
D
(X
k
)
build a dictionary D from X
k
and calculate
H(X
u
) and H(X
k
);
while X
u
is not completed do
define an overlapping layer L between X
u
and X
k
;
while L is not completed do
define a selection S inside L ;
find the compatible words between S
and D;
if there is one candidate then
select this word;
else if there are several candidates then
select the word which minimizes
the absolute entropy deviation;
else // there is no candidate
create a new word compatible with
S and D;
end
fill in S with the returned word;
update X
u
, X
k
, D and recalculate H(X
u
)
and H(X
k
);
end
end
Finally we have tried to inpaint natural images taken
from the benchmark dataset proposed by (Kawai et
al., 2009) at: http://yokoya.naist.jp/research/ inpaint-
ing. Our RMSE values compare the inpainted image
to the original one within the completed region only.
They are not relevant to highlight the image global
consistency but they are good to compare the inpaint-
ing methods. We readily acknowledge that our imple-
mentation could highly be improved compared to the
others. Clearly we do not manage edges and complex
textures.
5 CONCLUSIONS
This paper has underscored the fact that Information
Theory can simply formulate the inpainting process
and precisely emulate the blind spot filling-in. It has
emphasized that the goal of inpainting is neither to
create nor to destroy information. Thus the inpaint-
ing process was reformulated within the Information
Theory framework under the form of an optimiza-
tion problem looking for both a dictionary and an un-
known signal. It aims to keep the entropy of the grow-
HowtouseInformationTheoryforImageInpaintingandBlindSpotFilling-in?
99
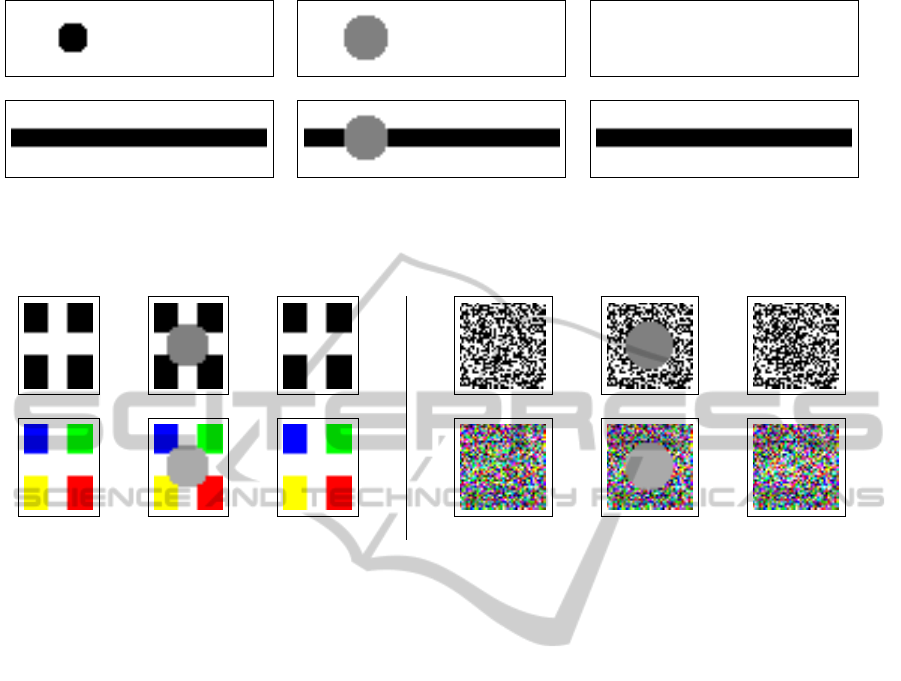
(1a) (2a) (3a)
(1b) (2b) (3b)
Figure 3: Entropy inpainting with 3x3 patches emulating the blind spot filling-in. (1) denotes the original images, (2) the
damaged images with the same gray cache, and (3) the final inpainted images. (a) and (b) refer to the experiments described
in section 2.
(1c) (2c) (3c)
(1d) (2d) (3d)
(1e) (2e) (3e)
(1f) (2f) (3f)
Figure 4: Entropy inpainting with 3x3 patches recovering characteristic patterns on binary and RGB images. (1) denotes the
original images, (2) the damaged images with the gray cache, and (3) the final inpainted images. (c) and (d) cases are sensitive
to the creation of information. (e) and (f) cases are sensitive to the destruction of information.
ing known signal constant. For that, an example of
entropy inpainting algorithm has been proposed.
The provided implementation has simulated the
described optical illusions due to the blind spot ex-
periments. It can equally inpaint binary, grayscale or
RGB images of any bit depth. However it is far for
being optimal. This is mainly due to the exclusive use
of fixed size square patches in the dictionary. This
can be greatly improved by removing almost all the
constraints on the shape of the words.
Last but not least, we are convinced that it is worth
modelling simple optical illusions to push the theory
to its limits and to better understand the perception
process. Many things remain unclear and there are
still a lot of things to do and to learn.
REFERENCES
Arias, P., Facciolo, G., Caselles, V., and Sapiro, G. (2011).
A variational framework for exemplar-based image in-
painting. International journal of computer vision,
93(3):319–347.
Durgin, F. H. (1995). On the filling in of the visual blind
spot: some rules of thumb. Perception, 24:827–840.
Kawai, N., Sato, T., and Yokoya, N. (2009). Image inpaint-
ing considering brightness change and spatial locality
of textures and its evaluation. Advances in Image and
Video Technology, pages 271–282.
Liu, D., Sun, X., Wu, F., Li, S., and Zhang, Y. (2007). Image
compression with edge-based inpainting. Circuits and
Systems for Video Technology, IEEE Transactions on,
17(10):1273–1287.
MacKay, D. (2003). Information Theory, Inference, and
Learning Algorithms. Cambridge University Press.
Satoh, S. (2011). Computational identity between digital
image inpainting and filling-in process at the blind
spot. Neural Computing & Applications, pages 1–9.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
100
