
Gesture Recognition using Skeleton Data with Weighted Dynamic Time
Warping
Sait Celebi
1
, Ali S. Aydin
2
, Talha T. Temiz
2
and Tarik Arici
2
1
Graduate School of Natural and Applied Sciences, Istanbul Sehir University, Istanbul, Turkey
2
College of Engineering and Natural Sciences, Department of Electrical Engineering,
Istanbul Sehir University, Istanbul, Turkey
Keywords:
Gesture Recognition, Dynamic Time Warping, Kinect.
Abstract:
With Microsoft’s launch of Kinect in 2010, and release of Kinect SDK in 2011, numerous applications and
research projects exploring new ways in human-computer interaction have been enabled. Gesture recognition
is a technology often used in human-computer interaction applications. Dynamic time warping (DTW) is a
template matching algorithm and is one of the techniques used in gesture recognition. To recognize a gesture,
DTW warps a time sequence of joint positions to reference time sequences and produces a similarity value.
However, all body joints are not equally important in computing the similarity of two sequences. We propose
a weighted DTW method that weights joints by optimizing a discriminant ratio. Finally, we demonstrate the
recognition performance of our proposed weighted DTW with respect to the conventional DTW and state-of-
the-art.
1 INTRODUCTION
Interacting with computers using human motion is
commonly employed in human-computer interaction
(HCI) applications. One way to incorporate human
motion into HCI applications is to use a predefined
set of human joint motions i.e., gestures. Gesture
recognition has been an active research area (Liang
and Ouhyoung, 1998; D. Gehrig and Schultz, 2009;
Reyes et al., 2011; Wilson and Bobick, 1999), and
involves state-of-the-art machine learning techniques
and capability to work reliably in different environ-
ments. A variety of methods have been proposed for
gesture recognition, ranging from the use of Dynamic
Time Warping (Reyes et al., 2011) to Hidden Markov
Models (D. Gehrig and Schultz, 2009). DTW mea-
sures similarity between two time sequences which
might be obtained by sampling a source with vary-
ing sampling rates or by recording the same phe-
nomenon occurring with varying speeds (Wikipedia,
2012). For example, DTW is used in speech recogni-
tion to warp speech in time to be able to cope with dif-
ferent speaking speeds (Amin and Mahmood, 2008;
Myers, 1980). DTW is also used in data mining and
information retrieval to deal with time-dependent data
(Rath and Manmatha, 2003; Adams et al., 2004). In
gesture recognition, DTW time-warps an observed
motion sequence of body joints to pre-stored gesture
sequences (Rekha et al., 2011; Wenjun et al., 2010).
The conventional DTW algorithm is basically a
dynamic programming algorithm, which uses a recur-
sive update of DTW cost by adding the distance be-
tween mapped elements of the two sequences at each
recursion step. The distance between two elements
is oftentimes the Euclidean distance, which gives
equal weights to all dimensions of a sequence sam-
ple. However, depending on the problem a weighted
distance might perform better in assessing the similar-
ity between a test sequence and a reference sequence.
For example in a typical gesture recognition problem,
body joints used in a gesture can vary from gesture
class to gesture class. Hence, not all joints are equally
important in recognizing a gesture.
We propose a weighted DTW algorithm that uses
a weighted distance in the cost computation. The
weights are chosen so as to maximize discriminant
ratio based on DTW costs. The weights are ob-
tained from a parametric model which depends on
how active a joint is in a gesture class. The model
parameter is optimized by maximizing the discrimi-
nant ratio. By doing so, some joints will be weighted
up and some joints will be weighted down to max-
imize between-class variance and minimize within-
class variance. As a result, irrelevant joints of a ges-
620
Celebi S., Aydin A., Temiz T. and Arici T..
Gesture Recognition using Skeleton Data with Weighted Dynamic Time Warping.
DOI: 10.5220/0004217606200625
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 620-625
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
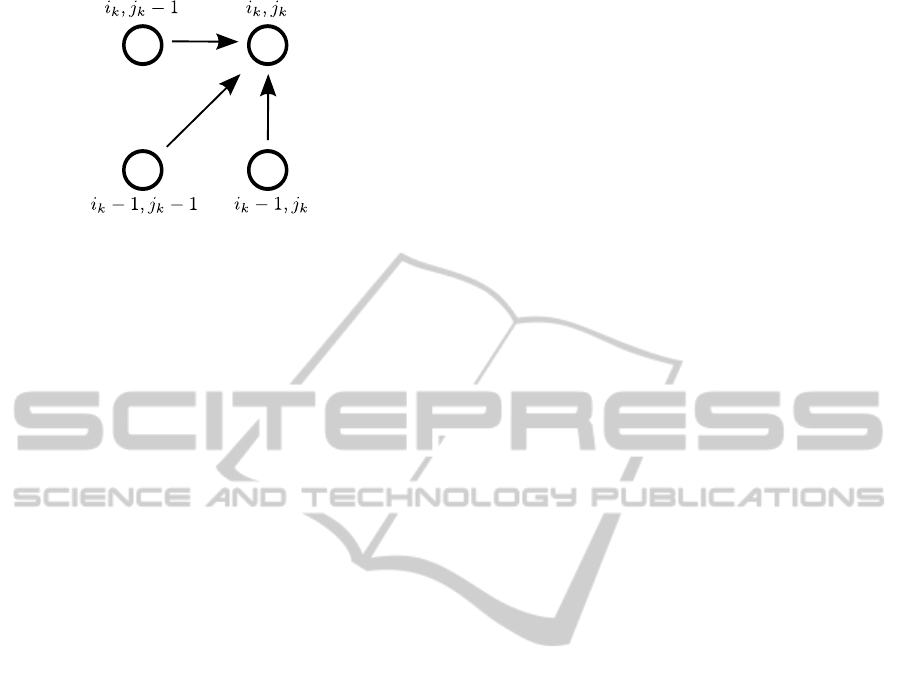
Figure 1: Predecessor nodes used in Bellman’s principle.
ture class (i.e., parts that are not involved in a gesture
class) will contribute to its DTW cost to a lesser ex-
tent, but at the same time between-class variances will
be kept large.
Our system first extracts body-joint features from
a set of skeleton data that consists of six joint posi-
tions, which are left and right hands, wrists and an-
kles. We have observed that the gestures in our train-
ing set, which have quite different motion patterns,
require the use of all or a subset of these six joints
only. These features obtained from skeleton frames
are accumulated over time and used to recognize ges-
tures by matching them with pre-stored reference se-
quences. The matching is then performed by assign-
ing a test sequence to a reference sequence with the
minimum DTW cost. DTW aligns two sequences in
time by speeding up or speeding down a sequence in
time.
2 BACKGROUND
HMMs are statistical models for sequential data
(Baum et al., 1970; Baum, 1972), and therefore can
be used in gesture recognition (D. Gehrig and Schultz,
2009) (Starner and Pentland, 1996). The states of an
HMM are hidden and state transition probabilities are
to be learnt from the training data. However, defining
states for gestures is not an easy task since gestures
can be formed by a complex interaction of different
joints. Also, learning the model parameters i.e., tran-
sition probabilities, requires large training sets, which
may not always be available. On the other hand, DTW
does not require training but needs good reference se-
quences to align with. Next, we present a more de-
tailed discussion on DTW.
2.1 Dynamic Time Warping
DTW is a template matching algorithm to find the best
match for a test pattern out of the reference patterns,
where the patterns are represented as a time sequence
of measurements or features obtained from measure-
ments.
Let r(i), i = 1, 2, .. . , I, and t( j), j = 1, 2, . . . , J be
reference and test vector sequences, respectively. The
objective is to align the two sequences in time via a
nonlinear mapping (warping). Such a warping is an
ordered set of tuples as given below
(i
0
, j
0
), (i
1
, j
1
), . . . , (i
f
, j
f
),
where tuple (i, j) denotes mapping of r(i) to t( j), and
f + 1 is the number of mappings. The total cost D of
a mapping between r and t with respect to a distance
function d(i, j), is defined as the sum of all distances
between the mapped sequence elements
D =
f
∑
k=0
d(i
k
, j
k
), (1)
where d(i, j) measures the distance between elements
r(i) and t( j).
A mapping can also be viewed as a path on a two-
dimensional (2D) grid of size I × J, where grid node
(i, j) denotes a correspondence between r(i) and t( j).
Each path on the 2D grid is associated with a total cost
D given in (1). If the path is a complete path defined
by
(i
0
, j
0
) = (0, 0), (i
f
, j
f
) = (I,J), (2)
then a complete path aligns the entire sequences r and
t.
The minimum cost path on the 2D grid is the op-
timal alignment between two sequences. One way to
find the minimum cost path is to test every possible
path from the left-bottom corner to right-top corner.
However, this has exponential complexity. Dynamic
programming reduces the complexity by taking ad-
vantage of Bellman’s principle (Bellman, 1954). Bell-
man’s optimality principle states that the optimal path
from the starting grid node (i
0
, j
0
) to the ending node
(i
f
, j
f
) through an intermediate point (i, j) can be ex-
pressed as the concatenation of the optimal path from
(i
0
, j
0
) to (i, j), and the optimal path from (i, j) to
(i
f
, j
f
). This implies that if we are given the opti-
mal path from (i
0
, j
0
) to (i, j), we only need to search
for the optimal path from (i, j) to (i
f
, j
f
) rather than
searching for paths from (i
0
, j
0
) to (i
f
, j
f
).
Let’s use Bellman’s principle in total cost compu-
tation. If we denote the minimum total cost at node
(i
k
, j
k
) by D
min
(i
k
, j
k
), then by Bellman’s principle
D
min
(i
k
, j
k
) can be computed by using the costs of the
predecessor nodes, i.e. the set of i
k−1
, j
k−1
s, as below
D
min
(i
k
, j
k
) = min
i
k−1
, j
k−1
D
min
(i
k−1
, j
k−1
) + d(i
k
, j
k
),
(3)
where i
k−1
∈ {i
k
− 1, i
k
} and j
k−1
∈ { j
k
− 1, j
k
}.
GestureRecognitionusingSkeletonDatawithWeightedDynamicTimeWarping
621

Since all the elements are ordered in time, the set
of predecessor nodes are to the left and bottom of a
current node. An example set of predecessors which
includes only its immediate neighbors is given in Fig-
ure 1. Finally, the minimum cost path aligning two
sequences has cost D
min
(i
f
, j
f
), and the test sequence
is matched to the reference sequence that has the min-
imum cost among all reference sequences.
Although Equation (3) outputs the minimum cost
between two sequences, it does not output the optimal
path. To find the optimal path, which can be used to
map test sequence elements to reference sequence el-
ements, one needs to backtrack the optimal path start-
ing with the final node. If the the whole test sequence
is to be mapped to the whole reference sequence than
(i
f
, j
f
) = (I,J).
Using a weighting scheme in DTW cost computa-
tion has been proposed for gesture recognition (Reyes
et al., 2011). The method proposed in (Reyes et al.,
2011) uses DTW costs to compute between and
within class variations to find a weight for each body
joints. These weights are global weights in the sense
that there is only one weight computed for a body
joint. However, our proposed method computes a
weight for each body joint and for each gesture class.
This boosts the discriminative power of DTW costs
since a joint that is active in one gesture class may
not be active in another gesture class. Hence weights
has to be adjusted accordingly. This helps especially
dealing with within-class variation. To avoid reduc-
ing the between-class variance, we compute weights
by optimizing a discriminant ratio using a paramet-
ric model that depends on body joint activity. In the
next section we discuss data acquisition and feature
pre-processing.
3 DATA ACQUISITION AND
FEATURE PREPROCESSING
We use Microsoft Kinect sensor (Shotton et al., 2011)
to obtain joint positions. Kinect SDK tracks 3D coor-
dinates of 20 body joints given in Figure 2 in real time
(30 frames per second). Since the machine learning
algorithm uses depth images to predict joint positions,
the skeleton model is quite robust to color, texture,
and background.
We have observed that only six out of the 20 joints
contribute in identifying a hand gesture: left hand,
right hand, left wrist, right wrist, left elbow, right el-
bow. A feature vector consists of 3D coordinates of
these six joints and is of dimension of 18 as given be-
low
f
n
= [X
1
,Y
1
, Z
1
, X
2
,Y
2
, Z
2
, . . . X
6
,Y
6
, Z
6
], (4)
Hand Right
Wrist Right
Hand Left
Wrist Left
Elbow Left
Elbow Right
Head
Shoulder Right
Foot Right
Shoulder Left
Foot Left
Ankle Left
Ankle Right
Knee Left
Knee Right
Hip Left
Hip Right
Hip Center
Spine
Shoulder Center
Figure 2: Kinect joints.
where n is the index of the skeleton frame at time t
n
. A
gesture sequence is the concatenation of N such fea-
ture vectors.
After N feature vectors are concatenated to cre-
ate the gesture sequence, they are preprocessed before
the DTW cost computation. This preprocessing stage
eliminates variations in the feature vectors due to a
person’s size or its position in the camera’s field of
view. First, all feature vectors are normalized with the
distance between the left and the right shoulders to ac-
count for the variations due to a person’s size. A sec-
ond normalization follows by subtracting the shoul-
der center from all elements in f
n
, which accounts for
cases where the user is not in the center of the depth
image.
4 WEIGHTED DTW
The conventional DTW computes the dissimilarity
between two time sequences by aligning the two se-
quences based on a sample based distance. If the
sequence samples are multi-dimensional (18 dimen-
sional for the gesture recognition problem), using an
Euclidean distance gives equal importance to all di-
mensions. We propose to use a weighted distance in
the cost computation based on how relevant a body
joint is to a specific gesture class. The relevancy is
defined as the contribution of a joint to the motion
pattern of that gesture class. To infer a joint’s con-
tribution to a gesture class we compute its total dis-
placement during the performance of that gesture by
a trained user:
D
g
j
=
N
∑
n=2
Dist
j
(f
g
n
, f
g
n−1
), (5)
where g is the gesture index, j is the joint index and
n is the skeleton frame number. Dist
j
() computes the
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
622

displacement of joint j using two consecutive feature
vectors f
g
n
, and f
g
n−1
of gesture g.
After the total displacements are calculated, we
filter out the noise (e.g, shaking, trembling) and
threshold them from the bottom and the top. This pre-
vents our parametric weight model to output too high
or low weights as given below
D
g
j
=
D
a
if 0 ≤ D
g
j
< T
1
D
g
j
−T
1
T
2
−T
1
(D
b
− D
a
) + D
a
if T
1
≤ D
g
j
< T
2
D
b
otherwise,
(6)
where D
a
and D
b
are threshold values.
Using the total displacement values of joints, the
weights of class g are calculated via
w
g
j
=
1 − e
−βD
g
j
∑
k
1 − e
−βD
g
k
, (7)
where w
g
j
is joint j’s weight value for gesture class g.
Note that in this formulation a joint’s weight value can
change depending on the gesture class. For example,
for the right-hand-push-up gesture, one would expect
the right hand, right elbow and right wrist joints to
have large weights, but to have smaller weights for
the left-hand-push-up gesture.
To incorporate these weights into the cost, the dis-
tance function d(i
k
, j
k
) in Eq. (3) is defined to be
d
g
(i
k
, j
k
) =
∑
h
Dist
h
(f
g
i
k
, f
j
k
)w
g
h
, (8)
which gives the distance between the k
th
aligned pair,
(r(i
k
), t( j
k
)), where r is a sequence known to be in
gesture class g and t is an unknown test sequence.
The weights are obtained from the model given
in (7), which has a single parameter β. Our objec-
tive is to choose a β value that minimizes the within-
class variation while between-class variation is max-
imized. Between-class variation maximization and
within-class variation minimization can be achieved
by making irrelevant joints contribute less to the cost
(e.g., reducing the weights of right hand in left-hand-
push-up gesture) and not reducing (or possibly in-
creasing) the weights of joints that can help to dis-
criminate different gestures. We try to achieve this
goal by maximizing a discriminant ratio similar to
Fisher’s Discriminant Ratio (Kim et al., 2005).
First, we define D
mn
(β), as the average weighted
DTW cost between all samples of gesture class m and
gesture class n using weights calculated with given β.
Then between-class dissimilarity is the average of all
D
mn
(β)’s:
D
B
(β) =
∑
m
∑
n
n6=m
D
mn
(β). (9)
Within-class dissimilarity is the average DTW cost of
all sample sequences of class g with respect to each
other. The discriminant ratio (R) is obtained by
R(β) =
D
B
D
W
, (10)
where β is the model parameter to find the weights
used in DTW cost computation. The optimum β, β
∗
,
is chosen as the one that maximizes R:
β
∗
= arg max
β
R(β). (11)
5 RESULTS
We tested the performance of our proposed method on
our gesture database and compared it against the con-
ventional DTW method and a weighted DTW method
proposed by (Reyes et al., 2011). The database we
have created using Microsoft Kinect consists of eight
gesture classes with 28 samples per gesture class.
Eight samples of each gesture class are performed by
trained users, while the remaining 20 samples are per-
formed by untrained users. These eight samples are
used in learning the total distance measures of each
joint in each class, which is required by our weight
model in (7). The 20 samples are more noisy in
terms of gesture-start, gesture-end, and joint move-
ments during the gesture performance. Two sample
gestures are shown in Figure 3. The gesture database
used in the experiments, source code for visualization
of gestures, source code used to produce the results
in this paper and more results are publicly available
1
.
The physical factors (e.g., distance from the Kinect
sensor to the user, illumination in the room) are kept
constant during the recording. Bad records due to
a bad gesture performance or Kinect’s human-pose
recognition failure, were manually deleted by using
an OpenGL based gesture visualizer. Each gesture
sample includes 20 joint positions per frame, and the
time difference between two consecutive frames. The
gesture database is available online and we are hop-
ing that it can be used for testing gesture recognition
algorithms.
We have tested the three algorithms, namely, con-
ventional DTW, weighted DTW by (Reyes et al.,
2011), and our proposed method on our gesture
database. The confusion matrices for the three algo-
rithms are given in Table 1, 2, and 3. After creat-
ing the confusion matrices, we computed the overall
recognition accuracies according to the following for-
mula:
A = 100 ·
Trace(C)
∑
m
i=1
∑
n
j=1
C(i, j)
, (12)
1
http://mll.sehir.edu.tr/visapp2013
GestureRecognitionusingSkeletonDatawithWeightedDynamicTimeWarping
623

Figure 3: Two sample gestures: Right Hand Push Up and Left Hand Wave.
where A denotes the accuracy, and C denotes the con-
fusion matrix.
Our proposed method outperforms the weighted
DTW method in (Reyes et al., 2011) by a large margin
as given in Table 4. The reason is that their weights
are global weights, i.e., a joint’s weight is indepen-
dent of the gesture class. However, in our proposed
method a joint can have a different weight depend-
ing on the gesture class we are trying to align with.
This degree of freedom in computing the associated
DTW cost increases the reliability of DTW cost sig-
nificantly.
Table 1: Confusion matrix for unweighted DTW.
R push up
L push up
R pull down
L pull down
R swipe L
L swipe R
R push up 65 0 0 30 5 0
L push up 15 40 0 0 45 0
R pull down 0 0 85 15 0 0
L pull down 15 0 0 75 10 0
R swipe L 0 0 0 30 70 0
L swipe R 15 0 0 5 55 25
6 CONCLUSIONS
We have developed a weighted DTW method to boost
the discrimination capability of DTW cost, and shown
that the performance increases significantly. The
weights are based on a parametric model that depends
on the level of a joint’s contribution to a gesture class.
The model parameter is optimized by maximizing a
discriminant ratio, which helps to minimize within-
Table 2: Confusion matrix for state-of-the-art weighted
DTW.
R push up
L push up
R pull down
L pull down
R swipe L
L swipe R
R push up 65 0 0 30 5 0
L push up 15 45 0 0 40 0
R pull down 0 0 85 15 0 0
L pull down 15 0 0 80 5 0
R swipe L 0 0 0 30 70 0
L swipe R 15 0 0 0 55 30
Table 3: Confusion matrix for our weighted DTW.
R push up
L push up
R pull down
L pull down
R swipe L
L swipe R
R push up 100 0 0 0 0 0
L push up 0 100 0 0 0 0
R pull down 0 0 100 0 0 0
L pull down 0 0 0 85 15 0
R swipe L 0 0 0 0 100 0
L swipe R 0 0 0 0 5 95
Table 4: Accuracies of methods.
Method Accuracy
Classical DTW 60 %
State-of-the art 62.5 %
Proposed method 96.7 %
class variation and maximize between-class variation.
As a future work, we will be using Linear Discrimi-
nant Analysis (LDA) to compute weights, but the fact
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
624

that feature vectors may vary in length depending on
the gesture class is a difficulty that we will have to
deal with.
REFERENCES
Adams, N. H., Bartsch, M. A., Shifrin, J., and Wakefield,
G. H. (2004). Time series alignment for music infor-
mation retrieval. In ISMIR.
Amin, T. B. and Mahmood, I. (2008). Speech Recognition
using Dynamic Time Warping. In International Con-
ference on Advances in Space Technologies.
Baum, L. (1972). An inequality and associated maximiza-
tion technique in statistical estimation for probabilistic
functions of Markov processes. Inequalities, 3:1–8.
Baum, L. E., Petrie, T., Soules, G., and Weiss, N. (1970). A
Maximization Technique Occurring in the Statistical
Analysis of Probabilistic Functions of Markov Chains.
The Annals of Mathematical Statistics, 41:164–171.
Bellman, R. (1954). The theory of dynamic programming.
Bull. Amer. Math. Soc, 60(6):503–515.
D. Gehrig, H. Kuehne, A. W. and Schultz, T. (2009). Hmm-
based human motion recognition with optical flow
data. In IEEE International Conference on Humanoid
Robots (Humanoids 2009), Paris, France.
Kim, S.-J., Magnani, A., and Boyd, S. P. (2005). Robust
Fisher Discriminant Analysis. In Neural Information
Processing Systems.
Liang, R. and Ouhyoung, M. (1998). A real-time continu-
ous gesture recognition system for sign language. In
Automatic Face and Gesture Recognition, 1998. Pro-
ceedings. Third IEEE International Conference on,
pages 558–567. IEEE.
Myers, C. S. (1980). A Comparative Study of Several Dy-
namic Time Warping Algorithms for Speech Recog-
nition.
Rath, T. and Manmatha, R. (2003). Word image matching
using dynamic time warping. In Computer Vision and
Pattern Recognition, 2003. Proceedings. 2003 IEEE
Computer Society Conference on, volume 2, pages II–
521 – II–527 vol.2.
Rekha, J., Bhattacharya, J., and Majumder, S. (2011).
Shape, texture and local movement hand gesture fea-
tures for indian sign language recognition. In Trendz
in Information Sciences and Computing (TISC), 2011
3rd International Conference on, pages 30 –35.
Reyes, M., Dominguez, G., and Escalera, S. (2011). Feature
weighting in dynamic time warping for gesture recog-
nition in depth data. In Computer Vision Workshops
(ICCV Workshops), 2011 IEEE International Confer-
ence on, pages 1182 –1188.
Shotton, J., Fitzgibbon, A., Cook, M., Sharp, T., Finocchio,
M., Moore, R., Kipman, A., and Blake, A. (2011).
Real-time human pose recognition in parts from single
depth images. In CVPR, volume 2, page 7.
Starner, T. and Pentland, A. (1996). Real-Time American
Sign Language Recognition from Video Using Hid-
den Markov Models. In International Symposium on
Computer Vision.
Wenjun, T., Chengdong, W., Shuying, Z., and Li, J. (2010).
Dynamic hand gesture recognition using motion tra-
jectories and key frames. In Advanced Computer Con-
trol (ICACC), 2010 2nd International Conference on,
volume 3, pages 163 –167.
Wikipedia (2012). Dynamic Time Warping.
http://en.wikipedia.org/wiki/Dynamic time warping.
[Online;accessed 01-August-2008].
Wilson, A. D. and Bobick, A. F. (1999). Parametric Hid-
den Markov Models for Gesture Recognition. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 21:884–900.
GestureRecognitionusingSkeletonDatawithWeightedDynamicTimeWarping
625
