Predicting Evacuation Capacity for Public Buildings
Pejman Kamkarian
1
and Henry Hexmoor
2
1
Electrical and Computer Engineering Department, Southern Illinois University, Carbondale, IL 62901, U.S.A.
2
Computer Science Department, Southern Illinois University, Carbondale, IL 62901, U.S.A.
Keywords: Networks of Bayesian Belief Revision, Public Space Safety, Crowd Evacuation.
Abstract: This paper demonstrates a solution for analyzing public space evacuation rates. Evacuating from a public
building in a reasonable amount of time is reliant upon how safe the space is in terms of achieving a
minimum time to move people outside. In order to increase the safety of evacuation in public spaces, we
employed the Bayesian Belief Network method. To have a better estimation pattern, we have to focus on
important physical environmental features as well as crowd formation and specifications in a public space.
1 INTRODUCTION
Locations and geometric information are essential
attributes for the study of public space safety that
guide superior interior layout and designs for indoor
spaces. At the intersection of architectural concerns
and crowd specifications, assuring safety is a
ubiquitous concernin regards to how crowds react to
arising situations which can be caused by some other
symptoms related to life threatening triggers such as
fire, earth quake, burglary, terrorist attacks, and
bomb threats. In linguistic terms, the term ‘crowd’ is
a mass noun. Although it shares some properties
with other mass nouns such as air and water, it has
some behavioural differences from them.
Crowds often use spaces and pathways in
unintended ways. This usage stems from collective
group behaviors that emerge from an individual’s
propensity to spend the least amount of effort to
vacate the premises. Resulting effects are
unpredictable. Although, in some cases, such as
attempting to exit through exit doors, minimizing
distances to an exit is not a guiding principle,
whereas minimizing travel time to an exit is more
likely.
Crowd density is important as the number of
people in a unit of indoor space which is not
homogenous. Our primary objective is to develop a
device to be able to predict the safety of a public
space. We wish to use Bayesian Belief Networks to
provide building designers with a capability to
simulate and experiment in order to have a safer
environment. We intend that our model will be a
useful tool that supplements guidelines for future
building design codes.
Although no design improvement can prevent
disasters, careful designs can mitigate and
significantly reduce frequency of occurrence. Our
approach is multipronged. We explore the nature of
crowds as well as the structural properties of
buildings and then suggest a methodology for the
designing and managing of indoor environments. In
order to produce a better estimate of a public space
safety, we must investigate the behavior of the
crowd during various situations. We also need to
consider salient features of the crowd, such as the
average age and health status, which can affect
crowd dynamic movement and hence should be
considered.
We need a model that explains how and why
crowds may encounter emergencies. We also need to
build a model that explains disparate types of crowd
behaviors that are possible in various public places,
such as stadiums and transportation stations (Still,
2000). Virtual egress analysis and simulation System
are fundamentally an intractable problems. By a
process of behavioral rule, elimination behaviors are
reduced to four interactive rules pertaining to
objective, utility, constraint, and assimilation. These
four attributed rules produce crowd behavior that is
regular in contrast to the chaos of ordinary life. We
outline a few interactions between a crowd and its
environment. We also outline the development,
validation, and early results of a technique for
determining the character and critical dynamics
relating to a collapsing building. Our aim is not to
433
Kamkarian P. and Hexmoor H..
Predicting Evacuation Capacity for Public Buildings.
DOI: 10.5220/0004217704330440
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 433-440
ISBN: 978-989-8565-39-6
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

reproduce a model which is able to precisely make
decisions for a certain situation, or a specific public
space. Instead we strive to produce graphical
representations of patterns to demonstrate the
general reasons that may cause dangerous situations
in a prototypical public space.
The speed, density, and space utilization maps
allow us to qualitatively and quantitatively analyze
the use of space over time. This in turn facilitates a
greater understanding of the nature of the dynamics
of the crowd with respect to space requirements.
Some physical specifications of indoor public
spaces, such as the exit door width or locations of
installed ground facilities, should be considered.
For example, the exit door width could then be
increased to make crossing easier without flocking,
which can produce congestion that exceeds the
ultimate yield point for the area. Consideration
should also be given to the potential usage of
interconnected gates, also called concourses, by
spectators at events, such as public transportation
arenas. Usage can be considerable if the event spans
multiple hours, if inclement weather conditions are
present, or if a large population is attending.
Development of our pattern spans beyond our
current project. The crowd consists of many
individuals. Each simulated person computes his
least effort at every step in order to accomplish his
goals and other objectives of interest. Our aim is to
maximize utility in the context of applicable
constraints. Each entity has the capacity to react
according to its internal attributesas well as the
changes in the environment as the simulation
proceeds. The dynamics of the crowd are an
emergent phenomenon that is not programmed
explicitly.
In case of a group of people at an indoor public
space, as one of their natural actions, they may move
randomly in any allowed available public space.
Having no specific pattern of moving individuals
sometimes leads to having a large group of people in
the same space. This can be dangerous especially if
the position that the mentioned group of people
occupies is vulnerableor is sensitive to
overweighting. In such cases, lacking a suitable
strategy to make people aware about moving to any
other safe positions in the space leads to a disaster,
especially in public space such as inside a tower or
any upper levels of a building.
In this paper we demonstrate the Bayesian Belief
Networks as a significant solution to predict the
random movements of people through the indoor
space and predict the probability of gathering a large
group of them at any vulnerable points. The
Bayesian Belief Network performs this task by
having general specifications of the environment as
well as the people present in it.
Probabilistic reasoning and Bayesian Belief
Networks are widely used to predict behaviours in
many computational systems, such as in (Trautman
and Krause, 2010) that produced robotic navigation
routes amongst crowds using the least
probabilistically obstructed regions in dense
crowds.This is solving a classic robotic slow
decision making problem. Probabilistic evacuation
of a crowd escaping fire is simulated in (Pires, 2005)
where human cognitive processes are modelled. A
good survey of common crowd modelling and
simulation techniques is found in (Shendarkarb et.
al., 2008). In section 2 we will address a few guiding
principles. Section 3 outlines main tenets of
constructing a Bayesian Belief Network for the
purpose of predicting building safety. Sections 5 and
6 respectively describe a general methodology and a
specific example. Our paper culminates with Section
7 offering concluding remarks.
2 AN OVERVIEW OF PHYSICAL
ENVIRONMENTS AND
CROWD PROPERTIES
In order to predict a special pattern of gathering for a
group of people in a givenindoor location,
possessing a general knowledge of the public space
is essential. Some public spaces have more capacity
for allowing people to move and gather than others.
In order to have a good estimation ofplacing a large
group of people at a particular location, considering
various capacities is essential. We must consider the
position and placement of obstacles that are
normally fixed in the environment because they can
affect the crowd distribution patterns. We must also
know other facilities that are installed inside the
environment for people to use, such as vending
machines or performance stages. We need to
consider the geographic location of the building and
also the type of buildings or floors around the indoor
structure. We will briefly discuss modelling each
environmental key feature separately in
ourupcoming section on constructing a Bayesian
Belief Network.
2.1 Crowd Properties
Shortcut exploitation is a fundamental human
characteristic that we rely on as one of our guiding
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
434

principles. Another relevant human characteristic is
competitive nature, which will become important in
egress and ingress considerations. For instance, in
an evacuation, individuals will compete with one
another in progressing towards exits exploiting
optimal available paths. Our pattern will be a
predictive device for discovering the reasons that
may be caused by human characteristics in terms of
the collapsing of public spaces. Although guiding
principles dictate salient properties and behaviours,
they can hinder proper conclusions. Our pattern is
used to propagate microscopic human behaviours to
discover emergent properties. It will replace the
current macroscopic analyses that do not scale up
well.
3 BAYESIAN BELIEF
NETWORKS
Humanshavethe ability to recognizing relations
between different general attributes such as
geographic locations, cultural, and racial values and
norms (Davies and Russell, 1987). Generally there
are two kinds of relations: near-deterministic and
probabilistic. The relations between attributes, such
as the place of birth and racial origin, are classified
as near-deterministic because an Asian person who
is born in an Asian country is very likely to have the
same racial makeup as his/her Asian parent. All
other relations that are not crucially deterministic are
classified as probabilistic. For example, a person
who lives in Australia and is of Caucasian descent
will likely speakEnglish.
Bayesian Belief Network concentrates on
dependencies among existing attributes in a very
effective way. Instead of considering all possible
dependencies among attributes, it focuses only on
significant dependencies among all attributes
available in a domain. Generally, that provides a
compact representation of joint probability that is
distributed among all available attributes
consequently. While designing belief networks,
considering the most succinct and complex possible
graph representation is essential. In terms of a
graphical representation of belief networks that
consists of inter-connected networks,this is known to
be a NP-hard problem (Cooper, 1987).
Bayesian Belief Networks are investigated and
developed by many researchers (Pearl, 1986). It was
later called by many different terms such as
thecausal networks (Good, 1961-62), probabilistic
causal networks (Cooper, 1984), probabilistic
influence diagrams (Howard and Matheson, 1984);
(Shachter, 1986), and probabilistic cause-effect
models (Rousseau, 1968). At the early usage of this
application, it was applied to medical diagnostics.
For example, in terms of a technical aid supporting
medical experts, it was applied to a database which
consisted of many different symptoms and related
diseases in order to predict the kind of disease based
on a brief description of the observed symptoms
(Barnett et. al., 1998). This method became more
dominant henceforth. Microsoft has announced its
competitive advantages as including its expertise in
Bayesian Belief Networks (Helm, 1996). As future
examples of using Bayesian networks we can point
to robotic help and guidance (Berler and Shimony,
1997), software reliability assessment (Neil et. al.,
1996), data compression (Frey, 1998), and fraud
detection (Ezawa and Schuermann, 1995). One
broad usage of Bayesian Belief Networks is
applying it to product design. We use products
because of their functions and properties. They are
subject of artefacts (Roozenburg and Eekels, 1995).
Using Bayesian Belief Networks for customizing
products leads to build a product based on the
customer’s need. For example, producing a same car
would be varied if customers asked to have a fast car
in terms of speed or having a car in order to be able
to carry heavy and large objects.
A Bayesian Belief Network is a graphical
representation of probabilistic relationships between
a set of discrete attributes of the considerable
research. It consists of a directed acyclic graph such
that each node specifies a variable and the arcs
between nodes represent the independent relations
between variables. In such a graph, each variable is
conditionally independent of any combination of its
parent nodes (Frey, 1998). Each node has its own
conditional probability table which consists of all
possible states based on all possible states of its
parent nodes. For those nodes without any parent,
we will use an unconditional probabilities table.
In artificial intelligence, there are several
application classes that represent the probabilistic
relationships between different attributes using a
directed graph (Duda et. al., 1976); (Weiss et. al.,
1978). As a solution to represent uncertain
knowledge, Bayesian Belief Networks became
acceptable and popular among artificial intelligence
communities in the late 1980’s (Lauritzen and
Spiegelhalter, 1988); (Pearl, 1988). Later, the
Bayesian Belief Networks were applied in varies of
sciences, such as expert systems of diagnostic
systems.
PredictingEvacuationCapacityforPublicBuildings
435

4 CONSTRUCTION OF A
BAYESIAN BELIEF NETWORK
In order to demonstrate our Bayesian Belief
Network, we considered two separate work areas:
(a) indoor public space specifications, including both
indoor and some outdoor, and (b) the features of
people who are present in the space. We then
applied both indoor public space and the people
features on a unit of Bayesian Belief Networks
pattern.
4.1 Implementation
Generally, we have divided the employed attributes
of a building safety crowd evacuation into two
categories including (a) physical public space
specifications, and (b) Crowd specifications.
4.1.1 Physical Properties
Exploring physical specifications of building safety,
while investigating crowd safety evacuation is
essential. Most of the time, people are located in a
closed, covered area when they are gathered for a
certain event. They are sharing a common activity,
which is often related to the reason fortheir
gathering as a crowd. The following six features are
deemed detrimental.
Terrestrial sustainability: We considered natural or
other sources that can cause vibration for the indoor
space as an important factor. There are two general
sources that can affect a public space to be vibrating.
In terms of determining the safety of the building,
considering such sources are essential. The first
group of sources are natural and related to the area’s
geometric specifications that a public space is built
upon, such as the distance from any faults or
volcanoes. The second group of vibration sources
are created by human activity, such as a metro or
train facility. In addition to these, considering the
average weather status of the area is another key
feature that can affect the rate of vibration for the
structure. A public space that is located in a severe
weather area that has stormy weather frequently and
is prone to more vibrations than a structure that is
located in an area with a calm weather.
Flow capacity: We divided this feature into two
categories, the evacuation safety rate for (a)
examined indoor public space, and (b) for the
general building that the examined public space is
located inside. For indoor public space, we focused
on obstacles in terms of the number, installation
positions and also the average size of them. Each
public space has a number of emergency exit doors
as well as normal entrances that should be taken into
account. To have an estimate of safety for a general
building’s evacuation rate, we considered on all
existence obstacles that are located somewhere
between the indoor space and the main entrances of
the building. The numbers of such objects, as well as
the installation positions and the average size of
them, were the factors that we considered for this
category. As another key feature, we investigated the
type of the building such as a flat, an apartment, a
tower and so on. In case of being inside an
apartment or a tower, considering the level that
public space is located leads to having a better
estimation for the evacuation safety rate.
Overall exit capacity: Each door, based on its
location and width, has a different capacity to allow
passing a number of people through it at any
moment. We considered this feature for not only the
examined public space, but for all entrances that are
located between the interior space and the outside.
First Aid recovery capacity: In emergency cases,
proper extinguisher tools that are installed on
reasonable locations can help people stay alive and
safe for a longer time before being they can evacuate
from dangerous situations. For example, in case of
fire, using existing fire extinguishers near the fore
source will help people stay alive inside the area for
a longer time before evacuation.
Structural integrity: To have a better building safety
estimate, considering the materials that public space
is made of as well as the age of the structure are
essential, especially in case of using old materials
that may expose people inside at higher risk than a
new building with new and superior material would.
Space occupancy rate:This factor can be determined
by the type of using the public space as well as the
shape and the variety of installed facilities inside. A
theatre or a conference room witha variety of rows
of chairs may house more people at any moment
than a storage room or an area consisting of a sort of
different offices.
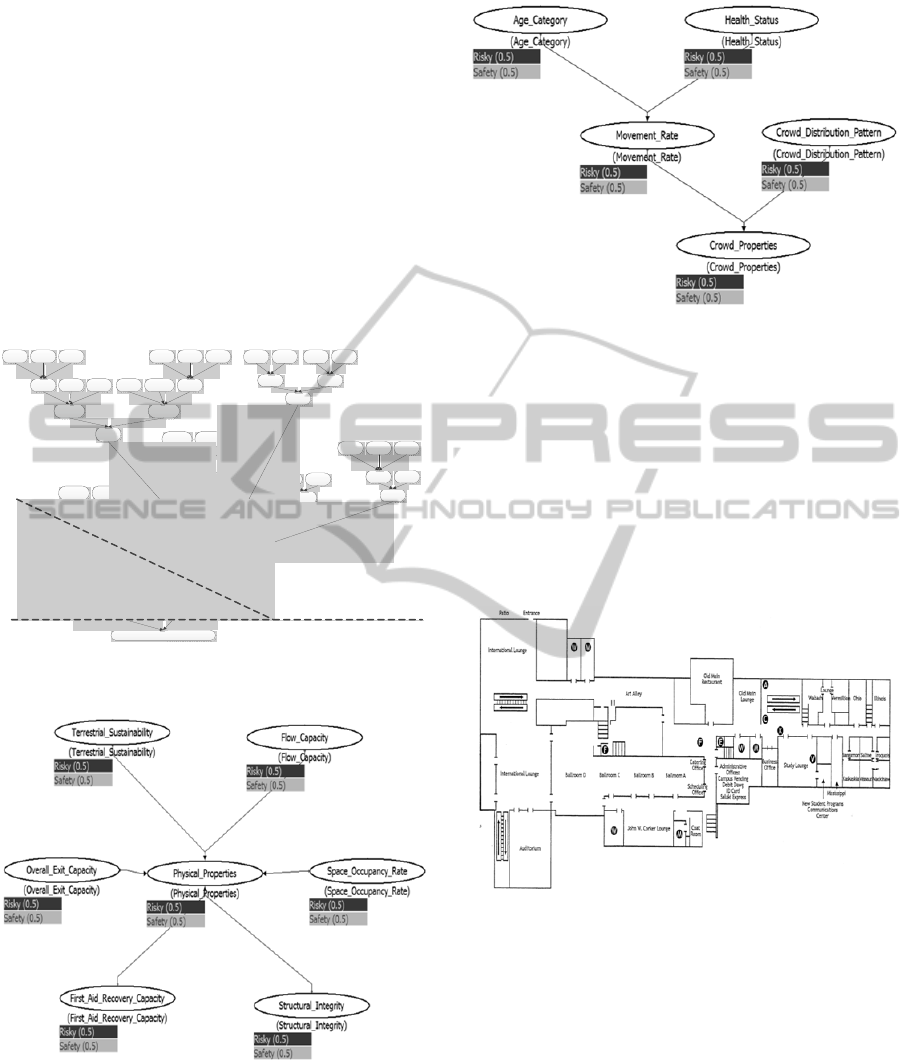
4.1.2 Crowd Properties
Considering movement rate, which is related to the
average age of the crowd as well as their average
health status, and the crowd’s normal distribution at
each moment leads us to a better estimation of the
crowd’s evacuation safety rate. As we hypothesize,
in a kindergarten class, the average age of the
majority of occupants will be below 10 years,
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
436

whereas in a conference room, it will be above 10.
In a hospital, as another instance, the average health
status is weak, whereas in a sports complex, health
can be assumed to be good.
5 NETWORK TOPOLOGY
We focused and classified all factors that are key
features for building our Bayesian Belief Network
structure. The proposed pattern may be varied while
considering different areas with different situations.
The Figure 1 represents the overall topology of our
general BBN network.
TerrainInstability
SourcesDistance
Manmade
Instability
Sources
Weat her
Instability
Sources
Terrestrial
Sustainability
Number of Exit
Doors
AverageWidt h
ofEx itDoors
Number of 
Interior Doors
AverageWidt h
ofInterior
Doors
ExitDoors
FlowSafety
Rate
Norm alFlow
SafetyRate
FlowCapaci ty
TotalNumber
ofExitDoors
TotalNumberof 
Norm alDoors
Buildi ngInt erior 
EvacuationRate
Materia lUsed StructureAge
Structural
Integrity
Crowd 
Occupancy
Arrang ment s
Obst ruct ion
FlowRate
Space
Occupancyrate
Typeof
Building
FloorLevel
(Ve rt i cal 
Distance)
Buildin gPe rim e ter 
EvacuationRate
Over al lExit
Capaci ty
Number of 
Install edSafety
Tools
Locati onof 
Install edSafety
Tools
FirstAid
Recovery
Capaci ty
ObstaclesObst acle s
PhysicalPropert ies
AgeCategory HealthStatus
Movement
Rate
Crowd
Distribution
Patter n
CrowdPrope rt ies
Publi cSafety
Numberof 
Obsta cle s
AverageSizeof
Obst acle s
Obsta cle 
Impasse Rate
Numberof 
Obsta cle s
AverageSizeof
Obstacles
Obstacle
Impasse Rate
Number of 
Obst acle s
AverageSizeof 
Obstacles
Obstacle
Impasse Rate
Figure2.BBNTop ology.Thedottedlinesrep res ent sub grou ps.
Figure 1: BBN topology.
Figure 2: Physical properties portion of BBN.
We constructed our model based on two general
sub graphs that are the children of the main BBN
root pattern. Figure 2 shows the physical properties
of the sub graphs, whereas Figure 3 shows the crowd
property’s sub graph.
Figure 3: Crowd properties BBN.
6 VALIDATIONS
We simulated a large ballroom public use space on
our campus. The building contains four floors and
our simulated ballroom is a frequently used space on
the second floor, housing international and
orientation events. Figure 4 depicts the floor plan of
the second floor, including our ballroom.
Figure 4: Layout of Ballroom D at the SIUC campus.
We explored the ballroom in order to assign it a
safety rating. During active events, the non-occupied
space between the ballroom and the outside doorway
is 40% of total space. The average size and
occupancy with obstacles is about 50% of the empty
space, which is distributed in a normal fashion for
the available space.
We constructed the conditional probability table
(CPT) for obstacles where we considered both
values for nodes B, and C, as safety and hence, the
obstacle node value becomes 0.9 or 90%, which is
classified as a safety situation.
PredictingEvacuationCapacityforPublicBuildings
437

Our student centre building has four floors, which
classifies it as a multilevel building. Because
ballroom D is located at the second floor, the value
of the Type of Building node is determined to be
risky. The floor level vertical distance is classified as
risky as well.
Regarding the CPT for building perimeter
evacuation capabilities, the building perimeter
evacuation rate is classified as a safety node, with a
50% chance of safety. In terms of considering indoor
space during events, about 50% of space is occupied
by different obstacles, installed with a normal
distribution, with the average size of 50%.
With regards to the CPT for obstacles, such node
indicates safety value. There are also two exit doors
as well as two normal entrance doors available
inside the space. We consider those values as two
nodes: total number of exit doors and total number
of normal doors, hence they indicate a safety value.
Regarding CPT for the building’s interior evacuation
rate, it has a safety value of 90%. Based on the total
number of exit doors and their width, as well as the
number of normal interior doors, referring CPTs for
exit doors’ flow safety rate and normal flow safety
rate, exit doors are classified as safe nodes. Hence,
regarding CPT for flow capacity, the IO safety rate
shows a safe value based on its parent nodes. This
node has a chance of 90% for safety. There are no
first aid recovery tools installed inside the public
area. The number of installed safety tools’ node, as
well as their location values on the CPT, will be set
as risky. As a result of parent nodes, the first aid
recovery capacity node becomes risky, which
indicates a risky situation for this part of the BBN
tree. In this case, this node has only a 10% chance of
safety. During data gathering for the installed
facilities, such as chairs, the available empty space is
less than 30% of the total area. Based on the number
of facilities installed inside the area, their position,
and their average size, the CPT for Crowd
Occupancy arrangements indicates a risky situation.
The average size and installed positions both will be
set to safe. This leads to CPT computations for the
obstruction flow rate node, which is a safe node with
70% chance of safety. This place is built for
gathering purposes with enough space inside. We
classified the crowd occupancy arrangements as a
safe node. Having the values of both nodes, the
obstruction flow rate node and the crowd occupancy
arrangement node, on the relative CPT for space
occupancy rate, leads us to have the space
occupancy rate as a safety value with a 90% chance
of safety. The following figure 5 shows the yearly
average climate status of the examined area.
Figure 5: The yearly average climate status of the
Carbondale.
Based on the area’s yearly average weather
status, this area is located in a windy/stormy position
for most days of the year, so we will classify the
Weather Instability Sources node as risky. The
distance from this area to the train rails is less than 3
kilometers. Hence, we considered a risky value for
the Manmade Instability Sources node. The
following figure 6 shows the geographic details of
the examined region.
Figure 6: Earth fault close to Carbondale (New Madrid).
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
438

Based on the map in Figure 6, the building is far
from major earth quake faults and mountains with
volcanoes. Therefore, we considered the value of the
Terrain Instability Sources as a safe node. Regarding
CPT for Terrestrial Sustainability, and based on the
values of parent nodes, Terrestrial Sustainability
value becomes safe with a 50% chance for safety.
The majority of the building is constructed with
concrete, which permits us to assign a safety node
for Material Used. It was built on 1925, so the
Structural Age will be set as risky. In regards to CPT
for Structural Integrity, the value of structural
integrity has a value of safe with a 50% chance of
safety. Usually, the majority of age for people within
the building is between 15 to 50 years of age. The
majority of health status is also healthy for the
people who gather inside this place. The values of
both age category and health status nodes are safe
values. For CPT of movement rate, the child node
movement rate becomes safe. It has a 90% chance of
safety. When forming a crowd, they usually have a
50% distribution over the whole area, which means a
normal distribution. The crowd distribution Pattern
node, hence, shows a safe value with a 90% chance
of safety. Regarding crowd properties, and based on
the parent nodes for the crowd properties node, it
presents a safety value and a 90% chance of safety.
Regarding to parent nodes values of the physical
properties node, it indicates a safety value, a 90%
chance for safety.
Figure 7: The CPT diagram for Physical Properties node.
Figure 7 shows risky factors to rate proportions.
Of all safety factors discussed in the previous
section, if only one indicated as an unsafe situation,
the unsafely rate for the whole system become 0.1.
In other terms, there is a 90% chance of safety. The
safety rate for the whole system decreases by
increasing the number of unsafe factors, as indicated
in Figure 7.
As determined by the final measurements,
regarding CPT, and based on the values of the parent
nodes, physical properties and crowd properties, the
value of the child node of the public safety node will
be determined. This node reflects a safety measure
and a 90% chance for safety.
7 CONCLUSIONS
This paper explored the Bayesian Belief Network as
a mechanism for evaluating potential risks that can
be generated due to unpredictable crowd movements
at any position of a building. Bayesian Belief
Network is able to predict the probability of
gathering a large group of people at a particular
position by focusing on general attributes of the
examined environment as well as the people who are
in it. Therefore, it is essential to have such a
mechanism in case of forming a large group of
people in the examined indoor public spaces,
especially when the space is located in upper levels
of the building. It helps security agents to consider
the vulnerability and strengths of a public space.
This can prevent the arising of any potential risk that
can occur because of emergencies, such as
overweighting. In order to evaluate efficacy of our
methodology, we are gathering data for a real world
set of buildings on our campus and early results are
promising.
REFERENCES
Barnett, G. O., Famiglietti, K. T., Kim, R. J., Hoffer, E. P.,
Feldman, M.J., 1998. DXplain on the Internet. In
American Medical Informatics Association 1998
Annual Symposium.
Berler, A., Shimony, S. E., 1997.Bayes Networks for
Sonar Sensor Fusion.In Geiger, D, Shenoy, P (eds)
1997.Proceedings of the Thirteenth Conference on
Uncertainty in Artificial Intelligence Morgan
Kaufmann.
Cooper, G. F., 1984. NESTOR: A computer-based
medical diagnostic aid that integrates causal and
probabilistic knowledge.In Ph.D. dissertation.Medical
Information Sciences, Stanford University.
Cooper, G. F., 1987. Probabiistic inference using belief
networks is NP-hard.In Technical Report KSL-87-27,
Medical Computer Science Group.Stanford
University.
Davies, T. R., Russell, S. J., 1987. A logical approach to
reasoning by analogy. In IJCAI 10. pp. 264–270.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
123456
Risky
Factors
PredictingEvacuationCapacityforPublicBuildings
439

Duda, R. O., Hart, P. E., Nilsson N. J., 1976.Subjective
Bayesian methods for rule-based inference systems.In
Proceedings of the 1976 National Computer
Conference (AFIPS Press). pp. 1075-1082.
Ezawa, K. J., Schuermann, T., 1995.Fraud/Uncollectible
Debt Detection Using a Bayesian Network Based
Learning System: A Rare Binary Outcome with Mixed
Data Structures. In Besnard, P, Hanks, S (eds)
Proceedings of the Eleventh Conference on
Uncertainty. in Artificial Intelligence Morgan
Kaufmann.
Frey, B. J., 1998.Graphical Models for Machine Learning
and Digital Communication.In MIT Press.
Good, I.J., 1961-62.A causal calculus (I & II).In British
Journal of the Philosophy of Science.pp. 305-318 12:
43-51.
Helm, L., October 28, 1996.Improbable Inspiration.In Los
Angeles Times.
Howard, R. A., Matheson, J. E., 1984. Influence
Diagrams. In Howard, R. A. and Matheson, J. E.
(eds.).The Principles and Applications of Decision
Analysis, (Strategic Decisions Group, Menlo Park,
CA). pp. 721-762.
Lauritzen, S. L., Spiegelhalter, D. J., 1988. Local
computations with probabilities on graphical structures
and their application to expert systems. In Journal of
the Royal Statistical Society.Vol.50 No. 2 pp.157-224.
Neil, M., Littlewood, B., Fenton, N., 1996.Applying
Bayesian Belief Networks to Systems Dependability
Assessment.In Proceedings of Safety Critical Systems
Club Symposium, Leeds.6-8 February 1996 Springer-
Verlag.
Pearl, J., 1986. Fusion, propagation and structuring in
belief networks. In Artificial Intelligence 29 241-288.
Pearl, J., 1988. Probabilistic Reasoning in Intelligent
Systems: networks of plausible inference.In Morgan
Kaufmann.
Pires, T. T., 2005. An approach for modeling human
cognitive behavior in evacuation models, In Fire
Safety Journal, Vol. 40, No. 2, March 2005, Pages
177–189, Elsevier Pub.
Roozenburg, N. F. M., Eekels, J., 1995. Product Design:
Fundamentals and Methods.In Wiley.
Rousseau, W. F., 1968. A method for computing
probabilities. In complex situations, Technical Report
6252-2. Stanford University Center for Systems
Research.
Shachter, R. D., 1986.Intelligence Probabilistic
inference.In Kanal, L. N., Lemmer, J. F. (eds.),
Uncertainly in Artificial Intelligence (North-Holland,
Amsterdam). pp. 371-382.
Shendarkarb, A., Vasudevana, K., Leea, S., Son, Y., 2008.
Crowd simulation for emergency response using BDI
agents based on immersive virtual reality, Simulation
Modelling Practice and Theory, Vol. 16, No. 9, Pages
1415–1429, Elsevier Pub.
Still, G. K., 2000. Crowd dynamics,
Doctoral dissertation.
University of Warwick, U. K.
Trautman, P., Krause, A., 2010. Unfreezing the Robot:
Navigation in Dense, Interacting Crowds, IROS
proceedings, pp. 797-803, IEEE press.
Weiss, S. M., Kulikowski C. A., Amarel S. and Safir
A.,1978. A model-based method for computer-aided
medical decision making. In Artificial Intelligence.pp.
145-172.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
440