Optimizing Theta Model for Monthly Data

Fotios Petropoulos

and Konstantinos Nikolopoulos

2,3

Lancaster Centre for Forecasting, Lancaster University, Lancaster, U.K.

BEM Bordeaux Management School, Talence Cedex, France

The Business School, Bangor University, Bangor, U.K.

Keywords: Forecasting Accuracy, Competitions, Theta Model, Seasonality, Time Series.

Abstract: Forecasting accuracy and performance of extrapolation techniques has always been of major importance for

both researchers and practitioners. Towards this direction, many forecasting competitions have conducted

over the years, in order to provide solid performance measurement frameworks for new methods. The Theta

model outperformed all other participants during the largest up-to-date competition (M3-competition). The

model’s performance is based to the a-priori decomposition of the original series into two separate lines,

which contain specific amount of information regarding the short-term and long-term behavior of the data.

The current research investigates possible modifications on the original Theta model, aiming to the

development of an optimized version of the model specifically for the monthly data. The proposed

adjustments refer to better estimation of the seasonal component, extension of the decomposition feature of

the original model and better optimization procedures for the smoothing parameter. The optimized model

was tested for its efficiency in a large data set containing more than 20,000 empirical series, displaying

improved performance ability when monthly data are considered.

1 INTRODUCTION

The exploration of extrapolation techniques for

improved performance accuracy is a subject of great

importance for forecasters and econometricians. The

benefits rising from accurate predictions reflect

directly to minimizing production, inventory and

distribution costs in any kind of industry and

organization. Towards this direction, many

international forecasting competitions have

conducted (for example Makridakis et al., 1982;

Crone et al., 2011), aiming to provide an evaluation

framework for well known and widely used

approaches, such as exponential smoothing methods,

versus new techniques and expert methods proposed

by academics or practitioners. An additional target

of forecasting competitions would be the

performance comparison of combinations derived

from simple methods in contrast to more

sophisticated approaches. Most competitions would

include numerous time series in different

frequencies (weekly, monthly, quarterly, yearly

data) while the accuracy and overall performance

evaluation was conducted with the use of a set of

performance metrics, so that the conclusions would

be as generic as possible.

The M3 forecasting competition (Makridakis &

Hibon, 2000) is regarded as the most successful

competition to date, with more than 20 participants

coming from both academia and software

companies. The quest was the submission of

accurate point forecasts for 3,003 time series from a

variety of economic fields. The results of M3

competition have referred to numerous scientific

publications, while its data have been used for many

empirical researches. The Theta model

(Assimakopoulos & Nikolopoulos, 2000) achieved

the best performance across all other approaches,

which in many cases was statistical significant when

compared with standard benchmarks, such as

Damped and Single Exponential Smoothing (5.1%

and 9.5% accuracy improvement respectively for the

monthly data). Moreover, this performance was

consistent for almost all frequencies, with Theta

model having the best overall performance for

quarterly and monthly data and the second best

performance for other data. Moreover, the Theta

model was within the top five methods when yearly

data were considered.

The main purpose of the current research is to



explore possible improvements of the Theta model

190

Petropoulos F. and Nikolopoulos K..

Optimizing Theta Model for Monthly Data.

DOI: 10.5220/0004220501900195

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 190-195

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

towards the development of an “optimized” version

aiming to even more accurate forecasts when

monthly data are considered. In order to do this, it is

essential to explore the core of the model, enumerate

its main attributes and investigate possible room for

improvements (Section 2). The next step would be

the setup of a series of experiments so that all

tunings and tweakings can be tested and the model

can be calibrated with the use of a limited data set of

monthly frequency series (Section 3). Finally, the

optimized model must be tested to a much larger,

extended data set so that to verify its validity

(Section 4). The last section of the paper (Section 5)

summarizes the conclusions and draws avenues for

future work.

2 EXPLORING THE THETA

MODEL

2.1 Original Theta Model

The original Theta model (Assimakopoulos and

Nikolopoulos, 2000) introduced a unique

decomposition of the original time series into two

separate lines, the so called “Theta Lines”. The

decomposition itself takes place to a seasonally

adjusted series and it is based on the modification of

the local curvature through a dedicated coefficient

(θ). Upon the selection of a unique θ coefficient, a

Theta line is calculated. All calculated Theta Lines

maintain the mean and the slope of the data,

regardless the value of θ. On the other hand, the

selected value of θ reflects directly to the local

curvatures of the series, with θ<1 resulting in series

where the primary qualitative characteristic would

be the improvement of approximation of the long-

term behavior of the data, whereas θ>1 creates series

with augmented short-term features. Originally, the

creators of the model decomposed the seasonally

adjusted series to just two Theta Lines with specific

θ coefficients (0 and 2). In more detail, Theta Line

(0) is nothing more than a linear regression line

(LRL) of the data, while Theta Line (2) represents a

line with double the curvatures of the original. Each

line is extrapolated separately, with Theta Line (0)

forecasts to be calculated as a usual extrapolation of

LRL, whereas Theta Line (2) is forecasted with

Single Exponential Smoothing (SES). The selection

of LRL and SES approaches is in line with the

characteristics of the two Theta Lines, in the sense

of their long-term and short-term features. Finally,

the forecasts of the two Theta Lines are combined

with equal weights and reseasonalized so that the

final point forecasts are derived.

So, in practice, the original approach of Theta

Model can be implemented by following the next six

steps:

Step 1: Seasonality Check. Original series is tested

for statistical significant seasonal behavior.

The criterion usually is the t-test value of

the autocorrelation function with lag one

year compared to value 1.645 (90%

significance).

Step 2: Deseasonalization. The time series is

deseasonalized via multiplicative classical

decomposition.

Step 3: Decomposition. Data are decomposed in

two Theta Lines, Theta Line (0) and Theta

Line (2).

Step 4: Extrapolation. Theta Line (0) is

extrapolated with LRL while Theta Line (2)

is extrapolated via SES.

Step 5: Combination. The forecasts produced from

the extrapolation of the two lines are

combined with equal weights.

Step 6: Reseasonalization. The combined point

forecasts are multiplicative reseasonalized.

2.2 Optimizations on Theta Model

Having analyzed the core of the original Theta

model, some modifications on the established

procedure may be proposed and tested for their

effectiveness. Firstly, there is serious empirical

evidence that forecasting accuracy can be improved

through better estimation of seasonal indices (Miller

and Williams, 2003), which lead to the calculation

of a more accurate seasonal adjusted series. The

current research investigates empirically the use of

three procedures for calculation of shrinkage

seasonal estimators. The first approach is an

adaption of the James-Stein shrinkage estimators

(James and Stein, 1961), which works effectively,

according to Miller and Williams (2003), under the

assumption that the estimated seasonal indices are

approximately symmetrical and single-peak, similar

in a sense to a normal distribution. The second

approach to be investigated is the Lemon-Krutchkoff

approach (Lemon and Krutchkoff, 1969), which is a

nonparametric empirical Bayes estimator with no

assumptions regarding the distribution of the

seasonal indices. Lastly, the third approach is a

selection framework developed by Miller and

Williams (2003), which recommends among

classical decomposition, James-Stein or Lemon-

Krutchkoff estimators based on both the value of

OptimizingThetaModelforMonthlyData

191

James-Stein shrinkage parameter and the

approximation of the seasonal indices distribution

(symmetric or skewed).

Another aspect to consider in the original Theta

approach would be the addition of more Theta Lines

during the Theta decomposition procedure. These

Theta Lines could effectively represented by any

value of θ coefficient, even negative ones. The

current research investigates the improvement on

accuracy when an additional Theta Line is

considered with an integer value in the range [-1, 3].

The value of the θ coefficient of the Theta Line to be

added should be defined after optimization and

testing through all possible values. Moreover, the

weights of the participated Theta Lines are to be

explored. The simple any generic solution of equal

weights should be questioned against the use of

optimized unequal weights. Both optimizations

would take place to a hidden-out subsample of the

data.

Lastly, attention should be paid on the

appropriate selection of the level smoothing

parameter (α) of SES method. Theoretically α

smoothing parameter should take any value in the

range [0, 1]. The optimized smoothing parameter is

to be selected after measuring which one results to

the best model fit. The measurement of the

appropriate α value generally takes place with Mean

Square Error (MSE). The current study explores

other accuracy metrics for this purpose, namely

Mean Percentage Error (MPE), Mean Absolute

Percentage Error (MAPE) and Symmetric Mean

Absolute Percentage Error (sMAPE). Furthermore,

empirical evidence has previously shown that

optimization should exclude marginal values (near 0

or near 1). As a result, we examine the impact of

excluding marginal values by selecting different

symmetric or asymmetric ranges. At last, a forced

minimization of the α value is considered, as a path

towards excluding the possibility for SES to act as

Naïve (which is the case for α=1) and a way to

“pressure” the model for even more smoothed point

forecasts.

3 CALIBRATING OPTIMIZED

THETA MODEL FOR

MONTHLY DATA

3.1 Empirical Data and Calibration

Procedure

The calibration procedure took place on the 1,428

monthly series of the M3 forecasting competition.

Data was coming from a variety of sources, such as

industry, macro, micro, finance, demographic and

other, while their median length was 115

observations. The forecasting procedure that was

followed was quite simple and straightforward. At

first, the last 18 observation of each series were

considered unknown and were hidden from the

sample, as to be in line with the procedure followed

by the organizers of the M3. Then, every potential

optimization discussed on subsection 2.2 was

applied independently for the calculation of

forecasts with horizon equal to 18 periods. The

accuracy of the modified models was measured and

compared to the original performance of the Theta

model. The accuracy metric used for this purpose

was the symmetric mean absolute percentage error,

which is defined in equation (1).











sMAPE

100

(%)



(1)

3.2 Optimizations on Estimation of

Seasonality

One basic aspect of the Theta model is the handling

of seasonality through steps 1, 2 and 6. So, an even

better estimation of the seasonal indices would result

in more accurate forecasts. As mentioned in

subsection 2.2, three shrinkage seasonal estimators

approaches where implemented and investigated

regarding their accuracy in contrast to the classical

decomposition method. The accuracy results of the

new estimations are presented in Table 1.

Table 1: Accurate estimation of seasonal indices.

Calculation Method for Seasonal Indices sMAPE (%)

Classical Decomposition Method 13.85

James and Stein 13.79

Lemon and Krutchkoff 13.83

Miller and Willians 13.78

It is clear that all three approaches result in more

accurate forecasts, due to the lower respective values

of the sMAPE. The best performance is observed for

the selection framework of Miller and Williams,

with gains up to 0.5% from the original model. This

conclusion is in line with the research of Miller and

Williams (2003).

3.3 Optimizations on Theta Lines

Two modifications were tested regarding

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

192

the decomposition lines of the Theta model. The first

one explores an automated selection, through error

minimization, of the weights by which the two

original Theta Lines (0 and 2) will contribute to the

final forecast. Several ranges for the weights to vary

were tested. The accuracy results were compared to

the original model, where both lines participated

with equal weights. The automated selection

procedure was achieved in each series independently

by holding-out of the fitting of the model an extra

subset of 12 observations. The second modification

on the original model investigates the possible

addition of an extra Theta Line with θ coefficient

taking values into the range [-1, 3]. The weight of

the contribution for the extra line is also to be

explored. Once again, the single series optimization

was conducted by building the model fits without

the last 12 available observations, which were used

for automatic model evaluation. The results for the

optimization upon Theta Lines are presented in

Tables 2 and 3.

Table 2: Unequal Theta Lines weights within specific

ranges.

Range for automatic weights sMAPE (%)

Equal Weights 13.85

[45%, 55%] 13.65

[40%, 60%] 13.70

[35%, 65%] 13.83

[30%, 70%] 14.00

Table 3: Adding one more line in the Theta model.

Function for final model sMAPE (%)

50% × L(0) + 50% × L(2) 13.85

33.3% × L(0) + 33.3% × L(2)

+ 33.3% × L(x)

14.34

45% × L(0) + 45% × L(2)

+ 10% × L(x)

13.71

47.5% × L(0) + 47.5% × L(2)

+ 5% × L(x)

13.70

50% × L(0) + 30% × L(2)

+ 20% × L(x)

13.74

50% × L(0) + 40% × L(2)

+ 10% × L(x)

13.68

In more detail, the effect on accuracy of unique

weight selection of Theta Lines for each series

within a specific range is presented in Table 2. Even

if almost all presented ranges result in better

accuracy in contrast to the original model, the best

performance is captured when a relatively small

range is selected. The performance improvement

against the original model is equal to 1.4%. The

accuracy results of the extra Theta Line are

presented in Table 3. A 10% weight on the extra

Theta Line is regarded as beneficial, especially in

the case that it is subtracted from the weight of

Theta Line(2). In this case, the accuracy among all

1,428 monthly series is as low as 13.68%, which can

be translated as an improvement equal to 1.3% from

the original model. As previously mentioned, the

value of θ coefficient may vary from series to series,

as well as this value is to be selected automatically

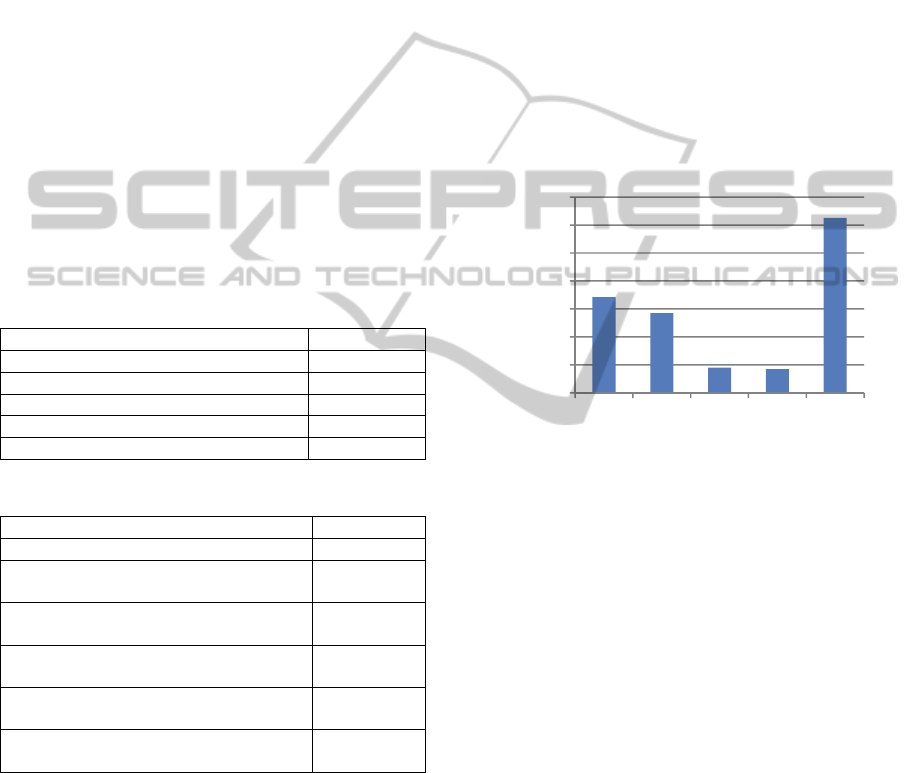
through out-of-sample optimization. Figure 1

demonstrates the distribution of the selected θ values

for all series. In most cases, value 3 is selected,

which represents a line with triple the curvatures of

the original data, followed by values -1 and 0. The

selection of the value -1 for almost 24% of the cases

is quiet unexpected, considering the nature of Theta

Line (-1), which represents a line with symmetric to

the LRL curvatures from the original.

Figure 1: Distribution of θ value across series.

3.4 Optimizations on SES

The last set of modifications was applied on the

selection of optimal smoothing parameter for the

level of the SES method. The accuracy results, when

constraint optimization ranges are applied, are

presented in Table 4. As the results indicate, there is

very small room for improvements, while the best

performance is recorded for the range [0.1, 0.9], as

expected. This approach leads to a small benefit

versus the original model, at just 0.2%. Table 5

demonstrates the effect of alternatives measure

metrics used during in-sample optimization of the α

smoothing parameter. The widely used MSE is

proved to be by far the best option. This is probably

due to the nature of the metric, which gives a higher

penalty on larger errors. As a result, there is

absolutely no need to do any adjustments here.

Lastly, the effects of by force decrement of the

selected smoothing parameter are explored in Table

6. It is easily interpretable that the value of sMAPE

100

200

300

400

500

600

700

-10123

Number of Time Series

θ-value

OptimizingThetaModelforMonthlyData

193

as a function of the percentage of forced decrement

for the smoothing parameter has a minimum at 30%,

equal to 13.803%. This improvement can be

translated as a partial optimization of 0.34% from

the original model.

Table 4: Range for selecting optimal smoothing parameter.

Range sMAPE (%)

[0, 1] 13.85

[0.1, 1] 13.84

[0.2, 1] 13.89

[0, 0.9] 13.84

[0, 0.8] 13.87

[0.1, 0.9] 13.82

Table 5: Measure metric for optimization.

Measure Metric sMAPE (%)

MSE 13.85

MPE 14.81

MAPE 15.77

sMAPE 14.91

Table 6: Forced decrement of selected smoothing

parameter.

% of by force

decrement

sMAPE (%)

0% 13.850

5% 13.824

10% 13.813

20% 13.804

30% 13.803

40% 13.838

50% 13.901

3.5 Overall Performance of the

Proposed Adjustments

Sections 3.2 to 3.4 demonstrated the potential

improvement on accuracy when only one at a time

modification was applied. By selecting the best case

of each possible adjustment, we proposed a

calibrated ‘optimized’ Theta model for monthly

series. The model’s overall accuracy performance,

when the test data are considered (M3 competition’s

monthly series), is presented in Table 7 and

contrasted by the accuracy of the five best

performers on M3 competition. The overall gain in

accuracy is measured just above 2% of the original

model. The importance of this improvement is more

obvious when compared to the performance of

Damped Exponential Smoothing Method (DES), a

method widely considered for benchmarking.

Original Theta model is just 5.1% better than DES,

whereas optimized Theta model is 6.9% better than

DES. Moreover, optimized Theta model is superior

to the average performance of all methods of the M3

competition (sMAPE=15.35%) by 13.33%, while

original Theta model does so by just 9.77%.

Table 7: Accuracy of the optimized Theta model.

Method sMAPE

(%)

M3 Rank

Original Theta model 13.85 1

Forecast Pro 13.86 2

Forecast X 14.45 3

Combination of SES-HES-

DES

14.48 4

Damped Exponential

Smoothing

14.59 5

Optimized Theta model 13.57 -

4 EVALUATION OF THE

OPTIMIZED MODEL

In order to verify the accuracy performance of the

optimized Theta model, a much larger set of time

series was collected. In fact, more than 20,000 series

were used for this evaluation procedure, coming

from empirical forecasting competitions, Federal

Reserve Bank of St. Liouis, Hyndman’s Time Series

Data Library as well as collections from textbooks.

Regarding the time frequency of the gathered data,

data sets included other than monthly, yearly,

quarterly, weekly and daily data. A hold-out set of

observations, corresponding to the frequency of the

time series, was kept unknown during the

calculation of the model fits and it was used only for

out-of-sample evaluation. Original Theta model and

optimized Theta model were compared also against

widely used forecasting techniques, namely SES,

Holt Exponential Smoothing (HES), DES and LRL.

The accuracy results are presented in Table 8, along

with the requested forecast horizon for each

frequency. The results indicate a clear advantage of

the optimized Theta model, as long as monthly data

are considered (about 3 out of 4 series). In general,

original Theta model is still the best option against

all examined methods, with the best overall

performance, followed by the proposed optimized

model.

5 CONCLUSIONS AND FUTURE

WORK

During the current research, various optimizations of

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

194

Table 8: Evaluation results of the optimized Theta model.

Yearly Quarterly Monthly Weekly Daily Other All

Forecast

Horizon

6 8 12 12 14 10 -

Method

SES 25.40 21.90 6.44 10.83 19.68 7.23 11.03

sMAPE (%)

HES 36.76 23.20 8.86 10.78 19.42 5.25 14.79

DES 28.76 14.11 6.78 11.40 20.63 6.52 11.02

LRL 39.21 74.97 12.56 43.42 36.32 11.19 23.45

Theta 22.20 13.93 6.30 10.87 19.76 5.91 9.64

Optimized

Theta

22.84 15.55 6.12 11.24 19.53 6.00 9.77

the top performer of the M3 International

Forecasting Competition (Makridakis and Hibon,

2000), the Theta model, were considered. The Theta

model can be described as a more generic

framework, in which the deseasonalized series are

decomposed in two or more Theta lines, each one of

which represents different amount of information.

The next stage constitutes of the extrapolation of the

decomposed lines via various forecasting

techniques. Then the forecasts are combined and the

final point forecasts are calculated. Originally, the

Theta model implementation was suggesting

decomposition into two symmetric Theta lines,

extrapolation with LRL and SES and simple

combination (equal weights). We investigated

further the dynamics of the Theta model, mostly

considering time series of monthly frequency, into

three specific directions:

1. Accurate estimation of seasonal indices

with the use of shrinkage methods against

the classical decomposition method.

2. Decomposition into up to three Theta lines

and alternative combination weights of the

decomposed forecasts into the final model.

3. Optimizations on the smoothing parameter

of the SES method.

The performance exploration of the proposed

modifications took place on the monthly series of

the M3 competition. The empirical results indicate

an overall performance gain of about 2% compared

to the original implementation. The proposed

model’s superiority on monthly data was verified on

a much larger data set containing more than 20,000

time series.

As far as future work is concerned, there are

many possible paths that could be investigated.

Firstly, a link between the weights of the Theta

forecasts into the final model with the forecasting

horizon should be investigated. Secondly, the

selection of the “appropriate” Theta lines should be

explored also as a matter of the qualitative and

quantitative characteristics of each series. Thirdly, a

framework for the selection of the most proper

extrapolation technique for each Theta line is to be

investigated. Finally, the theoretical underpinnings

of the optimized Theta model have to be examined.

REFERENCES

Assimakopoulos, V. Nikolopoulos, N., 2000. The theta

model: a decomposition approach to forecasting,

International Journal of Forecasting, Vol. 16, No. 4,

pp. 521-530.

Crone, S. F., Hibon, M., Nikolopoulos K., 2011. Advances

in forecasting with neural networks? Empirical

evidence from the NN3 competition on time series

prediction, International Journal of Forecasting, Vol.

27, No. 3, pp. 635-660.

James, W., Stein, C., 1961. Estimation with quadratic loss.

In Proceedings of the 4th Berkeley Symposium on

Mathematical Statistics and Probability, Vol. 1.

Berkeley, CA: University of California Press, pp. 361–

379.

Makridakis, S., Andersen, A., Carbone, R., Fildes, R.,

Hibon, M., Lewandowski, R., Newton, J., Parzen E.,

Winkler, R., 1982. The accuracy of extrapolation (time

series) methods: results of a forecasting

competition, Journal of Forecasting, Vol. 1, pp. 111–

153.

Makridakis, S., Hibon, M., 2000. The M3-Competition:

Results, conclusions and implications, International

Journal of Forecasting, Vol. 16, No. 4, pp. 451-476.

Miller, D., Williams, D., 2003. Shrinkage estimators of

time series seasonal factors and their effect on

forecasting accuracy. International Journal of

Forecasting, Vol. 19, No. 4, pp. 669-684.

Lemon, G. H., Krutchkoff, R. G., 1969. Smooth empirical

Bayes estimators: with results for the binomial and

normal situations. In Proceedings of the Symposium on

Empirical Bayes Estimation and Computing in

Statistics, Texas Tech University Mathematics Series

No.6, pp. 110–140.

OptimizingThetaModelforMonthlyData

195