
Alternative PPM Model for Quality Score Compression
Mete Akg
¨
un and Mahmut S¸amil Sa
˘
gıro
˘
glu
T
¨
ubitak B
˙
ILGEM, 41470, Gebze, Kocaeli, Turkey
Keywords:
FASTQ, Quality Scores, Prediction by Partial Matching (PPM), Compression.
Abstract:
Next Generation Sequencing (NGS) platforms generate header data and quality information for each nu-
cleotide sequence. These platforms may produce gigabyte-scale datasets. The storage of these datasets is
one of the major bottlenecks of NGS technology. Information produced by NGS are stored in FASTQ format.
In this paper, we propose an algorithm to compress quality score information stored in a FASTQ file. We try
to find a model that gives the lowest entropy on quality score data. We combine our powerful statistical model
with arithmetic coding to compress the quality score data the smallest. We compare its performance to text
compression utilities such as bzip2, gzip and ppmd and existing compression algorithms for quality scores.
We show that the performance of our compression algorithm is superior to that of both systems.
1 INTRODUCTION
Next generation sequencing platforms can generate
billions of short nucleotide sequences along with
quality scores and text data from the input DNA.
These data is stored in FASTQ file format. Some
algorithms and softwares such as sequence aligners
take these large volumes of data as input. The first
problem is the storage of these huge data. Nowadays,
computing clouds become more popular and useful.
Researchers that do not have enough computing re-
sources such as computer processors, memory, stor-
age, etc. use computing clouds. Another problem
is uploading these huge data to clouds via internet.
These problems make compression of FASTQ files
very important issue.
Sequence alignment and variation analysis are two
main applications in which FASTQ data are used by
researchers. In the literature, there are two type algo-
rithms for FASTQ compression: reference base and
no reference base. Reference base compression al-
gorithms try to compress all DNA reads by aligning
them to the reference genome. These algorithms are
suitable if there is a storage constraint. Feasibility of
the reference base compression is argued by the sci-
entific community. Some scientists say that it is not
feasible because sequence alignment takes too much
time. Others say that soft alignment algorithms that
only find exact matches can be used for the compres-
sion. No reference base compression algorithms use
some coding methods to compress raw FASTQ files.
These algorithms are used if there is no resource con-
straints in terms of storage and computation.
We mention two type of FASTQ compression
methods above. This classification is related with
compression of nucleotide sequences. In both meth-
ods, we also compress quality scores and text data.
Text data has very repeatable structure so it is very
efficient to compress it with already known methods.
The most important parts of FASTQ data are quality
scores for compression. Each quality score is repre-
sented with 6 bits so quality scores are the largest part
of FASTQ files. Some proposals provide lossy com-
pression for quality score compression. They claim
that low quality parts of sequencing data may be re-
moved because operations such as assembly or SNP
calling requires high quality parts of sequencing data.
Other proposals propound lossless solution for quality
score compression. Some of them claim that there is a
dependency between nucleotide sequence and quality
score sequence and consider the compression of qual-
ity score sequence together with nucleotide sequence.
In this paper, we consider the compression of
quality scores independently because there is no
statistical relation between nucleotide sequence and
quality score sequence. We examine the character-
istics of quality values in FASTQ files. We propose
a lossless compression algorithm to compress quality
score information stored in a FASTQ file. We try to
find a model that gives the lowest entropy on qual-
ity score data. We combine our powerful statistical
model with arithmetic coding to compress the quality
122
Akgün M. and ¸Samil Sa
˘
gıro
˘
glu M..
Alternative PPM Model for Quality Score Compression.
DOI: 10.5220/0004221601220126
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 122-126
ISBN: 978-989-8565-35-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

score data the smallest. We compare its performance
to text compression utilities such as bzip2, gzip and
ppmd and existing compression algorithms for qual-
ity scores. We show that our compression algorithm
outperforms these algorithms in terms of compression
rate and memory usage.
2 RELATED WORK
Wan et al. (Wan et al., 2012) focus on the com-
pression of quality scores. They investigate several
lossy and lossless transformations for quality scores.
They use each combination of these transformations
to compare several coding schemes. They point out
that simple coding schemes give better performance
to other methods.
Bhola et al. (Bhola et al., 2011) propose a sys-
tem to compress FASTQ files. Their system consid-
ers each component of a FASTQ file separately and
has unique compression method for each data field.
They use arithmetic adaptive coding (AAC) to encode
alpha-numeric and numeric fields in text data. Nu-
cleotide sequences are encoded by finding direct and
palindromic repeats for Markov encoding. They com-
pute entropy for six different representations of qual-
ity scores. The representation that yields the lowest
entropy is encoded with AAC.
Deorowicz and Grabowski (Deorowicz and
Grabowski, 2011) propose a compression algorithm
for FASTQ files. This algorithm use LZ77-style
encoding for nucleotide sequences and huffman
coding for quality scores.
Tembe et al. (Tembe et al., 2010) propose a com-
pression algorithm in which nucleotide and quality
scores are encoded together by using huffman coding.
Fritz et al. (Hsi-Yang Fritz et al., 2011) propose a
reference base compression algorithm for nucleotide
sequencing data. They propose a compression frame-
work for unmapped nucleotide sequences. They use
huffman based coding scheme for quality score com-
pression.
Wang et al. (Wang and Zhang, 2011) present
a reference based compression method (GRS) that
does not need any information about reference such as
SNPs map. Pinho et al. (Pinho et al., 2011) underline
that GRS is effective and takes less time when input
sequence and reference sequence have high similarity.
They also propose a statistical reference based com-
pression method. This method is based on probabilis-
tic copy model and takes two parameters to control
the performance of encoding for different sequences.
Kozanitis et al. (Kozanitis et al., 2010) propose
a lossless compression method for genomic sequence
fragments. They use Illumina Export format in their
study. They compare their method with bzip2. They
also propose a lossy method that uses a lossy qual-
ity value quantization. They claim that their lossy
method has minimal impact on SNP calls.
Reference base compression algorithms for high
throughput sequencing data are proposed in (Daily
et al., 2010) . The Relative Elias Gamma Indexed
(REG Indexed) encoding is primarily used for loca-
tion and mismatch information. In this study, the
compression of quality scores and identification in-
formation are not considered. In (Sakib et al., 2011),
an encoding scheme for sequence alignment data
in SAM (Sequence Alignment/Map) format is pre-
sented. There are some studies such as (Pinho et al.,
2008; Christley et al., 2009) that focus on compres-
sion of DNA data.
In Mar. 15 2012 James Bonfield (Bonfield, 2012)
won Pistoia Alliance compression contest for FASTQ
files. We can not find any tutorial or explanation
about this algorithm. All algorithms in the contest
were required to be published on Sourcefourge under
BSD-2 license. We got the source code of this algo-
rithm and explored its methods for quality score com-
pression. His implementation encapsulates a model
derived from Dmitry Shkarin and the range coder
from Eugene Shelwien. His algorithm compresses
quality scores by using low order range coder. The
range coder takes previous symbols, location of cur-
rent symbol in current row and the sum of difference
between current and previous symbol as inputs.
3 FASTQ FORMAT
Next generation sequencing platforms produce reads
consisting of a nucleotide sequence, probabilities that
the corresponding nucleotide is called incorrectly and
supporting information. These reads are stored in
text-based format called FASTQ. A FASTQ file nor-
mally uses four lines per sequence. Line 1 contains
sequence identifier beginning with a ’@’ character
and description. Line 2 contains nucleotide sequence
letters. Line 3 starts with ’+’ character and option-
ally contains sequence identifier and description. Line
4 contains quality values for nucleotide sequence in
Line 2.
In FASTQ format shown in Figure 1, error proba-
bility P is mapped into PHRED quality score Q. This
mapping is done by using some logarithmic equations
1,2.
Q
sanger
= −10 log
10
P (1)
Q
solexa
= −10 log
10
P
1 − P
(2)
AlternativePPMModelforQualityScoreCompression
123

@HWI-ST1030:93:C0BHGACXX:1:1101:1133:2327 1:N:0:
AAAATAGTTGTTATNGATATTCAAAT
+
BCCFFFFEHHHHHJ#2AFHJJJJJGI
@HWI-ST1030:93:C0BHGACXX:1:1101:1213:2333 1:N:0:
CAAATAATCTCTTTAATAACCTGATT
+
CC@FFFFFHHHHHJJGHHJJJIIEII
Figure 1: FASTQ Data.
4 PREDICTION BY PARTIAL
MATCHING - PPM
Prediction by Partial Matching (PPM) is a method that
makes statistical prediction about upcoming symbols
based on order n Markov Model (Cleary and Witten,
1984). It is a finite-context model because finite num-
ber of previous symbols are used for prediction. The
order of a PPM model is determined by the number of
previous symbols. Statistics gathered by PPM can be
used by entropy compression methods such as Huff-
man and Arithmetic compressions.
Data compression by PPM can be done with static
and adaptive models. The disadvantage of static vari-
ant is that statistics can consume more space than
compressed data. In adaptive variant, compression
starts with zero frequencies and this is the main prob-
lem of adaptive compression. If a model encounters a
novel symbol based on their context, it assigns escape
probability to the symbol. There are numerous studies
on PPM compression that try to improve compression
ratio by using some implementation tricks or different
data structures for context held by PPM model such as
(Cleary and Teahan, 1995; Cleary et al., 1995; Cam-
pos, 2000; Shkarin, 2002; Drinic et al., 2003).
5 A NEW MODEL FOR PPM
In this study, we focus on the compression of qual-
ity score data in FASTQ files. Firstly we observe
the compression rate of PPMD on quality score data.
PPMD is designed for general purpose. That means it
is a compressor for all text files. It is especially effec-
tive on natural language text. Therefore, the correct
way is to design a variant of PPM for quality score
data in FASTQ files.
PPM models are used to predict next symbols
from a varying number of previous characters. We
investigate the entropy of each quality score depend-
ing on previous scores. Furthermore, we calculate the
entropy of each quality score based on information
that how previous scores change. We keep this infor-
mation in binary format. For example, the previous
scores are CAAATA, we transform it to 110011. We
use 1 if the quality is not the same with the previ-
ous one or 0 otherwise. We implement these entropy
coders and compare their actual and expected com-
pression rates on our dataset. We observe that mod-
els with low entropy have lower compression perfor-
mance than expected values. This is because the pro-
portion of escape probabilities of models with higher
entropy is much higher than those of models with
lower entropy. Because of that there are too much
unused code space and these spaces can significantly
reduce execution speed. Based on our observation,
we use just one previous symbol to obtain best com-
pression results.
Our above observations lead us to use another in-
formation for encoding. Quality values in a row are
not related with quality values in another row. This
is because there is no physical relation between reads
produced by NGS. Furthermore, quality values for a
typical nucleotide sequence decrease towards the end
of the row. The characteristics of quality values in a
row make the location information of quality values
valuable for encoding.
We also observe that quality values for a read may
be higher, lower or moderate in some parts of a row.
Length of these parts are approximately twenty char-
acters. We use this observation in our model by taking
the average of previous twenty quality values.
In (Bonfield, 2012), James Bonfield use the dif-
ference between current and previous symbol in his
model. He takes the summation of these differences.
If the summation is not smaller than a threshold value,
it is used in his model otherwise threshold value is
used. It is very good way to represent character-
istics of quality values. His model can determine
whether quality values are getting worse or not. He
uses threshold value to represent this information with
fixed number of bits.
We encode quality scores using previous symbol,
location information of current symbol, the sum of
difference between current and previous symbol (δ)
and average of last twenty symbols before current
symbol (α). We use source code of fqz comp (Bon-
field, 2012) to implement our algorithm.
6 EXPERIMENTAL RESULTS
In this study, we design several entropy coders for
quality score compression. We use the combination of
previous symbols, variation of previous symbols and
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
124
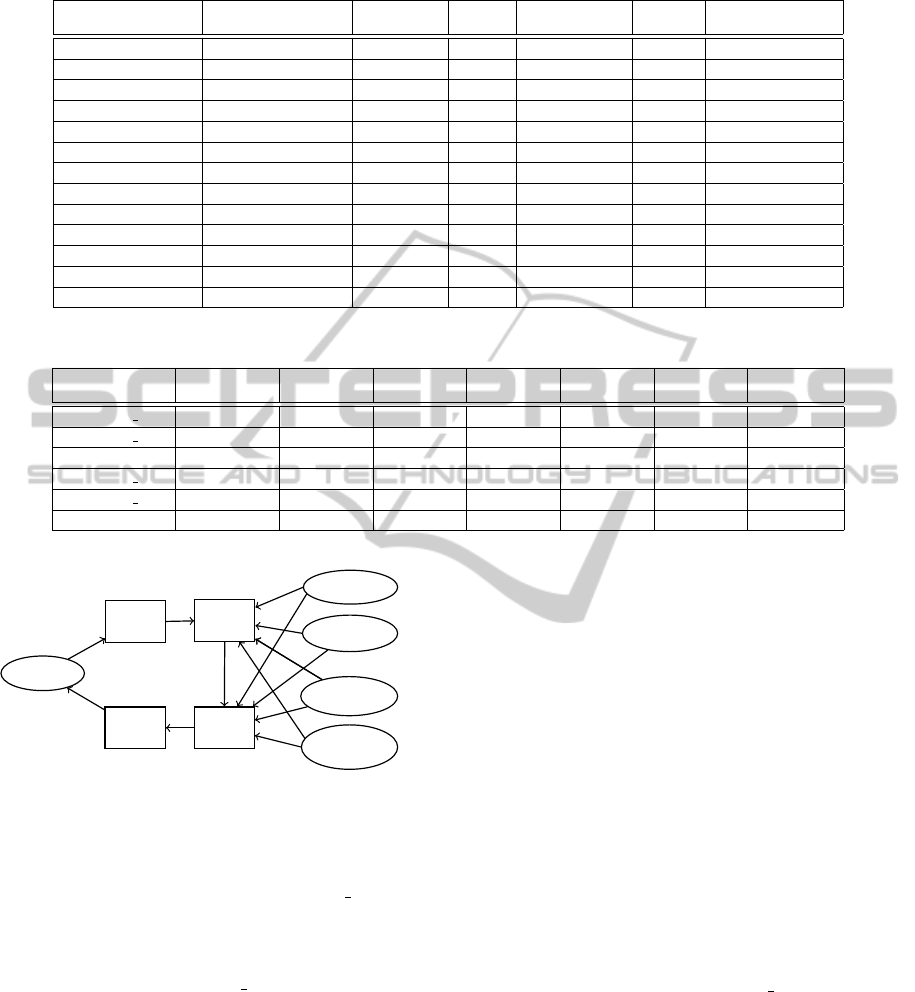
Table 1: Comparison of Entropy Coders.
Number of
Previous Symbols (a)
Variation of
Previous Symbols (b)
Location (c)
Information Format Number of Bits Entropy Compression Ratio
1 - - a 12 2.133 0.260
2 - - a 18 1.991 0.243
3 - - a 24 1.933 0.238
4 - - a 30 1.895 0.237
1 6 symbols - b+a 18 2.039 0.251
2 6 symbols - b+a 24 1.941 0.240
3 6 symbols - b+a 30 1.891 0.237
1 6 symbols 7 bits b+a+c 25 2.020 0.244
2 5 symbols 7 bits b+a+c 30 1.922 0.237
2 5 symbols 5 bits b+a+c 28 1,933 0.236
1 - 7 bits a+c 19 2.133 0.249
2 - 7 bits a+c 25 1.989 0.236
3 - 5 bits a+c 29 1.926 0.234
Table 2: Compression Results (File Size in Bytes).
FASTQ File
Size of
Scores gzip bzip2 ppmd
QScores
Archiver FqzComp
Our
Compressor
SRR007215 1.filt 118,607,138 75,970,863 71,804,695 70,334,701 79,452,712 64,401,957 65,740,172
SRR027520 1.filt 1,752,817,564 822,492,531 760,736,480 699,220,234 818,151,424 650,626,250 645,964,242
SRR032209 677,817,864 279,830,744 255,474,064 229,914,111 276,748,380 213,062,112 213,017,467
SRR062634 1.filt 2,414,899,300 809,651,027 695,959,063 615,874,056 764,523,316 563,661,233 562,261,738
SRR081224 1.filt 2,249,791,300 699,744,293 600,888,981 528,418,907 659,403,864 486,846,077 483,840,199
SRR089526 1,146,856,368 388,577,753 337,111,108 296,800,972 370,403,144 276,392,211 275,170,365
Entropy
Coding
Entropy
Decoding
Back
Scaling
Previous
Symbol
Location
Information
Sum of
Difference
Average of
last 20 symbols
Scaling
Quality Scores
Figure 2: Compression of Quality Scores with Entropy
Coding.
location of score for entropy computation. We design
arithmetic coder for each entropy. We test each en-
tropy coder on the FASTQ file SRR062634 1.filt. We
compare the performance of entropy coders in Table
1. In Table 1, compression ratio is defined as the ra-
tio of output file size and input file size. The size of
quality scores in SRR062634 1.filt is 2,439,048,293
bytes.
Our results show that entropy value and compres-
sion ratio decrease while the amount of information
increases. However, this brings burden of too much
memory. In our experiments, we use variation of
previous symbols. We keep this information in bi-
nary format. In this way, we can represent 6 previous
symbols in 6 bits. Our experiments show that previ-
ous symbols represented in 6 bits is much more valu-
able than 6 bits variation information. Furthermore,
that means while the distance between current sym-
bol and previous symbol increases, their dependency
decreases.
We use some other compression tools for compar-
ison. gzip and bzip2 are the two popular compres-
sors under Unix/Linux environment. PPMD (Moffat,
1990) is a variation of the PPM model. We also use
previously proposed algorithms for comparison Fqz-
Comp (Bonfield, 2012) and QScores Archiver (Wan
et al., 2012). We run FqzComp with parameter -q3
that gives the best result for fastq compression.
Our implementation is modified version of (Bon-
field, 2012). The configuration of our test machine
is Intel Core i7-2600 CPU 3.40 GHz 8, with 16 GB
internal memory.
Table 2 shows the results for different FASTQ
files. Our algorithm achieves the best compression
rate for all files except SRR007215 1.filt. For this
file FqzComp (Bonfield, 2012) achieves the best re-
sult. This file has read length of 26. It is too small
for gathering average information α. It shows that
our compressor may not give best results for FASTQ
files having small read length. Furthermore, memory
usage of our algorithm is the same with that of Fqz-
Comp algorithm (Bonfield, 2012). It requires approx-
imately 270 MB memory. QScores Archiver (Wan
et al., 2012) uses too much memory so we do not com-
pare the memory usage of this algorithm.
AlternativePPMModelforQualityScoreCompression
125

7 CONCLUSIONS
In this paper, we propose an algorithm to compress
quality score information stored in a FASTQ file. We
investigate the characteristics of a typical FASTQ file.
Based on our observations, We try to find a model
that gives the lowest entropy on quality score data.
We combine our powerful statistical model with arith-
metic coding to compress the quality score data as the
smallest. We compare its performance to text com-
pression utilities such as bzip2, gzip and ppmd and
existing compression algorithms for quality scores.
We show that our compression algorithm gives supe-
rior performance to that of these utilities and algo-
rithms.
Our study provides lossless compression method
for quality scores. Researchers claim that lossy com-
pression is suitable for quality scores because most
of the bioninformatics methods require nucleotide se-
quence with high quality scores. However their claim
is not always true for all conditions. For example,
lossy compression may cause wrong SNP detection
in low coverage parts of the genome.
While investigating FASTQ file for Illumina
Hiseq 2000, we observe that nucleotide sequences
that are produced from the same lane and swath have
similar quality score characteristics. This means reads
with locations close to each other have the same qual-
ity score structure. For future work, we will consider
this observation for quality score compression. Fur-
thermore, we will consider the compression of other
fields of FASTQ files. We will present a compression
system for FASTQ files.
REFERENCES
Bhola, V., Bopardikar, A., Narayanan, R., Leet, K., and
Ahm, T. (2011). No-reference compression of ge-
nomic data stored in fastq format. In Bioinformatics
and Biomedicine (BIBM), 2011 IEEE International
Conference on, pages 147 –150.
Bonfield, J. (2012). The fqzcomp com-
pression algorithm for fastq files.
http://sourceforge.net/p/fqzcomp/home/Home/.
Campos, A. (2000). Implementing ppmc with hash tables.
Christley, S., Lu, Y., Li, C., and Xie, X. (2009). Hu-
man genomes as email attachments. Bioinformatics,
25(2):274–275.
Cleary, J. and Teahan, W. (1995). Experiments on the zero
frequency problem. In Data Compression Conference,
1995. DCC ’95. Proceedings, page 480.
Cleary, J., Teahan, W., and Witten, I. (1995). Unbounded
length contexts for ppm. In Data Compression Con-
ference, 1995. DCC ’95. Proceedings, pages 52 –61.
Cleary, J. and Witten, I. (1984). Data compression using
adaptive coding and partial string matching. Commu-
nications, IEEE Transactions on, 32(4):396 – 402.
Daily, K., Rigor, P., Christley, S., Xie, X., and Baldi, P.
(2010). Data structures and compression algorithms
for high-throughput sequencing technologies. BMC
bioinformatics, 11(1):514+.
Deorowicz, S. and Grabowski, S. (2011). Compression of
dna sequence reads in fastq format. Bioinformatics,
27(6):860–862.
Drinic, M., Kirovski, D., and Potkonjak, M. (2003). Ppm
model cleaning. In Proceedings of the Conference on
Data Compression, DCC ’03, pages 163–, Washing-
ton, DC, USA. IEEE Computer Society.
Hsi-Yang Fritz, M., Leinonen, R., Cochrane, G., and Bir-
ney, E. (2011). Efficient storage of high throughput
sequencing data using reference-based compression.
Genome Research.
Kozanitis, C., Saunders, C., Kruglyak, S., Bafna, V., and
Varghese, G. (2010). Compressing genomic sequence
fragments using slimgene. In Proceedings of the 14th
Annual international conference on Research in Com-
putational Molecular Biology, RECOMB’10, pages
310–324, Berlin, Heidelberg. Springer-Verlag.
Moffat, A. (1990). Implementing the ppm data compres-
sion scheme. Communications, IEEE Transactions
on, 38(11):1917 –1921.
Pinho, A. J., Neves, J. R., and Ferreira, P. J. S. G. (2008).
Inverted-repeats-aware finite-context models for dna
coding. In Proceedings of the 16th European Confer-
ence on Signal Processing, EUSIPCO’08.
Pinho, A. J., Pratas, D., and Garcia, S. P. (2011). Green: a
tool for efficient compression of genome resequencing
data. Nucleic Acids Research.
Sakib, M. N., Tang, J., Zheng, W. J., and Huang, C.-T.
(2011). Improving transmission efficiency of large
sequence alignment/map (sam) files. PLoS ONE,
6(12):e28251.
Shkarin, D. (2002). Ppm: One step to practicality. In Pro-
ceedings of the Data Compression Conference, DCC
’02, pages 202–, Washington, DC, USA. IEEE Com-
puter Society.
Tembe, W., Lowey, J., and Suh, E. (2010). G-sqz: com-
pact encoding of genomic sequence and quality data.
Bioinformatics, 26(17):2192–2194.
Wan, R., Anh, V. N., and Asai, K. (2012). Transfor-
mations for the compression of fastq quality scores
of next-generation sequencing data. Bioinformatics,
28(5):628–635.
Wang, C. and Zhang, D. (2011). A novel compression tool
for efficient storage of genome resequencing data. Nu-
cleic Acids Research.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
126
