
Single Frequency Approximation of Volume Conductor Models
for Deep Brain Stimulation using Equivalent Circuits
Christian Schmidt and Ursula van Rienen
Institute of General Electrical Engineering, University of Rostock, Albert-Einstein-Str. 2, 18059 Rostock, Germany
Keywords:
Deep Brain Stimulation, Finite Element Method, Fourier Transform.
Abstract:
The objective of this study was to investigate the role of frequency-dependent material properties on the volt-
age response and neural activation in a volume conductor model for deep brain stimulation (DBS). A finite
element model of the brain was developed comprising tissue heterogeneity of gray matter, white matter, and
cerebrospinal fluid, which was derived from magnetic resonance images of the SRI24 multi-channel brain
atlas. A model of the Medtronic DBS 3387 lead surrounded by an encapsulation layer was positioned in the
subthalamic nucleus (STN). The frequency-dependent properties of brain tissue and their single-frequency
approximations were modelled as voltage- and current-controlled equivalent circuits. The frequency of best
approximation, for which the pulse deviation between the single-frequency and frequency-dependent voltage
response were minimal, was computed in a frequency range between 130 Hz and 1.3 MHz. Single-frequency
approximations of the DBS pulses and the resulting volume of tissue activated (VTA) were found to be in
good agreement with the pulses and VTAs obtained from the frequency-dependent solution. Single-frequency
approximations were computed by combining finite element method with equivalent circuits. This method
allows a fast computation of the time-dependent voltage response in the proximity of the stimulated target by
requiring only one finite element computation.
1 INTRODUCTION
Deep brain stimulation (DBS) is a neurosurgical
method to treat symptoms of motor disorders such as
Parkinson’s disease (PD), essential tremor and dys-
tonia and has emerged as an effective treatment (Uc
and Follet, 2007). Although the method has become
a common procedure in the clinical field of PD, the
fundamental mechanisms of DBS remain uncertain
(Montgomery Jr. and Gale, 2008). Computational
models can help to gain knowledge about these mech-
anisms by predicting field distributions and the neural
response in stimulated brain areas. The field distri-
bution which directly affects the neural response, and
therefore the stimulation benefit, is dependent on a
variety of factors. These factors concern, amongst
others, the model geometry (Walckiers et al., 2010),
the frequency-dependent electrical properties of brain
tissue (Grant and Lowery, 2010), the effects occurring
at the electrode-tissue interface (Cantrell et al., 2008)
and the reaction of the body to the electrode, result-
ing in the growth of a so-called encapsulation layer
around the electrode (Yousif and Liu, 2009).
The electric properties of biological tissue show a
frequency dependence over a wide spectrum (Gabriel
et al., 1996). To investigate the effect of dispersive tis-
sue in DBS an appropriate formulation of the under-
lying physics has to be made. Therefore, an electro-
quasistatic (EQS) formulation was used, which ap-
plies for the time-harmonic electric fields generated in
the proximity of the stimulated target by the applied
DBS pulse (van Rienen, 2000). In a preliminary study
it was concluded that dispersive effects of the electri-
cal tissue properties could be neglected under current-
controlled stimulation for appropriate conductivity
values (Bossetti et al., 2008). Results were obtained
by comparing a single frequency solution comprising
a fixed conductivity value with the dispersive solu-
tion in an homogeneous finite element model. These
results were expanded in a following study by using
an improved anatomically head model and compar-
ing dispersive solutions with single frequency solu-
tions under current- and voltage-controlled stimula-
tion (Grant and Lowery, 2010). However, the brain
tissue remained homogeneous and the deviation be-
tween the single frequency and dispersive solutions
of the model were investigated only at 100 Hz, 1 kHz,
and 1 MHz. In the mentioned study, the computation
38
Schmidt C. and van Rienen U..
Single Frequency Approximation of Volume Conductor Models for Deep Brain Stimulation using Equivalent Circuits.
DOI: 10.5220/0004223700380047
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 38-47
ISBN: 978-989-8565-36-5
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

of the voltage response at a position in the proximity
of the stimulated target was carried out using the so-
called Fourier finite element method, in which the re-
quired transfer function is determined by the electric
potential at this position for each frequency compo-
nent of the DBS pulse (Butson and McIntyre, 2005).
Since a precise modelling of a square-wave pulse with
a frequency of 130 Hz and a pulse width of 60 µs,
as used in DBS therapy, requires several thousand
Fourier components, the computation of the transfer
function even for an approximation at a single fre-
quency becomes rather computationally expensive.
We propose the use of equivalent circuits for the
approximation of the transfer function, in which the
electrical properties of the brain model are determined
by the resistance and capacitance of the volume con-
ductor model. The resistance and capacitance can be
computed for the single-frequency solution by only
one evaluation of the brain model, which allows a
time-efficient computation of the voltage response for
a single-frequency solution, and, therefore, facilitates
the comparison of the single-frequency solutions with
the frequency-dependent solution across a wide range
of frequencies. To date, the influence of the inter-
action of the different dispersive brain tissue types
on the approximation of the dispersive solution by
a solution in which the electrical properties are esti-
mated at a single frequency across a wide range of
frequencies remains unquantified. Therefore, the ob-
jective of this study was to investigate the influence of
frequency-dependent material properties of brain tis-
sue on the voltage response and neural activation for
200 different frequencies across a range from 130 Hz
to 1.3 MHz in an heterogeneous and anatomically
head model using an equivalent circuit approach.
2 METHODS
2.1 Finite Element Model
The geometry used for the brain consists of an ideal-
ized human brain modelled as an ellipsoid (Fig. 1).
The spatial dimensions of the brain model were de-
rived from the the SRI24 multi-channel brain atlas
which is a standard atlas of the human brain based
on magnetic resonance images (Rohlfing et al., 2008).
The atlas comprises averaged 3 T MRI images and
tissue segmentations with a voxel size of 1 mm
3
of
24 volunteers spanning from 19 to 84 years old. The
brain tissue is segmented into white matter, gray mat-
ter and cerebrospinal fluid. The position of the STN
was determined using a brain atlas and comparing
axial, coronal and sagittal slices of the T1-weighted
electrode
lead
region of
interest
unipolar ground
encapsulation
layer
4
3
2
1
110 mm
128 mm
19 mm
19 mm
coronary slice
region of interest
1.5 mm
1.27 mm
Figure 1: Coronary slice of the model geometry. T1 MRI
data of the SRI24 multi-channel brain atlas is shown in the
background.
MRI data with the atlas (Kretschmann and Weinrich,
1991).
A model of the Medtronic 3387 DBS electrode,
comprising 4 equidistantly spaced platin-iridium con-
tacts, was subtracted from the model preserving the
insulation and contact surface information for the ap-
plication of boundary conditions. The electrode lead
was implemented in the model with the second elec-
trode contact positioned in the centre of the stimu-
lated target. An encapsulation layer with a thickness
of 0.2 mm was incorporated around the electrode. To
apply unipolar electrode configurations, the bottom
of the ellipsoid was modelled as a plane circle with
a radius of 22 mm. The electrode tip and the stimu-
lated target was surrounded by a cube-shaped region
of interest (ROI) with an edge length of 19 mm, which
had a finer mesh density than the remaining brain
model. The segmented MRI dataset was preprocessed
in MATLAB to reformat the data to an right-handed
coordinate system, which was required by the finite
element software. A more detailed description of the
model geometry can be found in a preliminary study
(Schmidt and van Rienen, 2012).
2.2 Mesh Generation
The model was meshed with tetrahedral elements us-
ing the Delaunay method. The triangular mesh of the
electrode contact surfaces were manually refined un-
til the alteration of the integral of the current density
over the surface area of the active electrode was be-
low 1%, which was obtained for a maximum element
length of 0.1 mm. To avoid disconformity between
the tetrahedral mesh and the hexahedral elements of
the MRI data, the mesh within the ROI was set to a
maximum element length of 0.5 mm. The resulting
mesh of the brain model contained out of about 1.4
million elements.
SingleFrequencyApproximationofVolumeConductorModelsforDeepBrainStimulationusingEquivalentCircuits
39

2.3 Electrical Properties of Tissue
The conductivity and relative permittivity of biologi-
cal tissues, both, show a frequency dependence which
can be described by different dispersion regions each
expressed as a Cole-Cole term. The conductivity and
relative permittivity of gray matter, white matter, and
cerebrospinal fluid was computed by a 4 Cole-Cole
term expression using the data of an experimental
study (Gabriel et al., 1996). The electrical tissue prop-
erties of the encapsulation layer around the implant
vary over time from an acute phase immediately af-
ter surgery to a chronic phase after some weeks due
to cell growth in the layer. This results in an increase
of the resistivity compared to that of the brain tissue
(Grill and Mortimer, 1994). To model the longterm
effects of DBS, the encapsulation layer was modelled
in the chronic phase by using the halved conductivity
value of gray matter (Butson and McIntyre, 2005) and
the relative permittivity of brain tissue (Yousif and
Liu, 2009).
2.4 Finite Element Computation
The voltage distribution in the proximity of the stim-
ulated target as well as the resistance R and capaci-
tance C of the brain model was computed using finite
element method. Therefore, the electro-quasistatic
(EQS) formulation
∇[(σ(ω) + jωε
0
ε
r
(ω))∇φ] = 0 , (1)
with the electric potential φ, the imaginary unit j,
the angular frequency ω, the frequency-dependent
conductivity σ(ω), the frequency-dependent relative
permittivity ε
r
(ω) and the electric field constant
ε
0
≈ 8.854 · 10
−12
As/Vm, was applied to the brain
model, which is a valid approximation of the elec-
tromagnetic wave equation for bio-electrical applica-
tions in the human brain (Bossetti et al., 2008). The
exterior boundary of the idealized brain was modelled
as insulation using Neumann boundary condition. To
apply voltage-controlled or current-controlled stimu-
lation, the surface of the active electrode contact was
set to a constant potential or constant normal cur-
rent density, respectively. In both cases, the ground
electrode located at the bottom of the brain model
was set to a constant potential of φ
0
=0 V. The re-
maining electrode contacts were set to floating po-
tential, i.e. no net current flow occurring through
the contact surfaces. The finite element computa-
tions were performed with the commercial software
COMSOL Multiphysics. Quadratic shape functions
were used. The assembled linear system of equa-
tions was solved using generalized minimal residual
method (GMRES) with a geometric multigrid as pre-
conditioner. Iteration was stopped when the 2-norm
of the residual was below 1 ·10
−6
. The electric poten-
tial φ, the resistance R, and the capacitance C are de-
termined for 50 frequencies in each decade between
130 Hz and 1.3 MHz resulting in 200 frequencies.
The frequency-dependent resistance R(ω) and capac-
itance C(ω) were computed using the integral of the
current density over the surface area of the active elec-
trode contact with the expressions
R(ω) =
U
ℜ(I(ω))
, C(ω) =
ℑ(I(ω))
ωU
(2)
with the voltage U = φ
1
− φ
0
, and the real part ℜ(I)
and the imaginary part ℑ(I) of the current, while the
surface of the active electrode contact was set to a
constant potential of φ
1
= 1 V.
2.5 Waveform Computation
The DBS pulses applied to the DBS electrode in this
study are commonly used in DBS therapy and consist
of a monophasic square-wave signal with a pulse du-
ration of d
p
=60 µs, a frequency of f =130 Hz and a
cathodic amplitude of A
vc
=3 V for voltage-controlled
stimulation and A
cc
=1.5 mA for current-controlled
stimulation. The DBS pulses y(t) are modelled in
time-domain and transformed into frequency-domain
using a fast Fourier transform (FFT) with a sampling
rate of 1 MHz. Since an ideal square-wave signal has,
by definition, points of discontinuity, the Fourier syn-
thesis of the finite Fourier components X
k
of the signal
can result in an overshooting at these points, which
is in the order of 9 % for a square-wave signal, if the
Fourier synthesis is truncated. To avoid this effect, the
square-wave pulses were smoothed using the function
y(t) =
A
2
1 +tanh
a
d
p
2
− |t|
, (3)
with the slope coefficient a. The smoothing of the
signal reduces the influence of high frequency compo-
nents, and therefore the overshooting, but could also
influence the effect of tissue capacitance. To investi-
gate this effect, the DBS pulses were also modelled
as ideal square-wave signals by a step function using
the same pulse parameters. The slope coefficient was
set to 1 · 10
6
, which resulted in a cut-off frequency of
151 kHz (Fig. 2). At a cut-off frequency of 151 kHz
the square-wave signal is significantly smoothed, re-
ducing the overshoot below 0.1 %, while its overall
shape is preserved. To receive the voltage response
in the proximity of the stimulated target at a loca-
tion r, the Fourier components X
k
were scaled and
phase shifted by the transfer function T (ω) obtained
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
40

10 20 30 40 50 60 70 80 90 100
−3
−2
−1
0
time [µs]
voltage [V]
square−wave pulse
smoothed pulse
cut−off: 151 kHz
Figure 2: Voltage-controlled pulse modelled as a square-
wave signal (blue) and as a smoothed signal with a cut-off
frequency of 151kHz (green).
from the finite element computation by multiplying
the Fourier components X
k
component for component
with the transfer function T (ω
k
) at the correspond-
ing frequency ω
k
(Butson and McIntyre, 2005). In
the proposed method, this transfer function is approx-
imated using an equivalent circuit comprising the par-
allel RC circuit from the finite element model and
a constant phase element CPE, which models the
electrode-tissue-interface. The impedance Z
CPE
of
this interface is expressed by
Z
CPE
=
K
A
s
(jω)
β
(4)
where K = 1.51Ωm
2
s
−β
, β = 0.91, and the active
electrode contact surface area A
s
=5.98 µm
2
(Cantrell
et al., 2008). In vivo and in vitro measurements for
current controlled DBS stimulation showed a strongly
non-linear dependence of the double layer on the
stimulus amplitude for frequencies below 100 Hz, but
not at high frequencies above 100 Hz (Wei and Grill,
2009). For the used DBS pulses, the spectral energy
density below 130 Hz contains only about 1.5 % of the
total spectral energy density. Therefore, it is assumed
in this study, that the electrode-tissue-interface can be
modelled by the linear constant phase element.
2.5.1 Voltage-controlled Stimulation
The single frequency approximation of the transfer
function T
vc
for the voltage-controlled case was ob-
tained by using a constant potential boundary con-
dition on the surface of the active electrode con-
tact, resulting in a total voltage of A
vc,FEM
=1 V in
the finite element model. By using the equation for
a frequency-dependent voltage divider, the transfer
function T
vc
and the scaled Fourier components X
k,vc
at a position r are expressed by
T
vc
(ω
k
) =
1 +
1
R(ω
s
)
+ jω
k
C(ω
s
)
Z
CPE
(ω
k
)
−1
(5)
X
k,vc
(ω
s
) =
T
vc
(ω
k
)
|T
vc
(ω
s
)|
·
|φ(r,ω
s
)|
|A
vc,FEM
|
X
k
. (6)
Since the constant phase element is not incorporated
into the finite element computation, the frequency-
dependent transfer function for the voltage-controlled
case is obtained by multiplying the transfer function
T
vc
component for component with the frequency-
dependent voltage φ(r,ω) of the finite element com-
putation.
2.5.2 Current-controlled Stimulation
For current-controlled stimulation, the constant phase
element is negligible, since capacitive and disper-
sive effects dominate the waveform shape (Grant
and Lowery, 2010). Therefore, the transfer func-
tion T
cc
for the current-controlled case is only depen-
dent on the resistance R and capacitance C of the fi-
nite element model. For the computation of the volt-
age distribution φ(r, ω
s
), a normal current density
boundary condition was set on the surface of the ac-
tive electrode contact, resulting in a total current of
A
cc,FEM
=1.5 mA in the finite element model. The
resulting transfer function T
cc
and the scaled Fourier
components X
k,cc
at a position r are expressed by
T
cc
(ω
k
) =
1
R(ω
s
)
+ jω
k
C(ω
s
)
−1
(7)
X
k,cc
(ω
s
) =
T
cc
(ω
k
)
|T
cc
(ω
s
)|
·
|φ(r,ω
s
)|
|A
cc,FEM
|
X
k
. (8)
The transfer functions obtained from the finite el-
ement computations at the 200 frequencies in the fre-
quency range between 130 Hz and 1.3 MHz were lin-
early interpolated on the FFT frequency spectrum of
the DBS pulses. The voltage responses derived from
the single-frequency approximation using the equiva-
lent circuit models for voltage- and current-controlled
stimulation were compared with the voltage responses
derived from the frequency-dependent solutions at ra-
dial distances between 0.5 mm and 5 mm of the active
electrode contact.
2.6 Volume of Tissue Activated
The effect of the single frequency approximation of
the voltage response in the proximity of the electrode
contact on the neural activation was investigated using
SingleFrequencyApproximationofVolumeConductorModelsforDeepBrainStimulationusingEquivalentCircuits
41

a myelinated axon cable model described by McIn-
tyre et al. (McIntyre et al., 2002). The axon model
has a diameter of 5.7µm and includes 21 nodes of
Ranvier, paranodal and internodal segments as well
as the myelin sheath. At each node, the time depen-
dent voltage response was computed and used to de-
termine the threshold voltage V
t
using NEURON (7.2,
http://www.neuron.yale.edu). 100 axons were aligned
perpendicular to the coronary plane in a rectangular
10 × 10 grid with a spacing of 0.5 mm parallel and
perpendicular to the electrode axis. The grid was po-
sitioned caudal and centered to the active electrode
contact. The minimum stimulus amplitude necessary
to elicit action potential propagation in each axon was
determined using Brent’s method, as implemented in
the SciPy optimisation library (Jones et al., 2001).
For the stimulus of the applied pulses, the computed
threshold voltages in the grid were approximated by
a fourth order polynomial f (x) using least squares fit,
where x is the distance to the electrode centre. The
volume of tissue activated (VTA) was then computed
with disk integration using the roots of P(y) as the
interval boundaries.
3 RESULTS
The proposed method requires that the voltage
response at different locations can be computed by
using the same transfer function scaled by the voltage
at these locations. Therefore, the resulting voltage
responses at different locations should equal each
other except a scaling factor of their amplitude. To
investigate the validity of this requirement in the
proximity of the stimulated target, the normalized
voltage responses and transfer functions for a current-
controlled square-wave and smoothed stimulus in a
distance of 0.5 mm to 5 mm of the active electrode
contact were compared for a solution, in which the
values of the electrical properties of brain tissue were
determined at a frequency of 1 kHz. The deviation
between the root mean square (RMS) of the normal-
ized transfer function is below 0.4 % with respect to
the RMS at a distance of 5 mm (Fig. 3). The same
behaviour as for the deviation of the transfer function
can be observed for the normalized square-wave
voltage response at the different distances from the
active electrode contact. This deviation decreased
to below 0.04 % for the smoothed voltage response,
which is a result of the lesser spectral energy density
in the higher frequency components of the smoothed
DBS pulse compared to the square-wave DBS pulse.
Regarding the observed deviations of the transfer
function, and the square-wave as well as smoothed
1 2 3 4
0
0.1
0.2
0.3
0.4
distance [mm]
relative error [%]
transfer function
smoothed pulse
square−wave pulse
Figure 3: Relative error of the RMS of the normalized trans-
fer functions (red) as well as of the normalized square-wave
voltage responses (blue) and smoothed voltage responses
(green) for current-controlled stimulation with respect to
the values at a distance of 5 mm.
0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0.5
0.55
0.6
0.65
0.7
distance [mm]
relative error [%]
smoothed pulse
square−wave pulse
Figure 4: Relative error of the RMS of the single frequency
approximation using equivalent circuits for the normalized
square-wave voltage responses (blue) and smoothed voltage
responses (green) for current-controlled stimulation with re-
spect to the RMS of the voltage responses obtained from the
Fourier finite element method.
voltage response, the requirement of a transfer
function, which is independent of the location, is
considered to be fulfilled.
The square-wave and smoothed voltage response
for current-controlled stimulation obtained from the
Fourier finite element method were compared with
those obtained from the single-frequency approxi-
mation using equivalent circuits. The deviation of
the RMS of the square-wave voltage responses using
equivalent circuits remained between 0.52 % and
0.61 % compared to those obtained from the Fourier
finite element method, while a slight decrease of this
deviation is noticeable with increasing distance to
the active electrode contact (Fig. 4). The deviation
of the RMS of the smoothed voltage responses
remained between 0.51 % and 0.60 % and showed a
similar decrease with increasing distance to the active
electrode contact.
The single-frequency approximation of the
square-wave and smoothed voltage response for
voltage-controlled stimulation was compared with
their frequency-dependent solutions for 200 fre-
quencies in a frequency range between 130 Hz and
1.3 MHz at a distance of 1 mm to the active electrode
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
42
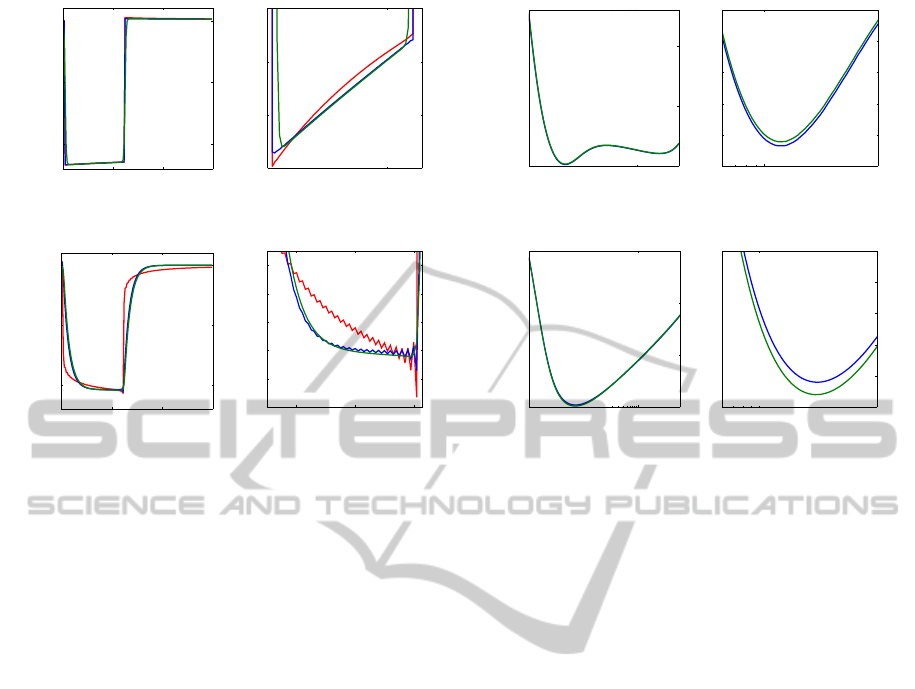
%
&
!"
#
$#
'
(
Figure 5: Left: Frequency-dependent voltage response of the square-wave DBS pulse (red) and single-frequency approxima-
tion of the square-wave (blue) as well as smoothed DBS pulse (green) at a frequency of 1.2 kHz. Right: Relative error of
the RMS of the single-frequency voltage responses with respect to the frequency-dependent voltage responses for the square-
wave (blue) and smoothed DBS pulse (green). (A-B) Voltage-controlled stimulation. (C-D) Current-controlled stimulation.
On the right of each sub image a magnified section is shown.
contact. The deviation between the single-frequency
pulses and the frequency-dependent pulses was
minimal at a frequency of approximately 1.2 kHz
(Fig. 5B). The relative error of the RMS of the
voltage responses at this frequency were 0.06 %
for the square-wave DBS pulse and 0.07 % for the
smoothed DBS pulse. Despite the smoothing of
the slope of the signal, no apparent difference exist
between the square-wave and smoothed voltage
response in the single-frequency approximation (Fig.
5A). The current-controlled pulse resulting out of the
frequency-dependent solution was best approximated
by the single frequency solution at a frequency of
approximately 2.2 kHz (Fig. 5D) with a relative
error of the RMS of 0.8 % for the square-wave DBS
pulse and 0.4 % for the smoothed DBS pulse. The
deviation of the single-frequency pulses and the
frequency-dependent pulses increased in the lower
and higher frequency range to 58 % and 36 % for
130 Hz and 1.3 MHz, respectively. These maximal
relative errors were much higher than compared to
those for voltage-controlled DBS pulses, which were
maximal 5.1 % at 130 Hz. The current-controlled
voltage responses for the square-wave DBS pulse
showed an overshooting of approximately 3 %, which
was noticeable for the smoothed DBS pulse (Fig.
5C). The overshooting in a discrete Fourier transform
results out of a truncation of high frequency com-
ponents of the Fourier spectrum of the DBS pulse
by the capacitive filtering of the electrical proper-
ties of brain tissue. This filtering is decreased for
voltage-controlled DBS pulses by the influence of the
constant phase element. Therefore, no overshooting
is noticeable for voltage-controlled DBS pulses (Fig.
5A).
The influence of the pulse duration of the DBS
pulses on the frequency of best approximation was
investigated for pulse durations between 60 µs and
120 µs, for which the suppression of symptoms
should occur (Medtronic, Inc, 2003). The frequency
of best approximation for the current-controlled DBS
pulse decreased monotonically from approximately
2.2 kHz to 1.4 kHz within the range of investigated
pulse durations, while that for the voltage-controlled
DBS pulse increased only slightly from approxi-
mately 1.2 kHz to 1.3 kHz (Fig. 6). The relative error
of the pulses approximated at a single-frequency
remained in each case below 0.8 %.
The volume of tissue activated (VTA) was
computed for a stimulus amplitude of 1 V for
voltage-controlled stimulation and 0.5 mA for
current-controlled stimulation (Fig. 7). The relative
error of the VTA computed for the single-frequency
square-wave DBS pulses at the best approxi-
mation frequency to the VTA computed for the
frequency-dependent DBS pulses was below 0.3 %
for voltage-controlled stimulation and 5.5 % for
current-controlled stimulation (Table 1). This relative
SingleFrequencyApproximationofVolumeConductorModelsforDeepBrainStimulationusingEquivalentCircuits
43

60 80 100 120
1.2
1.4
1.6
1.8
2
2.2
pulse duration [µs]
frequency [kHz]
60 80 100 120
0
0.2
0.4
0.6
0.8
pulse duration [µs]
relative error [%]
Figure 6: Frequency of best approximation and the corre-
sponding relative error of the RMS of the single-frequency
and frequency dependent voltage response for different
pulse durations of the DBS pulse. Voltage-controlled DBS
pulse (blue). Current-controlled DBS pulse (green).
0.5
1.25
2
Current-controlled [mA]
1
2.5
4
Voltage-controlled [V]
Figure 7: Computed thresholds for the activation of the ax-
ons for the frequency-dependent voltage responses scaled
by the stimulus amplitude of the current- and voltage-
controlled square-wave DBS pulses.
error was similar for the smoothed DBS pulses.
However, the VTA for the frequency-dependent DBS
pulses varied by 4.2 % for voltage-controlled stimu-
lation when smoothed DBS pulses were used instead
of square-wave DBS pulses. Since no overshooting
was noticeable in the voltage-controlled pulses, this
variation is presumably caused by the smaller slope
of the smoothed DBS pulse. For current-controlled
stimulation, this variation decreased to 1.5 %.
4 DISCUSSION
The deviation between the voltage response for
voltage- and current-controlled stimulation pulses as
well as for a smoothed version of the pulses was in-
vestigated in the proximity of the stimulated target.
The computation of this deviation was carried out at a
representative location in 1 mm distance to the active
electrode contact. This was possible, since the nor-
malized transfer function and the resulting voltage re-
sponses at different locations within the proximity of
the stimulated target were almost constant using the
Fourier finite element method (Fig. 3). Furthermore,
the voltage responses computed with the proposed fi-
nite element method in combination with equivalent
circuits were in good agreement with those computed
with the Fourier finite element method (Fig. 4). The
latter requires the computation of the transfer func-
tion with the finite element method for several har-
monics of the used DBS pulse, which vary between
513 (Yousif and Liu, 2009) and 2,000 (Grant and
Lowery, 2010) finite element computations for a com-
mon DBS pulse. Instead, the proposed method allows
a fast computation of the voltage-response in mod-
els with frequency-independent material properties by
only one evaluation of the finite element model plus a
minor computational effort in post-processing to com-
pute the transfer function.
The influence of the frequency-dependent electri-
cal properties of brain tissue on the voltage-response
was approximated by a finite element model using
frequency-independent values of the electrical prop-
erties of brain tissue by determining them at a sin-
gle frequency. The results indicate, that the voltage-
responses of the frequency-dependent model is in
good agreement with those of a single-frequency
model at approximately 1.2 kHz and 2.2 kHz for
voltage-controlled and current-controlled stimulation
(Fig. 5). These results are in agreement with a pre-
liminary study comparing single-frequency approxi-
mations of the voltage response with the frequency-
dependent solution for three different frequencies be-
tween 100 Hz and 10 kHz, suggesting that an estima-
tion of the material properties at a single frequency
may provide an approximation of the frequency-
dependent solution (Grant and Lowery, 2010). For
current-controlled stimulation, the overall devia-
tion between the single-frequency and frequency-
dependent voltage responses was larger than for
voltage-controlled stimulation in the observed fre-
quency band of 130 Hz to 1.3 MHz. This effect can be
ascribed to the constant phase element, which reduces
the influence of the frequency-dependent material
properties by scaling the representative impedance in
the transfer function. The frequency of best approx-
imation for current- and voltage-controlled stimula-
tion varied slightly between 1.3 kHz and 2.2 kHz for
different pulse durations of the DBS pulses (Fig. 6).
These frequencies are similar to the frequencies of the
first dispersive poles of the used electrical properties
in the proximity of the stimulated target, i.e. white
matter at 1.3 kHz and gray matter at 1.9 kHz (Gabriel
et al., 1996). The results suggest that the major in-
fluence of the frequency-dependent electrical proper-
ties of the used brain tissue can be found at frequen-
cies near those of the dispersive poles. Therefore, a
good guess of the frequencies for the single-frequency
approximation could be obtained by investigating the
frequency-dependent behaviour of the material prop-
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
44

Table 1: Computed volume of tissue activated (VTA) for the frequency-dependent and best approximated single-frequency
voltage responses for square-wave and smoothed DBS pulses as well as voltage-controlled and current-controlled stimulation.
DBS pulse Voltage-controlled VTA [mm
3
] Current-controlled VTA [mm
3
]
square-wave, frequency-dependent 60.53 46.48
square-wave, single-frequency 60.60 43.93
smoothed, frequency-dependent 57.96 45.76
smoothed, single-frequency 58.10 43.38
erties in the proximity of the stimulated target, which
can be achieved in pre-processing.
The computed VTAs for a stimulus amplitude
of 1 V for voltage-controlled stimulation and 0.5 mA
for current-controlled stimulation had an extent be-
tween 43.93 mm
3
and 60.60 mm
3
(Table 1). The
results of this study show a larger influence of the
frequency-dependent electrical properties of the tis-
sue for current-controlled stimulation. The voltage re-
sponse for voltage-controlled stimulation is basically
influenced by the capacitive effects of the electrical
double layer, while under current-controlled stimula-
tion the capacitive and dispersive effects of the bulk
tissue dominate the waveform shape. The latter ef-
fect results out of the explicit injection of the in-
ward current to the volume conductor model, lead-
ing to a negligible influence of the electrical double
layer capacitance on the waveform shape. There-
fore, higher deviations of the voltage response and
the VTA for current-controlled stimulation were ob-
servable, which are in agreement with the results in
literature (Butson and McIntyre, 2005). While the
extent for current-controlled stimulation was slightly
smaller than for voltage controlled stimulation, a
similar spatial pattern of the required thresholds for
the activation was noticeable (Fig. 7). Compared
to the deviations in the voltage response of the
single-frequency approximations to the frequency-
dependent solutions, the corresponding deviation of
the VTAs increased to 0.3 % for voltage-controlled
stimulation and 5.5 % for current-controlled stimula-
tion. This small deviations of the VTA are in agree-
ment with a computational study, in which the thresh-
olds for a single frequency approximation were com-
pared with the frequency-dependent solution for a
point source (Bossetti et al., 2008). While the ex-
tent of the VTA slightly increased for the single-
frequency approximation for voltage-controlled stim-
ulation, it decreased in current-controlled stimulation,
which can be ascribed to the smaller slope of the
voltage-response for the single-frequency approxima-
tion (Fig. 5C). The voltage responses obtained from
the smoothed DBS pulses of the frequency-dependent
solution underestimated the corresponding VTAs for
the those obtained from the square-wave DBS pulses
by 4.2 % for voltage-controlled stimulation and 1.5 %
for current-controlled stimulation. Since no over-
shooting was noticeable in the voltage responses for
voltage-controlled stimulation, this effect is presum-
ably caused by the slight variation of the slope of the
smoothed DBS pulses compared to the ideal square-
wave DBS pulses. These results suggest that the
slope of the DBS pulse is a more important parame-
ter for the determination of neural activation than the
effect caused by the overshooting of the voltage re-
sponses. To reduce the overshooting while preserving
the slope of the square-wave DBS pulse, a better ap-
proach could be to use the Lanczos sigma approxima-
tion (Lanczos, 1996).
The results of this study are based on various as-
sumptions. The MRI images contain voxel data with
a resolution of 1 mm, i.e. the data is aligned in a
hexahedral mesh, whereas the finite element model
is meshed using tetrahedral elements. This leads to
disconformities between the hexahedral data mesh
and the tetrahedral finite element mesh. To account
for this disconformity, a maximum element length of
0.5 mm for the tetrahedral mesh within the region of
interest was chosen. A better approach could be to
model the important nuclei explicitly, and incorpo-
rate them into the finite element model. However,
generating an explicit representation of all tissue ar-
eas within the brain is still challenging, since the cur-
rent resolution of MRI data often demands a man-
ual segmentation and volume mesh generation. The
results indicate that heterogeneous tissue properties
have only a minor influence on the voltage distribu-
tion and neural activation in the proximity of the STN
in this study, which is noticeable for the computed
thresholds resembling an almost homogeneous spa-
tial distribution (Fig. 7). This minor influence could
be based on the segmented MRI data from the digital
brain atlas, which did not fully render the basal gan-
glia nuclei, resulting in areas of white matter which
are anatomically consistent with gray matter (Rohlf-
ing et al., 2008). MRI data with a more refined seg-
mentation in the region of interest could improve the
rendering of the heterogeneous tissue properties in
this area. Since the mesh disconformities at the tissue
boundaries have only a local influence on the volt-
age response in the proximity of the stimulated tar-
get, it is assumed that this simplification will not in-
SingleFrequencyApproximationofVolumeConductorModelsforDeepBrainStimulationusingEquivalentCircuits
45

fluence a comparison with in vivo practice and that
a precise representation of the spatial tissue distribu-
tion and reliable values for their material parameters
are crucial parameters for computing a realistic VTA.
However, sources for reliable measurement data of
the frequency-dependent electrical properties of bio-
logical tissue are still scarce (Faes et al., 1999). This
lack of data can be attributed to the taxing require-
ments and ethical questions that have to be dealt with
during the realization of experimental studies.
The uncertainty in the electrical properties of
brain tissue and other factors, such as the anisotropy
of brain tissue and the electrode position, can in-
fluence the voltage response and VTA. To quantify
the influence of these uncertainties on the extend of
the VTA, probabilistic methods, such as Monte Carlo
simulation or Polynomial Chaos would be necessary.
The latter method is based on approximating the prob-
abilistic quantities, such as the voltage response and
the VTA, by an expansion on a multi-dimensional
orthogonal polynomial basis of random parameters
(Xiu, 2010). In this case, the computationally ex-
pensive deterministic model is only necessary for the
computation of the coefficients of this polynomial ex-
pansion. This method is already used in various fields
of bio-engineering, such as bio-mechanics (Osnes and
Joakim, 2012) and drug concentration (Preston et al.,
2009), to investigate the influence of uncertainties in
the model parameters. In addition, for problem cases
with only a small number of uncertain parameters, it
is computationally efficient compared to Monte Carlo
simulation (Nobile et al., 2008). However, applica-
tions of this method in bio-electrical engineering are
still scarce.
The neural activation in this study was investi-
gated by the volume of tissue activated for axons
aligned perpendicular to the coronary plane in the
proximity of the stimulated target, which is a widely
accepted method in modelling studies of DBS (Yousif
and Liu, 2009). However, this method simplifies the
reality, since the neurons of the STN are presumably
not evenly oriented and differ in length. Therefore,
the used method used to examine the neural activa-
tion could underestimate the actual stimulated vol-
ume. However, the proposed technique reduces sub-
stantially the computational difficulty of evaluating
the VTA in volume conductor models of DBS. The
extend of the computed VTA and, therefore, the de-
pendence on the parameters observed in this study,
could be validated in vivo by comparing the predicted
activation of adjacent areas to the stimulated target
nucleus, such as the oculomotor nerve, for different
stimulation amplitudes and the observable response
of a patient at these amplitudes (Butson et al., 2006).
The proposed technique for the efficient computa-
tion of the voltage response in the proximity of the
stimulated target in combination with a probabilistic
method based on the Polynomial Chaos can provide
mean values and uncertainty bounds for the simulated
probabilistic voltage response and neural activation,
which could be supportive in in vivo practice, with a
reasonable computational expense.
5 CONCLUSIONS
In this study, the applicability of a single-frequency
approximation of the voltage response based on the
estimation of the electrical properties of brain tissue
at a single frequency in a heterogeneous head model
was investigated. A hybrid method was implemented,
which combines finite element method and equiva-
lent circuits to approximate the transfer function of
the model. Instead of the popular Fourier finite ele-
ment method, which requires the evaluation of several
finite element models, the proposed method allows a
fast computation of the voltage response for voltage-
and current-controlled stimulation by only one eval-
uation of the finite element model plus a minor com-
putational effort in post-processing. The computed
single-frequency approximations of the voltage re-
sponses were in good agreement with the voltage re-
sponses obtained from the frequency-dependent solu-
tions. Furthermore, the frequencies of best approx-
imation resembled approximately the frequencies of
the first dispersive poles of the used brain tissues. The
fast computation of the voltage response allows fur-
ther, more complex, applications such as the sensi-
tivity analysis of uncertain parameters of the model
using probabilistic methods.
ACKNOWLEDGEMENTS
The authors are grateful to DFG (German Science
Foundation) for funding our project in the Research
Training Group 1505/1 ”welisa”. The authors would
like to thank Peadar Grant from the School of Elec-
trical, Electronic & Communications Engineering at
the University College Dublin for his advice on the
volume of tissue activated.
REFERENCES
Bossetti, C. A., Birdno, M. J., and Grill, W. M. (2008).
Analysis of the quasi-static approximation for calcu-
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
46

lating potentials generated by neural stimulation. J
Neural Eng, 5:44–53.
Butson, C. R., Cooper, S. E., Henderson, J. M., and McIn-
tyre, C. C. (2006). Predicting the effects of deep brain
stimulation with diffusion tensor based electric field
models. Med Image Comput Comput Assist Interv,
9:429–437.
Butson, C. R. and McIntyre, C. C. (2005). Tissue and elec-
trode capacitance reduce neural activation volumes
during deep brain stimulation. Clin Neurophysiol,
116:2490–2500.
Cantrell, D. R., Inayat, S., Taflove, A., Ruoff, R. S., and
Troy, J. B. (2008). Incorporation of the electrodeelec-
trolyte interface into finite-element models of metal
microelectrodes. J Neural Eng, 5:54–67.
Faes, T. J. C., van der Meij, H. A., de Munck, J. C., and
Heethaar, R. M. (1999). The electric resistivity of hu-
man tissues (100 Hz–10 MHz): a meta-analysis of re-
view. Physiol Meas, 20:R1–R10.
Gabriel, S., Lau, R. W., and Gabriel, C. (1996). The di-
electric properties of biological tissues: Iii parametric
models for the dielectric spectrum of tissues. Phys
Med Biol, 41:2271–2293.
Grant, P. F. and Lowery, M. M. (2010). Effect of disper-
sive conductivity and permittivity in volume conduc-
tor models of deep brain stimulation. IEEE T Bio-med
Eng, 57:2386–2393.
Grill, W. M. and Mortimer, J. T. (1994). Electrical proper-
ties of implant encapsulation tissue. Ann Biomed Eng,
22:23–33.
Jones, E., Oliphant, T., Peterson, P., et al. (2001). SciPy:
Open source scientific tools for Python.
Kretschmann, H. J. and Weinrich, W. (1991). Klinische
Neuroanatomie und kranielle Bilddiagnostik. Georg
Thieme Verlag, Stuttgart, 2nd edition.
Lanczos, C. (1996). Linear Differential Operators. Siam,
Philadelphia.
McIntyre, C. C., Richardson, A. G., and Grill, W. M.
(2002). Modeling the excitability of mammalian nerve
fibers: Influence of afterpotentials on the recovery cy-
cle. J Neurophysiol, 87:995–1006.
Medtronic, Inc (2003). Medtronic DBS: Lead Kit for Deep
Brain Stimulation.
Montgomery Jr., E. B. and Gale, J. T. (2008). Mechanisms
of action of deep brain stimulation. Neurosci Behav
Rev, 32:388–407.
Nobile, F., Tempone, R., and Webster, C. G. (2008). A
sparse grid stochastic collocation method for partial
differential equations with random input data. SIAM J
Numer Anal, 46(5):2309–2345.
Osnes, H. and Joakim, S. (2012). Uncertainty Analysis of
Ventricular Mechanics Using the Probabilistic Collo-
cation Method. IEEE Trans Biomed Eng, 59:2171–
2179.
Preston, J. S., Tasdizen, T., Terry, C. M., Cheung, A. K.,
and Robert, M. K. (2009). Using the Stochastic Col-
location Method for the Uncertainty Quantification of
Drug Concentration Due to Depot Shape Variability.
IEEE Trans Biomed Eng, 56:609–620.
Rohlfing, T., Zahr, N. M., Sullivan, E. V., and Pfefferbaum,
A. (2008). The sri24 multi-channel brain atlas. Proc
Soc Photo Opt Instrum Eng, 6914:691409.
Schmidt, C. and van Rienen, U. (2012). Modeling the Field
Distribution in Deep Brain Stimulation: The Influence
of Anisotropy of Brain Tissue . IEEE T Bio-med Eng,
59:1583–1592.
Uc, E. Y. and Follet, K. A. (2007). Deep brain stimulation
in movement disorders. Semin Neurol, 27:170–182.
van Rienen, U. (2000). Numerical Methods in Computa-
tional Electrodynamics: Linear Systems in Practical
Applications. Springer, Berlin Heidelberg, 1st edition.
Walckiers, G., Fuchs, B., Thiran, J. P., Mosig, J. R., and
Pollo, C. (2010). Influence of the implanted pulse gen-
erator as reference electrode in finite element model of
monopolar deep brain stimulation. J Neurosci Meth,
186:90–96.
Wei, X. F. and Grill, W. M. (2009). Impedance character-
istics of deep brain stimulation electrodes in vitro and
in vivo. J Neural Eng, 6:046008.
Xiu, D. (2010). Numerical Methods for Stochastic Com-
putations: A Spectral Method Approach. Princeton
University Press.
Yousif, N. and Liu, X. (2009). Investigating the depth
electrode-brain interface in deep brain stimulation us-
ing finite element models with graded compexity in
structure and solution. J Neurosci Meth, 184:142–151.
SingleFrequencyApproximationofVolumeConductorModelsforDeepBrainStimulationusingEquivalentCircuits
47
