
Half Gaussian Kernels Based Shock Filter for
Image Deblurring and Regularization
Baptiste Magnier
1
, Huanyu Xu
2
and Philippe Montesinos
1
1
LGi2P de l’Ecole des Mines d’Al
`
es, Parc scientifique G. Besse, 30035 N
ˆ
ımes cedex 1, France
2
School of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing, China
Keywords:
Shock Filter, Image Regularization, Deblurring, Half Gaussian Kernel.
Abstract:
In this paper, a shock-diffusion model is presented to restore both blurred and noisy image. The proposed
approach uses a half smoothing kernel to get the precise edge directions, and use different shock-diffusion
strategies for different image regions. Experiment results on real images show that the proposed model can ef-
fectively eliminate noise and enhance edges while preserving small objects and corners simultaneously. Com-
pared to other approaches, the proposed method offers both better visual results and qualitative measurements.
1 INTRODUCTION
Image deblurring (Rosenfeld and Kak, 1982) is a pro-
cess of removing unwanted blur in the image. As
image regularization, it is a crucial image process-
ing step in various applications such as remote sens-
ing, medical image processing, computer vision and
so on. They are fields that had largely benefited from
techniques of Partial Differential Equations (PDEs).
PDEs belong to one of the most important part of
mathematical analysis and are closely related to the
physical world (Aubert and Kornprobst, 2006). In
this context, images are considered as evolving func-
tions of time and a regularized image can be seen
as a version of the original image at a special scale.
The advantages of using PDEs in image processing
arise from their well-established theoretical basis and
extensive use in the mathematics, hence allow for a
straightforward extension to image processing tasks.
The non-linear diffusion processes have been
widely used in the last decade in edge preserving de-
noising. In order to regularize a grey level image
I : Ω → R, (Ω ⊂ R
2
) by controlling the diffusion,
with the second derivatives in orthogonal directions
(ξ ⊥ η), respectively in the edge direction called ξ
and in the gradient direction labelled η =
∇I
k∇Ik
, Perona
and Malik (Perona and Malik, 1990) have proposed a
model described by the following equation at time t:
∂I
∂t
= c
ξ
I
ξξ
+ c
η
I
ηη
= c
ξ
∂
2
I
∂ξ
2
+ c
η
∂
2
I
∂η
2
(1)
where c
ξ
and c
η
are coefficients tuning the diffusion.
When c
ξξ
= c
ηη
, the diffusion is isotropic, blurring
important structures in the same way as a convolution
with a Gaussian kernel. Choosing a non-increasing
function of the gradient magnitude g(k∇Ik) such that:
(
c
ξ
= g (k∇Ik) = e
−
k∇Ik
K
2
, K ∈ R
c
η
= g (k∇Ik) + k∇Ik · g
0
(k∇Ik),
(2)
or with g(k∇Ik) =
1
(1+(k∇Ik/K)
2
)
, the diffusion pro-
cess described in eq. 1 can be interpreted as two
directional heat flows with different diffusion inten-
sities depending on the weights (c
ξ
,c
η
) in the η and
ξ directions to preserve discontinuities. This selec-
tive smoothing with edge enhancement performs a
conditional diffusion: when k∇Ik is small, it turns
to a strong smoothing within the homogeneous re-
gions of the image and a weak, selective smoothing
across non-homogeneous ones. When c
η
= 0 in eq.
1, the diffusion scheme behaves like the Mean Cur-
vature Motion (MCM) method:
∂I
∂t
= I
ξξ
, preserving
well edges (Catt
´
e et al., 1992). It consists in perform-
ing the diffusion only along the tangential direction
ξ or along isophotes (i.e. curves of the image sur-
face of constant intensity). Although the approach of
Perona-Malik is able to enhance edges, with highly
noisy images, generally, the noise is not totally re-
moved because the diffusion process is inhibited and
it may generate a lot of undesired artifacts.
The pioneer work of Perona and Malik on
anisotropic diffusion has been one of the most in-
fluential paper in the area. In the same framework,
the seminal contribution of (Osher and Rudin, 1990)
51
Magnier B., Xu H. and Montesinos P..
Half Gaussian Kernels Based Shock Filter for Image Deblurring and Regularization.
DOI: 10.5220/0004224500510060
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 51-60
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

on shock filters concerning image deblurring problem
uses PDEs to enhance edge of the image. Creating
shocks at inflection points, the 2D formulation of the
original shock filter can be formulated as:
∂I
∂t
= −sign(I
ηη
) I
η
(3)
with I
η
= k∇Ik and where:
sign(x) =
1 if I > 0
0 if I = 0
−1 if I < 0
(4)
However, any noise added to the signal creates an in-
finite number of inflection points, disrupting the pro-
cess completely. Hence, in (Alvarez and Mazorra,
1994), the authors replaced the edge detector I
ηη
by
its convolution with the Gaussian function G
σ
, where
σ represents the standard deviation of the Gaussian.
Thus, the filter becomes more robust against noise:
∂I
∂t
= −sign(G
σ
∗ I
ηη
) I
η
. (5)
In order to achieve a complete image restoration pur-
pose, that is deblurring and denoising, Alvarez and
Mazorra try to integrate a denoising component into
the existing shock filter deblurring model (Alvarez
and Mazorra, 1994). Coupling diffusion (I
ξξ
term)
and shock filter, this approach is modeled as:
∂I
∂t
= C I
ξξ
− sign(G
σ
∗ I
ηη
) sign(G
σ
∗ I
η
) I
η
(6)
where C is a strictly positive constant and ξ is the con-
tour direction, used as a balance between anisotropic
diffusion behavior and shock effect. Thus,in addi-
tion to create shocks at inflection points, the Alvarez-
Mazorra shock filter model diffuses in the edge direc-
tion, eliminating noise.
In (Kornprobst et al., 1997) authors extended the
above strategy and proposed a combined diffusion-
reaction-coupling model, this filter uses:
• a diffusion term according to the MCM scheme,
• a reaction term based on the theory of shock filters
(Osher and Rudin, 1990),
• a coupling term that keeps the solution close to the
original image.
Although Alvarez-Mazorra and Kornprobst et al.
shock filters can eliminate the noise when deblurring,
it created homogeneous blobs in flat noisy regions that
affect the visual appearance. Moreover, the authors
noticed both in (Kornprobst et al., 1997) and (Korn-
probst et al., 1997), after a certain number of itera-
tions, corner smoothing is produced.
In (Weickert, 2003), the Coherence-Enhancing
Shock Filters (CESF) model was proposed, it is the
combination of the Coherence-Enhancing Diffusion
(CED) in (Weickert, 1999) model and the shock fil-
ter theory (eq. 3). The coherence enhancement ef-
fect is achieved by steering the shock filtering along
the directions yielded by J
ρ
(∇I) = G
ρ
∗ (∇I · ∇I
T
), a
structure tensor, where G
ρ
represents a Gaussian ker-
nel of standard deviation ρ. Using ω the normalized
eigenvector corresponding to the largest eigenvalue
that describes the direction where the contrast change
is maximal, the CESF is defined as follows:
∂I
∂t
= −sign ((G
σ
∗ I)
ωω
) k∇Ik (7)
The CESF model behaves like a contrast enhanc-
ing shock filter, it enhances well strip structures like
the fingerprint images, however creates artificial lines
when dealing with noisy or natural images.
Motivated by quantum mechanics and
Schrodinger equation, Gilboa proposed in (Gilboa
et al., 2004) a generalized complex shock filter for
image deblurring and denoising. Based on a complex
diffusion term Λ regularizing the noise and indicating
inflection points, the imaginary value of the solution
controls the smoothing process defined as follows:
∂I
∂t
= −
2
π
arctan
a Im
I
θ
I
η
+ ΛI
ηη
+
˜
ΛI
ξξ
(8)
where (a,
˜
Λ) are real constants and θ is close to zero.
Nevertheless this method brings a weak edges en-
hancement because this filter operates as a diffusion
process for a small time whereas shock terms are cre-
ated for a large time which can blur some edges.
In (Fu et al., 2006), the authors have developed a
region-based shock-diffusion scheme. Using a Guas-
sian kernel, the authors divide the image into three-
type regions by its smoothed gradient magnitude. For
high gradients (such as boundaries of different ob-
jects), a shock-type backward diffusion is performed
in the gradient direction, and incorporating a forward
diffusion in the isophote lines. For medium gradients
(such as textures and details), a soft shock-type back-
ward diffusion is performed. Concerning small gradi-
ents (such as smoother segments inside different areas
or flat regions), an isotropic diffusion is applied:
∂I
∂t
= c
1
I
ξξ
− sign(G
σ
∗ I
ηη
) I
η
, if k∇Ik > T
1
∂I
∂t
= c
1
I
ξξ
− c
2
sign(G
σ
∗ I
ηη
) I
η
,
if T
1
> k∇Ik > T
2
∂I
∂t
= ∆I = I
ξξ
+ I
ηη
eslewhere
(9)
with c
1
=
1
1+ζ
1
·I
2
ξξ
and c
2
= |th(ζ
2
· I
ηη
)|. The
parameters are chosen according to different image
regions, (ζ
1
,ζ
2
) are constants, and (T
1
,T
2
) are two
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
52

gradient thresholds. Different from a sigmoid func-
tion, the hyperbolic tangent function th(x) guaran-
tees a gradual smoothing transition in areas having
medium gradient (T
1
> k∇Ik > T
2
). Note that the
1
1+l
1
·I
2
ξξ
term enables to control the diffusion at high
curvature edges (Harris and Stephens, 1988), while
preserving corners. This shock filter is able to elimi-
nate the noise successfully, but at sharp edges of the
restored image is too strong to preserve the original
information.
In this paper, we propose a new PDE that com-
bines shock filter with an edge detector using a half
Gaussian kernel. The contour detection step brings a
more precise direction of the gradient than shock fil-
ters using isotropic Gaussian kernels, thus it preserves
better corners and small objects of the image. More-
over, the model can solve both deblurring and denois-
ing with both diffusion and the shock filter term.
2 A GRADIENT EXTRACTION
AND TWO EDGE DIRECTIONS
ESTIMATION
Steerable isotropic filters (Freeman and Adelson,
1991; Jacob and Unser, 2004) or anisotropic edge de-
tectors (Perona, 1992) perform well in detecting large
linear structures (represented in Fig. 1(a) and (b)).
Close to corners however, the gradient magnitude de-
creases as the edge information under the scope of the
filter decreases. Consequently, the robustness to noise
concerning small objects becomes inappropriate.
A simple solution to bypass this effect is to con-
sider paths crossing each pixel in several directions
as in (Sha’ashua and Ullman, 1988). Wedge steer-
able filters introduced by Simoncelli and Farid (Si-
moncelli and Farid, 1996) are composed of asymmet-
ric masks providing orientation of edges in different
directions issued from a pixel. Unlike the Gaussian
function, which is an optimal solution for the Canny
criteria(Canny, 1986), wedge steerable filters have a
constant amplitude on almost the whole extent of the
mask. The idea developed in (Montesinos and Mag-
nier, 2010) was to split the derivative (and smoothing)
anisotropic Gaussian kernel in two parts: a first part
(a) Isotropic gaus-
sian kernel
(b) Anisotropic
gaussian kernel
(c) Half anisotropic
gaussian kernel
Figure 1: Different 2D derivative Gaussian kernels.
along an initial direction, and a second part along a
second direction (represented in Fig. 4 (a)). At each
pixel of coordinates (x,y), a derivation filter is applied
to obtain a derivative information Q (x, y,θ) in func-
tion of the orientation θ ∈ [0; 2π[ :
Q (x,y, θ) = I
θ
∗C · H (−y) · x · e
−
x
2
2λ
2
+
y
2
2µ
2
(10)
where I
θ
corresponds to a rotated image
1
of orienta-
tion θ, C is a normalization coefficient, (x,y) are pixel
coordinates, and (µ,λ) the standard deviations of the
anisotropic Gaussian filter. Since we only require the
causal part of this filter along Y axis, we simply “cut”
the smoothing kernel by the middle, in an operation
that corresponds to the Heaviside function H.
This filter can be compared with isotropic and
full anisotropic derivative Gaussian kernels in Fig. 1.
Q (x,y, θ) represents the slope of a line derived from a
pixel in the perpendicular direction to θ (see Fig. 2(b)
for several Q (x,y,θ) signals). We can note that simi-
lar filters can also be used for the matching of interest
points (Palomares et al., 2012).
To obtain a gradient k∇Ik and its associated direc-
tion η on each pixel, we first compute with θ
1
and θ
2
the global extrema of the function Q (x, y,θ). θ
1
and
θ
2
define a curve crossing the pixel (an incoming and
outgoing direction). Two of these global extrema can
then be combined to maximize k∇Ik, i.e. :
k∇Ik = max
θ∈[0,2π[
Q (x,y, θ) − min
θ∈[0,2π[
Q (x,y, θ)
θ
1
= argmax
θ∈[0,2π[
(Q (x,y, θ))
θ
2
= argmin
θ∈[0,2π[
(Q (x,y, θ))
(11)
Fig. 3 shows a gradient image obtained using half
Gaussian kernels. Once k∇Ik, θ
1
and θ
2
have been
obtained, the edges can be easily extracted by com-
puting local maxima of k∇Ik in the direction of the
angle η (Fig. 2(c) and 4) corresponding to the angle
bisector between the two directions (θ
1
,θ
2
):
η =
θ
1
+ θ
2
2
. (12)
Then, a binary image can be built using an hystere-
sis threshold (see (Montesinos and Magnier, 2010) for
further details). In this paper, we are solely interested
by the gradient magnitude, the angle formed by the
two orientations (θ
1
,θ
2
) and the directions (η ⊥ ξ),
represented in the diagram in Fig. 4, used in our dif-
fusion scheme discussed below. Moreover, as shown
1
As explained in (Montesinos and Magnier, 2010), the
image is oriented instead of the filter so as to increase algo-
rithmic complexity and moreover allows use of a recursive
Gaussian filter (Deriche, 1992).
HalfGaussianKernelsBasedShockFilterforImageDeblurringandRegularization
53

+
+
+
+
+
+
+
+
+
+
+
+
1
4
3
5
6
1
4
3
6
2
(a) Points selection
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 1
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 2
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 3
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 4
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 5
0 100 200 300
−0.1
−0.05
0
0.05
0.1
Point 6
(b) Q (x,y,θ) for each points of (a)
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
0
360
1
2
Discretized angle (degrees)
Quality function
l
l
l
90
180
270
l
_
(c) Example of a Q (x,y,θ) function
Figure 2: Points selection and its associated Q (x,y, θ), µ = 10, λ = 1 and ∆θ =
π
90
. Note that the initial orientation of the filter
is vertical, upwardly directed and steerable clockwise. In (b), the X axis represents the filter direction in degrees.
(a) Real noisy image containing high
noise 508×440
(b) Gradient image µ = 5, λ = 1,
∆θ =
π
90
Figure 3: Gradient image (normalized negative image).
Figure 4: Directions of our diffusion scheme.
in Fig. 5, half Gaussian kernels enable to extract
two precise directions on blurred edges (orientations
where the positive and respectively negative slopes
are maximum or minimal). Issued from these orienta-
tions, diffusion directions (η,ξ) are also precise.
Finally, due to their thinness, rotating filters en-
able computing two precise diffusion orientations in
the edge directions, even at high noise levels (Magnier
et al., 2012). In (Magnier et al., 2011a), the authors
have evaluated the edge detection used in this method
with a strong noise level and a comparison with other
approaches (Deriche, 1992; Perona, 1992) shows the
efficiency of this method.
3 SIGMOIDS BASED SHOCK
FILTER FOR REGIONS
Images are composed of different regions and fea-
tures. These regions could be texture or homogeneous
image parts. Image enhancing and smoothing are op-
posite processes, hence, these different parts of the
images should be treated differently to obtain the bet-
ter result. In our shock-diffusion scheme, we divide
an image into three-type regions using its gradient
magnitude (eq. 11).
Thus, we insert two control functions in our dif-
fusion scheme, which both depend on the gradient
magnitude and the angle between the two edge orien-
tations (eq. 11) which is labelled β = (θ
1
− θ
2
). This
β angle and the η direction are diagramed in Fig. 6.
Concerning high gradients (i.e. greater than a thresh-
old τ
1
), the image is diffused in the tangential direc-
tion of edges ξ and a the regularizing process creates
a shock in the η direction. If the gradient is smaller,
in addition to a forward smoothing in the direction
ξ, a shock-type backward and a forward diffusion are
performed in the η direction both in function of the
gradient level and β. In the remainder of the image
(i.e. low gradient), we apply an isotropic diffusion,
smoothing small details as noise in homogeneous re-
gions. Inspired by (Magnier et al., 2012), (Magnier
et al., 2011b) and (Fu et al., 2006), involving the gra-
dient value and the β angle, we present in the follow-
ing formula our shock-diffusion equation:
∂I
∂t
= f
k
· I
ξξ
− f
k
· sign(I
ηη
) · I
η
,
for k∇Ik > τ
1
∂I
∂t
= f
k
· I
ξξ
+ f
h
· I
ηη
− f
k
· sign(I
ηη
) · I
η
for τ
1
> k∇Ik > τ
2
∂I
∂t
= ∆I = I
ξξ
+ I
ηη
eslewhere
(13)
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
54

0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
(a) Original image (b) σ = 1 (c)σ = 2 (d)σ = 3 (e) σ = 4
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
0 //4 //2 3//4 / 5//4 3//2 7//4 2/
<0.2
<0.1
0
0.1
0.2
(f) σ = 5 (g) σ = 6 (h) σ = 7 (i) σ = 8 (j)σ = 9
Figure 5: Q signals on a pixel positioned on a step edge in the center of the image in function of the level of a Gaussian blur
of standard deviation σ. The initial orientation of the filter is vertical, upwardly directed and steerable clockwise, with λ = 1,
µ = 5 and ∆θ =
π
90
. The maximum of the crests and the minimum of the valleys indicate the orientations of the edges.
with (τ
1
,τ
2
) two gradient thresholds (τ
1
> τ
2
),
f
k
(k∇Ik,β) =
e
−
k∇Ik
k
+ e
−
π−β
π·k
2
, k ∈ ]0,1]
f
h
(k∇Ik,β) =
e
−
k∇Ik
h
+ e
−
π−β
π·h
2
, h ∈ ]0,1].
(14)
and we impose k>h so that f
k
(k∇Ik,β)> f
h
(k∇Ik,β).
In order to ensure a progressive diffusion, f
k,h
are sig-
moids functions, they are represented in Fig. 6.
Note that thresholds (τ
1
,τ
2
) are applied only on
the gradient magnitude and not a combination with
the β angle. In fact, a threshold also on the β angle
would create shocks, resulting in undesirable artifacts
in some image parts (e.g. in homogeneous regions).
0
0.2
0.4
0.6
0.8
1
0
//2
/
3//2
2/
0
0.5
1
`
|¢ I |
Figure 6: β angle, η direction, bisector of (θ
1
,θ
2
) and the
control function f
k
with k = 0.3.
4 EXPERIMENTAL RESULTS
To illustrate the effective of the proposed shock fil-
ter with edge detector using a half Gaussian ker-
nels, we present some experimental results . We
compare the proposed shock filter with the original
one (OR), Alvarez-Mazorra (AM), Gilboa, Weickert
(CESF) and Fu et al. (Fu) approaches. Most of the
tested images contain blur and noise. In order to mea-
sure the objective performance of these models, we
compute the PSNR (Peak Signal to Noise Ratio) and
the SSIM (Structural SIMilarity presented in (Wang
et al., 2004)) before compare each results.
We choose the most suitable parameters for each
models. In order to obtain comparative results, we
choose the same larger (i.e. standard deviation) of
the Gaussian for approaches using this function (i.
e. σ = µ = 1). For the original shock filter, dt =
0.2 and Alvarez-Mazorra approach, dt = 0.1, C = 1,
σ = 1. Parameters used in the Gilboa shock filter are
dt = 0.1, Λ = 0.2,
˜
Λ = 0.4, a = 2, θ = pi/1000 and
σ = 1. For the CESF model, σ = 1, ρ = 1. Concern-
ing algorithm of Fu et al., dt = 0.05, T
1
= 15, T
2
= 5,
ζ
1
= 0.0008, ζ
2
= 300 and σ = 1. In our method,
dt = 0.05, µ = 5, λ = 1, ∆θ =
π
90
and (k, h) are change-
able in function of the structures of the treated images.
HalfGaussianKernelsBasedShockFilterforImageDeblurringandRegularization
55

(a) Original Cameraman image
256×256
(b) Blurred and noised image,
PSNR=23.71, SSIM=0.512
(c) Original shock filter,
iterations = 30, PSNR=22.07, SSIM=0.420
(d) Alvarez-Mazorra shock filter,
iteration = 50, PSNR=22.72, SSIM=0.715
(e) Gilboa complex shock filter,
iteration = 30, PSNR=22.92, SSIM=0.740
(f) CESF, iteration = 30,
PSNR=19.91, SSIM=0.373
(g) Perona-Malik diffusion, K = 0.02,
iteration = 500, PSNR=22.72, SSIM=0.715
(h) Fu shock filter,
iteration = 30, PSNR=24.38, SSIM=0.776
(i) Proposed shock filter,
iteration = 20, PSNR=25.82, SSIM=0.792
0 10 20 30 40 50 60 70 80 90 100
20
21
22
23
24
25
26
iterations
PSNR
Proposed
Fu
OR
AM
Gilboa
degraded image
(j) PSNR representation as a function of the number of iterations. (k) SSIM representation as a function of the number of iterations.
Figure 7: Restoration of Cameraman image by different methods.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
56
In the two first results, noisy images are produced
by adding random Gaussian noise and the blur is
caused with the convolution of a Gaussian kernel of
standard deviation of σ.
First, we use a Cameraman image blurred (σ = 1)
and noised (σ = 10) to compare the performance of
the different models (Fig. (7)). The original shock
filter and the Perona-Malik method have not very de-
blurred the image and can not eliminate the noise ef-
fectively. AM approach created homogeneous blobs
and lost most details. Gilboa filter can smooth the
noise, but does not preserve the details of the im-
age (especially in the background). The CESF model
performs bad in natural images in noise removal and
creates artificial strips. Method of Fu et al. has suc-
cessfully eliminated the noise, nevertheless, the shock
at the edges of the restored image is too strong to
preserve the original information so that the result
looks like a synthetic image. The proposed model
(Fig. 7(i)) eliminates the noise effectively and bet-
ter enhances the edges than other previous methods
as small objects visible in the background. Finally,
curves indicate in Figs. 7(j) and (k) that compared to
other models, the proposed method can get the high-
est value both in PSNR and SSIM.
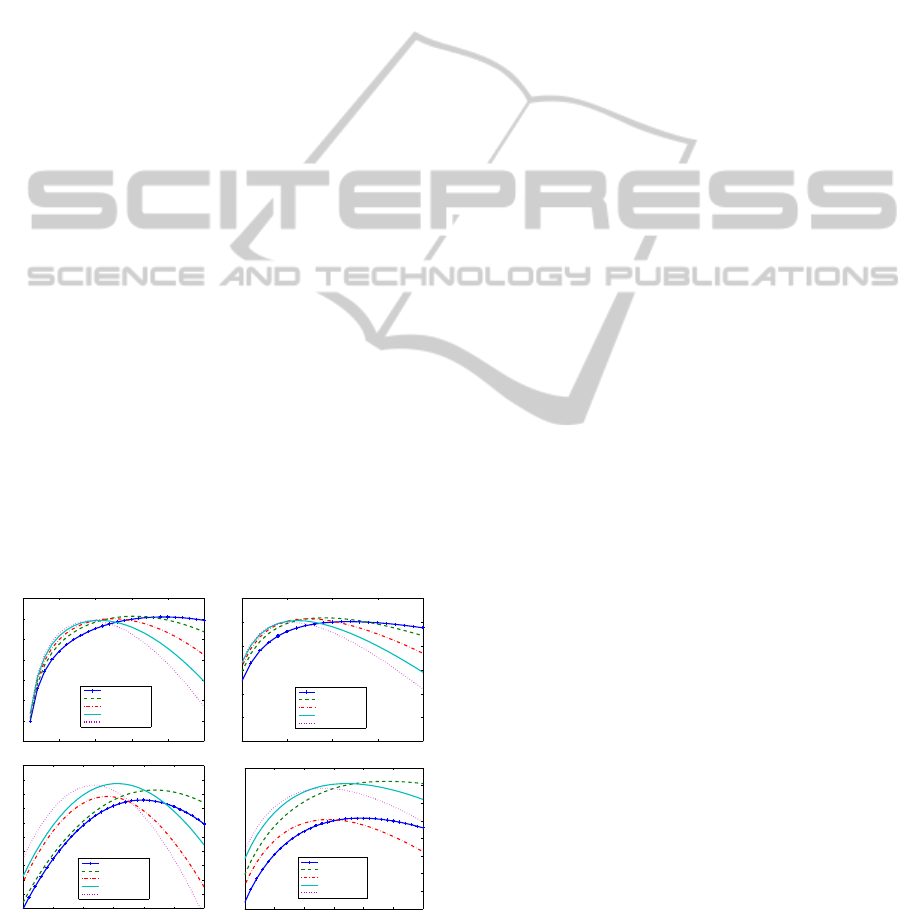
In order to choose better (k, h) parameters of our
proposed method, Fig. 8 shows PSNR and SSIM
representation of Cameraman image as a function of
the iterations number using different values of (k,h).
From the curves, we can determine the choice of
the ideal game of parameters. For this Cameraman
image, blurred and noised, the curves indicate that
k = 0.2 and h = 0.1 are the best choice for eq. 14.
Moreover, this picture is not so blurred, as the diffu-
sion model is different in function of the two gradient
0 5 10 15 20 25
24.6
24.8
25
25.2
25.4
25.6
25.8
26
Iterations
PSNR
k = 0.2 and h = 0.1
k = 0.3 and h = 0.1
k = 0.4 and h = 0.1
k = 0.5 and h = 0.1
k = 0.6 and h = 0.1
5 10 15 20 25
0.74
0.75
0.76
0.77
0.78
0.79
0.8
Iterations
ssim
k = 0.2 and h = 0.1
k = 0.3 and h = 0.1
k = 0.4 and h = 0.1
k = 0.5 and h = 0.1
k = 0.6 and h = 0.1
10 15 20 25 30 35 40
27.5
27.6
27.7
27.8
27.9
28
28.1
28.2
28.3
28.4
28.5
Iterations
PSNR
k = 0.3 and h = 0.1
k = 0.3 and h = 0.2
k = 0.4 and h = 0.1
k = 0.4 and h = 0.2
k = 0.5 and h = 0.2
10 15 20 25 30 35 40
0.75
0.755
0.76
0.765
0.77
0.775
0.78
0.785
0.79
Iterations
ssim
k = 0.3 and h = 0.1
k = 0.3 and h = 0.2
k = 0.4 and h = 0.1
k = 0.4 and h = 0.2
k = 0.5 and h = 0.2
(a) PSNR representation. (b) SSIM representation.
Figure 8: PSNR and SSIM representation of Cameraman
(top) and House (bottom) images as a function of the itera-
tions number with different games of parameters (k, h).
thresholds (τ
1
,τ
2
), these two values must not be so
high to enhance small objects: (τ
1
,τ
2
) = (0.1,0.15).
The next picture in Fig. (9) concerns the House
image corrupted by a Gaussian blur (σ = 2) and a
Gaussian noise (σ = 10). Comparing different meth-
ods, the conclusion is the same as the experiments of
Cameraman. There are not much texture and small
objects in this image, so that methods of Gilboa and
Fu et al. can achieve good results. However, the edges
of the restored images seem unnatural. Our result has
a better visual appearance and small object are better
enhanced. Lastly, curves indicate in Figs. 9(j) and (k)
that compared to other models, the proposed method
can get the highest value both in PSNR and SSIM for
this blurred image.
Fig. (8) shows PSNR and SSIM representation of
the corrupted House image as a function of the iter-
ations number with different values of (k,h). Curves
indicate that k = 0.4 and h = 0.2 are the best choice
for this image. As this image is more blurred than the
Cameraman image, the k value is greater than the pre-
vious result. Actually, the more the image is blurred,
the more the parameter k in the f
k
function (eq. 14)
must be elevated in order to drive the shock term and
diffuse in the ξ direction, enhancing edges. We chose
(τ
1
,τ
2
) = (0.5,0.1) for this result because this image
is more blurred than the Cameraman image and im-
portant structures have high normalized gradient.
To verify the effectiveness of the proposed model,
we also tested our algorithm on a natural degenerated
image (Fig. (10)). Compared to other methods, the
proposed approach has the best noise removal result
and can preserve the contrast of the original image.
Moreover, edges are sharped with our method, it is
better visible on the enlargement. These different en-
largements of AM and Fu show most homogeneous
blobs whereas our results preserve much details while
removing efficiently the noise. (τ
1
,τ
2
) = (0.2,0.1)
for our result with τ
1
greater than in the Cameraman
image because the considerate image contains a high
noise which is not correctly diffused with a lower
value of τ
1
. The choice (k,h) = (0.3,0.1) is done be-
cause this image is not so blurred, as the Cameraman.
In order to show the coherence of our algorithm,
we apply our diffusion scheme on a fingerprint image.
Here, we use µ = 10, λ = 1 to obtain a longer filter
such that the algorithm prolongs stripes. We com-
pare our result with the CESF model in Fig. (11).
After 300 iterations, our result contains more pro-
longed filaments and sharped edges show the coher-
ence and the stability of our diffusion scheme. In
order to strongly extend lines, (k,h) = (0.6, 0.2) and
(τ
1
,τ
2
) = (0.1,0.05) are relatively low because this
image does not contain any noise.
HalfGaussianKernelsBasedShockFilterforImageDeblurringandRegularization
57

(a) Original House image
256×256
(b) Blurred and noised image,
PSNR=23.53, SSIM=0.436
(c) Original shock filter,
iteration = 30, PSNR=22.93, SSIM=0.396
(d) Alvarez-Mazorra shock filter,
iteration = 50, PSNR=25.52, SSIM=0.734
(e) Gilboa complex shock filter,
iteration = 30, PSNR=25.63, SSIM=0.767
(f) CESF, iteration = 30, PSNR=21.53,
SSIM=0.347
(g) Perona-Malik diffusion, K = 0.02,
iteration = 500, PSNR=22.72, SSIM=0.715
(h) Fu shock filter,
iteration = 30, PSNR=24.38, SSIM=0.776
(i) Proposed shock filter,
iteration = 25, PSNR=26.87, SSIM=0.781
0 10 20 30 40 50 60 70 80 90 100
20
21
22
23
24
25
26
27
28
iterations
PSNR
Proposed
Fu
OR
AM
Gilboa
degraded image
(j) PSNR representation as a function of the number of iterations. (k) SSIM representation as a function of the number of iterations.
Figure 9: Restoration of House image by different methods.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
58

(a) Real degenerated image
508×445
(b) Original shock filter,
iteration = 30
(c) Alvarez-Mazorra shock filter,
iteration = 50
(d) Gilboa complex shock filter,
iteration = 30
(e) CESF,
iteration = 30
(f) Fu shock filter,
iteration = 30
(g) Magnier et al. scheme (Magnier et al., 2012)
iteration = 15
(h) Our result,
iteration = 50
(i) Our result,
iteration = 100
(j) Enlargement of (a) (k) Enlargement of (c) (l) Enlargement of (f) (m) Enlargement of (i)
Figure 10: Restoration of real degenerated image by different methods.
5 CONCLUSIONS
In this paper, we have presented a new shock-
diffusion filter to restore blurred and noisy image. To
make it more efficient, we have introduced new con-
trol functions which enable a diffusion process en-
hancing both edges and corners in the image. The
main advantages of our method is that it is based on
half Gaussian kernels, extracting precisely the edge
directions which enables a preservation of small ob-
HalfGaussianKernelsBasedShockFilterforImageDeblurringandRegularization
59

(a) Original fingerprint image, 368×600 (b) CESF, iteration = 300 (c) Proposed shock filter, iteration = 300
Figure 11: Regularization of a fingerprint image.
jects. Finally, the proposed model uses different
shock-diffusion strategies on different parts of the
image to efficiently eliminate the noise and enhance
edges. Experiments on blurred and natural images
show that the proposed model can remove noise and
sharpen edges effectively, while preserving small ob-
jects and corners of the image. As shown in a fin-
gerprint image, this approach is a coherence diffusion
method, keeping also the contrast, thus produces bet-
ter visual quality than the compared models.
REFERENCES
Alvarez, L. and Mazorra, L. (1994). Signal and image
restoration using shock filters and anisotropic diffu-
sion. SIAM J. Numer. Anal., 31(2):590–605.
Aubert, G. and Kornprobst, P. (2006). Mathematical prob-
lems in image processing: partial differential equa-
tions and the calculus of variations (second edition),
volume 147. Springer-Verlag.
Canny, F. (1986). A computational approach to edge detec-
tion. IEEE TPAMI, 8(6):679–698.
Catt
´
e, F., Lions, P., Morel, J., and Coll, T. (1992). Image
selective smoothing and edge detection by nonlinear
diffusion. SIAM J. of Num. Anal., pages 182–193.
Deriche, R. (1992). Recursively implementing the gaussian
and its derivatives. In ICIP, pages 263–267.
Freeman, W. T. and Adelson, E. H. (1991). The design and
use of steerable filters. IEEE TPAMI, 13:891–906.
Fu, S., Ruan, Q., Wang, W., and Chen, J. (2006). Region-
based shock-diffusion equation for adaptive image en-
hancement. Advances in Machine Vision, Image Pro-
cessing, and Pattern Analysis, pages 387–395.
Gilboa, G., Sochen, N., and Zeevi, Y. Y. (2004). Im-
age enhancement and denoising by complex diffusion
processes. IEEE Trans. Pattern Anal. Mach. Intell.,
26(8):1020–1036.
Harris, C. and Stephens, M. (1988). A combined corner and
edge detector. In Alvey vision conference, volume 15,
page 50. Manchester, UK.
Jacob, M. and Unser, M. (2004). Design of steerable filters
for feature detection using canny-like criteria. IEEE
TPAMI, 26(8):1007–1019.
Kornprobst, P., Deriche, R., and Aubert, G. (1997). Image
coupling, restoration and enhancement via pde’s. Im-
age Processing, International Conference on, 2:458.
Magnier, B., Montesinos, P., and Diep, D. (2011a). Fast
Anisotropic Edge Detection Using Gamma Correction
in Color Images. In IEEE 7th ISPA, pages 212–217.
Magnier, B., Montesinos, P., and Diep, D. (2011b). Texture
Removal in Color Images by Anisotropic Diffusion.
In VISAPP, pages 40–50.
Magnier, B., Montesinos, P., and Diep, D. (2012). A new
region-based pde for perceptual image restoration. In
VISAPP, pages 56–65.
Montesinos, P. and Magnier, B. (2010). A New Perceptual
Edge Detector in Color Images. In ACIVS, volume 2,
pages 209–220.
Osher, S. and Rudin, L. I. (1990). Feature-oriented im-
age enhancement using shock filters. SIAM J. Numer.
Anal., 27(4):919–940.
Palomares, J. L., Montesinos, P., and Diep, D. (2012). A
New Affine Invariant Method for Image Matching. In
IEEE SPIE (3DIP), volume 8290, page 82900Q.
Perona, P. (1992). Steerable-scalable kernels for edge detec-
tion and junction analysis. IMAVIS, 10(10):663–672.
Perona, P. and Malik, J. (1990). Scale-space and edge
detection using anisotropic diffusion. IEEE TPAMI,
12:629–639.
Rosenfeld, A. and Kak, A. C. (1982). Digital Picture Pro-
cessing. Academic Press, Inc., Orlando, FL, USA,
2nd edition.
Sha’ashua, A. and Ullman, S. (1988). Structural Saliency:
The Detection of Globally Salient Structures Using
Locally Connected Network. In ICCV, pages 321–
327.
Simoncelli, E. and Farid, H. (1996). Steerable wedge filters
for local orientation analysis. IEEE TIP, 5(9):1377–
1382.
Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).
Image quality assessment: From error visibility to
structural similarity. IEEE TIP, 13(4):600–612.
Weickert, J. (1999). Coherence-enhancing diffusion filter-
ing. IJCV, 31(2):111–127.
Weickert, J. (2003). Coherence-enhancing shock filters.
In Lecture Notes in Computer Science, pages 1–8.
Springer.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
60
