A Tool for Brain Magnetic Resonance Image Segmentation
Baptiste Magnier, Philippe Montesinos and Daniel Diep
LGi2P de l’Ecole des Mines d’Al
`
es, Parc Scientifique G. Besse, 30035 N
ˆ
ımes Cedex 1, France
Keywords:
Brain MRI Regularization,Edge Detection, Rotating Filters, Anisotropic Diffusion.
Abstract:
This paper is dedicated to a brain magnetic resonance images regularization method, preserving grey/white
matter edges using rotating smoothing filters. After a preprocessing, the originality of this approach resides in
the mixing of ideas coming both from pixel classification which determines roughly if a pixel belongs to a ho-
mogenous region or an edge and an anisotropic edge detector which computes two precise diffusion directions.
These directions are used by an anisotropic diffusion scheme which is accurately controlled near edges and
corners. Comparing our results with existing algorithms allows us to validate the robustness of our method.
1 INTRODUCTION
Image segmentation is a key task in many medi-
cal applications. Brain Magnetic Resonance Images
(MRI) segmentation is quite complicated and chal-
lenging (Klauschen et al., 2009). Its accurate segmen-
tation is very important for detecting tumors, edema,
necrotic tissues or various diseases (Alzeimer, hydro-
cephaly...). A quantity of methods for automatic and
semi-automatic image segmentation exists, most of
them fail because of unknown noise, poor contrast, ar-
tifacts due to movements and weak boundaries. Brain
MRI regularization must make possible to largely im-
prove the diagnosis or the quantification of neural de-
fects and diseases. However, in most of these images,
the noise is an obstacle of the regularization.
In this paper, we propose a method removing the
noise enhancing edges between the grey and the white
matter. After a transformation of the pixel inten-
sities distribution, we apply a method consisting in
the regularization of the image according to a clas-
sification of white/grey matter edges. We consider
a diffusion process driven by a partial differential
equation (PDE) (Aubert and Kornprobst, 2006). In
cases of homogeneous region, the purpose is to dif-
fuse isotropically removing the noise from the im-
age. Otherwise, in case of a contour region, we apply
an anisotropic diffusion. Unlike several other diffu-
sion scheme (Alvarez et al., 1992) (Weickert, 1999)
(Tschumperl
´
e, 2006), our control function does not
solely depend on the image gradient but instead on a
pre-established classification map of the initial image.
Moreover in (Alvarez et al., 1992) (Weickert, 1999)
(Tschumperl
´
e, 2006), only one direction is consid-
ered at edges and corner points, which has the effect
of rounding small structures, especially when the pa-
rameter σ used for the gradient estimation is large (a
σ value too large blurs also edges of grey/white mat-
ters). Consequently, these schemes behave like the
MCM scheme (Catt
´
e et al., 1995), e.g. which rounds
corners after a certain number of iterations. Further-
more, when the anisotropic coefficient is too large for
tensorial approaches (Weickert, 1999) (Tschumperl
´
e,
2006), the diffusion of a high noise brings a fiber ef-
fect in homogeneous regions. In order to minimize
this effect and accurately localize edges, contours
junctions or corners, we considered the two directions
issued from edges only in contours regions (Magnier
et al., 2011b). This diffusion scheme is tuned both by
the gradient magnitude and the angle between these
two directions (Magnier et al., 2012).
2 A ENHANCED
SEGMENTATION METHOD
This section presents the robust and efficient segmen-
tation approach proposed for the effective segmenta-
tion of noisy brain MRI images. The approach is com-
posed of three steps:
1. Gamma Correction: we use a preprocessing of the
images by gamma correction in order to expand
the histogram in the range of intensities that char-
acterizes the regions of interest (i.e. white and
grey matter).
75
Magnier B., Montesinos P. and Diep D..
A Tool for Brain Magnetic Resonance Image Segmentation.
DOI: 10.5220/0004224600750079
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 75-79
ISBN: 978-989-8565-48-8
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2. Edge and Region Classification: using a rotating
smoothing filter, we provide a method to classify
each pixel of an image into edge or region class.
3. Anisotropic Diffusion: in order to enhance the de-
tected features, we apply two types of diffusion
in the image, depending on the class detected:
within a region class, an isotropic diffusion is ap-
plied and in edge class, involving a rotating Gaus-
sian derivative half-filter, we extract a gradient
and two directions of edges, then we apply an
anisotropic diffusion along these two directions.
In brain MRI images, white and grey matters are
often dfficult to distinguish, in order to overcome this
problem, we use gamma correction on the original im-
age. Gamma correction is the name of a nonlinear op-
eration which modifies pixel intensities in images. It
can be used to improve the contrast in parts of an im-
age, and compensate for human perception by modi-
fying the allocation of bits used by the image coding
(Poynton, 1996) (Magnier et al., 2011a). Gamma cor-
rection is defined as follows: I
out
(P) = (I(P))
γ
, with
γ > 0 and I(P) ∈ [0,1], where I(P) and I
out
(P) are
respectively the input and output normalized pixel in-
tensities.
γ > 1 leads to a darker image whereas γ < 1 leads
to a brighter image. As the aim is to enhance edges
between the white and the grey matter, we use γ > 1,
this operation enhances the limit between the white
and the grey matters but enhances also the noise.
However, our method is sufficiently robust to han-
dle noisy images due to the thinness of the direc-
tional Gaussian filters (Magnier et al., 2011a) (Mag-
nier et al., 2012).
3 A EDGE/REGION CLASSIFIER
USING HALF SMOOTHING
FILTERS
In the edge classification phase, the whole image is
filtered by a rotating half smoothing filter in the di-
rection θ:
G
(µ,λ)
(x,y,θ) = C · I
θ
∗ H (−y) ·e
−(x
2
/2λ
2
+ y
2
/2µ
2
)
(1)
where I
θ
corresponds to a rotated image
1
of orienta-
tion θ, C is a normalization coefficient, (x,y) are pixel
coordinates, and (µ, λ) the standard deviations of the
anisotropic Gaussian filter. Since we only require the
1
As explained in (Montesinos and Magnier, 2010), the
image is oriented instead of the filter so as to increase algo-
rithmic complexity and moreover allows use of a recursive
Gaussian filter (Deriche, 1992).
causal part of this filter along Y axis, we simply “cut”
the smoothing kernel by the middle, in an operation
that corresponds to the Heaviside function H.
Developped by (Montesinos and Magnier, 2010),
this filter has proven to be easily implemented and
adaptable to different application objectives, such
as edge detection (Montesinos and Magnier, 2010)
(Magnier et al., 2011a), texture suppression (Magnier
et al., 2011b) and image restoration (Magnier et al.,
2012). Applying this rotating filter in a 360
◦
scan
to each point of an image leads to a point descriptor
which represents the filtered intensity along all direc-
tions. The analysis of the descriptor enables to clas-
sify each point in two classes: flat areas (i.e. angu-
lar sector > 30
◦
estimated from de first derivative of
s(θ) and a threshold s
th
) are associated to homoge-
nous regions, whereas edges are characterized by a
non-smooth descriptor.
4 TWO EDGE DIRECTIONS
EXTRACTION FOR
ANISOTROPIC DIFFUSION
WITH PDE
4.1 Estimation of a Gradient and Two
Edge Directions
Steerable filters (Freeman and Adelson, 1991) (Ja-
cob and Unser, 2004) or anisotropic edge detectors
(Perona, 1992) perform well in detecting large lin-
ear structures. Close to corners however, the gradient
magnitude decreases as the edge information under
the scope of the filter decreases. Consequently, the
robustness to noise becomes worse.
A simple solution to bypass this effect is to con-
sider paths crossing each pixel in several directions.
Wedge steerable filters introduced by Simoncelli and
Farid (Simoncelli and Farid, 1996) are composed of
asymmetric masks providing orientation of edges in
different directions from a pixel. Unlike the Gaussian
function, which is an optimal solution for the Canny
criteria (Canny, 1986), wedge steerable filters have
little effect near the center of the mask, whereas points
in the distance are more weighted. The idea devel-
oped in (Montesinos and Magnier, 2010) was to “cut”
the derivative (and smoothing) anisotropic Gaussian
kernel in two parts: a first part along an initial di-
rection, and a second part along a second direction.
At each pixel of coordinates (x,y), a derivation fil-
ter is applied to obtain a derivative information called
Q (x,y,θ):
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
76

Q (x,y,θ) = I
θ
∗C
1
· H (−y) ·x ·e
−(
x
2
2λ
2
+
y
2
2µ
2
)
(2)
where C
1
represents a normalization coefficient.
Thus, Q (x, y,θ) represents the slope of a line derived
from a pixel in the perpendicular direction to θ.
To obtain a gradient k∇Ik and its associated di-
rection η on each pixel P, we first compute global
extrema of the function Q (x, y,θ), with θ
1
and θ
2
. θ
1
and θ
2
define a curve crossing the pixel (an incoming
and outgoing direction). Two of these global extrema
can then be combined to maximize k∇Ik, i.e.:









k∇Ik = max
θ∈[0,360[
Q (x,y, θ) − min
θ∈[0,360[
Q (x,y, θ)
θ
1
= argmax
θ∈[0,360[
(Q (x,y, θ))
θ
2
= argmin
θ∈[0,360[
(Q (x,y, θ))
(3)
Once k∇Ik, θ
1
and θ
2
have been obtained, the
edges can be easily extracted by computing local
maxima of k∇Ik in the direction of the angle η =
(θ
1
+ θ
2
)/2 followed by an hysteresis threshold (see
(Montesinos and Magnier, 2010) for further details).
In this paper, we are solely interested in the two direc-
tions (θ
1
,θ
2
) and the gradient magnitude used in our
diffusion scheme discussed bellow.
Finally, due to their thinness, rotating filters en-
able computing two precise diffusion orientations in
the edge directions, even at high noise levels (Magnier
et al., 2012). In (Magnier et al., 2011a), the authors
have evaluated the edge detection used in this method
with a strong noise level with and without gamma cor-
rection. A comparison with other approaches (De-
riche, 1992) (Perona, 1992) shows the efficiency of
this method.
4.2 Anisotropic Diffusion in Two
Directions of Edges
As diagrammed in Fig 1 (b), the goal here is to diffuse
only in the θ
1
and θ
2
directions in regions of pixels
classified as edge points and isotropic elsewhere. We
will begin by controlling the diffusion as a function of
the gradient magnitude and then as a function of the
angle between the two diffusion directions θ
1
and θ
2
.
Fig. 2 (e) display a diffused image without a control
function wherein edges and small objects are lost and
blurred (20 iterations of diffusion).
In order to control the diffusion through the gra-
dient magnitude, as in (Perona and Malik, 1990) and
(Alvarez et al., 1992), we use the following function
u(k∇Ik) = e
−(k∇Ik/k)
2
, with k ∈ [0,1].
Using the anisotropic perceptual edge detector, we
are now able to control the diffusion as a function
of the angle between θ
1
and θ
2
(see eq. 3) which
0
0.2
0.4
0.6
0.8
1
0
90
180
270
360
0
0.5
1
|¢ I |
`
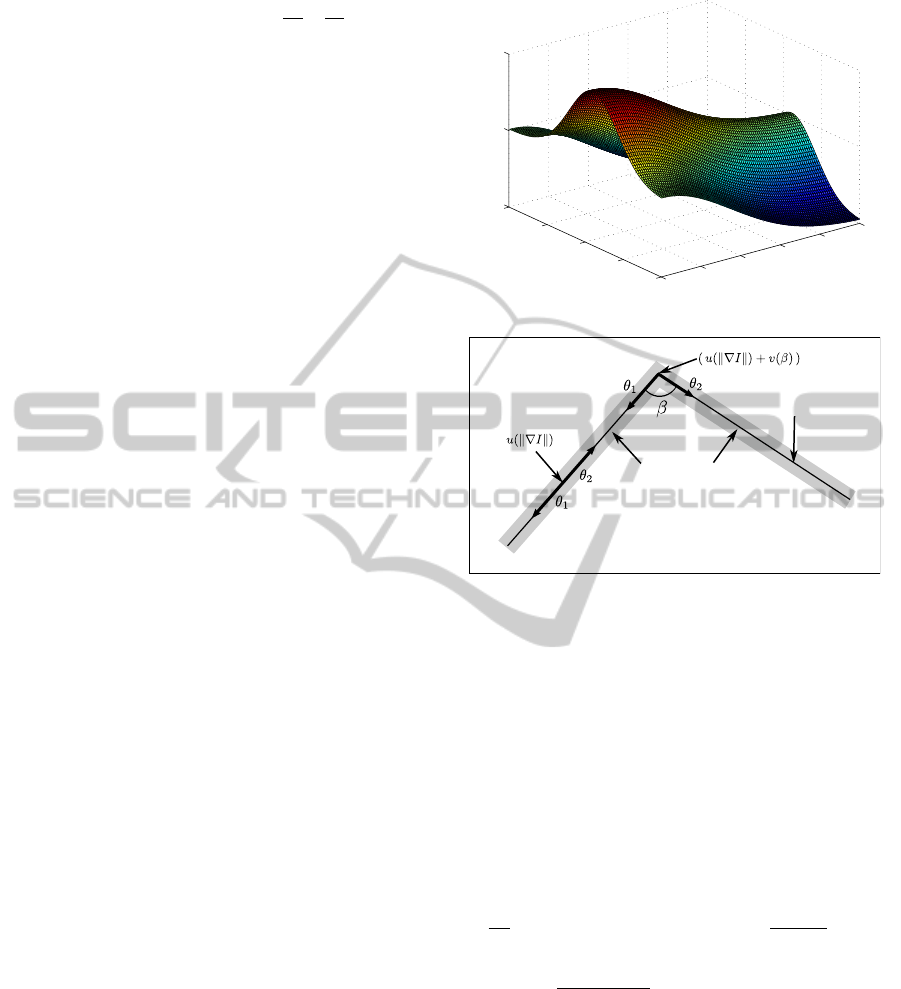
(a) Control function f
c
with k = 0.5 and h = 0.8
(Anisotropic diffusion)
Flat areas detected
Edge
Isotropic diffusion
/
Isotropic diffusion
(b) Diagram of our diffusion.
Figure 1: Control functions (u, v) and diagram of our diffu-
sion scheme.
is labelled β such that β = (θ
1
− θ
2
).. At a pixel
level, the closer β is to 0, the smaller the effect of
diffusion. On the other hand, as β moves closer to
180
◦
, smoothing becomes more pronounced. Thus,
the angular control function, similar to u, is defined
by v = e
−[(180−β)/(180·h)]
2
, with h ∈ [0, 1].
The diffusion process is now described by the fol-
lowing PDE :
∂I
t
∂t
= F
A
(I
0
)∆I
t
+ f
c
· (1 − F
A
(I
0
)) ·
∂
2
I
t
∂θ
1
∂θ
2
(4)
where f
c
=
u(k∇I
0
k)+v(β)
2
represents the control func-
tion for both the gradient magnitude and the angle of
edge orientations, t is the diffusion time, I
0
the origi-
nal image, I
t
the diffused image at time t, (θ
1
,θ
2
) the
two directions of the diffusion and lastly F
A
represents
those regions where flat areas have been detected (see
Section 3): F
A
= 0 in contour regions and F
A
= 1 in
homogeneous regions (Magnier et al., 2011b) (Mag-
nier et al., 2012).
In practice, for MRI images results, the values
k=0.5 and h=0.8 (Fig. 1(a)) enable accurately con-
trolling the diffusion along the edges and corners.
AToolforBrainMagneticResonanceImageSegmentation
77

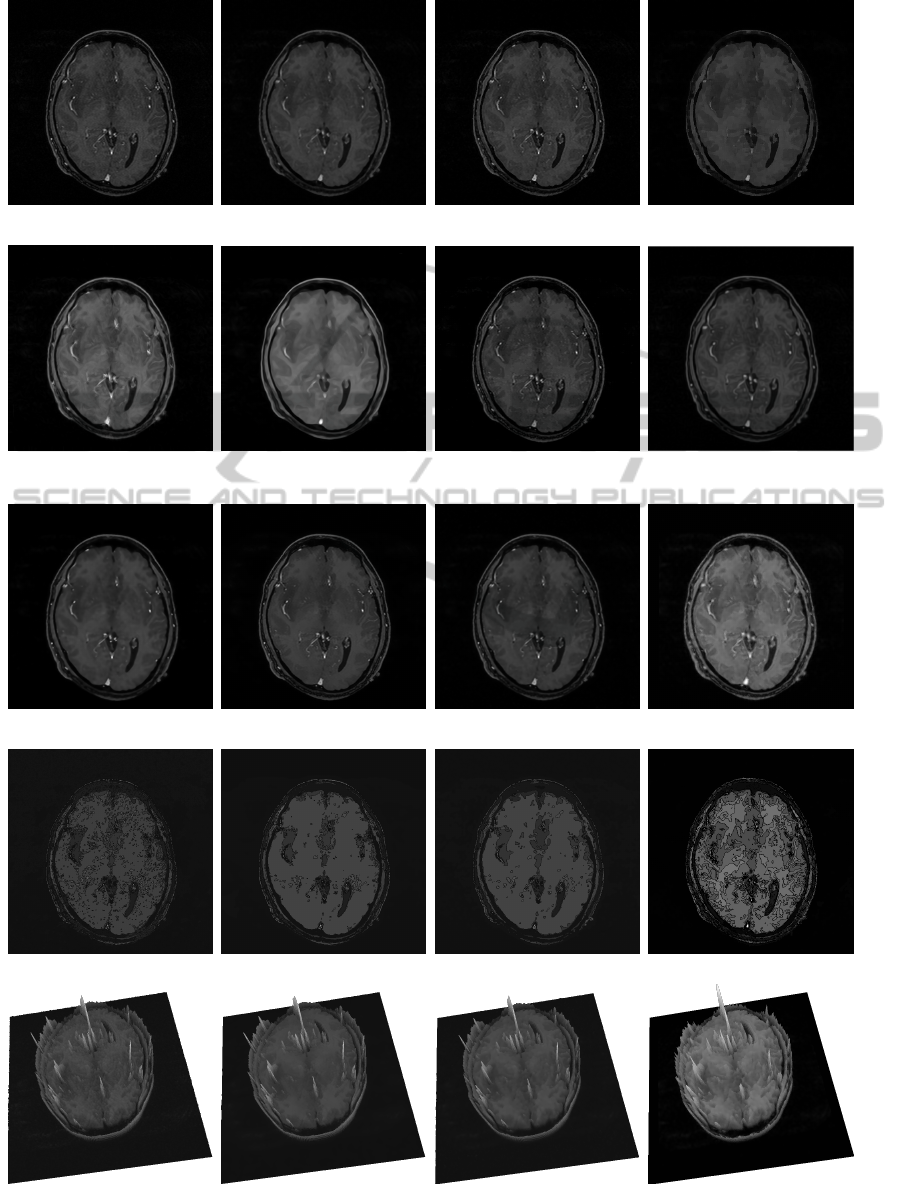
(a) Corrected image
512×512
(b) Median filter
5×5
(c) Nagao filter
(Nagao and Matsuyama, 1979)
(d) Kuwahara filter
(Kuwahara et al., 1976)
(e) Diffusion only in (f) MCM (Catt
´
e et al., 1995) (g) PM (Perona and Malik, 1990) (h) Weickert, (Weickert, 1999),
θ
1
and θ
2
directions. 20 iterations. 100 iterations. σ=1, 50 iterations.
(i) Alvarez et al. (Alvarez et al.,
1992), σ=1, 10 iterations.
(j) Bilateral filter, variance = 5.
(Tomasi and Manduchi, 1998)
(k) Tschumperl
´
e , σ=1, 10 itera-
tions. (Tschumperl
´
e, 2006)
(l) Our result,
20 iterations.
(m) Isohotes of (a) (n) Isohotes of (j) (o) Isohotes of (k) (p) Isohotes of (l)
(q) Surface of (a) (r) Surface of (j) (s) Surface of (k) (t) Surface of (l)
Figure 2: Brain MRI restoration, isophotes and 3D elevation (normalized images).
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
78

5 RESULTS AND CONCLUSIONS
In the image presented in Fig.2(a), the aim is to
smooth the noise present in the images while preserv-
ing both the white and the grey matters. We used
our detector with µ = 5, λ = 1.5 and ∆θ = 5
◦
for re-
gions classification. The threshold for the edge/region
classifier s
th
is equal to 0.002. Parameters used in
anisotropic edge detector in order to compute (θ
1
,θ
2
)
are µ = 5, λ = 1 and ∆θ = 2
◦
. The results of our
anisotropic diffusion are presented in the Fig. 2(l).
Note that the limit between the grey and the white
matter is perfectly visible, Fig. 2(t) illustrates the
sharpness of this edge.
We compare our result with several approaches
as well as the well known median, Nagao (Nagao
and Matsuyama, 1979), Kuwahara (Kuwahara et al.,
1976) and bilateral filters (Tomasi and Manduchi,
1998). For these different methods, the noise is not
completely removed and grey matter edges are not
preserved. Tensorial approaches bring either a fiber
effect to the image (Weickert, 1999) or grey matter is
blurred (Tschumperl
´
e, 2006), as for the approach of
(Alvarez et al., 1992).
In order to show the efficiency of our method for
noise removal and edge of grey/white matter contours
enhancement, we show the image surface of our re-
sults. The 3D elevation of our result allows to see
that grey/white matter edges are well preserved and
sharped. Figs. 2 (m), (n), (o) and (p) show the
isophotes (curves of the image surface of constant in-
tensity) according to 15 levels. It is visible that our
approach preserves also small objects which could be
a tumor or a default inside the brain.
We have proposed in this paper a method for re-
moving noise preserving white/grey matters edges in
MRI images by pixel classification using a rotating
smoothing filter followed by a PDE. Our classifica-
tion method seems very promising as we have been
able to classify correctly white/grey matters edges.
Anisotropic diffusion in two directions provided by
an edge detector using half smoothing kernels keeps
edges and corners of different objects. Comparing our
results with existing algorithms allows us to validate
our method. Next on our agenda is to develop an in-
ternet platform where users could experiment restora-
tion with their own images and apply a segmentation
on the result.
REFERENCES
Alvarez, L., Lions, P.-L., and Morel, J.-M. (1992). Image
selective smoothing and edge detection by nonlinear
diffusion, ii. SIAM J. of Num. Anal., 29(3):845–866.
Aubert, G. and Kornprobst, P. (2006). Mathematical prob-
lems in image processing: partial differential equa-
tions and the calculus of variations (second edition),
volume 147. Springer-Verlag.
Canny, F. (1986). A computational approach to edge detec-
tion. IEEE TPAMI, 8(6):679–698.
Catt
´
e, F., Dibos, F., and Koepfler, G. (1995). A morpholog-
ical scheme for mean curvature motion and applica-
tions to anisotropic diffusion and motion of level sets.
SIAM J. Numer. Anal., 32:1895–1909.
Deriche, R. (1992). Recursively implementing the gaussian
and its derivatives. In ICIP, pages 263–267.
Freeman, W. T. and Adelson, E. H. (1991). The design and
use of steerable filters. IEEE TPAMI, 13:891–906.
Jacob, M. and Unser, M. (2004). Design of steerable filters
for feature detection using canny-like criteria. IEEE
TPAMI, 26(8):1007–1019.
Klauschen, F., Goldman, A., Barra, V., Meyer-Lindenberg,
A., and Lundervold, A. (2009). Evaluation of auto-
mated brain mr image segmentation and volumetry
methods. Human brain mapping, 30(4):1310–1327.
Kuwahara, M., Hachimura, K., Eiho, S., and Kinoshita, M.
(1976). Processing of ri-angiocardiographic images.
Digital Processing of Biomedical Images, pages 187–
203.
Magnier, B., Montesinos, P., and Diep, D. (2011a). Fast
Anisotropic Edge Detection Using Gamma Correction
in Color Images. In IEEE 7th ISPA, pages 212–217.
Magnier, B., Montesinos, P., and Diep, D. (2011b). Texture
Removal in Color Images by Anisotropic Diffusion.
In VISAPP, pages 40–50.
Magnier, B., Montesinos, P., and Diep, D. (2012). A new
region-based pde for perceptual image restoration. In
VISAPP, pages 56–65.
Montesinos, P. and Magnier, B. (2010). A New Perceptual
Edge Detector in Color Images. In ACIVS, volume 2,
pages 209–220.
Nagao, M. and Matsuyama, T. (1979). Edge preserving
smoothing. CGIP, 9:394–407.
Perona, P. (1992). Steerable-scalable kernels for edge detec-
tion and junction analysis. IMAVIS, 10(10):663–672.
Perona, P. and Malik, J. (1990). Scale-space and edge
detection using anisotropic diffusion. IEEE TPAMI,
12:629–639.
Poynton, C. (1996). A technical introduction to digital
video. John Wiley & Sons, Inc. New York, NY, USA.
Simoncelli, E. and Farid, H. (1996). Steerable wedge filters
for local orientation analysis. IEEE TIP, 5(9):1377–
1382.
Tomasi, C. and Manduchi, R. (1998). Bilateral filtering for
gray and color images. In International Conference
on Computer Vision, pages 839–846. IEEE.
Tschumperl
´
e, D. (2006). Fast anisotropic smoothing
of multi-valued images using curvature-preserving
PDE’s. IJCV, 68(1):65–82.
Weickert, J. (1999). Coherence-enhancing diffusion filter-
ing. IJCV, 31(2):111–127.
AToolforBrainMagneticResonanceImageSegmentation
79