Cargo Transportation Models Analysis using Multi-Agent Adaptive

Real-Time Truck Scheduling System

Oleg Granichin

, Petr Skobelev

, Alexander Lada

, Igor Mayorov

and Alexander Tsarev

Saint Petersburg State University, Saint Petersburg, Russia

Smart Solutions, Ltd, Samara, Russia

Keywords: Multi-agent Systems, Adaptive Scheduling, Trucks, Cargo Transportation, Simulation, Real-Time, Mobile

Resources.

Abstract: The use of multi-agent platform for real-time adaptive scheduling of trucks is considered. The schedule in

such system is formed dynamically by balancing the interests of orders and resource agents. The system

doesn’t stop or restart to rebuild the plan of mobile resources in response to upcoming events but finds out

conflicts and adaptively re-schedule demand-resource links in plans when required. Different organizational

models of cargo transportation for truck companies having own fleet are analyzed based on simulation of

statistically representative flows of orders. Models include the rigid ones, where trucks return back to their

garage after each trip, and more flexible, where trucks wait for new orders at the unloading positions, where

trucks can be late but pay a penalty for this, and finally where orders can be adaptively rescheduled ’on the

fly‘ in real-time and the schedule of each truck can change individually during orders execution. Results of

simulations of trucks profit depending on time period are presented for each model. These results show

measurable benefits of using the multi-agent systems with real-time decision making - up to 40-60%

comparing with rigid models. The profit dependencies on the number of trucks are also built and analyzed.

The results show that using adaptive scheduling in real time it is possible to execute the same number of

orders with less trucks (up to 20%).

1 INTRODUCTION

The problem of resource allocation, scheduling and

optimization are usually solved taking well defined

initial conditions, when all the orders and resources

are given in advance and don’t change in the process

of scheduling. In these cases classical batch planning

methods and tools can be used characterized by the

time-consuming full or constrained combinatorial

search or different types of heuristics still requiring a

lot of computational power (Leung, 2004).

For solving complex problems of real time

resource allocation, scheduling, optimization and

controlling we apply multi-agent technology

(Bonabeau, 2000, Wooldridge, 2002) allowing us to

find acceptable solutions of problem by using

adaptive scheduling of resources.

The adaptive scheduling approach we are

working on is based on Demand-and-Resource

Networks (DRN) of agents representing orders and

resources (Vittikh, 2003, Skobelev, 2010). Agents

can have conflicting interests, an ability to react to

incoming events notifying about changes in orders

and resources, find out conflicts in the schedule,

make decisions and interact with each other in a way

to resolve the conflicts and find trade-offs by

negotiations. That allows us to find a ’well-

balanced‘ solution acceptable for all the agents as

well as for company as a whole.

Despite of the simplicity of the basic classes of

agents and the logic of their competition and

cooperation, which are described in more details in

(Skobelev, 2011), the developed multi-agent

technology allows us to solve complex resource

allocation, scheduling and optimization problems in

real time when the number of orders and resources is

not given in advance and there is a high dynamics of

occurring events (Basra, 2005, Himoff, 2006,

Skobelev, 2010).

One of such problems is the cargo transportation

scheduling in real time, when the time required for

decision strongly affects efficiency of the

transportation. In this paper we show that real-time

decision making and adaptive scheduling provide

significant advantages for cargo transportation.

244

Granichin O., Skobelev P., Lada A., Mayorov I. and Tsarev A..

Cargo Transportation Models Analysis using Multi-Agent Adaptive Real-Time Truck Scheduling System.

DOI: 10.5220/0004225502440249

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 244-249

ISBN: 978-989-8565-39-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

The results of the research are important for the

future developments of intelligent freight

management systems and dispatching of any other

mobile resources that are equipped with GPS

sensors, have online connection with drivers via

mobile phones and are able to operate in real time.

2 THE PROBLEM DEFINITION

Let’s assume that we have a fleet of M trucks based

in certain cities in a transportation network. The

operation cost of each truck is given. Orders come

into the system with the specified points of loading,

points of unloading, loading start time, unloading

finish time, order price and penalties for delays

when a loading or unloading is done later than they

should. Distances between points are also given and

described by a matrix of distances.

The objective is to schedule the trucks in real

time and determine transportation company profit

depending on the scheduling strategy (model) and

the number of trucks. Real-time scheduling means

that at each particular moment only such orders are

considered that have come before this moment. The

optimization criterion of the task is the maximal

total profit of all the trucks in company fleet.

The research is done for four different models of

organization of transportation process including not-

adaptive and adaptive models described below.

3 THE MODELS OF

TRANSPORTATION PROCESS

ORGANIZATION

The total profit of the fleet of trucks is calculated as

a sum of profits of each truck:





P .

(1)

The profit of one truck is:















(2)

where sum includes all orders j executed by the

truck i, c

- price of order j per time unit, q

– cost of

the truck per time unit, t

- time of execution order j

by truck i, t’

– empty run time for order j.

Below we consider four different models

(strategies) of cargo transportation:

1) The ’Returning to base after an order

execution’;

2) The ’No return to base after an order

execution’;

3) The ’Delays with penalties’;

4) The ’Adaptive scheduling with penalties’.

Model 1 – The ’Returning to base after an order

execution’ model. After each order execution the

truck should return to the base point. Order is

assigned to a truck that has a “window” in its

schedule during the order time period. If the loading

point of the order is a different city, then the truck

should arrive there at the loading time. No

reassignments of the trucks already assigned to the

orders are allowed.

Model 2 – The ’No return to base after an order

execution‘ model. After each order execution truck

stays at the order destination point, without returning

to base, and waits for a next order.

Model 3 – The ’Delays with penalties‘ model.

Orders can be scheduled with delays of time of

arrival at the loading point.

In this case profit with penalty calculation is:















'''







(3)

where the sum by index j includes all orders that

were executed just in time by the truck i, the sum by

index k includes all orders that were executed with

delays t

’’

, p

– penalty of each delay per time unit.

Model 4 – The ’Adaptive scheduling with

penalties‘ model. It is equal to the previous model,

but it allows the truck reassignment when a profit

from a new order is higher than a profit from the

previous one. So then a new order comes, the

reassignment starts and it reorganizes part of orders

that are already assigned to resources, in order to

find a more profitable solution.

4 OVERVIEW OF THE

MULTI-AGENT SIMULATOR

OF REAL-TIME SCHEDULING

SYSTEM FOR CARGO

TRANSPORTATION

A special multi-agent simulator (MAS) has been

created for modeling of adaptive real time

scheduling. This system provides functionality for

simulation and experimenting with the flows of

modeled orders, randomly generated or manually

constructed. It works as follows. Every truck is

associated with a truck agent, every order – with an

order agent. The agents are able to send and receive

messages in MAS-environment and take decisions

according to their logic and current situation, which

CargoTransportationModelsAnalysisusingMulti-AgentAdaptiveReal-TimeTruckSchedulingSystem

245

is de-fined by state of every agent. The unified

spatio-temporal scale is defined to achieve visibility

of results and unified logic: time is counted from the

start of the modeling process, i.e. from the moment

of the first order entry. The upper border of planning

is determined by the planning horizon, calculated in

days. The distances are brought to time scale by

division of the distances by the average speed. By

doing this, we can account for quality conditions and

traffic capacity of roads (that’s why longer road can

result in shorter trip due to higher speed, it allows).

Current states of agents are changing and are

measured when new orders come into the system

and at the moments of start and finish of execution

of each order. That’s why the scale of N orders in

general case consists of 3N points.

When a new order comes into the MAS-system,

a request for its allocation is sent to all the truck

agents. Then the agents analyze their current state,

availability of ’time slots‘ in the future schedule,

need for empty run to loading point, assess their pos-

sible profit and send answer to the order agent.

’Candidates‘ for re-scheduling (in case of increasing

profit) are ordered of the prospective profit. Then the

order agent chooses the truck that gives the maximal

profit. The profit is calculated as a difference

between the order revenue (price) and the order full

cost. When order implies an empty run to loading

point, its cost is also deducted from the revenue.

That’s why orders with high revenue, but long

empty runs to loading points, can be ousted by

orders with lower revenue, but without empty runs.

In case of strategy (model), where penalties are

applied, their influence on profit is analyzed. For

penalty is proportional to time of delay, the orders

with big delays will not be scheduled. Orders in the

past (earlier than the current time) do not participate

in the scheduling.

The process continues by processing of the

events of order arrival, start and finish of order

execution, simulating real-time order management.

In the process of research the above 4 models of

cargo transportation were implemented and

compared to show benefits of adaptive scheduling.

5 WORLD OF SIMULATIONS

Let’s consider world of simulations and example of

calculation of fleet profit in adaptive real time

scheduling for one truck. Let’s look at the example.

There are 4 cities (points) given, among which

the distances are determined by the matrix (see

Table 1) in days of trip. Time of trip doesn’t

necessarily correspond to the distance, because

quality of roads may be different that affects the

maximum speed of truck on the roads.

Table 1: Matrix of distances among cities.

Point 1 Point 2 Point 3 Point 4

Point 1 0 1 1 2

Point 2 1 0 2 1

Point 3 1 2 0 1

Point 4 2 1 1 0

Table 2: Parameters of orders.

Characteristics

Order number

1 2 3 4 5

Time of entry

1 3 5 6 7

Start time of execution

3 4 7 8 9

Finish time of execution

5 5 9 9 10

Where from

4 3 1 4 3

Where to

1 1 4 3 1

At the beginning of the trip the truck is located in

the point 1.

At different times cargo transportation orders #1-

5 to different points come into the system. Duration

of execution of an order is 1-2 days. Scheduling

horizon equals t = 10 days. The costs of orders are

calculated equally using company tariff as c = 3

standard units (SU) / day, i.e. 2-days trip would have

cost of 6 SU. Idle time of a truck leads to daily loss

of qa=0.3 SU. Use 15-point type for the title, aligned

to the center, linespace exactly at 17-point with a

bold font style and all letters capitalized. No

formulas or special characters of any form or

language are allowed in the title.

Daily running cost in case of empty run of truck

or order execution is q=1. Drivers are allowed to

execute orders with delays, but every day of delay

costs pp = 0.6 SU. Some orders are shifted to the

right on the time axis because of this. The aim is to

be able to schedule trips, as orders come in (the

orders are not known in advance) and calculate

profit.

Orders are marked with a number according to

the place in the sequence of entry into the system

and characterized by time of their entry (moment of

entry t), moments of start and finish of order

execution, duration (in days), point of loading and

point of unloading (Table 2).

Figure 1 shows orders as rectangles, with the

order number and the time of entry, divided by

comma inside the rectangle, above each rectangle

’where from – where to‘ locations are described. The

start and the finish of each rectangle correspond to

the start and the finish of the order execution.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

246

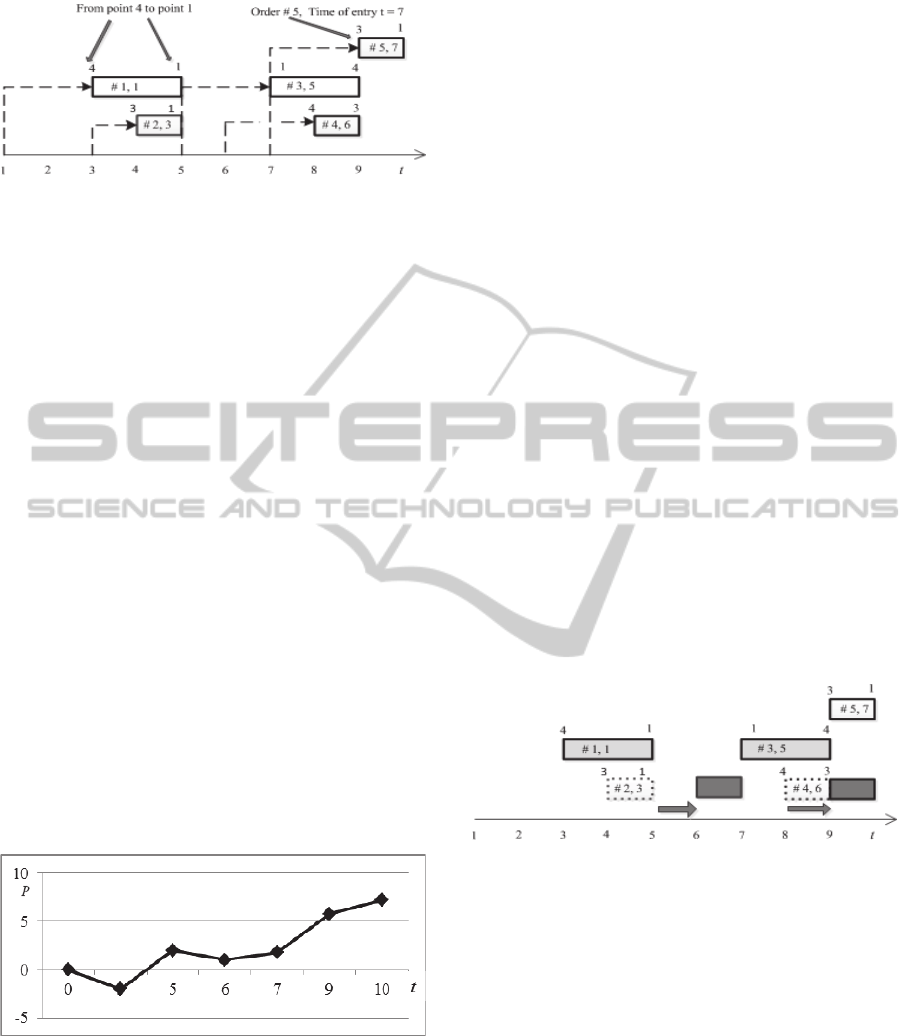
Figure 1: Diagram of orders entry and scheduling.

Let’s calculate the profit of truck# 1 in the Model

#3, where penalties are applied. We will calculate

the profit v at the moments of transition of the truck

from one state to another. Let’s look at the step by

step profit calculation.

Execution of order #1 will require to start at the

moment t=1 from point #1 to point # 4 and will take

2 days till the moment t=3. At the moment t=3 the

profit is P=-q*2=-2. Let’s show the change of the

profit P in real time (Figure 2).

The transportation of cargo from point 4 to the

point 1 will take 2 days, and at t=5 the truck will

arrive at the point 1 with the profit p=-2+(c-q)*2=-

2+2*2=2.

Assume that the truck agent assesses options of

further schedule and execution upon arrival to point

1 at time t=5. Its profit at point 4 is v=2. By this time

order # 3 has been entered at the moment of time #3.

There are two options to execute it:

 Order #2 is to be executed with delay;

 Order #2 is rejected, idle time cost is

accepted, order #3 from the same point 1 is to be

taken; for order # 2 can be executed with delay

before execution of order #3, no further options

will be taken into consideration. Let’s take a

more precise look at 2 options.



Figure 2: Profit of truck agent depending on time.

Truck needs to reach point 3, moving from point

1 (1 day trip), pick up the order and execute it, going

from point 3 to point 1 (1 day). The increase of

profit is dp=-1*q+(c-q)*1=-1+2=1.

Penalty applied because of delay is -pp*2=-

2*0.6=-1.2. As a result the truck will be at the

moment t=7 at the point 1 with the profit P=2+1-

1.2=1.8. Execution of the order would seem to be

unprofitable, but one should take into consideration

that in case of cancellation of the order the truck

would stay idle for 2 days, and the profit at the

moment t=7 would be P=2-2*0.3=1.4.

That’s why the truck agent is interested in the

execution of order #2 with delay, order #3, t= 7…9

(from point 1 to point 4) - 2 days, profit is

P=1.8+2*(c-q)=1.8+2*2=5.8, and the truck moves to

point 4.

At the moment t=9 new order# 5 comes in at the

point 3 with start time of execution t=9; empty run

to its loading point is 1 day, what puts the order

beyond the 10-days scheduling horizon limit. That’s

why the truck agent rejects the order. There is an

outdated order #4 from point 4 to point 3, its

execution start time should be t=8. The truck agent

assesses profit from possible shift of order by a day.

Execution of the order #4, empty run is not

required, dp=(3-1)*1=2-penalty 0.6=1.4. If this

order were rejected, the truck would stay idle for 1

day till the end of the scheduling horizon and then

dp=-1*0.3=-0.3.. That’s why the truck agent accepts

the order #4.

Outcome: orders #1 and 3 are executed without

delay, order #2 – with allowed delay of 2 days and

order #4 – with allowed delay of 1 day. Order #5 is

rejected (Figure 3).

Total profit in 10 days is P=5.8+1.4=7.2.

Figure 3: Diagram of execution of adaptive schedule by

one truck.

The delayed orders on Figure 3 are shown with

dark grey, when penalties are applied; light grey

marks orders without delay; shifts in schedule are

shown with wide arrows; shifted orders are shown

with dotted borders; rejected order is white (not

visible). White arrows stand for empty runs, light

grey ones – executions of orders with delay; dark

grey ones – executions of orders on time.

As a larger-scale example, task of scheduling of

execution of 100 orders for 10 trucks has been

studied (Figure 4). The Figure 4 shows incoming

orders, where the length of a segment shows a

preferred time of the order execution.

CargoTransportationModelsAnalysisusingMulti-AgentAdaptiveReal-TimeTruckSchedulingSystem

247

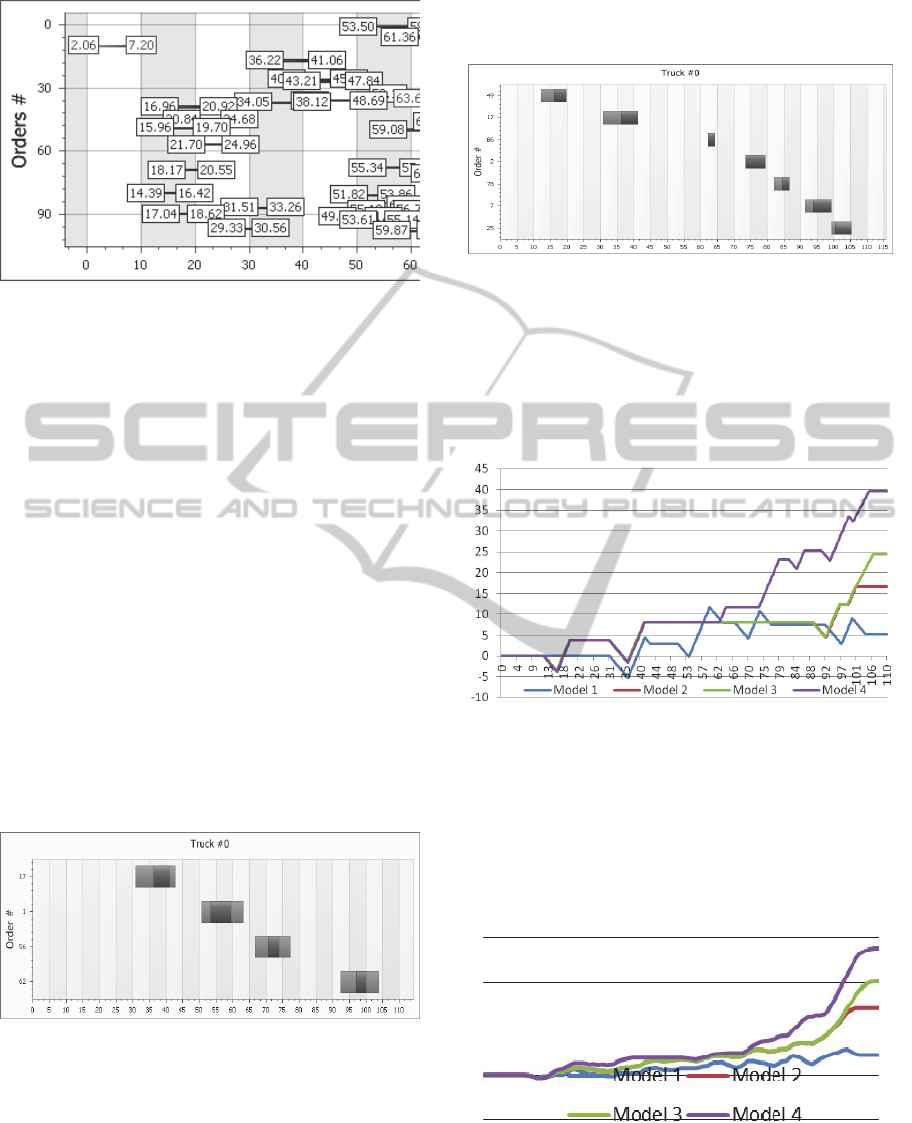
Figure 4: Allocation of input orders in time.

Orders were generated with equal distribution

among cities (points) and by dates. Times of start of

execution are also equally distributed, but all –

within the time of entry and the end of the

scheduling horizon. That’s why the intensity of

orders increases at the end of the time period of

simulation. Trucks are based initially in one point –

base. Orders are distributed equally among 18

points. Distances between points are from 1 to 6.

The scheduling horizon is 100 days.

6 THE RESULTS OF THE

EXPERIMENTS

Trucks schedules were created for orders based on

the 4 used models of transportation. As an example

of the result let’s see the schedule (Gantt chart) of

truck #0 in the Model 1 and Model 4 which are

presented on Figure 5 and Figure 6.

Figure 5: Truck schedule in the Model 1 with returning to

base.

Horizontal axis of Figure 5 and Figure 6 shows

time in days, vertical shows orders numbers. The

executed orders are shown in a dark colour. Brighter

rectangles before an order accord to a trucks running

process in a loading point. Rectangles on the Figure

5 also show a truck that is returning to base point

according the Model 1. Dark rectangle on Figure 6

shows an order that was executed with delay and

penalty.

Figure 6: Truck schedule in the Model 4 with adaptive

reschedule and penalties.

Graphs of dynamic profit per each truck

depending on time was found. Figure 7 shows profit

dynamics for the truck according to Model 1 –Model

4. It accords the truck schedules represented above

by the Gantt chart diagrams.

Figure 7: Dynamics of a profit for the truck depending on

model of transportation.

Straight horizontal segments accord to a truck

stop periods, segments with positive growth show a

profit growth while an order was running, segments

with negative growth show idle run costs of the

truck to the loading point or to the base in the Model

Figure 8: Dynamics of sum of trucks profit depending on

transportation models.

The summary profit for all vehicles in each of

the 4 models of transport is the sum of profits in

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

248

each truck. It’s shown in Figure 8.

The designed MAS allows also to study the

profit depending on trucks number for each flow of

orders. For simplicity we don’t consider standing

costs of trucks. For the initial orders schedule

(Figure 4) the trucks schedules and approximate

profit were modeled according to Model 1 – Model

The trucks amount was varied from 0 to 50

(Figure 9).

Figure 9: The dependence of the profit to the used trucks

number in the different transportation models.

Each graph of total profit has two typical

regions. The first region contains an almost linear

increase profits with the number of trucks and the

second is a ’saturation’ region, for which the profit

is almost constant and does not vary with the

number of trucks. That is due to the fact that most of

the new orders have been assigned to the trucks.

Saturation modes differ for the different models.

The lowest profit value is in the Model 1 because

less amount of orders are scheduled and additional

expenses occur after returning to the base. The

Model 3 far exceeds the Model 2 because it uses the

same amount of trucks as in the Model 2 but more

orders are scheduled. But in a satiation mode it gives

almost no benefits vs. the Model 2, because when

the trucks number is high enough there are very few

orders that are executed with delays so The Model 2

and the Model 3 will be almost equal.

The Model 4 is the best one. It gives approximate

20% more profit then the Model 2 and the Model 3.

It allows using less trucks during the plan execution.

The reason is the adaptive re-scheduling of

orders in real time.

7 CONCLUSIONS

The paper studies benefits of multi-agent system for

real time adaptive truck allocation, scheduling and

optimization in long-distance transportations of

cargos.

It was shown that multi-agent technology allows

to create significantly more profitable schedules (up

to 40-60% compared with rigid models) and save a

number of trucks (up to 20%) for the same amount

of orders. The results of the research can be used for

improving management of any type of mobile

resources.

REFERENCES

Leung , Y-T., 2004. Handbook of Scheduling: Algorithms,

Models and Performance Analysis. Chapman & Hall.

London.

Bonabeau, E., Theraulaz, G., 2000. Swarm Smarts. What

computers are learning from them? Scientific

American, vol. 282, no. 3, pp. 54-61.

Wooldridge, M., 2002. An Introduction to Multi-Agent

Systems. JohnWiley & Sons. London, 2

edition.

Vittikh, V., Skobelev, P., 2003. Multi-Agent Models for

Designing Demand-and-Resource Networks in Open

Systems. Automation and Remote Control, vol. 64, no.

1, pp. 162-169.

Skobelev, P., 2010. Bio-Inspired Multi-Agent Technology

for Industrial Applications. Multi-Agent Systems –

Modeling, Control, Programming, Simulations and

Applications. Faisal Alkhateeb, Eslam Al Maghayreh

and Iyad Abu Doush (Ed.). InTech Publishers. Austria.

28 p.

Skobelev, P., 2011. Multi-agent technology for real time

resource allocation, scheduling, optimization and

controlling in industrial applications. In HoloMAS

2011, 5th International Confrence on Industrial

Applications of Holonic and Multi-Agent Systems.

Springer. Berlin. pp. 1-14.

Basra, R., Lü, K., Rzevski, G., Skobelev, P., 2005.

Resolving Scheduling Issues of the London

Underground Using a Multi-Agent System. In Lecture

Notes in Artificial Intelligence (Subseries of Lecture

Notes in Computer Science), 3593. pp. 188-196.

Himoff, J., Rzevski, G., Skobelev, P., 2006. Magenta

Technology: Multi-Agent Logistics i-Scheduler for

Road Transportation. In AAMAS 2006, 5th

International Conference on Autonomous Agents and

Multi Agent Systems. Japan.

Skobelev, P., 2010. Multi-Agent Technologies for

Industrial Applications: Towards 20 years Anniversary

of Samara Scientific School of Multi-Agent Systems.

Mechatronics, Automation, Control, no. 12, pp. 33-

46.

CargoTransportationModelsAnalysisusingMulti-AgentAdaptiveReal-TimeTruckSchedulingSystem

249