
Evaluation of a Self-organizing Heuristic for Interdependent Distributed
Search Spaces
Christian Hinrichs
1
, Michael Sonnenschein
1
and Sebastian Lehnhoff
2
1
Department for Environmental Informatics, University of Oldenburg, Oldenburg, Germany
2
R&D Division Energy, OFFIS Institute for Information Technology, Oldenburg, Germany
Keywords:
Self-organization, Cooperation, Combinatorial Optimization, Smart Grid.
Abstract:
Whenever multiple stakeholders try to optimize a common objective function in a distributed way, an adroit
coordination mechanism is necessary. This contribution presents a formal model of distributed combinato-
rial optimization problems. Subsequently, a heuristic is introduced, that uses self-organizing mechanisms to
optimize a common global objective as well as individual local objectives in a fully decentralized manner.
This heuristic, COHDA
2
, is implemented in an asynchronous multi-agent system, and is being extensively
evaluated by means of a real-world problem from the smart grid domain. We give insight into the conver-
gence process and show the robustness of COHDA
2
against unsteady communication networks. We show that
COHDA
2
is a very efficient decentralized heuristic that is able to tackle a distributed combinatorial optimiza-
tion problem with regard to multiple local objective functions, as well as a common global objective function,
without being dependent on centrally gathered knowledge.
1 INTRODUCTION
By exploiting the limitations and constraints that are
inherent to the search space of valid solutions, many
real-world optimization problems can be solved very
efficiently. Such approaches, however, are based on
global knowledge and can not be directly transferred
to decentralized systems, where the search space is
distributed into disjoint subspaces. One possible ap-
proach might be to communicate the locally available
information to a central place. However, this is not al-
ways desirable. For example, the global collection of
data might violate privacy considerations. The gather-
ing of such data might even be impossible, as it is the
case if local search spaces are partially unknown or
cannot be enumerated (i.e. due to infiniteness). An-
other limitation is that distributed search spaces are
often not independent. Such interdependencies re-
quire to evaluate search spaces with relation to each
other. Thus, a parallel search for optimal solutions
would require a large communication overhead.
For instance, this type of problem is present in the
smart grid domain. According to (Gellings, 2009),
”a smart grid is the use of sensors, communications,
computational ability and control in some form to en-
hance the overall functionality of the electric power
delivery system.” We focus on active power schedul-
ing, which can be expressed as a combinatorial op-
timization problem. Here, a collective power profile
is to be produced by a number of devices, which can
then be sold as a product on a market, for example.
However, individual constraints of the devices have
to be considered, which may be known only to the
concerning device. Due to temporal overlaps between
device schedules, the quality of an individual sched-
ule (with respect to the global goal of realizing the
given power profile) usually depends on the current
schedule selection of several other devices. These in-
terdependencies can only be tackled through commu-
nication between devices during the search process.
For this purpose, a swarm-based method is devel-
oped which makes use of self-organization strategies.
In hitherto existing population-based heuristics, each
individual represents a solution to the given problem
within a common search space. In our approach, how-
ever, an individual incorporates a local, dependent
search space, and thus defines a partial solution that
can only be evaluated with respect to all other indi-
viduals. The task of each individual is to find a partial
local solution that, if combined with all other local
solutions, leads to the optimal global solution.
The contribution is organized as follows. In sec-
tion 2, the MC-COP problem is recalled from liter-
ature and subsequently is extended to a distributed
25
Hinrichs C., Sonnenschein M. and Lehnhoff S..
Evaluation of a Self-organizing Heuristic for Interdependent Distributed Search Spaces.
DOI: 10.5220/0004227000250034
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 25-34
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

variant with multiple objectives. A self-organizing
heuristic for this problem, COHDA
2
, is introduced
in section 3. Following, Section 4 gives an extensive
evaluation of the heuristic. Section 5 relates the ap-
proach to existing work. The contribution concludes
with a summary and an outlook in Section 6.
2 PROBLEM DEFINITION &
MODEL
As a first approach, we restrict our point of view
to combinatorial optimization problems (COP). Such
problems can easily be modelled if we assume that
each search space is discrete by nature, and that
the elements within are known and may be enumer-
ated. From a central perspective, these problems may
be formulated with an integer programming model.
In (Hinrichs et al., 2012), the multiple-choice com-
binatorial optimization problem (MC-COP) is de-
scribed as:
min
c −
m
∑
i=1
n
i
∑
j=1
(w
i j
· x
i j
)
1
(1)
subject to
n
i
∑
j=1
x
i j
= 1, i = 1 . . . m,
x
i j
∈ {0, 1}, i = 1. . . m, j = 1 . . . n
i
,
Here, m search spaces are defined with each search
space s
i
containing n
i
partial solutions. The jth partial
solution in search space s
i
is described by an element
j with a value w
i j
. Note that this value may be a vec-
tor and thus may have any number of dimensions. The
goal is to select a value w
i j
from each search space s
i
,
so that the sum of these selected values approaches a
given target c as close as possible. This is a general-
ization of the well-known subset-sum problem, which
does not allow solutions > c. Since from each search
space exactly one element (no more, no less) has to
be chosen for a feasible global solution, each element
w
i j
∈ s
i
in this model has an associated selection vari-
able x
i j
, wich defines whether an element has been
chosen (x
i j
= 1) or not (x
i j
= 0).
2.1 Distributed-objective Model
In the contribution at hand, we would like to extend
the centrally driven MC-COP (1) to the distributed
case. In our approach, each local search space s
i
is
represented by a single agent a
i
, whose task is to se-
lect one of its elements w
i j
with respect to a common
global goal c. More formally, an agent a
i
has to find
an assignment of its own selection variables x
i j
, such
that the objective function in (1) is minimized.
Definition 1. A selection of an agent a
i
is a tu-
ple γ
i
= hi, ji where i is the identifier of a
i
and j
identifies the selected element w
i j
such that x
i j
= 1,
∑
n
i
j=1
x
i j
= 1.
In order to decide which of its local elements
w
i j
∈ s
i
yields the optimum, an agent has to take the
selections of the other agents in the system into ac-
count.
Definition 2. A context is a set Γ = {γ
i
, γ
k
, . . . } of
selections. A selection belonging to an agent a
i
can
appear in a context no more than once:
γ
i
= hi, j
1
i ∈ Γ ∧ γ
k
= hk, j
2
i ∈ Γ ⇒ i 6= k
Note that this definition allows a context to be in-
complete with regard to the population of agents in
the system, which enables us to model a local view,
that an agent a
i
has on the system. This is quite simi-
lar to the definition of context in (Modi et al., 2005).
Definition 3. A global context regarding the whole
system is denoted by Γ
global
= {γ
i
| i = 1 . . . m}.
Definition 4. A perceived context of an agent a
i
is a
context Γ
i
= {γ
k
| a
i
is aware of a
k
}.
Assuming that an agent a
i
is able to somehow per-
ceive a context Γ
i
containing information about other
agents that a
i
is aware of (we will address this in the
following section), it may now select one of its own
elements w
i j
∈ s
i
with respect to the currently chosen
elements of other agents in Γ
i
and the optimization
goal c.
Furthermore, we introduce local constraints,
which impose a penalty value p
i j
(i.e. cost) to each
element w
i j
within the search space s
i
of an agent a
i
.
These local constraints are known to the correspond-
ing agent only, as described in the introductory exam-
ple. Thus, each agent has two objectives: minimizing
the common objective function as given in (1), and
minimizing its local penalties that are induced by con-
tributing a certain element w
i j
. This compound opti-
mization goal at agent level may be expressed with a
utility function:
z
i
= α
i
· z
1
i
+ (1 − α
i
) · z
2
i
(2)
Here, z
1
i
represents the common global objective
function and z
2
i
incorporates the local constraints. The
parameter α
i
allows to adjust the importance of the
global goal versus local constraints of an agent a
i
, and
hence defines the degree of altruism at agent level.
From a global point of view, this yields the
distributed-objective multiple-choice combinatorial
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
26

optimization problem (DO-MC-COP):
min
m
∑
i=1
z
i
(3)
where z
i
= α
i
· z
1
i
+ (1 − α
i
) · z
2
i
,
z
1
i
=
c −
n
i
∑
j=1
(w
i j
· x
i j
) +
∑
w∈Γ
i
w
1
,
z
2
i
=
n
i
∑
j=1
(p
i j
· x
i j
),
subject to
n
i
∑
j=1
x
i j
= 1, i = 1 . . . m,
x
i j
∈ {0, 1}, i = 1. . . m, j = 1 . . . n
i
,
α
i
∈ R, 0 ≤ α
i
≤ 1, i = 1 . . . m .
Summarizing, in this model there are m decision mak-
ers (agents) a
i
, that pursue a common goal by each
contributing one solution element w
i j
from their as-
sociated local search space s
i
, while at the same time
minimizing the resulting local penalties p
i j
. For that,
an agent a
i
evaluates its local search space with re-
spect to the global target c as well as the perceived
context Γ
i
.
Obviously, a change in the selection γ
i
made by
an agent a
i
changes the current global context Γ
global
,
as well as every perceived context Γ
k
which con-
tains γ
i
. Thus, the definition of how an agent a
k
per-
ceives a context Γ
k
, and how this relates to Γ
global
,
is crucial for solving the DO-MC-COP. The follow-
ing section addresses these questions and describes a
self-organizing approach to this distributed-objective
problem.
3 SELF-ORGANIZING
HEURISTIC
In nature, we find many examples of highly efficient
systems, which perform tasks in a completely de-
centralized manner: swarming behavior of school-
ing fish or flocking birds (Reynolds, 1987), foraging
of ants (H
¨
olldobler and Wilson, 1990) and nest ther-
moregulation of bees (Jones et al., 2004). Even pro-
cesses within single organisms show such astonish-
ing behavior, for instance the neurological develop-
ment of the fruit fly (Kroeker, 2011) or the foraging of
Physarum polycephalum, a single-celled slime mold
(Tero et al., 2010), which both exhibit rules for adap-
tive network design. One of the core concepts in these
examples is self-organization. From the perspective
of multi-agent systems, this term can be defined as
”the mechanism or the process enabling a system to
change its organization without explicit external com-
mand during its execution time” (Serugendo et al.,
2005). If such a process executes without any cen-
tral control (i.e. neither external nor internal), it is
called strong self-organization. From the perspective
of complex systems theory, this is related to emer-
gence, which can be defined as ”properties of a sys-
tem that are not present at the lower level [...], but are
a product of the interactions of elements” (Gershen-
son, 2007).
The COHDA heuristic, as proposed in (Hinrichs
et al., 2012), applies these concepts to create a self-
organizing heuristic for solving distributed combi-
natorial optimization problems. Note that we devi-
ate from the formal identifiers used in the referenced
work, to reflect the extended problem description (3).
Moreover, we include local objectives of agents into
the search process, which yields an extended heuristic
COHDA
2
. In the following, we will first extend the
definitions introduced in the previous section to meet
the needs of a heuristic, and subsequently summarize
the process in three steps.
In the considered heuristic, agents iteratively
search for partial solutions. This yields an evolving
process, hence we need to extend the notion of selec-
tion and context (definitions 1 to 4) with a temporal
component, and thus define state and configuration:
Definition 5. The state of an agent a
i
is given by
σ
i
= hγ
i
, λ
i
i, where γ
i
is a selection containing an as-
signment of a
i
’s decision variables x
i j
, and λ
i
is a
unique number within the history of a
i
’s states. Each
time an agent a
i
changes its current selection γ
i
to
´
γ
i
, the agent enters a new state
´
σ
i
= h
´
γ
i
,
´
λ
i
i where
´
λ
i
= λ
i
+ 1. This imposes a strict total order on a
i
’s
selections, hence λ
i
reflects the ”age” of a selection.
Definition 6. A configuration Σ = {σ
i
, σ
k
, . . . } is a
set of states. A state belonging to an agent a
i
can
appear in a context no more than once:
σ
i
∈ Σ ∧ σ
k
∈ Σ ⇒ i 6= k
Definition 7. A global configuration regarding the
whole system is denoted by Σ
global
= {σ
i
| i = 1. . . m}.
Definition 8. A perceived configuration of an agent
a
i
is a configuration Σ
i
= {σ
k
| a
i
is aware of a
k
}.
In the DO-MC-COP model (3), an agent a
i
cre-
ates an assignment of its decision variables x
i j
based
on its global objective z
1
i
as well as the local objective
z
2
i
. While the latter is locally defined at agent level,
the former is realized by a perceived context Γ
i
. For
the COHDA
2
heuristic, we replace this by a perceived
configuration Σ
i
. This does not change the problem
EvaluationofaSelf-organizingHeuristicforInterdependentDistributedSearchSpaces
27

description, but enables us to describe the interactions
of agents, and thus the ability to actually perceive in-
formation.
For that purpose, each agent a
i
maintains a config-
uration Σ
i
, which reflects the knowledge of a
i
about
the system. This configuration is initially empty, but
is updated during the iterative process through infor-
mation exchange with other agents. The COHDA
2
heuristic is inspired by swarming behavior, and de-
fines a local view on the system for each agent
through the use of neighborhood relations. This can
be expressed with a graph G = (V , E), where each
agent is represented by a vertex a
i
∈ V . Edges e =
(a
i
, a
k
) ∈ E depict communication links. Usually, this
graph is not fully connected. Thus, the neighborhood
of an agent a
i
is given by:
N
i
= {a
k
| (a
i
, a
k
) ∈ E} (4)
An agent may not communicate with any other agent
outside of its neighborhood. Just like flocking birds,
the agents now observe their local environment and
react to changes within their perception range. That
is, whenever an agent a
i
enters a new state
´
σ
i
by
changing the assignment of its decision variables x
i j
,
its neighboring agents a
k
∈ N
i
perceive this event.
These agents now each update their current local
view Σ
k
on the system, and react to this event by
re-evaluating their search spaces s
k
and subsequently
adapting their own decision variables. However, usu-
ally Σ
k
6= Σ
global
, hence an agent has to deal with in-
complete, local knowledge.
Thus, for improving the local search at agent level,
the COHDA
2
heuristic uses an information spread-
ing strategy besides this reactive adaptation. When-
ever a local change is published to the neighborhood,
the publishing agent a
i
includes information not only
about its updated state σ
i
, but about the currently
known configuration Σ
i
of all other agents it is aware
of as well. A receiving agent a
k
now updates its ex-
isting knowledge base Σ
k
with this two-fold informa-
tion (Σ
i
∪ {σ
i
}). In this update procedure, an element
σ
y
= hγ
y
, λ
y
i ∈ Σ
i
of the sending agent a
i
is added to
Σ
k
of the receiving agent a
k
if and only if any of the
following conditions hold:
1. Σ
k
does not already contain a state σ
z
with z = y,
such that
∀σ
z
∈ Σ
i
: z 6= y
2. Σ
k
already contains a state σ
z
with z = y, and σ
z
has a lower value λ
z
, such that
∃σ
z
= hγ
z
, λ
z
i ∈ Σ
i
: z = y ∧ λ
z
< λ
y
In this case, σ
y
replaces σ
z
in Σ
k
.
Using this information spreading strategy, agents
build a complete representation Σ
global
of the whole
system over time, and take this information into ac-
count in their decision making as well. However, due
to possibly rather long communication paths between
any two agents, these global views on the system are
likely to be outdated as soon as they are built and
represent beliefs about the systems rather than facts.
Nevertheless, they provide a valuable guide in the
search for optimal local decisions.
In order to ensure convergence and termination, a
third information flow is established on top of that.
In addition to the currently known system configura-
tion Σ
i
(including the agent’s own current state σ
i
),
each agent keeps track of the best known configura-
tion Σ
∗
i
= {σ
∗
i
, σ
∗
k
, . . . } it has seen during the whole
process so far. This is, whenever an agent updates its
Σ
i
by means of received information, it compares this
new configuration Σ
i
to Σ
∗
i
. If Σ
i
yields a better so-
lution quality than Σ
∗
i
according to DO-MC-COP (3),
Σ
i
is stored as new best known configuration Σ
∗
i
. In
addition to σ
i
and Σ
i
, an agent a
i
also exchanges its
Σ
∗
i
with its neighbors, everytime it changes. Thus,
when an agent a
k
receives a Σ
∗
i
from a neighbor a
i
,
the agent replaces its currently stored Σ
∗
k
by Σ
∗
i
, if the
latter yields a better solution quality than the former.
Similar to (Hinrichs et al., 2012), the whole pro-
cess can be summarized in the following three steps:
1. (update) An agent a
i
receives information from
one of its neighbors and imports it into its own
knowledge base. That is, its belief Σ
i
about the
current configuration of the system is updated, as
well as the best known configuration Σ
∗
i
.
2. (choose) The agent now adapts its own decision
variables x
i j
according to the newly received in-
formation, while taking its own local objectives
into account as well, scaled by the altruism pa-
rameter α
i
. If it is not able to improve the be-
lieved current system configuration Σ
i
, the state
σ
∗
i
stored in the currently best known configura-
tion Σ
∗
i
will be taken. The latter causes a
i
to revert
its current state σ
i
to a previous state σ
∗
i
, that once
yielded a better believed global solution.
3. (publish) Finally, the agent publishes its be-
lief about the current system configuration Σ
i
(in-
cluding its own new state
´
σ
i
), as well as the best
known configuration Σ
∗
i
to its neighbors. Local
objectives are not published to other agents, thus
maintaining privacy.
Accordingly, an agent a
i
has two behavioral options
after receiving data from a neighbor. First, a
i
will
try to improve the currently believed system config-
uration Σ
i
by choosing an appropriate w
i j
, and subse-
quently adding its new state
´
σ
i
to Σ
i
. Yet, this only
happens if the resulting Σ
i
would yield a better solu-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
28
tion quality than Σ
∗
i
. In that case, Σ
i
replaces Σ
∗
i
, so
that they are identical afterwards. If the agent can-
not improve Σ
i
over Σ
∗
i
, however, the agent reverts its
state to the one stored in Σ
∗
i
. This state, σ
∗
i
, is then
added to Σ
i
afterwards.
Thus, Σ
i
always reflects the current view of a
i
on
the system, while Σ
∗
i
always represents the currently
pursued goal of a
i
, since it is the best configuration the
agent knows. In either case, Σ
i
and Σ
∗
i
both contain
a
i
’s current state after step 2.
4 EMPIRICAL EVALUATION
We implemented the proposed heuristic COHDA
2
in
a multi-agent system (MAS). In our simulation en-
vironment, agents communicate asynchronously, us-
ing a network layer as communication backend. This
backend may be a physical one, so as to be able to dis-
tribute the MAS over arbitrary machines. In our eval-
uation however, we used a simulated network layer,
in order to have full control over message travelling
times, and to permit deterministic repetitions of sim-
ulation runs. For this, we used predefined seeds for
the random number generators. This allows us to
simulate unsteady communication layers with varying
message delays. Basically, our simulation is event-
driven. However, an event at agent level (i.e. the
adaptation procedure as described in the previous sec-
tion) is only triggered through a message by another
agent. Hence we may call the minimal time, that
it takes in principle for a message to be transferred
from the sender to the receiver, a simulation step. We
set this minimal possible message delay to 1 rather
than 0, since a message cannot be received instantly in
any physical communication network, no matter how
fast it is. In particular, this means that a simulation
step refers to one simulated unit of time, so that a
sent message will be received in the next simulation
step at the earliest (depending on its delay induced
by the communication backend). Our implementation
ensured that we were able to monitor all exchanged
messages.
In the following experiments, each agent repre-
sents a simulated combined heat and power (CHP)
device with an 800 l thermal buffer store. We used the
simulation model of an EcoPower CHP as described
in (Bremer and Sonnenschein, 2012). For each of
those devices, the thermal demand for a four-family
house during winter was simulated according to (Jor-
dan and Vajen, 2001). The devices were operated in
heat driven operation and thus primarily had to com-
pensate the simulated thermal demand. Additionally,
after shutting down, a device would have to stay off
for at least two hours. However, due to their thermal
buffer store and the ability to modulate the electrical
power output within the range of [1.3kW, 4.7 kW], the
devices had still some degrees of freedom left.
Since we are focusing on combinatorial problems
in the contribution at hand, for each conducted exper-
iment a set of feasible electrical power output profiles
was pre-generated from this simulation model. That
is, the simulation model has been instantiated with a
random initial temperature level of the thermal buffer
store and a randomly generated thermal demand, for
each CHP device separately. Subsequently, a num-
ber of feasible power profiles were generated from
each of these simulation models. The resulting sets of
power profiles are then used as local search spaces by
the agents. The global goal c of the optimization prob-
lem was generated as a random electrical power pro-
file, which was scaled to be feasible for the given pop-
ulation of CHP devices. However, we cannot guaran-
tee that an optimal solution actually lies within in the
set of randomly enumerated search spaces. The task
of the agents now was to select one element out of
their given sets of power profiles each, so that the sum
of all selected power profiles approximates the target
profile c as exactly as possible.
4.1 General Behavior
As a first step, we examined the general behavior of
the heuristic. In Figure 1, the results of a single sim-
ulation run (m = 30 devices with n = 2000 possible
power profiles each) are visualized. The planning
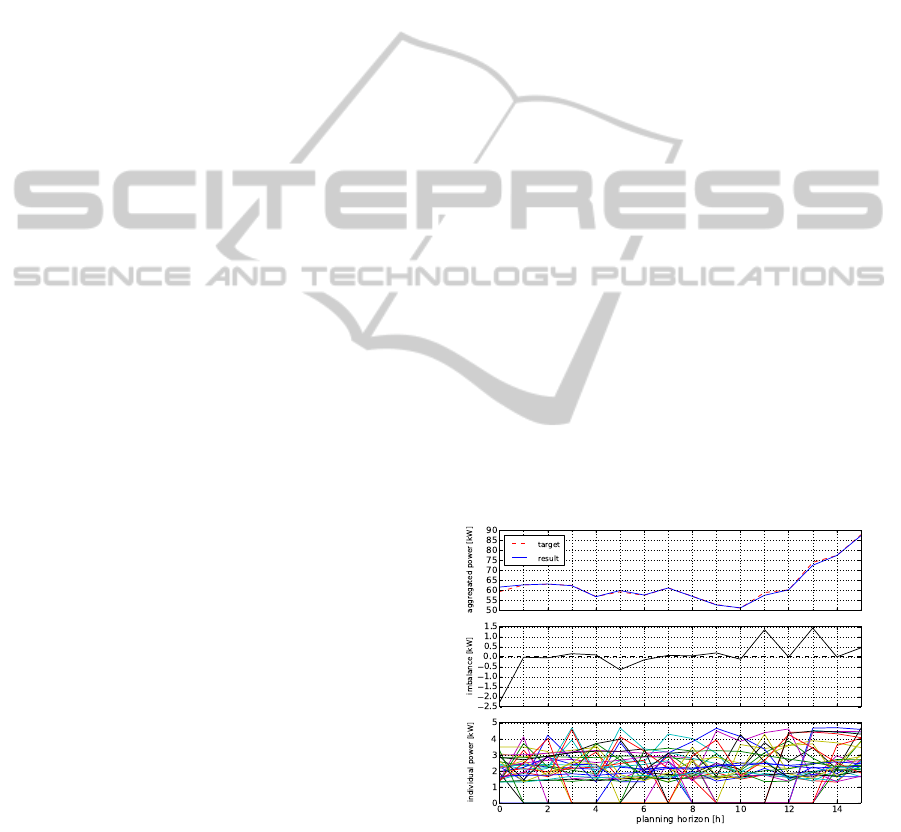
Figure 1: Optimization result of a single simulation run with
30 CHP (and local search spaces comprising 2000 feasible
power profiles each), for a planning horizon of four hours
in 15-minute intervals.
horizon was set to four hours in 15-minute intervals.
The upper chart shows the target profile (dashed line)
and the resulting aggregated power output (solid line).
The remaining power imbalance is shown in the mid-
EvaluationofaSelf-organizingHeuristicforInterdependentDistributedSearchSpaces
29
dle chart, while the individual power output profiles
of the devices are depicted in the lower chart. The
latter is quite chaotic, which is due to the limited sets
of available power output profiles per device. Nev-
ertheless, the heuristic was able to select 30 profiles
(one for each device), whose sum approximates the
target profile with a remaining imbalance of less than
2.5kW per time step in the planning horizon.
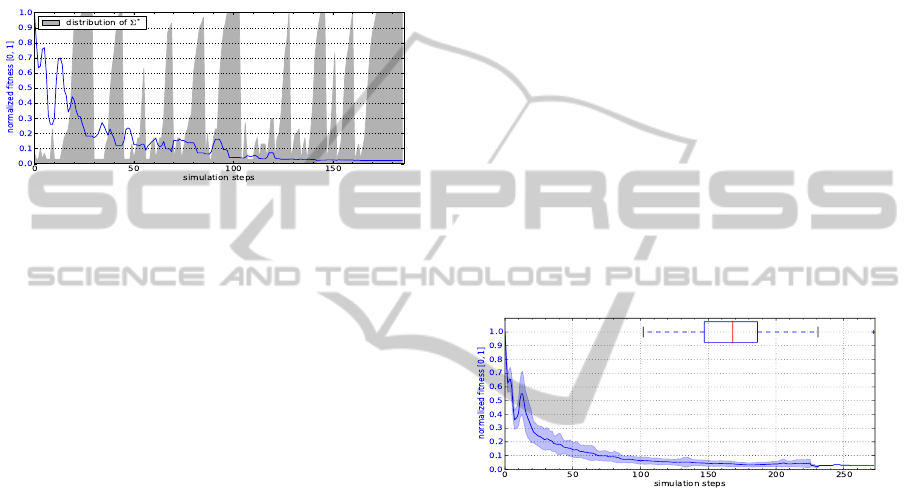
In Figure 2, the process of the heuristic for this
simulation run is shown in detail. This data is visible
Figure 2: Detailed illustration of the COHDA
2
heuristic
during a simulation.
to the simulation observer only, the individual agents
still act upon local knowledge. The solid line depicts
the global fitness value of the heuristic over time. This
fitness represents the global solution quality accord-
ing to equation (3), but has been normalized to the
interval [0.0, 1.0], with 0.0 being the optimum. The
normalization was done by taking an approximation
for the worst combination of power profiles
d
worst
= max
d
c,
m
∑
i=1
w
i,min
!
, d
c,
m
∑
i=1
w
i,max
!!
as upper bound (with w
i,min
and w
i,max
being ele-
ments having the minimal/maximal value in class i),
and assuming the existence of an optimal solution
(no remaining imbalance) as lower bound. In order
to examine convergence, the agent population was
parametrized with the upper bound as initial solution.
In general, the fitness decreases over time until it
converges to a near-optimal solution. However, it is
not strictly decreasing: Temporary deteriorations (in-
crease of the fitness value, which means an increas-
ing imbalance) are produced due to the decentralized
nature of the heuristic. They can be explained with
the distribution ratios of locally best known configu-
rations Σ
∗
(see Section 3). For this we centrally ob-
served the Σ
∗
i
of every agent a
i
in the network. Out
of these sets, at each simulation step, we identified
the Σ
∗
which yielded the best overall solution quality,
and measured the relative frequency of occurence of
this particular Σ
∗
in the population. The filled area
shows this distribution (the higher, the more agents
are aware of this specific Σ
∗
). Recall that an agent a
i
inherits a received Σ
∗
k
from a neighbor a
k
if Σ
∗
k
yields
a better rating than the currently stored Σ
∗
i
of the agent
a
i
. Thus, a Σ
∗
with very good rating prevails and
spreads in the network, until a better rated Σ
∗
is found
somewhere. This effect can be seen during simula-
tion steps 10 to 30, for instance. As the distribution
of the currently best configuration, say Σ
∗
0
, rises, the
global fitness improves steadily. In simulation step
30, however, an even better configuration, say Σ
∗
1
, has
emerged somewhere, which begins to spread subse-
quently. As the agent population continually adapts
this new Σ
∗
1
, the fitness value temporarily deteriorates,
before it steadily improves from simulation step 35
on, until in simulation step 45 another configuration,
say Σ
∗
2
, is found somewhere, that yields a better fit-
ness than Σ
∗
1
. This process continues up to the point
where no better rated Σ
∗
can be found, and the heuris-
tic terminates after 185 simulation steps. The final
fitness value is 0.02, which amounts to a total remain-
ing imbalance of 7.09 kW (0.007% of the targeted
1004.13kW in total over the planning horizon).
Figure 3 shows the performance of the COHDA
2
heuristic under the same parametrization, aggregated
over 100 simulation runs. For each simulation run,
Figure 3: Aggregated performance of COHDA
2
over 100
simulation runs with 30 CHP (and local search spaces com-
prising 2000 feasible power profiles each), for a planning
horizon of four hours in 15-minute intervals.
the same CHP devices and thus the same local search
spaces were used, but the communication network
was initialized with different seeds for the random
number generator. This yielded a different commu-
nication graph in each run, as well as different gen-
erated message delays. The solid line represents the
mean fitness over time, while the shaded area around
this line depicts the standard deviation. Obviously, the
COHDA
2
heuristic is able to converge to near optimal
solutions independently from the underlying commu-
nication backend. On average over all 100 simulation
runs, each agent sent 1.5 ± 0.04 messages per simula-
tion step. The boxplot visualizes simulation lengths,
with 169.69 ± 28.38 being the mean.
4.2 Parameter Analysis
Subsequent to the inspection of the general behavior,
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
30
we examined a number of input parameters of the
heuristic with regard to simulation performance. The
latter can be measured in terms of (a) the resulting fit-
ness after termination, (b) the simulation length, or (c)
the average number of exchanged messages per agent
per simulation step during the process. So the influ-
ence of the input parameters on each of these numbers
(a-c) has been analyzed. Each examined configura-
tion was simulated 100 times. The presented results
show mean values as well as standard deviations of
the observed properties from these 100 simulations. If
not stated otherwise, the experiments were conducted
using a small world network topology with φ = 2.0
(see Section 4.2.2 for an explanation).
4.2.1 Message Delay
An important property of the simulated communi-
cation backend is its ability for delayed messages.
In order to evaluate the robustness of the heuristic
against a non-deterministic communication layer, we
tested the approach with different amounts of mes-
sage delays. To accomplish that, we defined an in-
terval [1, msg
max
], from which a random number is
generated for each sent message. The message is then
delayed for the according number of simulation steps.
We evaluated msg
max
∈ {1, 2, 5, 7, 10}.
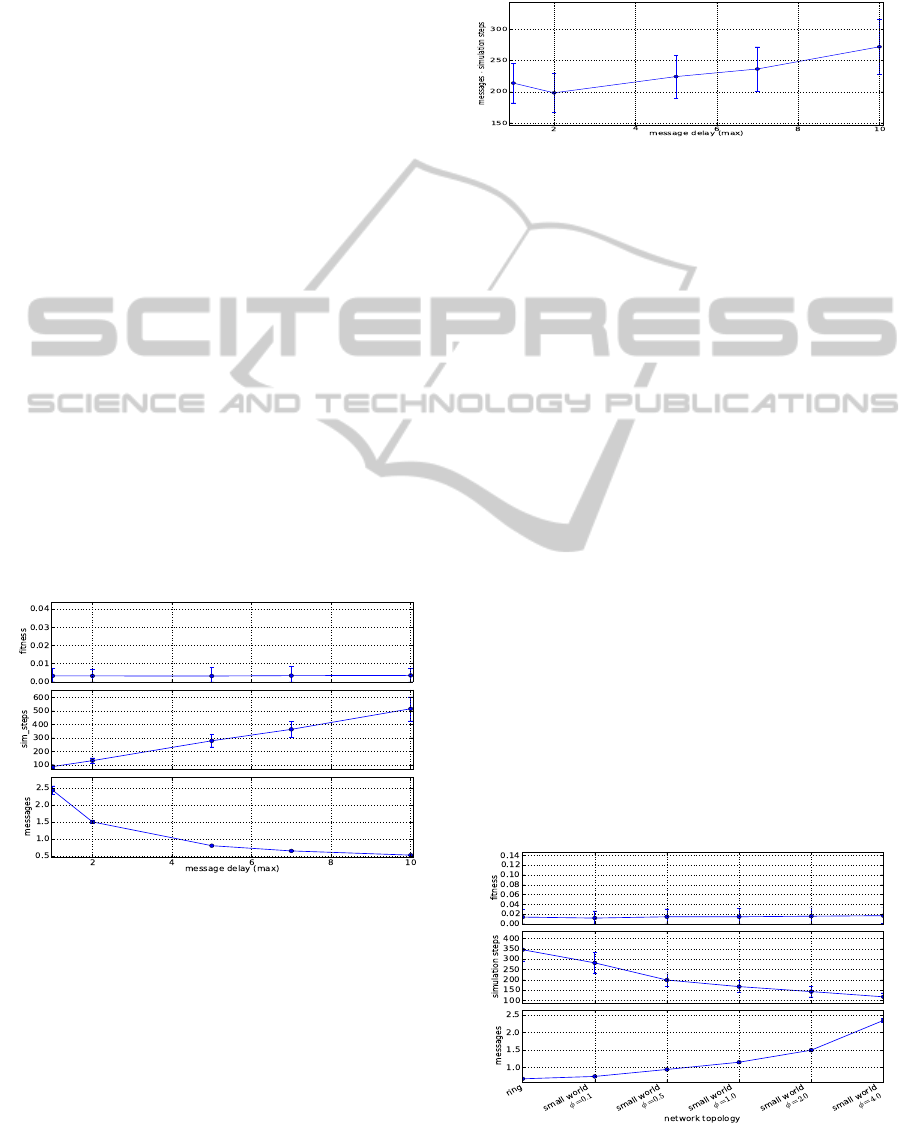
Figure 4 shows the influence of message delays
on the simulation performance, as defined in the pre-
vious paragraph (criteria a-c). Fortunately, message
Figure 4: Influence of different message delays.
delays have absolutely no influence on the final fit-
ness produced by the heuristic (criterion a, top chart).
This means that COHDA
2
is very stable against an
unsteady communication network. The time until ter-
mination (criterion b, middle chart) consequentially
rises linearly with increasing message delay. With re-
gard to the amount of exchanged messages (criterion
c, bottom chart), a strongly decreasing trend towards
less than one sent message on average per agent per
simulation step with increasing delay is visible. To re-
veal the best trade-off between simulation length and
communication overhead, Figure 5 shows the num-
ber of messages per agent throughout a whole simu-
lation run, depending on message delays. We find a
Figure 5: Influence of message delay on the sum of mes-
sages per agent for the whole simulation.
minimum of exchanged messages with msg
max
= 2.
Obviously, if compared to the absence of message de-
lays (msg
max
= 1), COHDA
2
does not only cope with,
but even benefits from a slight variation at agent level
introduced by message delays. However, in the ex-
amined scenario, this variation should be kept rather
small in order to speed up convergence. Thus, the fol-
lowing experiments were conducted using a message
delay msg
max
= 2.
4.2.2 Network Density
The composition of an agents’ neighborhood is
directly coupled to the underlying communication
graph G = (E, V ). Preliminary experiments showed
a beneficial impact of random graphs with a low di-
ameter. Thus, we evaluated the following topologies:
• Ring: The agents are inserted into a ring-shaped
list. Each agent is then connected to its predeces-
sor and successor.
• Small World: This network comprises an ordered
ring with |V | · φ additional connections between
randomly selected agents, cf. (Strogatz, 2001).
We examined φ ∈ {0.1, 0.5, 1.0, 2.0, 4.0}.
In Figure 6, the results of these experiments are visu-
alized. We ordered the plotted data according to the
Figure 6: Influence of the network topology.
EvaluationofaSelf-organizingHeuristicforInterdependentDistributedSearchSpaces
31
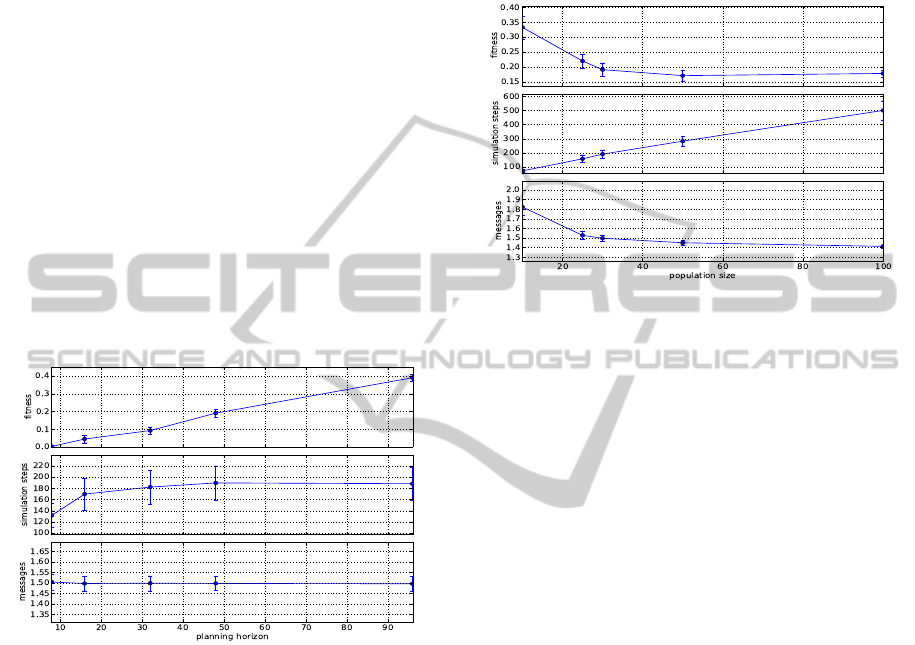
approximated average neighborhood size, which de-
fines the overall density of the communication graph.
Similar to the previous section, there is no influence of
the network density on solution quality. Expectedly,
the message complexity increases with larger neigh-
borhoods. Similarly, simulation length decreases with
more connections. Again the trade-off between run-
time in terms of simulation steps, and run-time in
terms of exchanged messages is visible. A compari-
son of the number of messages per agent throughout a
whole simulation run against network topology shows
that, for the given scenario, a small world topology
with φ = 0.5 yields the least messages on average dur-
ing a whole simulation (chart not shown here).
4.2.3 Planning Horizon
For real-world applications, it is interesting to know
what planning horizon the heuristic is capable of. Fig-
ure 7 shows the result of planning horizons with a
length of {2, 4, 8, 12, 24} hours in 15-minute inter-
vals. The final fitness in the upper chart deteriorates
Figure 7: Influence of the planning horizon.
almost linearly with larger planning horizons. Sim-
ilarly, the number of simulation steps rises, whereas
the number of exchanged messages is not influenced.
While we expected the last, we did not expect the in-
fluence of the planning horizon on fitness and sim-
ulation length, and examined it in more detail. After
several experiments with synthetic configurations (i.e.
carefully generated search space values according to
(Lust and Teghem, 2012)), it turned out to be a side
effect in our use of the CHP simulation models: Ran-
domly enumerating a rather small number of feasible
power profiles does not yield a sufficient coverage of
the theoretically feasible action space of the devices.
We found that increasing the size of pre-generated lo-
cal search spaces significantly improves the final sim-
ulation fitness again, while leaving the number of sim-
ulation steps and the number of exchanged messages
unaffected.
4.2.4 Population Size
Another interesting property regarding real-world ap-
plications is the influence of population size on the
heuristic. In Figure 8, a linear increase in simulation
steps until termination can be seen. This is conse-
Figure 8: Influence of the population size.
quently due to the increased coordination complex-
ity in larger networks. Yet, since the increase is lin-
ear at most, this shows that COHDA
2
is quite robust
against the number of participating individuals. In-
terestingly, the final fitness as well as the number of
exchanged messages per time step significantly im-
prove with larger population sizes. The former may
be related to the increased diversity, which could al-
ready be observed to be beneficial in the analysis of
the sizes of local search spaces in the previous sec-
tion. The latter can be attributed to an increased di-
ameter of the communication graph with larger pop-
ulation sizes. Here, information spreads more slowly,
and it takes a longer time for the system to converge.
4.3 Bi-objective Behavior
As described in Sections 2 and 3, we introduced lo-
cal objective functions at agent level for the COHDA
2
heuristic. As a proof of concept, we conducted an
experiment with randomly generated penalty values
p
i j
∈ [0, max(c)]. Figure 9 shows the aggregated re-
sults of 100 simulation runs, using 30 CHP appliances
with 200 feasible power profiles each, over a plan-
ning horizon of four hours, using a small world topol-
ogy with φ = 0.5 and a message delay msg
max
= 2.
The altruism parameter was set to α
i
= 0.5 for all
agents, so that the local objectives were considered
equally important to the global objective. The heuris-
tic is able to minimize local penalties to a normal-
ized value of 0.02 ± 0.01. Despite the rather difficult
setting of the altruism parameter, the global objective
fitness could effectively be optimized to a normalized
value of 0.15 ± 0.07, which amounts to a remaining
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
32
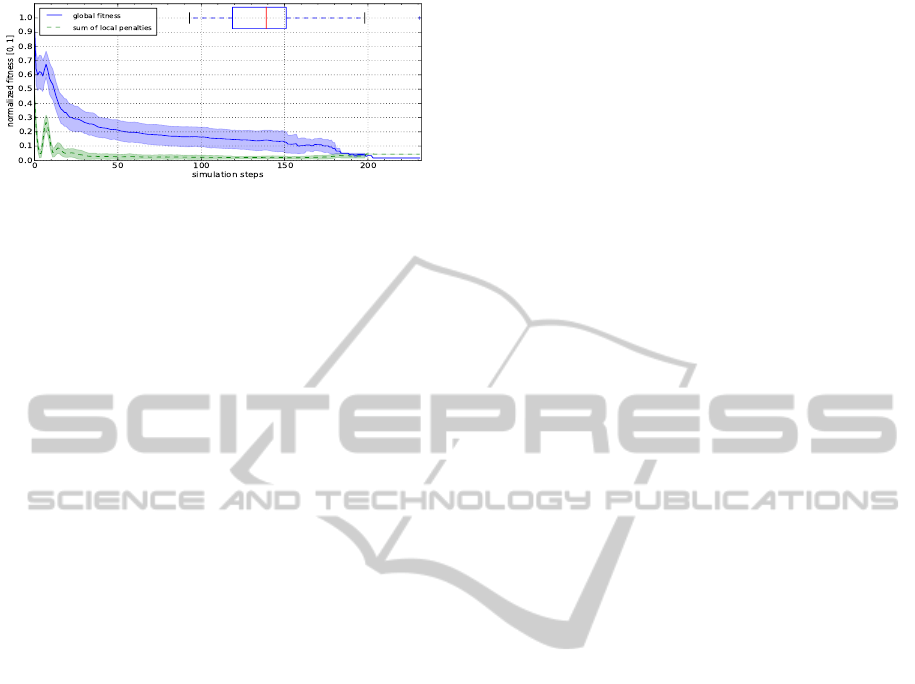
Figure 9: Aggregated performance of COHDA
2
over 100
simulation runs with distributed local objective functions
(∀i : α
i
= 0.5).
imbalance of 33.12kW ± 17.02 (0.06% ± 0.03 of the
targeted 544.26 kW in total over the planning hori-
zon).
5 RELATED WORK
The problem stated in this contribution is formulated
as an instance of a distributed constraint optimiza-
tion problem (DCOP). Algorithms for DCOP usu-
ally are optimal, i.e. they guarantee to find the op-
timal solution. The SynchBB approach introduced
by (Hirayama and Yokoo, 1997) incorporates a syn-
chronous branch&bound strategy and thus is quite
slow. ADOPT, as proposed in (Modi et al., 2005),
exploits inter-agent constraints to find an optimal so-
lution very efficiently. However, such a strategy is
not applicable to our problem setting, since every lo-
cal search space in principle depends on every other.
The constraint graph used in ADOPT would be fully
connected and hence would not provide any advan-
tage. (Penya, 2006) proposes COBB, a constraint op-
timization algorithm based on broadcasting. This ap-
proach is somewhat similar to COHDA
2
, we believe
however, that the information spreading approach in
COHDA
2
is more of a distributed nature than the
broadcasting used in the referenced work. Further,
COBB is a synchronous algorithm, whereas our ap-
proach is asynchronous and thus is truly decentral-
ized.
Regarding the smart grid domain, micro-
economic approaches are often used for distributed
problem solving. For example, the PowerMatcher
(Kok et al., 2005) incorporates a local price formation
process within a hierarchical structure. Here, the
optimization goal is the optimal dispatch of a traded
commodity. The approach has some major draw-
backs. First, it is statically organized with central
components, and thus is not truly decentralized.
Second, since the architecture solely specifies the
pricing mechanism, all decision complexity lies
within the bidding strategies of participating agents.
This applies to several other approaches of this kind
as well.
With respect to self-organizing systems, there are
a few interesting approaches with varying concepts.
In (Li et al., 2010), a semi-distributed system for solv-
ing distributed combinatorial optimization problems
is proposed. Similar to the COHDA
2
approach, au-
tonomous agents hold local search spaces and pur-
sue a common goal. Coordination, however, hap-
pens through a central, black-board like communi-
cation area called StigSpace. Thus, the approach is
not truly decentralized. (Pournaras et al., 2010) intro-
duces EPOS, a bottom-up planning algorithm using
a tree overlay organization structure. In contrast to
COHDA
2
, the EPOS approach imposes hierarchical
relations on the agents and thus again is not truly de-
centralized.
The applied methodology of cooperative problem
solving in COHDA
2
is quite similar to the AMAS ap-
proach, and especially to the AMAS4Opt agent model
as proposed in (Kaddoum, 2011). Therefore our con-
tribution focuses on a problem specific implementa-
tion rather than a general methodology.
6 CONCLUSIONS & FUTURE
WORK
In the contribution at hand, we presented COHDA
2
,
which is a self-organizing heuristic for solving dis-
tributed combinatorial optimization problems. We ap-
plied the heuristic to a problem from the smart grid
domain, and performed a thorough evaluation of the
performance under varying conditions. We imple-
mented an asynchronous multi-agent system with full
control over the communication backend. Regard-
ing our example application, it could be shown that
the heuristic exhibits convergence and termination,
and is robust against unsteady communication net-
works. The run-time of COHDA
2
, in terms of sim-
ulation steps, rises linearly with increasing popula-
tion sizes. Further, there is a trade-off between the
number of simulation steps until termination, and the
number of exchanged messages. This trade-off can
be adjusted through the density of the communication
network (i.e., the average size of the neighborhoods).
The evaluation of a bi-objective scenario showed the
ability of the heuristic to optimize local penalties as
well as a global objective in parallel.
In the present form, COHDA
2
needs a central op-
erator that broadcasts the optimization goal, and is
able to detect the termination of the process (and thus
has a global view on the system). But the actual
optimization process is still performed in a truly de-
EvaluationofaSelf-organizingHeuristicforInterdependentDistributedSearchSpaces
33

centralized manner! A fully decentralized variant of
COHDA
2
, however, could be realized by including
the ability to detect termination in a self-organizing
way, as well as the capability to spontaneously nomi-
nate a spokesperson from the population of agents, in
order to announce the optimization result.
An important future subject will be to study the in-
fluence of the altruism parameter on the heuristic, i.e.:
How does the resulting global fitness depend on the
setting of α
i
? If the agents are allowed to define this
value on their own, how can we guarantee that the sys-
tem does not collapse? Future work will also include
the analysis of adaptivity, i.e. spontaneously changing
decisions of agents in already converged configura-
tions, or repeatedly varying optimization targets. Ad-
ditionally, we will address the embedding of the math-
ematical representation of device’s action spaces, as
formulated in (Bremer and Sonnenschein, 2012), in
order to circumvent the currently existing premise of
enumerated local search spaces in COHDA
2
with its
disadvantages as described in Section 4.2.3.
ACKNOWLEDGEMENTS
Due to the vast amounts of simulations needed, all
experiments have been conducted on HERO, a multi-
purpose cluster installed at the University of Olden-
burg, Germany. We would like to thank the main-
tenance team from HERO for their valuable service.
We also thank Ontje L
¨
unsdorf for providing the asyn-
chronous message passing framework used in our
simulation environment, and J
¨
org Bremer for provid-
ing the CHP simulation model.
REFERENCES
Bremer, J. and Sonnenschein, M. (2012). A distributed
greedy algorithm for constraint-based scheduling of
energy resources. In SEN-MAS’2012 Workshop, Proc.
of the Federated Conference on Computer Science and
Information Systems, pages 1285–1292, Wrocław,
Poland. IEEE Catalog Number CFP1285N-ART.
Gellings, C. (2009). The Smart Grid: Enabling Energy Ef-
ficiency and Demand Response. The Fairmont Press,
Inc.
Gershenson, C. (2007). Design and Control of Self-
organizing Systems. Copit-Arxives.
Hinrichs, C., Lehnhoff, S., and Sonnenschein, M. (2012).
A Decentralized Heuristic for Multiple-Choice Com-
binatorial Optimization Problems. In Operations
Research Proceedings 2012 – Selected Papers of
the International Conference on Operations Research
(OR 2012), Hannover, Germany. Springer.
Hirayama, K. and Yokoo, M. (1997). Distributed Partial
Constraint Satisfaction Problem. In Principles and
Practice of Constraint Programming, pages 222–236.
H
¨
olldobler, B. and Wilson, E. O. (1990). The Ants. Belknap
Press of Harvard University Press.
Jones, J. C., Myerscough, M. R., Graham, S., and Oldroyd,
B. P. (2004). Honey bee nest thermoregulation: di-
versity promotes stability. Science (New York, N.Y.),
305(5682):402–4.
Jordan, U. and Vajen, K. (2001). Influence Of The DHW
Load Profile On The Fractional Energy Savings: A
Case Study Of A Solar Combi-System With TRNSYS
Simulations. Solar Energy, 69:197–208.
Kaddoum, E. (2011). Optimization under Constraints
of Distributed Complex Problems using Cooperative
Self-Organization. Phd thesis, Universit
´
e de Toulouse.
Kok, J. K., Warmer, C. J., and Kamphuis, I. G. (2005). Pow-
erMatcher. In Proceedings of the fourth international
joint conference on Autonomous agents and multia-
gent systems - AAMAS ’05, page 75, New York, New
York, USA. ACM Press.
Kroeker, K. L. (2011). Biology-inspired networking. Com-
munications of the ACM, 54(6):11.
Li, J., Poulton, G., and James, G. (2010). Coordination of
Distributed Energy Resource Agents. Applied Artifi-
cial Intelligence, 24(5):351–380.
Lust, T. and Teghem, J. (2012). The multiobjective multi-
dimensional knapsack problem: a survey and a new
approach. International Transactions in Operational
Research, 19(4):495–520.
Modi, P., Shen, W., Tambe, M., and Yokoo, M. (2005).
ADOPT: Asynchronous Distributed Constraint Opti-
mization with Quality Guarantees. Artificial Intelli-
gence, 161(1-2):149–180.
Penya, Y. (2006). Optimal Allocation and Scheduling of
Demand in Deregulated Energy Markets. Phd, Vienna
University of Technology.
Pournaras, E., Warnier, M., and Brazier, F. M. (2010). Local
agent-based self-stabilisation in global resource utili-
sation. International Journal of Autonomic Comput-
ing, 1(4):350.
Reynolds, C. W. (1987). Flocks, herds and schools: A
distributed behavioral model. SIGGRAPH Comput.
Graph., 21(4):25–34.
Serugendo, G., Gleizes, M.-P., and Karageorgos, A. (2005).
Self-organisation in multi-agent systems. The Knowl-
edge Engineering Review, 20(2):65–189.
Strogatz, S. H. (2001). Exploring Complex Networks. Na-
ture, 410(March):268–276.
Tero, A., Takagi, S., Saigusa, T., Ito, K., Bebber, D. P.,
Fricker, M. D., Yumiki, K., Kobayashi, R., and Nak-
agaki, T. (2010). Rules for biologically inspired
adaptive network design. Science (New York, N.Y.),
327(5964):439–42.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
34
