
Fourier Spectral of PalmCode as Descriptor for Palmprint Recognition
Meiru Mu
1,2
, Qiuqi Ruan
1
, Luuk Spreeuwers
2
and Raymond Veldhuis
2
1
Institute of Information Science, Beijing Jiaotong University, Beijing, China
2
Signals and Systems group, University of Twente, Enschede, The Netherlands
Keywords:
Gabor Filtering, Palm Code, Fourier Spectral, Horizontal and Vertical 2DPCA, Palmprint Recognition.
Abstract:
Study on automatic person recognition by palmprint is currently a hot topic. In this paper, we propose a
novel palmprint recognition method by transforming the typical palmprint phase code feature into its Fourier
frequency domain. The resulting real-valued Fourier spectral features are further processed by horizontal
and vertical 2DPCA method, which proves highly efficient in terms of computational complexity, storage
requirement and recognition accuracy. This paper also gives a contrast study on palm code and competitive
code under the proposed feature extraction framework. Besides, experimental results on the Hongkong PolyU
Palmprint database demonstrate that the proposed method outperforms many currently reported local Gabor
pattern approaches for palmprint recognition.
1 INTRODUCTION
Nowadays, recognition of individuals by means of
biometric characteristics is becoming increasingly fa-
miliar and accepted. The selection of biometrics is
commonly application-dependent (D. Zhang, 2004;
S. Pankanti et al., 2000). Palmprint, extracted from
person’s hand, has been recognized as a means of
measurement that can uniquely represent a person
(W. Shu et al., 1998b). It has been a long history
since the palmprints found on the crime scene were
used for forensic investigation. Recently, palmprint
is being investigated intensively for personal recog-
nition in different real-time application system, such
as access control, network security, and social secu-
rity. Compared with the fingerprints, palmprints have
more rich features which are less likely to be de-
stroyed and forged. Besides, palmprints can be cap-
tured with a much lower resolution imaging sensor
(less than 100 dpi), which leads to be more efficient
(W. Shu et al., 1998a). The online palmprint capture
devices are mainly based on CCD camera or digi-
tal scanner. More recently, the real time multispec-
tral palmprint capture device has also been developed
(R.K. Rowe et al., 2007; Z. Guo et al., 2010). In
addition to the efficient palmprint acquisition, robust
palmprint representation is another key issue for the
success of palmprint recognition application.
The algorithms proposed for online palmprint
recognition (including verification and identification),
are generally divided into three main classes: sub-
space learning methods, texture energy feature extrac-
tion, and coding based methods. Among them, coding
based methods are deemed to be the most promising
due to their high recognition accuracy and small fea-
ture size, which typically involve steps of filter bank
selection, coding scheme design and template match-
ing approach. The popular filters include Gabor,
Gaussian, and other self-designed ones. The phase,
orientation, and magnitude information are generally
regarded as encoded objects. The coding rules are
usually flexible and simple, and the obtained code fea-
tures should be robust and provide high discriminative
ability. PalmCode (D. Zhang et al., 2003) encodes the
phase of Gabor filtered responses into binary features.
FusionCode (A. Kong et al., 2006) used a fusion rule
at feature layer to further improve PalmCode. DoG
code method (X.Q. Wu et al., 2006) first convolves
the image using two-dimensional Gaussian filter and
then encodes the zero-crossing information of hori-
zontal and vertical gradient values, respectively. Or-
dinalCode (Z.N. Sun et al., 2005) encodes the outputs
of the elliptical Gaussian filters. The schemes encod-
ing the orientation of palm lines are also popular due
to its stability which includes competitive code (Com-
pCode) (A. Kong et al., 2004), binary orientation co-
occurrence vector (BOCV) code (Z. Guo et al., 2009),
palmprint orientation code (POC) (X.Q. Wu et al.,
2005), robust line orientation code (RLOC) (W. Jia
et al., 2008), and so on (F. Yue et al., 2009; W. Zuo
22
Mu M., Ruan Q., Spreeuwers L. and Veldhuis R. (2013).
Fourier Spectral of PalmCode as Descriptor for Palmprint Recognition.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 22-32
DOI: 10.5220/0004228000220032
Copyright
c
SciTePress

et al., 2010). However, coding based methods re-
quire the pixel-to-pixel paired matching between en-
rollment and query templates. In order to offset the
inter-class translation variation, one template has to
be shifted in some range and the matching score com-
putation is proceeded multiple times to finally deter-
mine the identity of one query palmprint, which is
time costly. Refer to Ref. (D. Zhang, 2004), the
matching speed of PalmCode is 1.7 ms when the sys-
tem works under the verification mode and the algo-
rithm is implemented in Visual C++ 6.0 on a PC using
Intel Pentium III processor (500MHZ). For identifi-
cation, if the database contains 100 persons and three
palmprint images are registered for each subject, the
total identification time is about 1.1s. As can be seen,
the matching speed of coding based methods is not
desirable for the identification system with large reg-
istered database. This issue has also been addressed
in some other reported literatures. In order to deal
with it, Jia (W. Jia et al., 2008) applied Tensor LPP on
their extracted directional representation. However, it
can not provide translation invariant performance by
reducing the dimension of integer codes directly. Yue
(F. Yue et al., 2011) proposed an approach to speed
up the coding based palmprint recognition method by
building a template tree to perform fast nearest neigh-
bor searching. For both of these methods, the final
classification is still based on pixel-to-pixel code tem-
plate matching by Hamming distance.
Accordingly, in this paper, we aim to further study
the code features for palmprint representation. The
following three issues are mainly considered:
Firstly, about the filter selection, Gabor, Gaussian,
and the second derivative of Gaussian filter have been
evaluated based on several coding based methods in
Ref. (F. Yue et al., 2008) and their experimental re-
sults show that the Gabor filter is superior. Besides, it
is well known that Gabor representation can provide
optimal localization of image details in a joint spatial
and frequency domain (J. Beck, 1987). Concerning
these conclusions, the Gabor filters are chosen for our
proposed feature extraction method in this paper.
Secondly, about the encoded object, we employ
the phase information. Gabor phase, as a discrimi-
nating information source, has been successfully used
in pattern recognition field. Besides PalmCode and
IrisCode, kinds of local Gabor phase pattern opera-
tors (W. Zhang et al., 2009; B. Zhang et al., 2007;
S. Xie et al., 2010) are proposed as well based on the
combination of the spatial histogram and the Gabor
phase pattern encoding scheme. These methods in-
volve a group of Gabor filters (in general 40 Gabor
filters) to extract the multi-scale and multi-orientation
information, which is an overcomplete representation
with a high redundant ratio. The high dimensional-
ity of the local Gabor phase pattern histograms leads
to high computational cost and large storage require-
ment. To deal with this problem, this paper proposes a
new method, which uses only two Gabor filters while
provides higher recognition performance.
Thirdly, instead of representing palmprint image
by the code features directly, we transform the code
feature matrices into their Fourier frequency fields
since a shift in the time domain causes no change
in the Fourier magnitude spectrum. The resulting
spectral features not only keep the property of pow-
erful discriminative ability of PalmCode features, but
also make it possible to extend the application field
of coding based features. Because the dissimilarity
measurement of the original coding based features is
generally based on pixel-to-pixel matching by using
Hamming or angular distances, which limits their ap-
plication to unsupervised template matching mode,
while the real-valued spectral features might be pro-
cessed further by the currently reported supervised
learning algorithms, which probably achieves higher
recognition performance.
PalmCode DFT
Horizontal
2DPCA
Vertical
2DPCA
Palm
Figure 1: Flow chart of the proposed method. (DFT - dis-
crete Fourier transform; 2DPCA - two-dimensional princi-
ple components analysis).
Taking all the above factors into consideration,
a novel Fourier spectral representation of PalmCode
(DFT PalmCode) is proposed for palmprint recog-
nition in this paper, whose flow chart is shown in
Fig. 1. We firstly transform the typical palmprint
phase code feature into its Fourier frequency domain
by discrete Fourier transform (DFT). The resulting
real-valued Fourier spectral features are then pro-
cessed by the horizontal and vertical two-dimensional
principal component analysis ((2D)
2
PCA) method.
The translation invariant property of Fourier trans-
form and (2D)
2
PCA dimensionality reduction method
help alleviating the within-class image translations
to some extent. Compared with the original Palm-
Code method, the proposed feature extraction ap-
proach operates two pairs of Gabor filtering phase
responses, which improves the recognition perfor-
mance evidently. This paper also gives a contrast
study on CompCode under the proposed feature ex-
traction framework. For CompCode, palm line orien-
tation information is encoded into bits. Furthermore,
our experimental results demonstrate that the pro-
posed method outperforms many currently reported
local Gabor pattern operators for palmprint recogni-
tion by higher accuracy, lower computational cost and
FourierSpectralofPalmCodeasDescriptorforPalmprintRecognition
23

less storage requirement.
This paper is organized as follows. In section 2,
we give a short review of PalmCode. Section 3 il-
lustrates the proposed Fourier spectral representation
in details. In section 4, the (2D)
2
PCA method is de-
scribed for the dimensional reduction of the proposed
spectral features, which helps alleviating the negative
effects due to image translation. The experimental re-
sults will be demonstrated in section 5. The final part
is about the conclusions.
2 REVIEW OF PalmCode
The Gabor phase quadrant demodulation coding
method is proposed by Daugman for iris recogni-
tion in 1993 (J. Daugman, 1993), which is then
reported successful for palmprint representation in
Ref. (W.K. Kong et al., 2003). For ease of presen-
tation, this feature extraction method is commonly
named by IrisCode, PalmCode or Daugman’s method.
For PalmCode, a circular 2-D Gabor filter is used
to firstly convolve the original gray palmprint image,
which has the following general form:
g(x,y,u,θ,σ) =
1
2πσ
2
exp
{
−(x
2
+ y
2
)
2σ
2
}
×exp{2πi(uxcosθ + uy sin θ)}.
(1)
Where i =
√
−1, u is the frequency of the sinusoidal
wave along the direction θ from the x-axis, and σ
specifies the Gaussian envelope along x and y axes,
which determines the bandwidth of the Gabor filter.
In practice, a Gabor function with a special set of
parameters {u, θ, σ}, is transformed into a discrete
Gabor filter. In order to provide more robustness to
brightness, the Gabor filter is turned to zero direct
current (DC) denoted by ˜g(x,y). Following the ex-
perimental setting in Ref. (W.K. Kong et al., 2003), σ
is set to 5.6179.
Given an image f (x,y) of size M ×N, its Gabor
filtered images are defined as:
G(x,y) =
∑
x
1
∑
y
1
f (x
1
,y
1
) · ˜g(x −x
1
,y −y
1
). (2)
Where G(x,y) is complex number with real part
Re
(G(x,y)) and imaginary part
Im
(G(x,y)).
Assuming the Gabor parameters {θ,u,σ} are
given, PalmCode method encodes each pixel in the
Gabor filtered image into two bits by the following
rules:
P
Re
(x,y) =
{
0,
if Re
(G(x,y)) < 0;
1,
otherwise
.
(3)
P
Im
(x,y) =
{
0,
if Im
(G(x,y)) < 0;
1,
otherwise
.
(4)
Where P
Re
(x,y) and P
Im
(x,y) are respectively the en-
coded real and imaginary binary feature templates.
3 FOURIER SPECTRAL OF
PalmCode
The discrete Fourier transform (DFT) of a func-
tion (image) p(x, y) of size M ×N can be given by
P(u,v) = |P(u,v)|e
ϕ(u,v)
, where |P(u,v)|= [R
2
(u,v)+
I
2
(u,v)]
1/2
is called the magnitude spectrum of the
Fourier transform, and ϕ(u,v) = tan
−1
[
I(u,v)
R(u,v)
]
is
called the phase angle or phase spectrum of the trans-
form. R(u,v) and I(u,v) are the real and imaginary
parts of F(u,v), respectively.
The Fourier transform has the following transla-
tion properties:
If p(x, y) ⇔ P(u,v),
then
p(x −x
0
,y
0
) ⇔ P(u, v)e
−j2π(ux
0
/M+vy
0
/N)
(5)
and
p(x,y)(−1)
x+y
⇔ P(u −M/2,v −N/2) . (6)
Equation (5) tells us that a shift in the time domain
causes no changes in the magnitude spectrum but only
the changes in the phase spectrum of Fourier trans-
form. This property has been widely used to ex-
tract translation invariant features in pattern recogni-
tion. Equation (6) describes that multiplying p(x, y)
by (−1)
x+y
shifts the original of P(u,v) to frequency
coordinates (M/2,N/2), which is the center of the
M ×N area occupied by the 2-D DFT. This result is
based on the variables u and v having values in the
range [0, M −1] and [0,N −1], respectively. In a com-
puter implementation these variables will run from
u = 1 to M and v = 1 to N, in which case the ac-
tual center of the transform will be at u = M/2 + 1
and v = N/2 + 1. This property is usually used when
visualizing the 2-D Fourier spectrum.
The DFT has the following conjugate symmetry
property:
P(u,v) = P
∗
(−u,−v), (7)
from which it follows that the spectrum is symmetric
about the original:
|P(u,v)| = |P(−u,−v)|. (8)
Based on the symmetry property, we can only keep
half of the Fourier coefficients for image representa-
tion.
Figure 2 gives an illustration of the proposed
Fourier spectral representation scheme. Figure 2(a)
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
24

One Gabor
filter
Real part
Imaginary
part
(a)
PalmCode Fourier spectral
(b) (c) (d)
DFT
DFT
(e) (f)
Figure 2: An illustration of the proposed Fourier spectral representation scheme. (a) original image; (b) PalmCode; (c)
PalmCode down-sampled by ratio of 2:1; (d) Palmcode with the four rows and columns along the code plane edges set to 0;
(e) Fourier spectral of (d); (f) half of (e).
shows a typical palmprint image from PolyU palm-
print database. Figure 2(b) visualizes the original
PalmCode feature planes as illustrated in section 2.
For reducing the computational cost, the PalmCode
features are down-sampled by the ratio of 2:1 in this
study, as can be seen from Fig. 2(c). On the edge
of the code matrices, there are usually some non-
palmprint features resulted from defective image pre-
processing. For reducing their affects, some masks
are generally needed in the classical coding based
methods (D. Zhang et al., 2003; A. Kong et al., 2004).
While in the proposed method, the values of four rows
and columns along the code plane edges are changed
into zeros for removing the non-palmprint pixels, as
Fig. 2(d) shows. Figure 2(e) shows the Fourier spec-
tral features of PalmCode with the center coordinate
(33,33). It is quite obvious that the Fourier spectral
matrix is symmetric with respect to the center point.
Thus, only half of the spectral values are required for
further processing. Figure 2(f) shows half of the spec-
tral features, which is the final Fourier spectral repre-
sentation of our proposed.
4 SPECTRAL FEATURE
REDUCTION BY (2D)
2
PCA
The Fourier spectral feature of PalmCode consists
of several real-valued matrices size of 31×64, as
shown in Fig. 2(f). The large dimensionality leads
to high computational cost, limited matching speed
and costly template storage requirement. In order to
cope with these problems, we resort to (2D)
2
PCA di-
mensional reduction technique (X. Pan et al., 2008),
which is called Modified 2DPCA (D. Zhang et al.,
2009) or horizontal and vertical 2DPCA method
(J. Yang et al., 2007) in some other papers. The
(2D)
2
PCA method not only helps saving the com-
putational cost and providing smaller feature space,
but also has a useful invariance property: the trans-
form matrix of horizontal 2DPCA is invariant to any
change of image row sequence, and the transform ma-
trix of vertical 2DPCA is invariant to any change of
an image column sequence. This invariance property
of (2D)
2
PCA helps alleviating the negative effect re-
sulting from image translation (J. Yang et al., 2007).
Taking these factors into consideration, (2D)
2
PCA
method is sequently carried out on the Fourier spec-
tral feature space.
Given N spectral feature X
1
,X
2
,...,X
N
, each spec-
tral X
i
(i = 1,2,...,N) is a m ×n matrix, the goal
of horizontal 2DPCA is to find the optimal orthog-
onal projection axes U so that the projected matrices
Y = [Y
1
,Y
2
,...,Y
N
] achieve a maximum total scatter,
which can be expressed in the form:
Y
i
= X
i
U, i = 1, 2, . . . , N (9a)
U = arg(max(tr(S
Y
))), (9b)
where
tr(S
Y
) = U
T
S
X
U (10a)
S
Y
=
1
N
N
∑
j=1
(Y
j
−
¯
Y )(Y
j
−
¯
Y )
T
(10b)
S
X
=
1
N
N
∑
j=1
(X
j
−
¯
X)
T
(X
j
−
¯
X) , (10c)
It follows that S
X
is a non-negative definite matrix
size of n × n. In general, the optimal projection
axes U = [u
1
,u
2
,...,u
d
] are chosen as the orthogonal
eigenvectors of S
X
corresponding to the largest eigen-
values λ
1
,λ
2
,...,λ
d
. Thus the projected vectors are
d-dimensional. Finally, after processed by the hori-
zontal 2DPCA, each spectral matrix is represented as
a matrix Y
i
of dimension m ×d (d ≪ n).
After the procedure of horizontal 2DPCA trans-
form, the correlation between row vectors of spectral
feature matrices is removed, and the resulted projec-
tion matrices are less sensitive to the translation and
FourierSpectralofPalmCodeasDescriptorforPalmprintRecognition
25

mirror variations of the spectral row sequences. Fur-
ther, the vertical 2DPCA transform is needed to re-
move the correlation between column vectors of the
projected matrices Y
i
.
For simplify, the horizontal 2DPCA transform is
processed on the transpose of the projected matrices,
denoted by Y
T
i
(i = 1,2,...,N). Then the correspond-
ing total scatter matrix can be expressed in the form:
C
Y
T
=
1
N
N
∑
j=1
(Y
T
j
−
¯
Y
T
)
T
(Y
T
j
−
¯
Y
T
)
=
1
N
N
∑
j=1
(Y
j
−
¯
Y )(Y
j
−
¯
Y )
T
,
(11)
which is a non-negative definite matrix size of m ×m.
Let V = [v
1
,v
2
,...,v
q
] be the orthogonal eigenvec-
tors of C
Y
T
corresponding to the largest eigenvalues
γ
1
,γ
2
,...,γ
q
(q ≪m). By letting R represent the pro-
jected matrices of Y after the vertical 2DPCA trans-
form, we have R
T
is the projected matrices of Y
T
after
the horizontal 2DPCA transform, that is
R
T
= Y
T
V . (12)
It follows that
R = (Y
T
V )
T
= V
T
Y = V
T
XU, R ∈ R
q×d
. (13)
As can be seen, the dimensionality of the Fourier
spectral feature X is reduced from m × n to q ×d
(d ≪ n, q ≪ m) after the (2D)
2
PCA transform.
As Fig. 2 shows, each image generates two spec-
tral feature matrices when one Gabor filter is con-
volved. Based on the proposed feature extraction
framework, we might obtain more robust feature rep-
resentation for palmprint recognition, if more Gabor
filters with different orientations are used. As a mat-
ter of fact, we find that the proposed method performs
much better when two Gabor filters instead of one are
used for spectral feature extraction according to the
experimental results. Figure 3 illustrates the training
steps of the proposed algorithm when two Gabor fil-
ters are used, in accordance with which we summarize
the proposed palmprint feature extraction algorithm
as follows:
Step 1. Input the training palmprint images, and con-
volve each image with two Gabor filters of
different orientation parameters to obtain four
PalmCode matrices.
Step 2. Perform the 2-D Fourier transform on each
binary PalmCode matrix to get the corre-
sponding spectral feature matrix as described
in Fig. 2.
Step 3. Perform (2D)
2
PCA transform on these spec-
tral feature matrices got in Step 2 to obtain the
Gabor
filter1
(2D)
2
PCA
Real part1
Gabor
filter2
Training
samples
Imaginary
part1
Real part2
Imaginary
part2
1U
1V
and
2U
2V
and
3U
3V
4U
4V
and
and
Fourier spectral
of PalmCode
Projection
of matrices
(2D)
2
PCA
(2D)
2
PCA
(2D)
2
PCA
Figure 3: The training steps of the proposed algorithm when
two Gabor filters are used. The Fourier spectral of Palm-
Code is achieved as illustrated in Fig. 2.
corresponding four groups of feature projec-
tion matrices (V 1,U1), (V 2,U2), (V 3,U3),
(V 4,U4) as shown in Fig. 3.
Step 4. Transform the four Fourier spectral matrices
of each training image by the four groups
of feature projection matrices respectively to
generate four feature matrices as described in
Eq. (13), denoted by {R1,R2,R3,R4}. Save
them as the training feature database.
Step 5. When a query image is captured, the same
processing as Steps 1 and 2 is applied, and
then transform their Fourier spectral matri-
ces as Step 4 to get the final feature template
{R1
′
,R2
′
,R3
′
,R4
′
}.
Step 6. For template matching, the training and
test feature matrices are respectively con-
verted into vectors {R1,R2, R3, R4} and
{R1
′
,R2
′
,R3
′
,R4
′
}; Then the dissimilarity is
measured by sum of Euclidean distance be-
tween each pair of vectors Ri and Ri
′
, which
can be denoted by
∑
4
i=1
D(Ri,Ri
′
).
1(a) 2(a) 3(a)
1(b) 2(b) 3(b)
4(a) 5(a)
4(b) 5(b)
Figure 4: The palmprint images in the Hong Kong PolyU
database. (a) Samples in session one; (b) Samples in session
two.
5 EXPERIMENTAL RESULTS
In this section, we evaluate the recognition perfor-
mance of our proposed method using HongKong
Polytechnic University (PolyU) Palmprint Database,
which contains 7752 grayscale images in BMP image
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
26

2 4 6 8 10
96.5
97
97.5
98
98.5
99
99.5
100
Ten cases with different Gabor orientation settings
Identification accuracy (%)
One Gabor filter
Two Gabor filters
Three Gabor filters
Figure 5: The identification accuracies (%) versus the ten
Gabor orientation setting cases.
format. They were captured by CCD camera from
386 different palms and collected in two occasions
with different illumination conditions. The interval
between the two sessions is about two months. Each
person provided around ten palmprint images from
the left and right hands respectively. The resolution of
original captured images is 384×284 pixels at 75 dpi.
By performing the similar preprocessing approach de-
scribed in Ref. (W.K. Kong et al., 2003), we cropped
the region of interest (ROI) size of 128×128. Figure 4
shows the cropped images from five typical palm sam-
ples, in which (a) and (b) denote the samples captured
from the same palm at the first and second sessions
respectively.
5.1 Determination of the Parameters
For the Gabor based methods, there is generally a
set of adjustable parameters. For DFT PalmCode
method, Besides Gabor parameters, d and q for
(2D)
2
PCA transform are controllable as well. In this
group of experiments, we firstly calculate the values d
and q by taking 90% of the total sum of the eigenval-
ues. Based on the obtained values d and q, a series of
experiments is carried out to investigate the influence
of Gabor orientation parameter and examine how the
number of Gabor filters affects the identification rate.
Secondly, with the determined optimal Gabor filters,
the identification accuracies are investigated as d and
q vary.
For each palm, five samples from session one are
randomly collected to construct the training set, and
all the samples (in total 3863) captured in session two
are used for testing. Assuming the system is operated
in the identification mode (one-to-many comparison).
The average correctness rate (%) of ten-run identifi-
cation executions is used to evaluate the identification
performance.
By following the experimental results of literature
(W.K. Kong et al., 2003), the Gabor parameter u is
set to 0.0916, and σ is fixed to 5.6179. In order to
determine the optimal number of Gabor filters and
their orientation parameters for our proposed method,
16 18 20 22 24 26 28 30 32 34 36 38
99.45
99.5
99.55
99.6
99.65
99.7
99.75
99.8
The projected vector dimension d of the horizontal 2DPCA
Identification accuracy (%)
q=10
q=12
q=14
q=16
q=18
q=20
q=22
Figure 6: Identification rates (%) as values d and q vary.
we test some orientation cases on palmprint identi-
fication accuracy. For the applied (2D)
2
PCA trans-
form, values d and q are determined by taking 90%
of the total sum of eigenvalues. When one Gabor
filter is used, the considered orientation values are
0
◦
, 10
◦
, 30
◦
, 45
◦
, 60
◦
, 90
◦
, 120
◦
, 135
◦
, 150
◦
, and
170
◦
, respectively. Besides, the identification rates
are also investigated when two and three Gabor fil-
ters are used with ten cases of different orientation
settings. The tested orientation groups are as follows:
{45
◦
, 60
◦
}, {45
◦
, 90
◦
}, {45
◦
, 120
◦
}, {45
◦
, 135
◦
},
{60
◦
, 90
◦
}, {60
◦
, 120
◦
}, {60
◦
, 135
◦
}, {90
◦
, 120
◦
},
{90
◦
, 135
◦
}, {120
◦
, 135
◦
}, {45
◦
,60
◦
, 90
◦
}, {45
◦
,
60
◦
, 120
◦
}, {45
◦
, 60
◦
,135
◦
}, {45
◦
, 90
◦
, 120
◦
}, {45
◦
,
90
◦
, 135
◦
}, {45
◦
, 120
◦
, 135
◦
}, {60
◦
, 90
◦
, 120
◦
},
{60
◦
, 90
◦
, 135
◦
}, {60
◦
, 120
◦
, 135
◦
}, {90
◦
, 120
◦
,
135
◦
}. Figure 5 gives an illustration of the relation-
ship between the identification accuracies and the Ga-
bor orientation parameters. As it shows, the recogni-
tion performances of the proposed method improve
when the Gabor filter number increases from two to
three in most cases. However, the increase of Gabor
filter numbers adds to the computational cost in multi-
ple. Based on an overall consideration of the recogni-
tion performance and the computational complexity,
case 6 with two Gabor filters is determined to be op-
timum. That is to say, our proposed method achieves
the highest identification rate 99.74% when two Ga-
bor filters with the orientation parameters of 60
◦
and
120
◦
respectively are used for the spectral feature ex-
traction on the PolyU palmprint database.
Given the Gabor parameters we got above, the op-
timal values d and q for (2D)
2
PCA are experimen-
tally investigated by varying q from 10 to 22 and d
from 16 to 38. The identification rates correspond-
ing to different d and q are plotted in Fig. 6. As can
be seen, the best identification rate of our proposed
method is close to 99.8%. The feature dimension af-
ter (2D)
2
PCA transform is q ×d, which is expected to
FourierSpectralofPalmCodeasDescriptorforPalmprintRecognition
27

Table 1: Comparisons of the average identification accuracy (%), time cost (s) for identifying per test sample, and the verifi-
cation EER (%).
Method Identification accuracy (%) Time cost (s) Verification EER (%)
PalmCode 0 75.63 0.067 29.5
PalmCode [-1,1] 95.14 0.644 9.1
PalmCode [-2,2] 98.27 1.66 3.1
DFT PalmCode 99.74 0.123 0.7
CompCode 0 78.14 0.085 24.2
CompCode [-1,1] 96.17 0.920 7.2
CompCode [-2,2] 99.11 2.398 1.9
DFT CompCode 99.29 0.106 0.9
as small as possible while keeping the highest identi-
fication rate. Therefore, the best identification perfor-
mance is obtained when d = 28, q = 12, as can be
seen from Fig. 6.
It should be pointed out that in other experiments
we simply take the sum of the largest d eigenvalues
that determine 90% of the total sum of the eigen-
values when processing the horizontal 2DPCA trans-
form. By the same way, we get the value of q for the
vertical 2DPCA transform.
5.2 Comparisons with Coding Methods
In this section the palmprint identification and ver-
ification performances are investigated when Palm-
Code is replaced by the CompCode, which I denote
by DFT CompCode. For PalmCode, the used Gabor
filter parameters are given by u = 0.0916, θ = π/4,
and σ = 5.6179; For CompCode, six Gabor filters are
used to obtain the competitive code features with the
orientation set as θ
j
= π j/6, j = 0,1,...,5. u and σ
are fixed to 0.0916 and 5.6179 respectively; All the
code features mentioned here are down-sampled by
ratio of 4:1. For obtaining the matching distance, the
code feature matrix needs to be shifted by rows and
columns. Here the shifting ranges are set to 0, [-1,1]
and [-2,2]. Time cost for identifying per test sam-
ple is recorded by Matlab 7.5 from a personal com-
puter with an Intel Pentium(R) Dual-Core Processor
(E5200@2.50GHz) and 2GB RAM configured with
Microsoft Windows XP.
When the system works in the identification mode,
five samples from session one are randomly collected
to construct the training set, and all the samples from
session two are used for testing. The average identi-
fication rates (%) of ten-run executions with different
methods are listed in Table 1. Besides, the time cost
of identifying one test sample is also compared un-
der the current data set. When the system operates in
the verification mode, all the 7752 samples are used.
Each palmprint template is matched with all the other
ones to evaluate the receiver operating characteristics
(ROC). A genuine matching is defined as the match-
ing between the features from the same palm, and oth-
erwise the matching is counted as an impostor. The
total number of matches is 30 042 876, of which the
number of genuine is 74 068 and the number of im-
postor is 29 968 808.
Table 1 shows the comparisons of the average
identification accuracy (%), time cost (s) for identi-
fying per test sample, and the verification EER (%).
As can be seen, the recognition performance of cod-
ing based methods depends badly on the transla-
tion extent of code feature plane. Furthermore, the
matching speed dramatically drops as the translation
range increases. The identification rate of CompCode
achieves 99.11% at the time cost of 2.398 seconds,
which is not desirable when the system is operated
in the identification mode. DFT PalmCode outper-
forms PalmCode significantly in terms of identifica-
tion performance and verification accuracy because of
two reasons. First, DFT PalmCode fuses more phase
information from two Gabor filters with different ori-
entations, instead of one Gabor filtering as Palm-
Code exploits, which makes the discriminative ability
more powerful. Second, using the frequency-domain
representation of code features makes it capable of
undergoing training process by some learning algo-
rithms, which improves the recognition performance
and also reduces the time cost of dissimilarity calcu-
lation. By comparing the identification performances
of CompCode and DFT CompCode, it can be seen
that the identification accuracy does not improve ev-
idently while the matching speed drops dramatically
after executing DFT transform and (2D)
2
PCA on the
code features. This may be because the processes of
DFT transform and (2D)
2
PCA do not extract more
discriminative information from the image, but their
resulting real-valued feature templates cost less than
the logical-valued code feature planes. From Table 1
it can be also seen that lower EER is achieved by op-
erating the DFT and (2D)
2
PCA transform on the code
features. Since the matching score measurements for
coding based methods and the proposed feature repre-
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
28
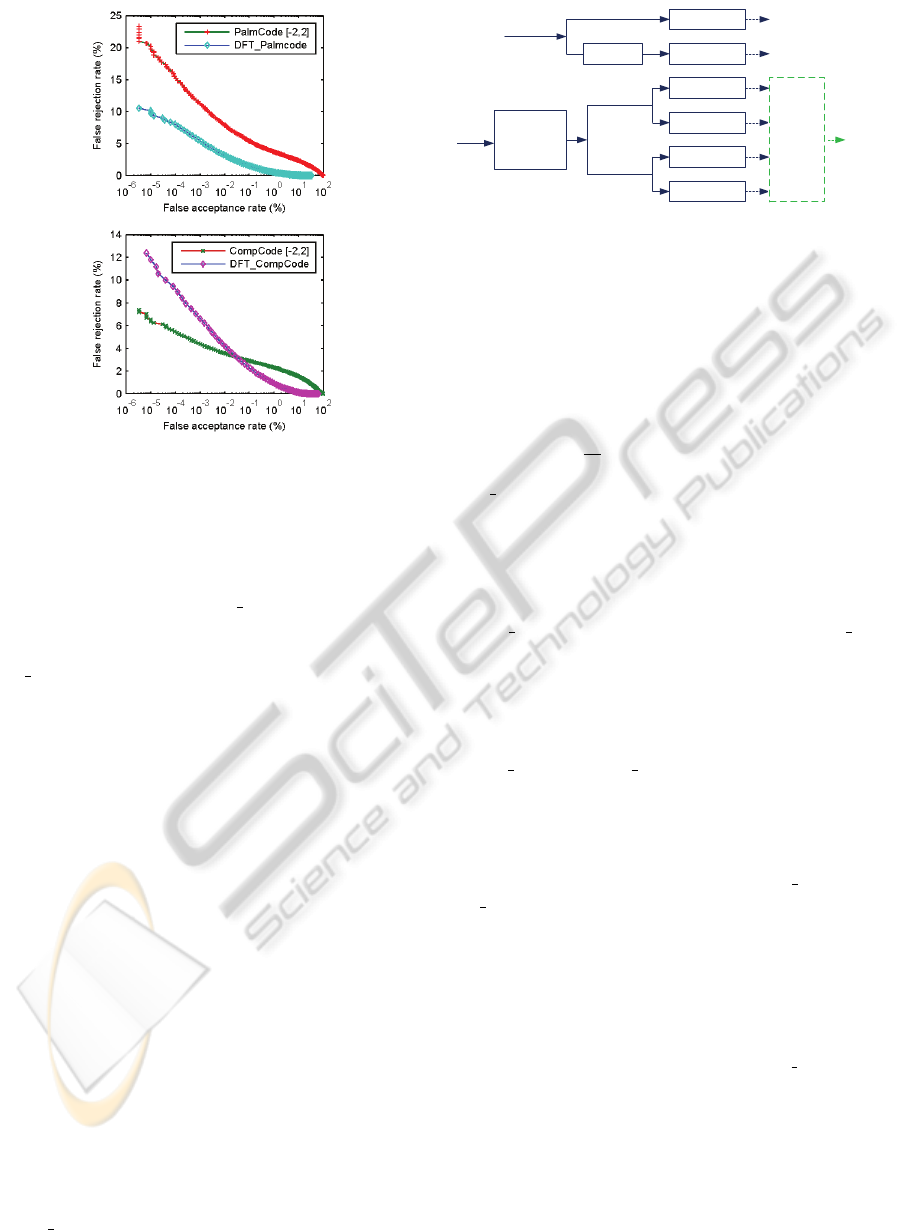
(a)
(b)
Figure 7: Comparison of the verification accuracies (%)
(FAR versus FRR). For the coding based methods, the code
template is shifted horizontally and vertically for multiple
times within a range [-2, 2].
sentation framework are totally different, we plot their
ROC curves for comparisons further. From Fig. 7(a)
and (b), we can see that DFT CompCode does not
improve the verification accuracy of CompCode ab-
solutely though it does achieve lower EER. However,
DFT PalmCode does perform much better than Palm-
Code.
5.3 Comparisons with other Methods
Gabor filtering based methods have been widely in-
vestigated in various image representation field. Be-
sides coding based methods, there are two other
classes: First, Gabor coefficients based statistical
learning methods, which make the statistical analy-
sis of the Gabor magnitude coefficients (R. Chu et al.,
2007; X. Pan et al., 2008; X. Pan et al., 2009; M. Mu
et al., 2011); Second, local Gabor pattern histogram
methods (W. Zhang et al., 2009; B. Zhang et al., 2007;
S. Xie et al., 2010; W.C. Zhang et al., 2005), which
fuse the Gabor coefficients with different local pat-
tern operators to achieve histogram sequences as de-
scriptors. In this section, comparisons with some of
them are evaluated on the palmprint recognition per-
formance. Note that for principal component analy-
sis (PCA) and linear discriminant analysis (LDA) in-
volved in these methods, we take the sum of the first
largest eigenvalues that determine 90% of the total
sum of the eigenvalues for fair comparisons.
GM (2D)
2
PCA (X. Pan et al., 2008), as a repre-
sentative method of Gabor coefficients based statisti-
Phase
quadrant
demodulation
coding
LXP
LXP
Concatenating
Concatenating
Real code
Imaginary
code
Gabor
part
Re_LGPP
Im_LGPP
Re_GGPP
Im_GGPP
HGPP
LBP
Gabor
phase
LGBP_Phase
Quantizing LBP LGXP
Figure 8: An illustration of various local pattern operators
compared in this paper. (LBP - local binary pattern, LXP -
local XOR pattern).
cal learning methods, is compared in this group of ex-
periments. A bank of five-scale and eight-directional
filters (in total 40 filters) is firstly used to derive a
Gabor feature space of high dimensionality and then
two steps of 2DPCA as described in section 4 are car-
ried out to reduce the dimension. The Gabor param-
eters are set as follows: θ
j
= π j/8, j = 0,1,...,7,
u
v
= 0.2592/
√
2
v
, v = 0, 1, . . . ,4, σ = 5.6179. For
GM (2D)
2
PCA method, the Gabor coefficients are
down-sampled by the ratio of 4:1. Otherwise, the Ga-
bor feature dimensionality will be too high to be pro-
cessed further in our experimental system.
By encoding Gabor magnitude and phase co-
efficients via local binary pattern (LBP) operator,
LGBP Mag (W.C. Zhang et al., 2005) and LGBP Pha
(W. Zhang et al., 2009) have been proposed respec-
tively. By using the local XOR pattern (LXP) oper-
ator to encode the real and imaginary parts of Gabor
complex response, local Gabor phase pattern (LGPP)
has been proposed (B. Zhang et al., 2007), denoted
by Re LGPP and Im LGPP respectively. Different
from LGPP, GGPP has been proposed to represent
orientation patterns, which forms one eight-bit binary
string to represent each pixel by concatenating the real
or imaginary quadrant-bit codes of different orienta-
tions for a given frequency (denoted by Re GGPP and
Im GGPP). In addition, Xie (S. Xie et al., 2010) pro-
posed local Gabor XOR pattern (LGXP) by quantiz-
ing the Gabor phase in each local region firstly, and
then encoding the quantized phases by LXP operator.
Figure 8 gives an illustration of different local Gabor
pattern operators. For fair comparisons, the Gabor pa-
rameters used in all the mentioned local Gabor pattern
methods are the same as those set in GM (2D)
2
PCA
method.
We assume that the system works in the identifi-
cation mode, samples from session one are used for
training, and all the samples from session two for
test. Different training sets are constructed respec-
tively with the sample numbers of each palmprint
class ranging from two to five. The training samples
are randomly selected and ten-run executions are av-
FourierSpectralofPalmCodeasDescriptorforPalmprintRecognition
29

Table 2: Comparisons of the average identification accuracy (%) and feature length among different methods. For evaluating
the identification performance, the training sample number per class ranges from two to five. The average identification rate
is calculated over ten-run executions with various training and testing sets.
Method
Identification rate (%) Gabor
number
Feature length
before reduction
Final
feature length5 4 3 2
DFT PalmCode 99.74 99.67 99.55 99.24 2 7 936 2 878
GM (2D)
2
PCA 81.42 80.34 77.65 74.84 40 40 960 13 680
Re LGPP 97.10 96.87 96.20 94.18 40 40 960 1 540
Im LGPP 97.22 97.10 96.56 95.48 40 40 960 1 540
HGPP 98.40 98.11 97.93 97.82 40 92 160 1 540
LGBP Phase 97.75 97.57 97.08 95.92 40 40 960 1 540
LGXP 98.24 97.97 97.42 97.15 40 40 960 1 540
eraged to evaluate the identification rate (%). Besides,
the resulting feature size is also investigated for eval-
uating the computational complexity.
Table 2 lists the comparisons of palmprint iden-
tification performance. As it shows, the proposed
method achieves the highest identification rate by
a large margin. Even under the condition of
less training samples, the identification accuracy of
DFT PalmCode method reaches up to 99.24%. Dif-
ferent from the other Gabor based methods, which ex-
tract multi-scale and multi-directional features using
40 Gabor filters, DFT PalmCode uses only two Gabor
filters. Since the Gabor filtering is time-costing, less
used filters leads to the advantages of higher execu-
tion speed and lower storage requirement. Besides, all
the local Gabor pattern methods generate a histogram
feature space with high dimensionality. As the num-
ber of resulting sub-blocks increases, the histogram
dimension will extend in multiple. Given the sub-
block number be N, and the image class number C,
then the final feature vector length will be N ×(C −1).
As Table 2 shows, N ×(C −1) = 4×(386−1) = 1540
is the final feature size of the mentioned local Gabor
pattern methods in this group of experiments, while
the final feature length of DFT PalmCode is 2878,
which is larger but still comparable.
6 CONCLUSIONS
In this paper, we have presented a new feature ex-
traction method for palmprint recognition. The Gabor
phase information is firstly encoded into binary code
features, which are then transformed into Fourier
spectral (denoted by DFT PalmCode) as palmprint
descriptor. The spectral features are further processed
by the horizontal and vertical 2DPCA transform for
palmprint recognition. Experimental results demon-
strate its high efficiency under both verification and
identification system mode.
The main contributions and conclusions of this pa-
per are as follows: (1) The proposed method is related
to the original PalmCode approach, but they are quite
different. First, the real-valued spectral features are
achieved for palmprint recognition instead of the bi-
nary code matrices, which not only keep the high dis-
criminative ability of PalmCode features, but also can
be processed by some learning algorithms to further
improve the recognition performance. Second, due
to the translational invariance property of Fourier and
(2D)
2
PCA transform, DFT PalmCode method over-
comes the weakness of pixel-to-pixel matching strat-
egy, which is widely applied by the coding based
methods as well as PalmCode. Third, under the pro-
posed feature extraction framework, more than one
Gabor filters can be utilized to fuse phase informa-
tion, which improves the recognition accuracy evi-
dently compared with PalmCode. (2) The contrast
experimental results between another coding method
and our method demonstrate that the proposed feature
extraction framework can be used on other code-plane
based features for increasing identification speed as
well as PalmCode. (3) Compared with other state-
of-the-art Gabor phase based methods which gener-
ally use 40 Gabor filters, the proposed method greatly
outperforms in terms of recognition accuracy, compu-
tational complexity and storage requirement by using
only two Gabor filters.
ACKNOWLEDGEMENTS
This work is supported partly by the National Grand
Fundamental Research 973 Program of China un-
der Grant No. 2004CB318005, and the Fundamen-
tal Research Funds for the Central Universities (Grant
No. KKJB11034536).
REFERENCES
Kong, A. and Zhang, D. (Aug. 23-26, 2004). Competitive
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
30

coding scheme for palmprint verification. In Proc.
17th Int. Conf. Pattern Recognition (ICPR’04), pages
520–523, Cambridge, UK.
Kong, A. and Zhang, D. and Kamel, M. (2006). Palm-
print identication using feature-level fusion,. Pattern
Recognition, 39(3):478–487.
Zhang, B. and Shan, S. and Chen, X. and Gao, W. (2007).
Histogram of gabor phase patterns (hgpp): A novel
object representation approach for face recognition.
IEEE Trans. image process., 16:57–68.
Han, D. and Guo, Z. and Zhang, D. (Oct.26-29, 2008). Mul-
tispectral palmprint recognition using wavelet-based
image fusion. In Proc. Int. Conf. Signal Processing,
pages 2074–2077, Beijing,China.
Zhang, D. and Kong, A. and You, J. and Wong, M. (2003).
Online palmprint identification. IEEE Trans. Pattern.
Anal. Mach. Intell., 25(9):1041–1050.
Zhang, D. and You, X. and Wang, P. and Yanushkevich,
S. N. and Tang, Y. (2009). Facial biometrics using
nontensor product wavelet and 2d discriminant tech-
niques. Int. J. Patt. Recog. Art. Intel., 23(3):521–543.
Daugman, J. (1993). High confidence visual recognition
of persons by a test of statistical independence. IEEE
Trans. Pattern Anal. Mach. Intell., 15(11):1148–1161.
Yue, F. and Zuo, W. and et al.. (2011). Fast palmprint iden-
tification with multiple templates per subject. Pattern
Recognition Letters, 32:1108–1118.
Yue, F. and Zuo, W. and Zhang, D. and Wang, K. (2009).
Orientation selection using modified fcm for competi-
tive code-based palmprint recognition. Pattern Recog-
nition, 42(11):2841–2849.
Yue, F. and Zuo, W. and Wang, K. and Zhang, D. (Jun.
24-26, 2008). A performance evaluation of filter de-
sign and coding schemes for palmprint recognition.
In Proc. 19th Int. Conf. Pattern Recognition (ICPR),
pages 1–4.
Beck, J. and Sutter, A. and Ivry, R. (1987). Spatial fre-
quency channels and perceptual grouping in texture
segmentation. Computer Vision, Graphics, Image
Processing, 37(1987):299–325.
Yang, J. and Liu, C. (2007). Horizontal and vertical 2dpca-
based discriminant analysis for face verification on a
large-scale database. IEEE Transactions on Informa-
tion Forensics and Security, 2(4):781–792.
Mu, M. and Ruan, Q. (2011). Mean and standard deviation
as features for palmprint recognition based on gabor
filters. Int. J. Patt. Recog. Art. Intel., 25(4):491–512.
Chu, R. and Lei, Z. and Han, Y. and He, R. and Li, S. Z.
(Nov.18-22, 2007). Learning gabor magnitude fea-
tures for palmprint recognition. In Proc. 8th Asian
Conf. Computer Vision (ACCV2007), pages 22–31,
Tokyo, Japan.
Rowe, R. K. and Uludag, U. and Demirkus, M. and
Parthasaradhi, S. and Jain, A. K. (Sept.11-13, 2007).
A multispectral whole-hand biometric authentication
system. In Proc. Biometrics Symposium, pages 1–6,
Baltimore, MD.
Pankanti, S. and Bolle, R. M. and Jain, A. K. (2000). Bio-
metrics: The future of identification. IEEE Computer,
33(2):46–49.
Xie, S. and Shan, S. and Chen, X. and Chen, J. (2010).
Fusing local patterns of gabor magnitude and phase
for face recognition. IEEE Trans. Image Process.,
19(5):1349–1361.
Jia, W. and Huang, D. and Tao, D. and Zhang, D. (12-15
Oct. 2008). Palmprint identification based on direc-
tional representation. In Proc. IEEE Int. Conf. Sys-
tems, Man and Cybernetics (SMC2008), pages 1562–
1567, Singapore.
Jia, W. and Huang, D. S. and Zhang, D. (2008). Palmprint
verification based on robust line orientation code. Pat-
tern Recognition, 41(5):1521–1530.
Shu, W. and Zhang, D. (1998a). Automated personal
identification by palmprint. Optical Engineering,
37(8):2659–2362.
Shu, W. and Zhang, D. (Aug.16-20,1998b). Palmprint veri-
fication: An implementation of biometric technology.
In Proc. 14th Int. Conf. Pattern Recogn., pages 219–
221, Brisbane,Australia.
Zhang, W. and Shan, S. and Chen, X. and Gao, W. (2009).
Are gabor phases really useless for face recognition?
Pattern Analysis & Applications, 12(3):301–307.
Zuo, W. and Lin, Z. and Guo, Z. and Zhang, D. (Jun.13-
18, 2010). The multiscale competitive code via sparse
representation for palmprint verification. In Proc.
23rd IEEE Int. Conf. Computer Vision and Pattern
Recognition (CVPR), pages 2265–2272, San Fran-
cisco, CA, USA.
Zhang, W. C. and Shan, S. G. and Gao, W. and Zhang,
H. M. (Oct.17-21, 2005). Local gabor binary pattern
histogram sequence (lgbphs): A novel non-statistical
model for face representation and recognition. In
Proc. 10th Int. Conf. Computer Vision, volume 1,
pages 786–791, Beijing, China.
Kong, W. K. and Zhang, D. and Li, W. (2003). Palm-
print feature extraction using 2-d gabor filters. Pattern
Recognition, 36(10):2339–2347.
Pan, X. and Ruan, Q. (2008). Palmprint recognition using
gabor feature-based (2d)
2
pca. Neurocomputing Let-
ters, 71(13-15):3032–3036.
Pan, X. and Ruan, Q. (2009). Palmprint recognition using
gabor-based local ivariant features. Neurocomputing
Letters, 72(7-9):2040–2045.
Wu, X. Q. and Wang, K. Q. and Zhang, D. (2005). Palm-
print authentication based on orientation code match-
ing. in: AVBPA 2005, Lecture Notes in Computer Sci-
ence, 3546:555–562.
Wu, X. Q. and Wang, K. Q. and Zhang, D. (Nov.3-6, 2006).
Palmprint texture analysis using derivative of gaussian
filters. In in: Proc. IEEE Int. Conf. Computational In-
telligence and Security, pages 751–754, Guangzhou,
China.
Hao, Y. and Sun, Z. and Tan, T. (Nov.18-22, 2007). Com-
parative studies on multispectral palm image fusion
for biometrics. In Proc. 8th Asian Conference on
Computer Vision (ACCV), pages 12–21, Tokyo, Japan.
Guo, Z. and Zhang, L. and Zhang, D. (Aug. 23-26, 2010).
Feature band selection for multispectral palmprint
recognition. In Proc. 20th Int. Conf. Pattern Recog-
nition (ICPR), pages 1136-1139.
FourierSpectralofPalmCodeasDescriptorforPalmprintRecognition
31

Guo, Z. and Zhang, D. and Zhang, L. and Zuo, W.
(2009). Palmprint verification using binary orienta-
tion co-occurrence vector. Pattern Recognition Let-
ters, 30:1219–1227.
Guo, Z. H. and Lu, G. M. (July 11-14, 2010). Palmprint
recognition using gabor magnitude code. In Proc.
IEEE Int. Conf. Machine Learning and Cybernetics
(ICMLC), volume 2, pages 796–801, Qingdao, China.
Zhang, D. (2004). Palmprint Authentication. Kluwer Aca-
demic Publication, Dordrecht.
Sun, Z. N. and Tan, T. N. and Wang, Y. H. and Li, S. Z.
(Jun.25, 2005). Ordinal palmprint representation for
personal identification. In Proc. IEEE Int. Conf. Com-
puter Vision and Pattern Recognition, San Diego, CA,
USA.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
32
