
SMQT-based Tone Mapping Operators for High Dynamic Range Images
Mikael Nilsson
Centre of Mathematical Sciences, Lund University, Lund, Sweden
Keywords:
Tone Mapping Operation, High Dynamic Range, Successive Mean Quantization Transform, Processing Speed.
Abstract:
In this paper, tone mapping operations based on the nonlinear Successive Mean Quantization Transform
(SMQT) are proposed in order to convert high dynamic range images to low dynamic range images. A SMQT-
based tone mapping applied on the luminance channel is derived as well as a SMQT-based method working
directly on all RGB channels. Both methods are compared to other state-of-the-art methods and produce visu-
ally similar results. The processing speeds of the SMQT-based methods are discussed and found to be some
of the fastest reported on a single CPU. Furthermore, additional improvement regarding the processing speed
and its impact on image quality is investigated.
1 INTRODUCTION
The real world scenes we experience in our daily life
have a very wide range of luminance values. The
human visual system is capable of perceiving scenes
over five orders of magnitude and can gradually adapt
to scenes with dynamic ranges of over nine orders
of magnitude (Duan and Qiu, 2004). While humans
can perceive scenes over five orders the current con-
sumer products today typically has display and acqui-
sition technology ranging from two to three orders of
magnitude. Hence, pursuing High Dynamic Range
(HDR) images is of interest in order to reduce the
discrepancy between consumer products and human
perception. Recent trends in HDR imaging research
involves design of HDR imaging sensors, HDR im-
age generation techniques, encoding methods for effi-
cient transmission and algorithms designed to display
HDR images on Low Dynamic Range (LDR) devices
(Bandoh et al., 2010; Barakat et al., 2008; Lu et al.,
2009). Tone Mapping Operation (TMO) is the pro-
cess of converting an HDR image to an LDR image.
The task of such a TMO needs to address the issue of
finding a good balance between emphasizing all fea-
tures in the image as well as presenting a good con-
trast while producing the LDR image. Several recent
proposed TMOs can be found in the literature (Chen
et al., 2005; Duan and Qiu, 2004; Liu et al., 2010;
Lee et al., 2010; Qiu et al., 2010; Kuang et al., 2007;
Meylan and Susstrunk, 2006; Reinhard et al., 2002;
Reinhard and Devlin, 2005; Mantiuk et al., 2008; Du-
rand and Dorsey, 2002; Drago et al., 2003; Pattanaik
et al., 2000).
TMOs can generally be divided into two broad
categories: global and local tone mapping (Reinhard
et al., 2005). Global tone mapping techniques utilize
a single, and typically highly nonlinear, spatially in-
variant mapping function. In many cases the nonlin-
ear functions are combinations of logarithmic and/or
exponential operators (Reinhard et al., 2002; Drago
et al., 2003; Reinhard, 2011). Global TMOs tend to
preserve the subjective perception of the scene and
have the advantage of being simple and fast. How-
ever, global processing may cause a loss of contrast,
which is apparent in the loss of detail visibility (Zhang
and Kamata, 2008). Local TMOs utilize local neigh-
borhood around a pixel in the mapping. This implies
that two different HDR image pixels with the same
intensity can be mapped to different LDR image val-
ues. This can make the local TMOs bring out more
details compared to a global method, but usually at a
cost of longer processing time. However, local meth-
ods may also cause “halo” effects or ringing artifacts
in the resulting LDR image (Reinhard et al., 2002).
The processing time of a TMO is also an issue; sev-
eral of the existing methods are computationally ex-
pensive. Hence, utilizing Graphics Processing Unit
(GPU) (Zhao et al., 2008) or design of hardware ar-
chitecture (Wang et al., 2007) for existing methods
are of interest unless the TMO method used can run
at acceptable times on a single CPU.
In this paper, new global TMOs are proposed uti-
lizing the nonlinear Successive Mean Quantization
Transform (SMQT) (Nilsson et al., 2005b; Nilsson
61
Nilsson M..
SMQT-based Tone Mapping Operators for High Dynamic Range Images.
DOI: 10.5220/0004228700610068
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 61-68
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2005a). To the best of the author knowledge no
prior tone mapping operation of high dynamic range
images based on the SMQT has been proposed or in-
vestigated. The paper will show that the SMQT is
a good choice for mapping HDR images to LDR. In
particular, it will be shown that the method is fast,
and gives reasonable visual results comparable to the
state-of-the-art.
Two versions of the tone mapping operations are
considered here, one working on luminance and one
version working directly on all RGB channels. The
framework of the luminance approach is in line with
other works (but they do not use or propose the use of
the SMQT). The presented all channel approach is to
the best of the author knowledge novel. It should be
emphasized that, in order to get a general framework,
the derivation, experiments and processing speeds are
conducted using numbers in double precision describ-
ing the HDR image. Hence, if RGB histograms of
the HDR image is available, the processing described
could be performed on those histograms and lead to
further speed improvements.
The paper is organized as follows. In the next sec-
tion formal description of the SMQT is revisited. Sec-
tion 3 presents how the SMQT TMO works on lumi-
nance values as well as the all channel RGB image
and makes a comparison. In section 4 the processing
speed is investigated and a comparison to other state-
of-the-art TMOs is performed. Finally, conclusions
are presented.
2 DESCRIPTION OF THE SMQT
In general, a data point x in a set D consisting of
|D| = D data points are the input to the transform.
The value of a data point is denoted by V(x). Note
that the data structure can be arbitrary, that is D can
be a vector, a matrix or some arbitrary form. In this
paper, the set D is a HDR image of size D = M × N
if gray-scale (luminance) and D = M × N × 3 if color.
The SMQT has only one parameter input: the
level L (indirectly, it will also have the number of data
points D as an important input). The output set from
the transform is denoted M . It has the same form as
the input, that is D could be a color HDR image of
size M × N × 3 then M is also a color image of size
M × N × 3 but with different range of values. The
transform of level L from D to M is denoted
SMQT
L
: D → M . (1)
The SMQT
L
function can be described by a binary
tree where the vertices are Mean Quantization Units
(MQUs). A MQU consists of three steps: a mean cal-
culation, a quantization and a split of the input set.
The first step of the MQU finds the mean of the
data, denoted V, according to
V =
1
|D|
∑
x∈D
V(x). (2)
The second step uses the mean to quantize the values
of data points into {0, 1}. A comparison function is
defined as
ξ
V(x),
V
=
1, if V(x) >
V
0, else.
(3)
If
N
denotes concatenation, then
U =
O
x∈D
ξ
V(x),
V
(4)
is the mean quantized set. The set U is the main out-
put from a MQU. The third step splits the input set
into two subsets:
D
0
= {x | V(x) ≤
V,∀x ∈ D}
D
1
= {x | V(x) >
V,∀x ∈ D},
(5)
where D
0
propagates the left and D
1
propagates the
right of the binary tree, see Fig. 1.
MQU
D
MQU MQU
MQU
D
0
D
1
U
MQU
MQU MQUMQU MQU
Figure 1: The operation of one Mean Quantization Unit
(MQU).
The output set U from a MQU is not a value or a
similarity coefficient as in the linear transforms. In-
stead, U can be interpreted as the structure of D.
Hence, the MQU is independent of the gain and bias
adjustments of the input.
The MQU constitutes the main computing unit for
the SMQT. The first level transform, SMQT
1
, is based
on the output from a single MQU, where U is the
output set at the root node. The outputs in the bi-
nary tree need extended notation. The output set from
one MQU in the tree is denoted U
(l,n)
, where l =
1,2,...,L is the current level, and n = 1,2,...,2
(l−1)
is the output number for the MQU at levell, see Fig. 2.
Weighting of the values of the data points in the
U
(l,n)
sets is performed and the final SMQT
L
is found
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
62

MQU
MQU MQU
MQU
MQU MQU
MQU
MQU MQU
MQU
MQU MQU
MQU
MQU MQU
MQU
MQU MQU
MQU
MQU MQU
MQU
Level 1: 2
L−1
Level 2: 2
L−2
Level 1: 2
L−1
Level 3: 2
L−3
Level 2: 2
L−2
.
.
.
Level 3: 2
L−3
U
(1,1)
MQU
U
(2,1)
MQU
U
(2,2)
MQU
U
(3,1)
MQU
U
(3,2)
MQU
U
(3,3)
MQU
U
(3,4)
MQU
Figure 2: The Successive Mean Quantization Transform
(SMQT) as a binary tree of Mean Quantization Units
(MQUs).
by adding the results. The weighting is performed by
2
L−l
at each level l. Hence, the result for the SMQT
L
can be found in the following way
M = {x | V(x) =
∑
L
l=1
∑
2
l−1
n=1
V
u
(l,n)
· 2
L−l
,
∀x ∈ D, ∀u
(l,n)
∈ U
(l,n)
}.
(6)
As a consequence of this weighing, the number of
quantization levels, denoted by Q
L
, for a structure of
level L will be Q
L
= 2
L
. Since the main aim here is to
produce low dynamic range images the most natural
choice is L = 8.
3 SMQT-BASED TONE MAPPING
OPERATIONS
Most color imaging systems today use a single image
sensor and a Color Filter Array (CFA) to capture full
color images. A color filter array enables each pixel
to capture the intensity of light with different color
spectrum. The most common design of CFA is the
GRGB Bayer pattern (Bayer, 1976) which consists of
two greens, one red, and one blue component. A CFA
image is then interpolated via a demosaicing algo-
rithm and produces a final RGB color image. Hence,
in most cases color image are initially in RGB format
from which the proposed TMOs are derived.
Let a RGB HDR image be denoted I
HDR
(i, j, k)
where i = 0,1,...,M − 1 is the row index, j =
0,1,...,N − 1 the column index and k = 0,1,2 the
color channels red, green and blue. Addition-
ally, let R
HDR
(i, j) = I
HDR
(i, j, 0),∀i, j, G
HDR
(i, j) =
I
HDR
(i, j, 1),∀i, j and B
HDR
(i, j) = I
HDR
(i, j, 2),∀i, j
be the RGB matrices for the HDR image. Same nota-
tions will follow for a LDR image, but with subscript
LDR. To simplify notation, the indices i, j and k are
dropped unless specifically required.
In general, a TMO can be seen as a 3-D matrix
mapping
I
LDR
= f(I
HDR
) (7)
where f(•) is the general tone mapping. One ap-
proach commonly adopted for tone mapping is to con-
vert the RGB to luminance, L
HDR
, as
L
HDR
= 0.299R
HDR
+ 0.587G
HDR
+ 0.114B
HDR
(8)
and perform a mapping L
LDR
= g(L
HDR
) on the lumi-
nance only. To find the LDR color channels, the desat-
urated color-to-luminanceratios can be used (Schlick,
1994; Mantiuk et al., 2009)
R
LDR
=
R
HDR
L
HDR
s
L
LDR
G
LDR
=
B
HDR
L
HDR
s
L
LDR
B
LDR
=
G
HDR
L
HDR
s
L
LDR
(9)
where s controls color saturation. Other techniques
may be employed in order to correct the color result
(Mantiuk et al., 2009). Note that TMO utilizing the
mapping g(·) rely on luminance only, implying color
space conversion and that color information is later
adjusted to achieve the final result.
Given an HDR image in red, green and blue for-
mat, I
RGB
, a TMO aims at finding a good balance
between image features, contrast and color fidelity.
The SMQT has been shown to have desirable proper-
ties in achieving a balanced contrast enhancement for
LDR gray-scale images (Nilsson et al., 2005b; Nils-
son et al., 2005a). Note that the SMQT can be seen as
a nonlinear compression of data points with a higher
number of bits to a defined new, and lower, quan-
tization level L set by the user. Hence, the SMQT
can be used directly on gray-scale HDR images and
one possibility for HDR tone mapping is to apply it
in luminance space, see Fig. 3. However, a different
I
HDR
I
LDR
I
γ
HDR
Eq. (8)
L
HDR
SMQT
L
(·) Eq. (9)
Figure 3: HDR to LDR image using the SMQT on lumi-
nance channel as a tone mapping operator.
approach is also proposed here, the full RGB image
(all channels) will be used to find a mapping func-
tion h(·) using the SMQT which then is employed
on the channels independently as R
LDR
= h(R
HDR
),
G
LDR
= h(G
HDR
) and B
LDR
= h(B
HDR
). Thus, no
color space transformation needs to be employed (if
given an image already in RGB), see Fig. 4.
SMQT-basedToneMappingOperatorsforHighDynamicRangeImages
63

(a) Tone mapping result by SMQT on luminance. (b) Tone mapping result by SMQT over all RGB channels.
Figure 5: Comparison between luminance SMQT TMO, processing as in Fig. 3, and all RGB channel SMQT TMO, processing
as in Fig. 4. The parameters used are L = 8, γ = 1/2.2 and s = 0.8.
I
HDR
I
LDR
I
γ
HDR
SM QT
L
(·)
Figure 4: HDR to LDR image using the SMQT on all RGB
channels as a tone mapping operator.
An exemplified comparison between the lumi-
nance version and all channel RGB SMQT-based
TMO can be found in Fig. 5, to the right of each image
the log-luminance of the HDR intensity is plotted ver-
sus the mapped intensity of the LDR image for each
color channel. Note that a property following from
the SMQT applied on all channel RGB, as well as the
luminance mapping according to Eq. 9, is that the or-
der of intensity values in R, G and B for a pixel will
be the same in input and output since the channels use
the same monotone mapping, see Fig. 5.
4 EXPERIMENTAL RESULTS
The proposed luminance SMQT and all channel RGB
SMQT based TMO are implemented in Matlab
R
,
with parts of the SMQT operation rewritten in ANSI
C and wrapped to a mex file in order to gain speed.
The processing speed for the processing chains found
in Fig. 3 and Fig. 4 (note that it includes gamma cor-
rection) for HDR images of various size can be found
in Fig.6. The processing speed between the lumi-
nance and all channel RGB method are very similar,
but the all channel RGB is somewhat faster. This im-
plies that SMQT on M×N×3 data points is similar to
SMQT on M × N data points with additional color to
luminance found in Eq. 8 and producing color output
found in Eq. 9. Hence, if the SMQT processing speed
can be reduced the all channel RGB TMO is expected
0 1 2 3 4 5 6 7 8
0
2
4
6
8
10
12
14
16
18
20
22
HDR image size in megapixels
FPS
720p, FPS: ~4.1
1080p, FPS: ~1.9
640 × 480, FPS: ~11.9
5MP, FPS: ~0.8
all channel RGB SMQT, L=8
luminance channel SMQT, L=8
Figure 6: FPS for different sizes of HDR images. Circles
with text indicate FPS for the SMQT-based all channel RGB
TMO.
to increase its FPS more compared to the luminance
version. For a timing comparison with other work,
Mantiuk et al. implemented a TMO in Matlab and re-
ported a processing speed of 1.7 seconds (0.59 FPS)
on 2.6GHz CPU for a 1M-pixel image (Mantiuk et al.,
2008). The proposed luminance SMQT-based TMO
achieves 3.60 FPS and the all channel RGB SMQT-
based TMO 3.80 FPS on a 2.13GHz CPU for a 1M-
pixel image. However, GPU and hardware architec-
ture solutions of TMOs naturally report higher frame
rates (Zhao et al., 2008; Wang et al., 2007). A vi-
sual comparison to other state-of-the-art TMOs can
be found in Fig. 7. The SMQT-based methods use the
parameters L = 8, γ = 1/2.2 and s = 0.8 and the other
TMOs use the default parameters defined in the Lu-
minance HDR software
1
. Note that the SMQT-based
TMOs, similar to other state-of-the-art TMOs, pro-
duce naturally looking LDR images.
1
Luminance HDR version 2.2.1 from http://
tpfsgui.sourceforge.net/
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
64

A B
C
D E F
(a) HDR image Stanford memorial church.
A B
C
D E F
(b) HDR image Nancy church 2 from MPI.
A B
C
D E F
(c) HDR image Iwate from MPI.
A B
C
D E F
(d) HDR image Garage from RIT MCSL High Dynamic Range Image
Database.
A B
C
D E F
(e) HDR image Racecar from RIT MCSL High Dynamic Range Image
Database.
A B
C
D E F
(f) HDR image Snow from MPI.
A B
C
D E F
(g) HDR image MPI Atrium 1 from MPI.
Figure 7: Tone mapped HDR images. TMO by (A) Reinhard et al. (Reinhard et al., 2002), (B) Durand and Dorsey (Durand
and Dorsey, 2002), (C) Drago et al. (Drago et al., 2003), (D) Mantiuk et al. (Mantiuk et al., 2008), (E) the proposed
luminance channel SMQT-based method and (F) the proposed all channel RGB SMQT-based method. Zooming in the pdf
images is recommended for detail studies.
SMQT-basedToneMappingOperatorsforHighDynamicRangeImages
65

L = 1 2
3
4
5 6
7
8
Figure 9: Example of image quality on Stanford memorial for different levels L. Top is SMQT-based all channel RGB tone
mapping operation. Bottom is SMQT-based luminance channel tone mapping operation.
1 2 3 4 5 6 7 8
3
4
5
6
7
8
9
10
L
FPS
all channel RGB SMQT
luminance channel SMQT
Figure 8: Processing speeds on a one megapixel image in
Frames Per Second (FPS) on a 2.13GHz CPU. The param-
eters used are γ = 1/2.2 and s = 0.8.
4.1 Improving Processing Speed
While the processing speed for the proposed SMQT
TMOs are some of the fastest reported on a single
CPU, with regard to implementation on embedded
systems, it is still desirable to achieve better process-
ing speeds. The choice of the level used so far is
L = 8, simply due to the fact that the aim is eight
bit images. However, selecting a level L lower can
be a direct way to reduce processing speed but with
reduced image quality. Note that the final output is
still desired to be eight bits and selecting L as a lower
number results in L bit output. Hence, a direct way to
again produce a eight bit result from any selected L is
to multiply the result from Fig. 3 or Fig. 4 with 2
8−L
resulting in an eight bit image
I
8 bit LDR
= I
LDR
· 2
8−L
. (10)
As mentioned, it is expected that the all channel
RGB will benefit more than the luminance version in
a reduction of the SMQT processing speed, see Fig. 8.
The all channel RGB method benefits more from the
reduction in processing speed of the SMQT, for ex-
ample at L = 5 the speed is more than 30% higher
in FPS compared to the luminance method on a one
megapixel image.
Naturally, the image quality decreases as the level
is decreased, see Fig. 9. A subjective observation
from the resulting images constructed with different
levels is that around L = 4 and L = 5 acceptable re-
sults can be achieved. In order to objectify this state-
ment the Peak Signal to Noise Ratio (PSNR) is cal-
culated for the luminance of images and as reference
the eight bit image is used. The seven images found
in Fig. 7 are used and the mean PSNR is calculated,
see Fig.11(a). Selecting a threshold at 30 dB, which
has been found to be suitable from a psychophysical
viewpoint (F. Xiao, 2005), coincide with choosing a
level around four for both methods. Additionally, the
quality mapped to mean opinion scores, Q
MOS
, from
HDR-VDP-2 (Mantiuk et al., 2011) is investigated.
The settings for Q
MOS
calculation are color encoding
selected as sRGB-display and pixels-per-degreeas 30.
The seven images found in Fig. 7 are used and the
mean Q
MOS
is calculated, see Fig.11(b). Note that
around L = 5 the Q
MOS
starts dropping and PSNR
drops below 30 db at around L = 4, hence this coin-
cides well with the initial subjective statement from
observing Stanford memorial, see Fig. 9. Further-
more, the all channel RGB SMQT keeps Q
MOS
higher
compared to luminance channel SMQT at L < 5.
Hence, a reasonable conclusion from this analysis is
that using L = 5 could be a fair choice in order to
reduce computation speed while retaining decent im-
age quality. A comparison of processing speed using
L = 5 can be found in Fig. 10.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
66
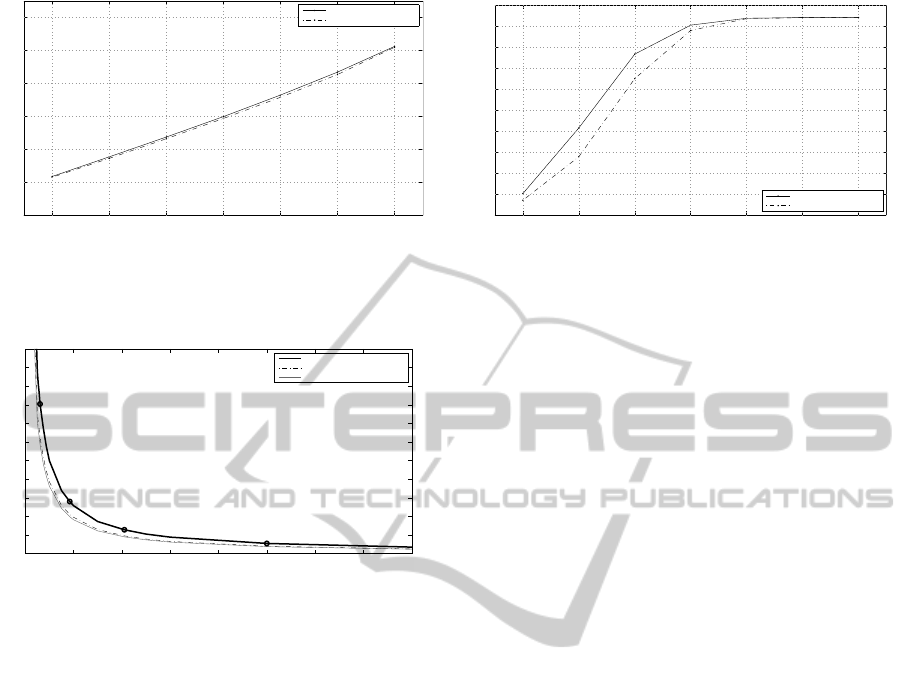
1 2 3 4 5 6 7
0
10
20
30
40
50
60
L
PSNR [dB]
all channel RGB SMQT
luminance channel SMQT
(a) PSNR for different levels using level eight as reference.
1 2 3 4 5 6 7
0
10
20
30
40
50
60
70
80
90
100
L
Q
MOS
all channel RGB SMQT
luminance channel SMQT
(b) Q
MOS
quality measure for different levels using level eight as reference.
Figure 11: Peak Signal to Noise Ration (PSNR) and quality measure (Q
MOS
) for different choices of level L. The parameters
used are γ = 1/2.2 and s = 0.8.
0 1 2 3 4 5 6 7 8
0
2
4
6
8
10
12
14
16
18
20
22
HDR image size in megapixels
FPS
720p, FPS: ~5.6
1080p, FPS: ~2.6
640 × 480, FPS: ~16.1
5MP, FPS: ~1.1
all channel RGB SMQT, L=5
luminance channel SMQT, L=5
reference, L=8
Figure 10: FPS for different sizes of HDR images and L=5.
Reference is average FPS from the two curves found in
Fig. 6. Circles with text indicate FPS for the SMQT-based
all channel RGB TMO.
5 CONCLUSIONS
Two novel global tone mapping operations based on
the nonlinear Successive Mean Quantization trans-
form (SMQT) have been proposed and investigated.
One method is based on applying the SMQT on lu-
minance channel and another is based on performing
the SMQT on all RGB channels. The methods were
compared to other state-of-the-art methods and pro-
duce visually similar results. Regarding the process-
ing speed, they are some of the fastest reported on
a single CPU and can run close to 12 FPS on VGA
(640 × 480) with a 2.13 GHz computer in default
operation. The methods were further investigated
and it was demonstrated that the all channel RGB
has more desirable properties compared to the lumi-
nance method considering processing speed reduction
and associated image degradation. It is found, using
PSNR and Q
MOS
, that a reasonable image degradation
which allows speedup can be achievedat the choice of
level L = 5 in the SMQT. Utilizing L = 5 compared
to the default operation, the all channel RGB method
can run at around 16 FPS while the luminance chan-
nel method achieves 12.5 FPS, on a VGA size image
and a 2.13 GHz computer.
REFERENCES
Bandoh, Y., Qiu, G., Okuda, M., Daly, S., Aach, T., and Au,
O. (2010). Recent advances in high dynamic range
imaging technology. In IEEE International Confer-
ence on Image Processing (ICIP), pages 3125 –3128.
Barakat, N., Hone, A., and Darcie, T. (2008). Minimal-
bracketing sets for high-dynamic-range image cap-
ture. IEEE Transactions on Image Processing,
17(10):1864 –1875.
Bayer, B. E. (1976). Color imaging array. Rochester, NY:
Eastman Kodak Company, U.S. Patent 3 971 065.
Chen, H.-T., Liu, T.-L., and Chang, T.-L. (2005). Tone re-
production: a perspective from luminance-driven per-
ceptual grouping. In IEEE Conference on Computer
Vision and Pattern Recognition (CVPR), volume 2,
pages 369 – 376 vol. 2.
Drago, F., Myszkowski, K., Annen, T., and Chiba, N.
(2003). Adaptive logarithmic mapping for display-
ing high contrast scenes. Computer Graphics Forum,
22:419–426.
Duan, J. and Qiu, G. (2004). Fast tone mapping for high
dynamic range images. In International Conference
on Pattern Recognition (ICPR), volume 2, pages 847
– 850 Vol.2.
Durand, F. and Dorsey, J. (2002). Fast bilateral filtering
for the display of high-dynamic-range images. ACM
Trans. Graph., 21:257–266.
F. Xiao, J. E. Farrell, B. W. (2005). Psychophysical thresh-
olds and digital camera sensitivity: The thousand pho-
ton limit. In Proceedings of the SPIE, volume 5678,
pages 75–84.
Kuang, J., Yamaguchi, H., Liu, C., Johnson, G. M., and
Fairchild, M. D. (2007). Evaluating hdr rendering al-
gorithms. ACM Trans. Appl. Percept., 4.
Lee, J. W., Park, R.-H., and Chang, S. (2010). Tone map-
ping using color correction function and image de-
composition in high dynamic range imaging. IEEE
Transactions on Consumer Electronics, 56(4):2772 –
2780.
SMQT-basedToneMappingOperatorsforHighDynamicRangeImages
67

Liu, C. H., Au, O., Cheng, C. H., and Yip, K. Y. (2010).
Two-level optimized tone mapping for high dynamic
range images. In IEEE International Conference on
Image Processing (ICIP), pages 3153 –3156.
Lu, P.-Y., Huang, T.-H., Wu, M.-S., Cheng, Y.-T., and
Chuang, Y.-Y. (2009). High dynamic range image re-
construction from hand-held cameras. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 509 –516.
Mantiuk, R., Daly, S., and Kerofsky, L. (2008). Dis-
play adaptive tone mapping. ACM Trans. Graph.,
27(68):68:1–68:10.
Mantiuk, R., Kim, K. J., Rempel, A. G., and Heidrich, W.
(2011). Hdr-vdp-2: a calibrated visual metric for vis-
ibility and quality predictions in all luminance condi-
tions. ACM Trans. Graph., 30(4):40.
Mantiuk, R., Mantiuk, R., Tomaszewska, A. M., and Hei-
drich, W. (2009). Color correction for tone mapping.
Comput. Graph. Forum, 28(2):193–202.
Meylan, L. and Susstrunk, S. (2006). High dynamic range
image rendering with a retinex-based adaptive filter.
IEEE Transactions on Image Processing, 15(9):2820
–2830.
Nilsson, M., Dahl, M., and Claesson, I. (2005a). Gray-scale
image enhancement using the SMQT. In IEEE Inter-
national Conference on Image Processing (ICIP), vol-
ume 1, pages 933–936.
Nilsson, M., Dahl, M., and Claesson, I. (2005b). The suc-
cessive mean quantization transform. In IEEE Inter-
national Conference on Acoustics, Speech, and Signal
Processing (ICASSP), volume 4, pages 429–432.
Pattanaik, S. N., Tumblin, J., Yee, H., and Greenberg, D. P.
(2000). Time-dependent visual adaptation for fast re-
alistic image display. In Proceedings of the 27th an-
nual conference on Computer graphics and interac-
tive techniques, SIGGRAPH, pages 47–54.
Qiu, G., Mei, Y., Lam, K. M., and Qiu, M. (2010). Tone
mapping hdr images using optimization: A general
framework. In IEEE International Conference on Im-
age Processing (ICIP), pages 3129 –3132.
Reinhard, E. (2011). Tone reproduction and color appear-
ance modeling: Two sides of the same coin? In 19th
Color and Imaging Conference.
Reinhard, E. and Devlin, K. (2005). Dynamic range re-
duction inspired by photoreceptor physiology. IEEE
Transactions on Visualization and Computer Graph-
ics, 11(1):13–24.
Reinhard, E., Stark, M., Shirley, P., and Ferwerda, J. (2002).
Photographic tone reproduction for digital images.
ACM Transactions on Graphics, 21(3):267–276.
Reinhard, E., Ward, G., Pattanaik, S., and Debevec, P.
(2005). High Dynamic Range Imaging: Acquisition,
Display, and Image-Based Lighting. Morgan Kauf-
mann Publishers Inc., San Francisco, CA, USA.
Schlick, C. (1994). Quantization techniques for visualiza-
tion of high dynamic range pictures. In Photorealistic
Rendering Techniques, pages 7–20. Springer-Verlag.
Wang, T.-H., Wong, W.-S., Chen, F.-C., and Chiu, C.-
T. (2007). Design and implementation of a real-
time global tone mapping processor for high dynamic
range video. In IEEE International Conference on Im-
age Processing (ICIP), volume 6, pages VI –209 –VI
–212.
Zhang, J. and Kamata, S.-i. (2008). Adaptive local contrast
enhancement for the visualization of high dynamic
range images. In International Conference on Pattern
Recognition (ICPR), pages 1 –4.
Zhao, H., Jin, X., and Shen, J. (2008). Real-time tone map-
ping for high-resolution hdr images. In International
Conference on Cyberworlds, pages 256 –262.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
68
